高超声速边界层转捩研究现状与趋势
0 引 言
层流到湍流的过渡被称为转捩。大量的工程实践表明,转捩是高超声速飞行器的共性基础问题。转捩引起边界层流态的显著变化,进而显著影响飞行器局部或整体的气动力/热,而气动力/热是飞行控制、热防护系统设计等的输入,因此,边界层转捩研究结果会显著影响飞行器相关分系统的设计。恩格斯曾说“科学从系于技术的状况和需要”,高超声速边界层转捩研究不外如是,它从系于当前高超声速飞行器快速发展需要。但是,由于扰动形式的多样性、扰动与平均流之间、扰动与扰动之间相互作用的多样性和非线性使得转捩成为一个非常复杂的科学问题,至今未得到很好解决,并且,随着新型飞行器的研制,出现了更多更具挑战性的问题。
本文通过对高超声速边界层转捩研究现状的概述来试图预判转捩研究的发展趋势,主要包括:高超声速飞行器主要发展阶段与遇到的转捩问题[1]、边界层转捩机理研究主要进展[2]、边界层转捩预测方法现状[3]、边界层转捩试验方法现状[4]四个部分。相关综述文献还有很多,不一一例举,最近的一篇是文献[5],本文从这些文献中受益良多。
1 高超声速飞行器主要发展阶段与遇到的转捩问题
1.1 高超声速飞行器主要发展阶段
高超声速概念可追溯至1928年,由德国人Sänger提出。1946年,钱学森与冯·卡门进一步发展和推广了这一概念。随后,人们先后用火箭(1949年,马赫数达到6.7)、返回舱(1961年,马赫数最高达到25)、飞机(1961年,X-15试验飞机,马赫数达到5.3)等形式实践了这一概念。由于湍流加热远大于层流,因此,在高超声速飞行器的发展过程中,转捩与湍流一直是气动领域最大的困扰。
高超声速飞行器的发展脉络如图1所示,这些飞行器均遇到了显著的转捩和湍流问题。
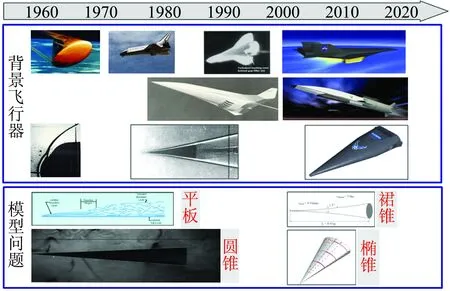
图1 高超声速飞行器发展脉络与主要模型Fig.1 Development and main models of hypersonic vehicles
20世纪50年代中期,人们在以X-15飞机探索高超声速技术时,就已经发现边界层转捩后湍流能够引起涂层烧蚀,局部结构破坏,初步揭示了边界层转捩和湍流在高超声速飞行中的重要性和可能带来的棘手问题[1]。
20世纪60~70年代,人们围绕平板和圆锥(含钝锥)两类边界层开展了转捩和湍流研究[7-11],重点攻克了再入飞行器、航天飞机中由于转捩和湍流引起的烧蚀问题,以及弹头小型化中由于小迎角下非对称转捩引起的飞行不稳定问题。
20世纪80~90年代,美国提出了NASP计划,高超声速边界层转捩和湍流的研究重心也随之转入面对称高升阻比外形,并持续至Hyper-X计划[12],重点解决超燃冲压发动机进气道起动问题,研究了多类人工转捩技术和湍流效应。
2003年哥伦比亚号航天飞机失事后,事故调查再次给出警示,如欲提高进入任何大气的能力,必需重视飞行器各种流态问题。使得此后的十多年里,高超声速飞行器上的转捩和湍流问题得到了前所未有的重视,不仅开展大量的地面研究,而且开展非常具有针对性的专门用于转捩问题的飞行试验,如HyBoLT项目[13]、HIFiRE项目[14-17]。
1.2 当前高超声速飞行器中的转捩问题
高超声速技术被视为一种颠覆性技术,是当前研究热点。目前,高超声速飞行器按气动外形和飞行方式可分为大钝头弹道再入飞行器、细长体滑翔再入飞行器、类航天飞机、吸气式高超声速巡航飞行器,这些飞行器在一个较宽的速域和空域范围内飞行,都存在转捩和湍流问题。
大钝头弹道再入飞行器如返回舱、火星登陆飞行器、深空探测返回飞行器。它在外形上具有非常大的半锥角,在顶点和边缘处钝化。其中主要的转捩和湍流问题有[1]:在钝体迎风面存在烧蚀引起的边界层转捩;在背风面尾迹流动中存在混合层转捩。此类飞行器通常在迎角状态下飞行,轴对称条件被破坏,转捩预测变得更加困难。
细长体滑翔再入飞行器如美国FALCON HTV系列飞行器。它在外形上的主要特征是后掠升力面,其中主要的转捩和湍流问题有[1]:后掠前缘上由横流失稳引起转捩;在中心线附近存在T-S波引起的转捩;在钝化头部的下游还存在熵吞等效应;在长时间飞行过程中表面出现明显的粗糙度,引起瞬态增长形式的转捩。
类航天飞机如X-37B,这是一种小型化航天飞机。相比于航天飞机,由于尺寸减小,转捩和湍流问题减弱。美国通过航天飞机30年的飞行实践积攒了大量经验数据,包括转捩和湍流数据,但我国缺少这些数据。其上主要的转捩和湍流问题有[18]:缝隙、鼓包、表面质量引射等引起的边界层转捩。
吸气式高超声速巡航飞行器如X-43A与X-51A。它在外形上前体采用乘波设计,前缘锐化。主要的转捩和湍流问题有[19]:多级压缩或曲面压缩进气道上的转捩;进气道唇口和稳定段存在严重的激波-边界层干扰流动;燃烧室中需要利用湍流实现混合增强;尾喷管处同样存在湍流问题。
这四类飞行器是高超声速技术的未来发展方向,可以预见,在未来10~20年内,转捩研究仍将围绕这四类飞行器开展工作。
1.3 需要关注的三类模型
基于这些飞行器外形和弹道特点,除平板和圆锥外,有三类模型在未来高超声速边界层转捩中会变得更加重要。
第一类模型是HIFiRE-1锥-柱-裙外形[14]。相对于平板或圆锥,它通过柱-裙段引入了激波-边界层干扰问题,可以用来研究流向行波失稳与分离流共同引发的转捩现象。这种转捩现象普遍存在于飞行器压缩面、翼和控制舵附近,很难预测准确。

图2 HIFiRE-1模型上的边界层转捩现象[15]Fig.2 Boundary layer transition on HIFiRE-1 model[15]
第二类模型是HIFiRE-5椭锥外形[16]。相对于平板或圆锥,它在迎角0°时就存在较强的横流效应,且这种横流效应不同于小迎角下圆锥的横流效应,是所有三维飞行器上普遍存在的现象[20]。如图3所示,椭锥上的转捩同时受第二模扰动、驻定横流模态和行进横流模态的共同作用,目前对这一转捩过程的认识不是特别清楚,因此很难预测准确。
第三类模型是裙-锥外形。该模型的背景为曲面压缩进气道,主要用于认识Görtler涡与Mack模态的相互作用[21-22]。1997年,Doggett和Chokani[23]在NASA Langley的马赫数6静风洞中研究了NASA 93-10裙锥模型上的转捩;2010年,Chou和Schneider等[24-25]在普渡大学的静风洞里试验研究了该模型的稳定性和转捩问题,采用温敏漆技术给出了图4所示的“热-冷-热”条带结构。
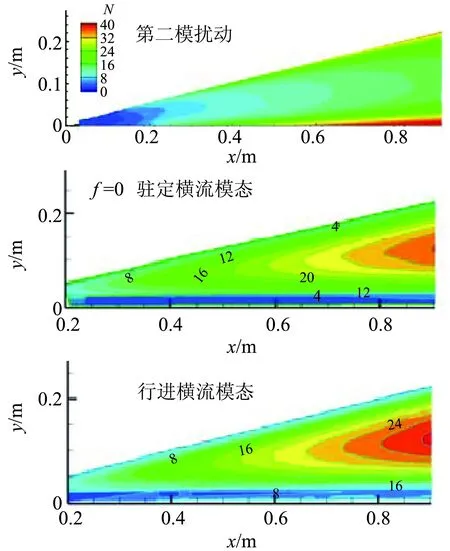
图3 HIFiRE-5模型上的三类扰动模态[17]Fig.3 Three-type disturbance wave mode on HIFiRE-5 model[17]

图4 裙锥模型温敏漆试验照片[25]Fig.4 Temperature sensitive paint image on flared-cone model[25]
上述三类模型在外形上仍是简单模型,但是在转捩机制上却不同于平板和圆锥问题,体现了转捩研究的进步。相比于圆锥,HIFiRE-1多了柱-裙段,使得可以研究流动分离对转捩的影响;HIFiRE-5中变为1∶2椭锥,使得横流效应成为一个重要机制;裙锥中锥面具有曲率,从而引入了Görtler涡对Mack模态扰动的影响。这些都是一些新的前沿的转捩问题。同时,这三个模型问题抓住了工程中转捩相关问题的物理实质,因此,能够更好的衔接学术研究与工程技术需求。
2 边界层转捩机理研究主要进展
2.1 边界层自然转捩理论研究的历史脉络
首先简单回顾一下边界层转捩理论方面的研究进展。自1883年O.Reynolds的圆管流动试验证实流动存在层流和湍流两种不同流态后到今天的130多年里,人们对转捩问题进行了持续不懈的努力,以期解释湍流的成因,期间取得了许多显著的进展。理论方面的主要进展如图5所示[2,26],更详细论述可参阅文献[2]。
在小扰动条件下,目前的研究指出,边界层转捩存在四类失稳机制,分别是:流向行波不稳定性、横流不稳定性、Görtler不稳定性与附着线不稳定性。

图5 边界层转捩机理研究的主要进展Fig.5 Evolvement of mechanisms study onboundary layer transition
2.2 流向行波失稳转捩
流向行波不稳定性是指由Tollmein-Schlichting扰动波(简称T-S扰动波)引起的流动失稳。该类扰动根据扰动波相速度与主流速度的相对关系,又分为亚声速和超声速扰动。对于绝热可压缩平板边界层流动,Mack研究指出[29],当来流马赫数大于2.2时出现第二模扰动,当来流马赫数超过4之后,第二模扰动将成为最不稳定扰动波。但在边界层外缘马赫数小于7时,第一模扰动仍对转捩有重要影响,重要程度取决于壁面冷却的程度和物面形状。第二模及其以上扰动统称为Mack模态,它具有很高的频率。1997年,Wilkinson[4]在NASA兰利中心马赫数6静风洞对裙锥边界层进行了稳定性测量,试验给出,主导的第二模扰动频率测量值约226 kHz,分析结果为230 kHz,这些扰动存在具有非线性行为的谐波分量,谐波峰值频率为449 kHz和670 kHz。
诸多因素都能影响这类不稳定性,并进而影响到转捩。首先是壁温条件,高超声速边界层中一个重要的现象是冷却壁面对第二模扰动具有不稳定效应[2,36-37],这与低速边界层中壁面冷却的稳定效应相反。2016年,我们[38]通过eN方法研究了壁温这个单一因素对转捩位置的影响,结果如图6所示,对于马赫数6,单位来流雷诺数5.81×106/m的平板边界层,在壁温小于1200 K时,壁温越高,转捩越靠后;壁温超过1200 K以后,变化趋势发生了反转。高超声速长时间飞行时,壁温会达到一个较高值,与地面模拟条件存在显著差异,这是转捩天地相关性研究必须考虑的重要因素。
其次是总温,1986年,Mack研究了总温对边界层稳定性的影响[39]。1999年,Kimmel和Poggie[40]用实验展示了增加总温对流动的稳定效应,对来流马赫数8的冷却壁面尖锥,改变风洞驻点温度,使Tw/T0保持常数,结果表明,当总温T0增加24%时转捩位置推迟10%。
头部或前缘钝度对流动稳定性也有较大影响,存在“反转”现象。Stetson通过试验指出[41-43],对于圆锥外形,中等大小的头部钝度推迟了高超声速边界层的转捩;当钝度大于某一临界水平时,头部钝度又提前了转捩,尤其是对于强冷却壁面,如图7所示。但是,这种反转现象在理论分析和计算中一直未得到复现,因此并不清楚其机制。2010年,Lei和Zhong采用线性稳定性理论研究了上述反转现象,研究了0.156、0.5和1.5 inch三个头部钝度,根据结果,他们认为,这种反转现象很可能是风洞试验中某些不可控的噪声产生了有限幅值扰动所引起的,它超出了线性稳定性范畴,同时如果计算仅引入小幅值扰动时需要更长的计算域,因此建议数值模拟非线性有限幅值扰动的演化来揭示这种反转机制。2011年,Kara等[44]数值研究了钝度对高超声速5°圆锥边界层感受性和稳定性的影响,头部钝度rn=0.001~0.1inch,计算也未发现反转现象。同样,小的前缘钝度在平板和空心圆柱流动中也能推迟转捩[45]。

图6 平板边界层转捩位置随壁温的变化(Ma=6)[38]Fig.6 The rules of transition location towall temperature(Ma=6)[38]
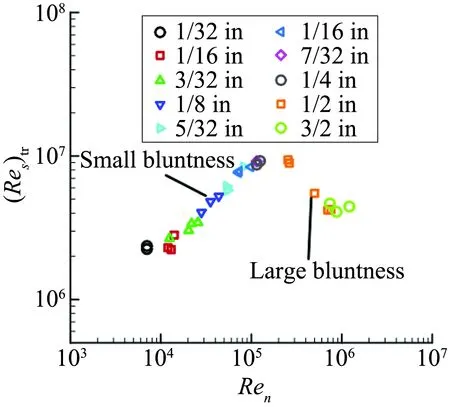
图7 圆锥头部钝度对边界层转捩雷诺数的影响(Ma=5.5)[41]Fig.7 Transition Reynolds number vs.Reynolds numberbased on nose radius(Ma=5.5)[41]
横向曲率同样影响流动稳定性。1991年,Spall和Malik[46]用线性稳定性方法研究了马赫数5的绝热圆锥、圆柱和平板边界层流动,发现横向曲率对三维第一模扰动(倾斜扰动或非轴对称扰动)有不稳定效果,而对二维的第一模和第二模扰动具有稳定效果,影响最显著的地方是头部附近。因此,当流动稳定性由三维第一模扰动主导时,平面外形有利于推迟转捩;而当流动稳定性由第二模扰动主导时(对于高马赫数流动与冷却壁面),需要开展线性稳定性分析来确定横向曲率对流动稳定性影响的净效应。
此外,顺压梯度对边界层具有稳定效应[37,47],顺压梯度能够稳定第二模扰动,逆压梯度对第二模扰动具有不稳定效果,将促进转捩。
2.3 横流失稳转捩
在三维飞行器中,横流不稳定性将非常显著地影响边界层转捩。当边界层存在展向压力梯度时,很容易出现横流涡,它是扁平的同向旋转的涡,可能是驻定的,也可能是行进的。横流涡的最主要作用是将边界层内部的流向低动量流体转移至展向。改变部件外形以减小横流是控制横流转捩的最实用方法,它最主要的问题来自飞行器气动外形的约束条件,而其它横流转捩的控制方法效果都非常有限。2012年以前的工作可参见文献[48]。最近几年的工作主要围绕HIFiRE-5开展,包括静风洞和稳定性分析工作[49-53]。
2011年,Borg等[49]试验研究了HIFiRE-5飞行器表面的附着线和横流失稳机制。研究发现来流的状态直接影响着横流失稳机制。当来流为静音状态时,可以观察到同时存在横流驻波和横流行波,而在噪声条件下,两种波动都未观察到。作者还研究了粗糙单元对附着线失稳的影响,结果表明,粗糙单元的临界高度受来流影响显著,对于静音来流,不同形状的粗糙单元的临界高度之上提高30%(相对于噪声条件),因此,基于噪声风洞设计的粗糙单元尺寸过于保守,不会对飞行器表面的自然转捩产生影响。2014年,Chynoweth等[51]对马赫数6静风洞(BAM6QT)中圆锥边界层转捩和不稳定扰动波进行了试验研究。采用温敏漆和PCB压力传感器成功捕捉到了Mack模态扰动波及其非线性破碎过程。在小迎角状态时,发现在静音和噪声来流条件下都存在横流行波,头部的粗糙单元对锥身上驻定涡的产生具有重要影响。上述波的结构和特征与相应的计算结果非常接近。试验中在横流驻波破碎的地方探测到了高频扰动,但当传感器转动一个小角度时,扰动消失了,表明这种不稳定性与横流驻波的二次失稳有关。2015年,Borg等[52]继续对HIFiRE-5表面的横流行波进行了试验研究,采用压力传感器对不稳定波进行了测量,通过分析三个压力传感器的交叉谱,计算得到了横流波的相速度和波角,与稳定性分析的结果非常吻合。横流行波在静音条件下表现出很弱的非线性相互作用,作者推测这不是主导的转捩机制。2016年,Borg和Kimmel[53]采用红外成像技术首次在静风洞中观测到了HIFiRE-5上的横流驻波,如图8所示。压力传感器的测量结果也表明了横流行波的存在。驻波和行波的波长与之前试验的结果吻合。在噪声条件下,在转捩区之前未发现横流驻波和行波,因此在噪声条件下主导的转捩机制仍不清楚。2016年,Lakebrink和Borg[20]对横流失稳现象开展了抛物化稳定性分析,并与静风洞结果进行了比较,分析结果与试验结果在来流雷诺数小于8.3×106/m时符合很好,但在(8.3~9.8)×106/m时分析结果与试验结果的偏离程度随雷诺数的增加而变大。
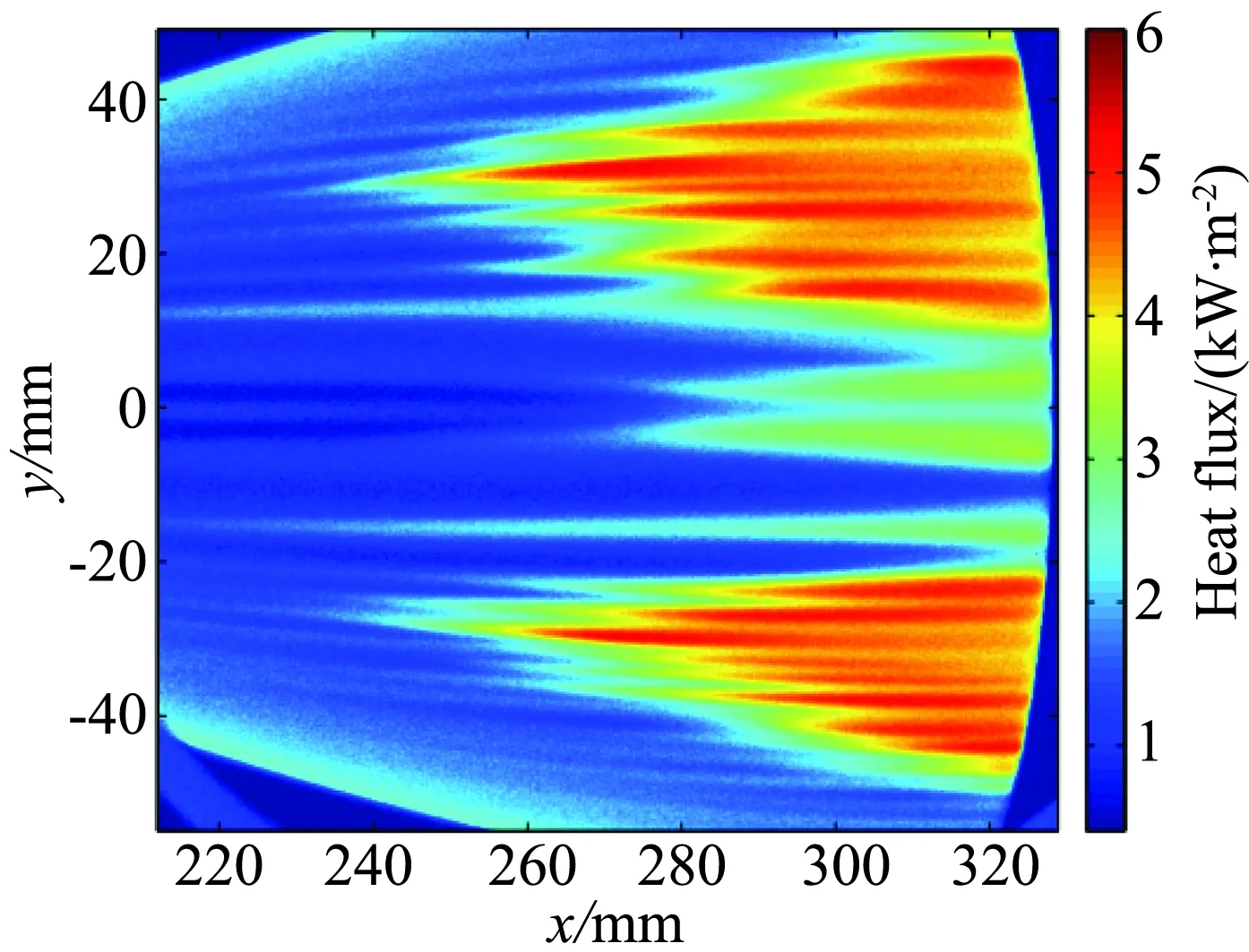
图8 HIFiRE-5上的驻定横流涡(Re=12.3×106/m,Ma=6)[53]Fig.8 Stationary crossflow vortices on HIFiRE-5 model (Re=12.3×106/m,Ma=6)[53]
2.4 Görtler涡失稳转捩
Görtler不稳定性源于物面曲率,对于高超声速发动机进气道的压缩面和尾喷管上的流动转捩有重要影响。由于离心效应,Görtler不稳定性形成驻定的、反向旋转的涡。Görtler不稳定性的控制主要是减小表面曲率及减小Görtler数。
在高超声速边界层中,边界层附近的温度调整层使得流动又有了一些新的特征,不仅存在不可压中的传统的W模态(涡模态扰动集中在壁面附近),还存在着T模态(扰动不在壁面附近而是在边界层外缘附近)。当马赫数大于4时,模态T是最不稳定的。在高雷诺数时,模态T会与传统的模态W相交,Dando和Seddougui使用渐进理论,Ren和Fu[54]使用PSE方法研究了这两种模态增长率之间的交互。在高超声速边界层中,很难靠Görtler涡的自身失稳引发转捩,但是Görtler涡这种定常的旋转流向涡在流场中能产生并促进低速高速条带,而条带的二次失稳通常被认为是导致转捩的关键因素,因此在可压缩曲面边界层中,Görtler涡的研究更多的集中在其二次失稳方面。Li等[55]研究了马赫数6的凹面流动,发现奇模态相比偶模态更为危险,同时温度扰动大于速度扰动,如图9所示。

图9 三种Görtler涡失稳模态的典型特征函数[55]Fig.9 Representative eigenfunctions ofthree Görtler instability mode[55]
2015年,Ren和Fu[56]对高速下Görtler涡的二次失稳进行了较为系统的研究,研究的马赫数范围为Ma=0.015~6,Görtler涡的发展促进了边界层条纹结构,在向下游演化中条带幅值保持增长。除了二次失稳转捩路径,Li等还研究了 Görtler与Mack模态之间相互作用导致转捩的路径。2016年,Sivasubramanian和Fasel[21]对裙锥模型上的转捩进行了直接数值模拟,Kuehl和Paredes[22]一起采用稳定性理论研究了裙锥模型上Görtler涡对Mack模态扰动的影响。
2.5 附着线失稳转捩
对于三维外形,很难明确给出附着线的定义,仅对一些简单外形,如轴对称体或无限大平板,能够给出附着线的定义,此时,附着线一般定义为该曲线上静压最大。而更直观的,附着线代表了一类特殊的流线,它将流动分为两支,一支绕上表面流动,另一支绕下表面流动,如图10所示。附着线失稳相关研究可见文献[57-58]。
对于附着线,由于其特殊位置,附着线的流动状态很大程度上决定了翼面或飞行器表面上的流动状态。附着线附近的扰动可以沿着边界层向展向传播,因此存在一个临界雷诺数,在此雷诺数之上,扰动增长,进而会形成湍流状态的附着线,使下游的飞行器表面都变成湍流。而在此雷诺数之下,扰动衰减,附着线边界层保持层流状态,对下游流动的状态不产生决定性的影响。
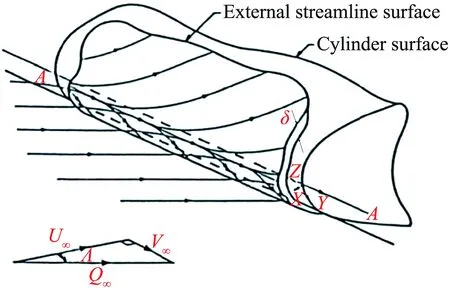
图10 后掠翼绕流的附着线[57]Fig.10 Flow around swept wing attachment line[57]
附着线上流动如何自然转捩,以及在附着线上和不在附着线上施加人工转捩的效果如何,都有待进一步深入研究。
从边界层转捩机理研究的现状可以看到,认识在持续深入,但还是有很多问题需要深入研究。未来自然转捩的机理研究将集中在:发展三维曲面的PSE稳定性分析方法,用DNS研究扰动的非线性演化以及扰动之间的非线性作用,认识横流失稳现象和附着线失稳现象,以及Mack模态扰动与横流扰动、Görtler扰动之间的相互作用。
3 边界层转捩预测方法现状
边界层转捩预测方法包括eN、转捩判据工程预测方法、转捩模型预测方法、大涡模拟和直接数值模拟方法。
3.1 eN方法现状
20世纪50年代中期,Smith和Gamberoni,以及Van Ingen研究了线性稳定性理论预测的扰动增长信息以及从高品质低速风洞中获得的转捩试验数据之间的关系,各自独立地发展出了eN方法,用于转捩预测。这种半经验半理论性质的方法至今仍是工程领域中应用最为广泛的转捩预测方法。近年,为满足高超声速边界层稳定性和转捩分析的要求,美国专门发展了STABL软件,其主要的趋势是用PSE代替LST[59-60],并考虑化学非平衡影响。Bedke认为,用PSE代替LST,eN方法对转捩的预测精度具有质的提高。针对试验中未能考虑的一些影响因素,如头部烧蚀、迎角和飞行器弹体热变形等因素,同样可以用PSE-Chem方法来评估这些因素对转捩影响的重要程度。eN方法最主要的问题是,转捩对应的N因子与初始扰动幅值直接相关,当初始扰动幅值未知时,也就不能确定N因子。
3.2 转捩判据工程预测方法现状
转捩判据是从大量地面试验和飞行试验数据总结出的经验关系。历史上,针对各类湍流问题突出的飞行器均研制了相应的转捩判据,例如对平板问题、圆锥问题、钝头外形的再入飞行器、航天飞机等,提出的转捩判据包括Potter & Whitfield转捩判据(1962)、Van Driest-Blumer转捩判据(1967)、PANT转捩判据(1975)、BATT-LEGNER转捩判据、Boudreau转捩判据(1981)、NASA转捩判据(1981)、Reθ/Me判据(1997)、BLT判据、Reda粗糙度转捩判据[61](2007)、Schneider粗糙度转捩判据[62](2007)等。但是,转捩判据依赖于经验数据,因此,这些判据在推广用于新的飞行器外形和新的飞行弹道时准度会明显下降,换言之,对于每一类新的飞行器均须发展专属的转捩判据。
3.3 转捩模型预测方法现状
转捩模型是计算复杂外形转捩的主要方法。它包括间歇因子模型、基于层流脉动能量概念的转捩模型、v2-f转捩模型。
1958年,Dhawan & Narasimha[63]就已经提出间歇因子概念,它定义为在整个转捩阶段流动为湍流所占有的时间分数。其后,1980年Abu-Ghannam[64],1991年Mayle[65]基于这一概念发展转捩模型。最早是经验的代数形式的转捩模型。2000年,Suzen & Huang[66]提出了间歇因子输运方程形式的转捩模型。2005年,Papp等[67]将该模型用于模拟高超声速边界层流动。2008年,Papp等[68]将上述工作拓展到3D计算,模拟了小迎角高超声速圆锥边界层转捩情形。但是,定量结果仍与试验结果存在明显差异。2009年,符松和王亮[69]提出三方程形式的Fu-Wang模型,该模型在超声速平板、圆锥和高超声速圆锥边界层转捩的模拟结果与试验结果定量符合很好。
基于层流脉动能量概念的转捩模型是一类比较新的转捩模型,它基于对边界层预转捩区层流脉动能量的理解。1997年,Mayle和Schulz[70]在建模过程中阐述了流向扰动与通常意义上湍流扰动之间的区别。流向扰动的能量几乎全部包含在流向分量中;它们的动力学性质也不存在由大尺度到小尺度的能量级串过程,相反,扰动增长到哪种尺度由边界层自身决定,并且一直保持相对较低的波数,因而,除近壁区因无滑移条件引起较大耗散外,耗散也相对较小。为此,他们提出用层流脉动动能kL的方程来描述预转捩区该类型扰动的发展过程。2004年,Walters和Leylek[71],以及Laurdeau等[72]给出了该模型的最新公式,采用一方程形式来描述转捩之前的非湍流脉动。该模型已经被用于传统两方程k-ω模型RANS计算中,形成一个三方程模型。2014年,杨金龙等[73]对γ-Reθ模型和层流脉动能量模型进行分析比较,指出,γ-Reθ模型精度依赖于经验公式和近似处理,层流脉动能量模型预测精度依赖于数值试验修正;当湍流度增大时,γ-Reθ模型预测的精度下降,也不能模拟转捩前边界层内非湍流脉动动能的变化,而层流脉动能量模型与实验值较为吻合。该模型在原理上符合物理过程,但是目前除平板边界层和涡轮扇片上的少数应用外,尚未得到广泛的验证,因此不能对模型的品质下结论。但是,从这些初步的应用来看,该模型很有前途,能够对自由来流湍流度做出正确的敏感性响应。
v2-f转捩模型[3]基于这样的认识,对于旁路转捩而言,壁面法向的湍流脉动 在转捩过程中发挥重要作用。已有的一些结果表明,对于小的来流湍流度,该模型给出了较早的转捩位置,而且,低估了u′的峰值。这些结果还指出,f的方程在不同雷诺应力间负责能量分配,因此,尤其是在转捩区域还需进一步校准。
由于转捩模型能够用于更复杂的几何外形,并与现代CFD技术兼容,因此,是转捩预测方法的重要发展方向,主要趋势包括:1) 针对新型飞行器,对现有模型进行重新校准,提高转捩位置和形态的预测精度;2) 根据飞行器转捩特征发展新的模型,模型中包含飞行器最重要的转捩机制;3) 在形式上均采用当地变量,降低模型使用成本。
3.4 基于LES和DNS的转捩预测方法现状
大涡模拟(LES)和直接数值模拟(DNS)方法能够模拟扰动的线性和非线性过程,具有很强的转捩预测能力,其关键是网格、高精度格式和亚格子模型。
对于充分发展湍流而言,大涡模拟要求单个方向的网格数目达到Re1/2,直接数值模拟要求单个方向的网格数目达到Re3/4,其中的Re为积分尺度定义的雷诺数。例如,2009年,Takashi等[74]进行了当时最大规模的DNS计算,对各向同性湍流计算的网格数目达到40963,接近700亿网格。如此巨大的计算量需求限制了LES和DNS在工程中的应用。但是,对于转捩预测而言,由于该过程仍以大尺度结构为主,无需追求过高的空间分辨率,网格数目可以大幅减小。目前缺乏与湍流模拟那样明确的网格数目标准,多数时候以网格收敛作为评价标准。根据经验,我们给出一种简单的网格估算方法。以流动最不稳定波波长为单位1,当网格尺寸能够分辨出比它尺度小1个量级的波(1/10波长)时,计算就能较好的模拟转捩过程,分辨一个波需要3~5个点,假定计算域某个方向的尺度为L,那么,该方向需要的网格数目为30L~50L。结合加密函数、网格自适用和网格守恒律等技术,对网格进行合理分配,网格数量可以进一步减小。
在格式精度上,LES和DNS要求最少达到3阶精度以上。高精度格式具有更高的空间分辨率,可以降低对网格数目的需求,这是它的优势,但是,高精度格式在复杂边界处很难处理,在激波等间断附近很容易不稳定,目前,工程上主要采用的高精度格式是WENO格式[75-76]及其变种[77-79]。模型问题的计算还可采用特征滤波形式的紧致格式[80]。
LES最核心的是亚格子模型,详见文献[81]。目前的亚格子模型均建立在不可压缩流动的认识基础之上。傅德薰等[82]通过DNS证实,在马赫数5以下,内压缩性较小,Morkovin假设基本合适,此时,这些亚格子模型也基本适用,但当马赫数进一步提高,内压缩性继续增强,这些模型将不再适用。
本文对LES和DNS方法仅做简要介绍,原因是目前LES和DNS在工程中应用有限,它在现阶段的主要发展方向是,与稳定性理论相结合,引入理性的外部扰动,通过对模型问题的转捩过程的精细模拟来认识转捩机制[21,83-86];研究人工转捩装置、局部凸起或凹腔等对转捩过程的影响[87-88],以及流动分离与转捩的相互作用[89]。
4 边界层转捩试验方法现状
高超声速边界层转捩试验始于20世纪50年代,在半个多世纪里,人们用试验提供了大量流动稳定性和转捩方面的基础认识,为稳定性理论和数值模拟提供了验证和确认数据。边界层转捩试验同样需遵循相似原理,因此,转捩试验方法的进展实际上是不断提高模拟相似度,未来的发展趋势仍在于此。
4.1 边界层转捩风洞模拟能力现状
表1列出了部分开展过边界层转捩试验的国内外风洞,从中可以大致看到高超声速边界层转捩的试验能力和发展历史。
首先,在来流雷诺数和马赫数方面追求覆盖高超声速飞行器可能转捩的弹道条件。来流雷诺数对边界层转捩具有显著影响,对于平板或圆锥,当来流雷诺数增加1倍时,转捩雷诺数可增加70%,雷诺数模拟也一直是边界层转捩试验的重要相似准则。2010年,Wadhams等[90]回顾了在CUBRC LENS系列风洞中开展的转捩研究,这些风洞的模拟能力覆盖了X-43、X-51、HIFiRE-1、HIFiRE-5等飞行试验的马赫数(速度)和雷诺数(高度)条件,如图11所示。

表1 开展过高超声速边界层转捩试验的部分风洞Table 1 Wind tunnels performed hypersonicboundary layer transition experiments
其次,努力降低风洞背景噪声,提高风洞流场品质。20世纪50年代,Morkovin就已经开展超声速风洞流场干扰源的研究,讨论多种自由来流脉动的产生可能性。风洞流场的来流扰动区分为涡波、声波和熵波,对于高超声速边界层转捩,影响最大的是声波扰动。高超声速风洞中声波扰动包括从洞壁湍流边界层辐射出的马赫波、洞壁不平引起的马赫波,以及从驻室传播的声波扰动,最主要的是第一类。风洞噪声不仅可以影响模型转捩的位置,甚至会改变其“趋势”。例如,线性稳定性理论表明:半锥角5°圆锥的转捩雷诺数是平板的0.7倍,但是噪声条件下的风洞试验数据却显示,圆锥的转捩雷诺数数比平板模型更高。再如,常规超声速风洞的平板边界层转捩雷诺数均在2×106左右,与eN方法获得的转捩雷诺数数相差5倍以上,而NASA兰利中心的马赫数3.5超声速静风洞获得的试验数据则与eN方法获得的转捩雷诺数符合得很好。同样,Casper等[91]的试验表明,相比于静音环境,噪声条件下绊点的转捩位置更早,如图12所示。

图11 LENS系列风洞的速度/高度模拟能力[57,90]Fig.11 Velocity/Altitude conditions in LENS facilities[57,90]
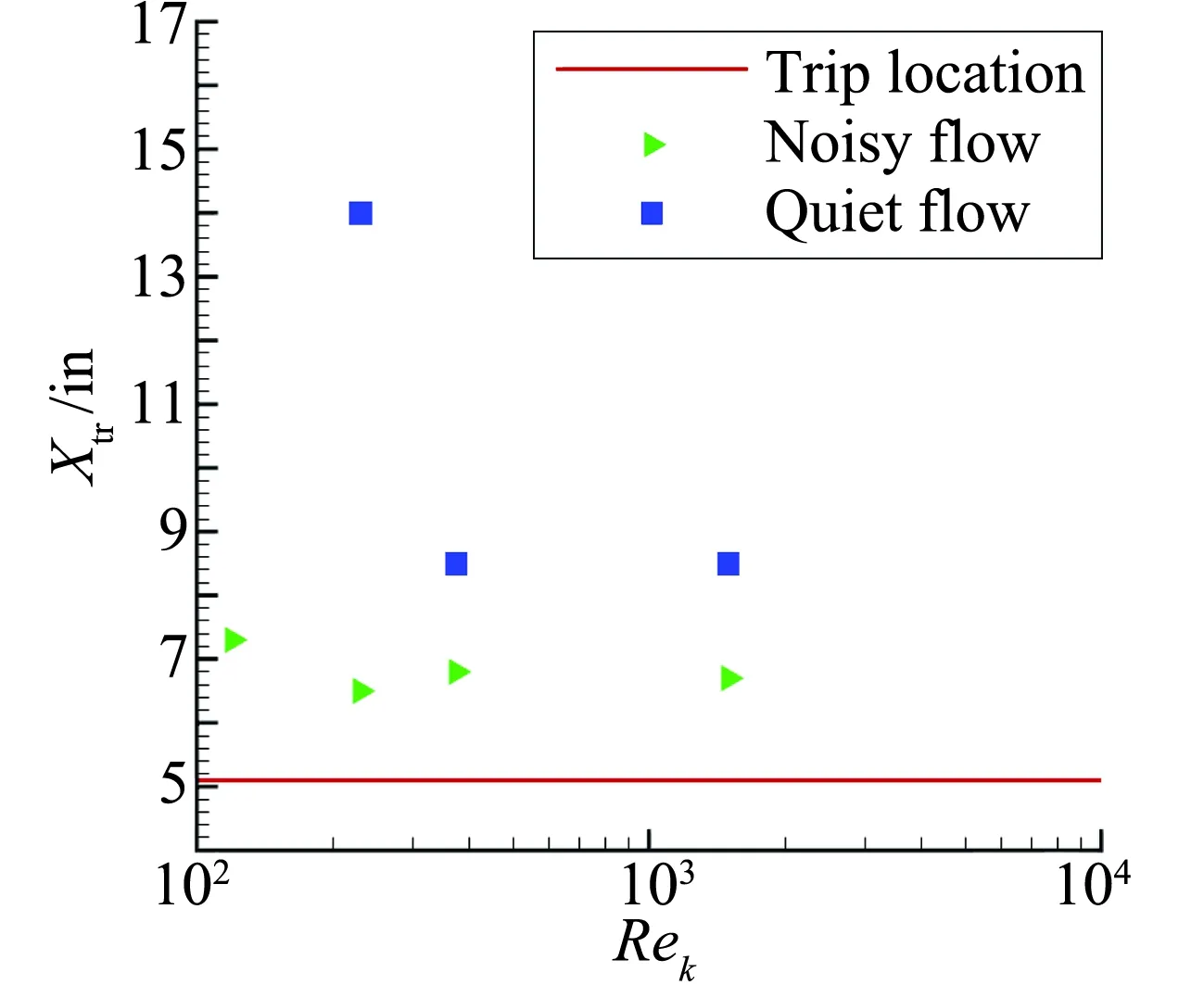
图12 噪声对绊点转捩位置的影响[57,91]Fig.12 Effect of noise on transition location by trip[57,91]
2011年,国内对几座用于转捩研究的风洞进行了背景噪声测量,在马赫数5和6运行条件下,背景噪声均在1%~3%左右。背景噪声对边界层转捩的重要影响使人们从20世纪70年代开始静风洞的设计,1983年,NASA Langley成功建造了世界上首座超声速静风洞,试验马赫数为3.5;1991年又建成了马赫数6的高超声速静风洞,2005年,该风洞搬至Texas A&M大学。目前,在役的高超声速静风洞还有普渡大学的马赫数6静风洞和北京大学的马赫数6静风洞。静风洞的背景噪声降至0.1%~0.01%。
除此之外,总温模拟能力和风洞尺寸也是高超声速边界层转捩的重要能力。例如美国CUBRC的LENS II激波风洞,运行介质可以是氮气或空气,总温最高可达到2500 K,马赫数5~8时喷管直径60 inch(1.524 m),可以开展全尺寸模型的边界层转捩试验,具有很强的复制飞行条件的模拟能力。中科院力学所的JF-12复现风洞喷管直径2.5 m,同样用于全尺寸模型的高超声速边界层转捩研究。
不管怎样,地面风洞模拟环境与实际飞行环境总是存在差异,这种环境的天地差异带来了转捩数据的天地相关性问题,飞行试验是解决该问题的重要环节,也是转捩研究的一个重要方向,但是,本文不对这一问题展开论述。
4.2 边界层转捩测试技术现状
高超声速边界层转捩研究的测试技术很多,基本上是根据层流边界层和湍流边界层不同的物理特征在各方面不同的反映来判断转捩。在20世纪70年代发展了基于气动热测量的边界层转捩测试技术,后又发展了基于壁面剪切应力测量的转捩测试技术。
目前,高超声速边界层转捩试验主要采用热电偶传感器、铂薄膜热电阻传感器、热线技术、脉动压力传感器、ALTP等进行点测量;用磷光热图技术、PLIF、高速纹影、红外热图技术、液晶、温敏漆、压敏漆等进行全局面测量。
热电偶传感器较为常用的包括同轴热电偶和薄壁热电偶,近年来,又发展了新的时域热电偶,热电偶安装在模型表面以下,消除了传感器对表面的破坏作用,提高了测量精度。
薄膜热电阻传感器主要应用于激波风洞和炮风洞,从20世纪50年代开始使用,经过了半个多世纪的研究,目前已经成为超声速和高超声速热流测量最成熟的技术。美国CUBRC使用的铂薄膜热电阻传感器测量精度可以达到±5%。2016年,李素循等[92]将多个薄膜传感器组装成一体,各传感器间距减小到2.5mm,精细测量了光顺平板上的转捩过程,结果如图13所示。

图13 一体式薄膜传感器及平板中心线热流率(Ma=8)[92]Fig.13 Integrated transducers and heat fluxat plate centerline (Ma=8)[92]
热线风速仪[93-94]是低速流动中一种成熟的试验测量技术,根据工作原理的不同,又分为恒温式和恒流式两种。由于高超声速流动的高总压和高总温,热线风速仪在高超声速风洞开始或关闭时常被损坏,但仍被用于高超声速流动的测量。
表面压力传感器[95-96]比热线结实,能够承受较高的动态压力而不被损坏。表面脉动压力传感器对压力分辨率可达7 Pa,响应频率达到1 MHz以上,可以用于测量高超声速边界层失稳、转捩到湍流的脉动信号[97],并判读失稳模态[98-99]和转捩[100]。2015年,Chou和Schneider[101]用14个PCB压力传感器测量了来流噪声引起的扰动,获得了扰动发展的详细数据,部分结果如图14所示。2016年,Chaudhry和Candler[102]研究了自由来流扰动到传感器测量到的压力能谱之间的转换函数。这些工作很可能是未来突破来流扰动或背景噪声测量的关键。
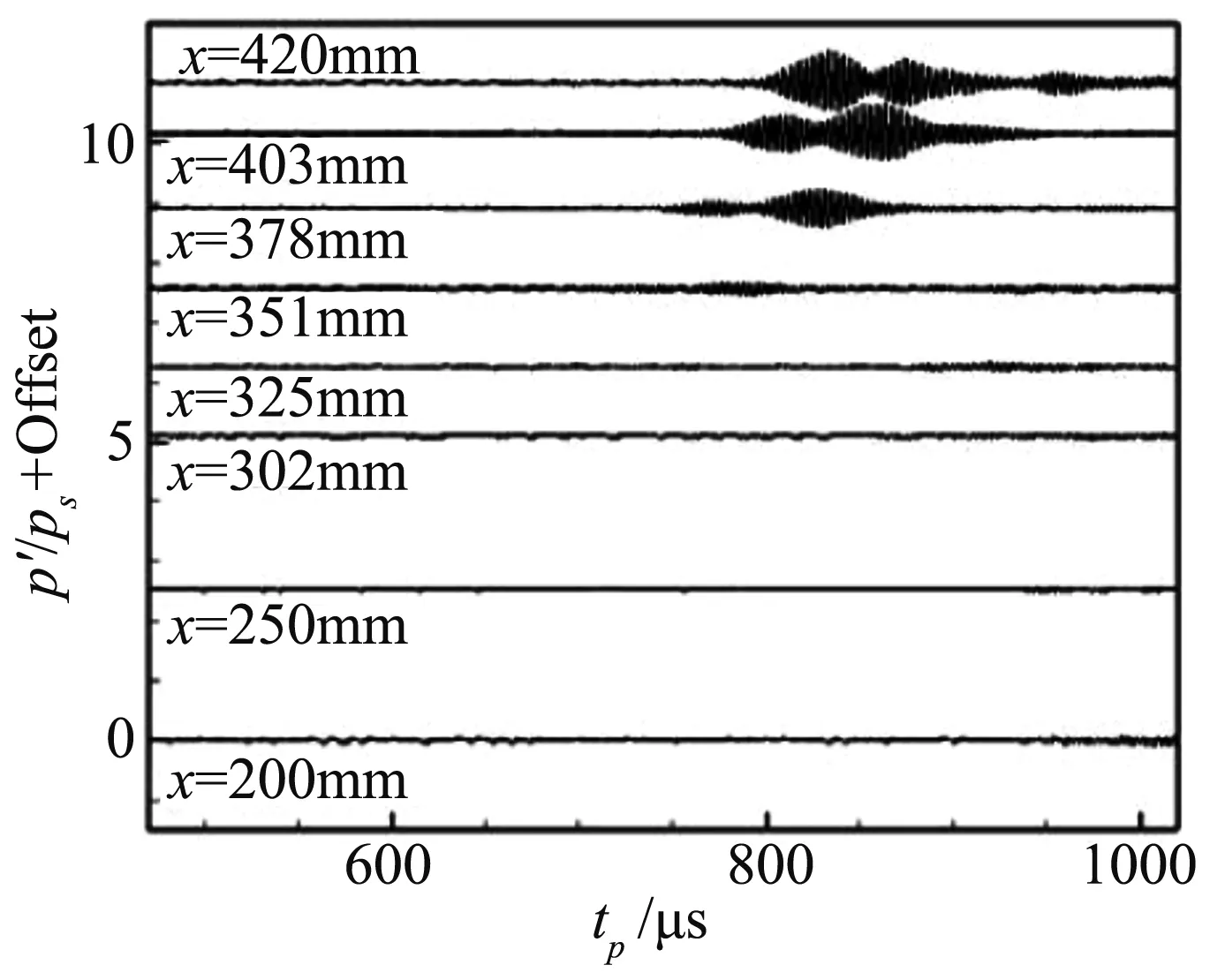
(a) Time series

(b) Power spectral density
ALTP[103-104]是一种较新的热流传感器试验技术。传感器是在SrTiO3或者MgO基座上喷涂分层结构的高度各向异性的YBaCuO薄膜,该薄膜厚度约为500 nm~700 nm。相比于热线风速仪,该传感器能够适应高焓高速、运行时间短的脉冲型风洞,且响应频率要高得多,能够达到1 MHz,可用于第二模扰动及其谐波分量的测量。
NASA Langley中心研发了磷光热图技术,在HIFiRE项目中得到了成功应用。磷光热图技术的不确定性主要是表面温度的变化率。当表面温度显著升高时,如迎风表面大于70 ℉时,测量值的不确定度为±10%。当中等温升时(20~30 ℉),如未发生转捩的前锥尾部,测量值的不确定度为±25%。
另一种值得关注的试验技术是激光诱导荧光技术,这是一种无接触测试技术。2008年,Bathel[105]利用PLIF技术研究了高超声速边界层,试验模型为缩比1∶3的Hyper-X飞行器前体外形,给出了边界层中的层流和湍流结构,并与以前磷光热图技术给出的结果对比,符合很好。2010年,Jiang[106]在马赫数10风洞中开展了PLIF技术的研究,最小曝光时间为10 ns,这些高速照片序列能够给出一系列的层流和湍流流动现象。2010年,Danehy等[107]采用NO PLIF技术在LaRC 31in M10风洞对高超声速平板上不同尺寸圆柱凸起物导致的转捩现象进行了实验研究,实验获得了高超声速边界层上转捩流动结构的尺度、形状和速度。
2009年,Hideyuki[108]利用高速纹影摄像技术研究了高超声速钝锥边界层,显示了边界层中的条纹结构,通过与压力传感器和热电偶等定量测量技术的配合,可以对流场结构有更清晰的认识。
2005年,赵学军等采用红外热成像技术在FD-07风洞中进行了圆锥模型的转捩实验,研究了单位雷诺数对转捩位置的影响。2008年,张骞和艾邦成[109]采用红外热成像技术在电弧加热风洞中进行了尖锥边界层转捩试验研究。2010年,Zhao[110]采用红外热成像技术研究了马赫数5和6高超声速钝锥边界层的转捩位置。2016年,Borg等[53]采用红外热成像技术研究了HIFiRE-5上的转捩现象。
风洞模拟能力和转捩测试技术的进步能够极大地提高人们对于边界层转捩现象的观测能力和机理研究能力,其主要趋势包括:1) 提高静风洞的模拟雷诺数和喷管尺寸;2) 降低常规风洞的背景噪声,改善流场品质;3) 提高传感器的频响和准度,满足二模扰动的测试需求;4) 改进面测量技术的精度和鲁棒性;5) 提高光学测量技术的时空分辨率,实现流动结构的高清显示。另一个重要任务是,开展标模的精细的高超声速边界层转捩实验,为理论分析和数值模拟提供验证与确认数据。
5 建 议
近15年来,边界层转捩和湍流问题在高超声速技术领域得到了更广泛和更深入的研究,本文简要回顾了边界层转捩机理、预测方法和试验能力方面的进展,基于这些现状认识,针对未来高超声速技术对边界层转捩研究的需求提出以下建议:
1) 加强标模转捩研究。标模转捩研究更有利于建立理论研究与工程应用的桥梁,因此,建议针对未来高超声速飞行器设计几类标模,这些标模分别具有对应飞行器上的典型转捩特征,但在外形上应足够简化。
2) 加强多手段综合。工程中转捩问题的复杂性使得任何孤立研究都难以给出确切的认识,因此,应当综合各手段的优势,以合理的研究策略获得对复杂转捩现象的深刻理解。
参考文献:
[1]Reshotko E.Transition issues for atmospheric entry.AIAA 2007-0304[R].Reston: AIAA, 2007.
[2]Kimmel R L.Aspects of hypersonic boundary-layer transition control.AIAA 2003-772[R].Reston: AIAA, 2003.
[3]Pasquale DD, Rona A, Garrett S J.A selective review of CFD transition models.AIAA 2009-3812[R].Reston: AIAA, 2009.
[4]Wilkinson S P.A review of hypersonic boundary layer stability experiments in a quiet Mach 6 wind tunnel.AIAA 1997-1819[R].Reston: AIAA, 1997.
[5]Chen J Q, Tu G H, Zhang Y F, et al.Hypersnonic boundary layer transition: what we know, where shall we go[J].Acta Aerodynamica Sinica, 2017, 35(03): 311-337.(in Chinese)陈坚强, 涂国华, 张毅锋, 等.高超声速边界层转捩研究现状与发展趋势[J].空气动力学学报, 2017, 35(3): 311-337.
[6]Braslow A L.Analysis of boundary-layer transition on X-15-2 research airplane[R].NASA TN-D-3487, 1966.
[7]Pate S R, Schueler C J.Radiated aerodynamic nosie effects on boundary-layer transition in supersonic and hypersonic wind tunnels[J].AIAA Journal, 1969, 7(3): 450-457.
[8]Pate S R.Measurements and correlations of transition Reynolds numbers on sharp slender cones at high speeds[J].AIAA Journal, 1971, 9(6): 1082-1090.
[9]Fischer M C, Wagner R D.Transition and hot-wire measurements in Hypersonic Helium flow[J].AIAA Journal, 1972, 10(10), 1326-1332.
[10]Wagner R D, Maddalon D V, Weinstein L M.Influence of measured freestream disturbances on hypersonic boundary-layer transition[J].AIAA Journal, 1970, 8(9): 1664-1670.
[11]Pate S R.Dominance of radiated aerodynamic noise on boundary-layer transition in supersonic-hypersonic wind tunnels, theory and application[R].AD AEDC-TR-77-107, 1978.
[12]Horvath T J, Berry S A, Merski N R.Hypersonic boundary/shear layer transition for blunt to slender configurations-A NASA langley experimental perspective[R].NASA Report ADA442053, 2006.
[13]Berry S A, Horvath T J.Infrared imaging of boundary layer transition flight experiments.AIAA 2008-4026[R].Reston: AIAA, 2008.
[14]Berger K T, Greene F A.Aerothermodynamic testing and boundary layer trip sizing of the HIFiRE Flight 1 vehicle.AIAA 2008-0640[R].Reston: AIAA, 2008.
[15]Wadhams T P, Mundy E, Maclean M G, et al.Pre-flight ground testing of the full-scale HIFiRE-1 Vehicle at fully duplicated flight conditions: Part II.AIAA 2008-639[R].Reston: AIAA, 2008[16]Juliano T J, Schneider S P.Instability and transition on the HIFiRE-5 in a Mach-6 quiet tunnel.AIAA 2010-5004[R].Reston: AIAA, 2010.
[17]Choudhari M, Chang C L, Jentink T, et al.Transition analysis for the HIFiRE-5 vechicle.AIAA 2009-4056[R].Reston: AIAA, 2009.
[18]Horvath T J, Berry S A, Merski N R, et al.Shuttle damage/repair from the perspective of hypersonic boundary layer transition-experimental results.AIAA 2006-2919[R].Reston: AIAA, 2006.
[19]Middleton T F, Balla R J, Baurle R A, et al.The NASA Langley isolator dynamics research LAB[R].NASA Report 2010-0002214, 2010.
[20]Lakebrink M T, Borg M P.Traveling crossflow wave predictions on the HIFiRE-5 at Mach 6: stability analysis vs.quiet tunnel data.AIAA 2016-0356[R].Reston: AIAA, 2016.
[21]Sivasubramanian J, Fasel H F.Direct numerical simulation of laminar-turbulent transition in a flared cone boundary layer at Mach 6.AIAA 2016-0846[R].Reston: AIAA, 2016.
[22]Kuehl J J, Paredes P.Görtler modified Mack-modes on a hypersonic flared cone.AIAA 2016-0849[R].Reston: AIAA, 2016.
[23]Doggett G P, Chokani N, Wilkinson S P.Hypersonic boundary-layer stability experiments on a flared-cone model at angle of attack in a quiet wind tunnel.AIAA 97-0557[R].Reston: AIAA, 1997.
[24]Chou A.Characterization of laser-generated perturbations and instability measurements on a flared cone[D].West Lafayette, Indiana: Purdue University, 2010.
[25]Berridge D, Chou A, Ward C, et al.Hypersonic boundary-layer transition experiments in a Mach 6 quiet tunnel.AIAA 2010-1061[R].Reston: AIAA, 2010.
[26]Reshotko E.Progress, accomplishments and issues in transition research.AIAA 1997-1815[R].Reston: AIAA, 1997.
[27]Lin C C.The theory of hydrodynamic stability[M].Cambridge university press, 1955.
[28]Lees L, Lin C C.Investigation of the stability of the laminar boundary layer in a compressible fluid[R].NACA Technical Notes 1115, 1946.
[29]Mack L M.Boundary-layer stability theory[R].NASA Report CR-131501, 1969.
[30]Lele S K.Direct numerical simulation of compressible free shear flows.AIAA 1989-0374[R].Reston: AIAA, 1989.
[31]Klebanoff P S, Tidstrom K D, Sargent L M.The three-dimensional nature of boundary layer instability[J].Journal of Fluid Mechanics, 1962, 12: 1-34.
[32]Craik A D D.Non-linear resonant instability in boundary layers[J].Journal of Fluid Mechanics, 1971, 50: 393-413.
[33]Herbert T.Secondary instability of boundary layers[J].Ann.Rev.Fluid Mech, 1988, 20: 487-526.
[34]Herbert T.Parabolized stability equations[J].Ann.Rev.Fluid Mech.1997, 29: 245-283.
[35]Zhou H, Zhao G F.Hydrodynamic stability[M].Beijing: National Defence Industry Press,2004.(in Chinese)周恒, 赵耕夫.流动稳定性[M].北京: 国防工业出版社, 2004.
[36]Stetson K F, Thompson E R, Donaldson J C, et al.Laminar boundary layer stability experiments on a cone at Mach 8, Part 5: Tests with a cooled model[R].AIAA-89-1895, 1989.
[37]Malik M R.Prediction and control of transition in supersonic and hypersonic boundary layers[J].AIAA Journal, 1989, 27(11): 1487-1493.
[38]Liu Z Y, Yang W B, Shen Q.Investigation on correlation between wind tunnel and flight test data for boundary layer transition.AIAA 2016-3980[R].Reston: AIAA, 2016.
[39]Mack L M.Stability of axisymmetric boundary layers on sharp cones at hypersonic Mach numbers.AIAA 1987-1413[R].Reston: AIAA, 1987.
[40]Kimmel R L, Poggie J.Effect of total temperature on boundary layer stability at Mach 6.AIAA 1999-0816[R].Reston: AIAA, 1999.
[41]Stetson K F, Rushton G H.Shock tunnel investigation of boundary-layer transition atM=5.5[J].AIAA Journal, 1967, 5(5): 899-906.
[42]Stetson K F.Nosetip bluntness effects on cone frustum boundary layer transition in hypersonic flow.AIAA 1983-1763[R].Reston: AIAA, 1983.
[43]Stetson K F, Thompson E R, Donaldson J C, et al.Laminar boundary layer stability experiments on a cone at Mach 8, Part 2: blunt cone.AIAA 1984-0006[R].Reston: AIAA, 1984.
[44]Kara K, Balakumar P, Kandil O A.Effects of nose bluntness on hypersonic boundary-lyaer receptivity and stability over cones[J].AIAA Journal, 2011, 49(12), 2593-2605.
[45]Hopkins E J, Jillie D W, Sorensen V L.Charts for estimating boundary-layer transition on flat plates[R].NASA TN-D-5846, 1970.
[46]Spall R E, Malik M R.Effect of transverse curvature on the stability of compressible boundary layers[J].AIAA Journal, 1991, 29(10): 1596-1602.
[47]Zurigat Y H, Nayfeh A H, Masad J A.Effect of pressure gradient on the stability of compressible boundary layers[J].AIAA Journal, 1992, 30(9): 2204-2211.
[48]Xu G L, Fu S.The instability and control of compressible cross flows[J].Advanced in Mechanics, 2012, 42(3): 262-273.徐国亮, 符松.可压缩横流失稳及其控制[J].力学进展, 2012, 42(3): 262-273.
[49]Borg M P, Kimmel R, Stanfield S.HIFiRE-5 attachment-line and crossflow instability in a quiet hypersonic wind tunnel.AIAA 2011-3247[R].Reston: AIAA, 2011.
[50]Borg M P, Kimmel R L, Stanfield S.Traveling crossflow instability for HIFiRE-5 in a quiet hypersonic wind tunnel.AIAA 2013-2737[R].Reston: AIAA, 2013.
[51]Chynoweth B C, Ward C A C, Greenwood R T, et al.Measuring transition and instabilities in a Mach 6 hypersonic quiet wind tunnel.AIAA 2014-2643[R].Reston: AIAA, 2014.
[52]Borg M P, Kimmel R L, Stanfield S.Traveling crossflow instability for theHIFiRE-5 elliptic cone[J].Journal of Spacecraft and Rockets, 2015, 52(3): 664-673.
[53]Borg M P, Kimmel R L.Simultaneous infrared and pressure measurements of crossflow instability modes forHIFiRE-5.AIAA 2016-0354[R].Reston: AIAA, 2016.
[54]Ren J, Fu S.Competition of the multipleGörtler modes in hypersonic boundary layer flows[J].Science China Physics Mechanics and Astronomy, 2014, 57(6): 1178-1193.
[55]Li F, Choudhari M, Chang C L, et al.Development and breakdown of Görtler vortices in high speed boundary layers.AIAA 2010-0705[R].Reston: AIAA, 2010.
[56]Ren J, Fu S.Secondary instabilities of Görtler vortices in high-speed boundary layer flows[J].Journal of Fluid Mechanics, 2015, 781: 388-421.
[57]Reed H L, Saric W S.Attachment-line heating in a compressible flow.AIAA 2011-3242[R].Reston: AIAA, 2011.
[58]Reed H L, Perez E, Kuehl J, et al.Hypersonic stability and transition prediction.AIAA 2013-2556[R].Reston: AIAA, 2013.
[59]Alba C R, Johnson H B, Bartkowicz M D, et al.Boundary layer stability calculations of the HIFiRE Flight 1 vehicle in the LaRC 20-Inch Mach 6 air tunnel.AIAA 2008-0505[R].Reston: AIAA, 2008.
[60]Johnson H B, Candler G V.Analysis of laminar-turbulent transition in hypersonic flight using PSE-Chem.AIAA 2006-3057[R].Reston: AIAA, 2006.
[61]Reda D C, Wilder M C, Bogdanoff D W, et al.Transition experiments on blunt bodies with distributed roughness in hypersonic free flight.AIAA 2007-0306[R].Reston: AIAA, 2007.
[62]Schneider S P.Effects of roughness on hypersonic boundary-layertransitition.AIAA 2007-0305[R].Reston: AIAA, 2007.
[63]Dhawan S, Narasimha R.Some properties of boundary layer during the transition from laminar to turbulent flow motion[J].Journal of Fluid Mechanics, 1958, 3: 418-436.
[64]Abu-Ghannam B J, Shaw R.Natural transition of boundary layers-The effects of turbulence, pressure gradient, and flow history[J].Journal of Mechanical Engineering Science, 1980, 22(5): 213-228.
[65]Mayle R E.The role of laminar-turbulent transition in gas turbine engines[J].Journal of Turbomachinery, 1991, 113: 509-537.
[66]Suzen Y B, Huang P G.Modeling of flow transition using an intermittency transport equation[J].Journal of Fluids Engineering, 2000, 122(2): 273-284.
[67]Papp J L, Kenzakowski D C, Dash S M.Extensions of a rapid engineering approach to modeling hypersonic laminar to turbulent transitional flows.AIAA 2005-0892[R].Reston: AIAA, 2005.
[68]Papp J L, Dash S M.A rapid engineering approach to modeling hypersonic laminar to turbulent transitional flows for 2D and 3D geometries.AIAA 2008-2600[R].Reston: AIAA, 2008.
[69]Fu S, Wang L.Modelling flow transition in a hypersonic boundary layer with Reynolds-averaged Navier-Stokes approach[J].Science in China: Series G, 2009, 39(4):617-626.(in Chinese).符松, 王亮.基于雷诺平均方法的高超音速边界层转捩模拟[J].中国科学G辑, 2009, 39(4): 617-626.
[70]Mayle R E, Schultz A.Path to predicting bypass transition[J].Journal of Turbomachinery, 1997, 119(3): 405-411.
[71]Walters D K, Leylek J H.A new model for boundary-layer transition using a single-point RANS approach[J].Journal of Turbomachinery, 2004, 126(1): 193-202.
[72]Lardeau S, Leschziner M A, Li N.Modelling bypass transition with low-Reynolds-number nonlinear eddy-viscosity closure[J].Journal of Flow, Turbulence and Combustion, 2004, 73(1): 49-76.
[73]Yang J L, Lai H X.Numerical investigation of transitional flow by applying two transitional models for Reynolds average Navier-Stokes simulation[J].Journal of East China University of Science and Technology, 2014, 40(4): 524-532.(in Chinese)杨金龙, 赖焕新.雷诺时均模拟的两种转捩模型比较[J].华东理工大学学报, 2014, 40(4): 524-532.
[74]Takashi I, Toshiyuki G, Yukio K.Study of high-Reynolds number isotropic turbulence by direct numericalsimulation[J].Annu.Rev.Fluid Mech.2009, 41: 165-180.
[75]Jiang G S, Shu C W.Efficient implementation of weighted ENO schemes[J].Journal of Computational Physics, 1996, 126: 202-228.
[76]Balsara D, Shu C W.Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order accuracy[J].Journal of Computational Physics, 2000, 160: 405-452.
[77]Henrick A K, Aslam T D, Powers J M.Mapped weighted essentially non-oscillatory schemes: achieving optimal order near critical points[J].Journal of Computational Physics, 2005, 207: 542-567.
[78]Borges R, Carmona M, Costa B, et al.An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws[J].Journal of Computational Physics, 2008, 227: 3191-3211.
[79]Taylor E M, Wu M, Martin M P.Optimization of nonlinear error for weighted essentially non-oscillatory methods in direct numerical simulations of compressible turbulence[J].Journal of Computational Physics, 2007, 223: 384-397.
[80]Yee H C, Sandham N D, Djomehri M J.Low-dissipative high-order shock-capturing methods using characteristic-based filters[J].Journal of Computational Physics, 1999, 150: 199-238.
[81]Piomelli U.Large-eddy simulation: achievements and challenges[J].Progress in Aerospace Sciences, 1999, 35: 335-362.
[82]傅德薰, 马延文, 李新亮, 等.可压缩湍流直接数值模拟[M].科学出版社, 2010.
[83]Liu J X.Evolution of disturbance in hypersonic blunt cone boundary layer at small angle of attack[D].Tianjin: Tianjin University, 2010.(in Chinese)刘建新.小迎角钝锥高超声速边界层的扰动演化[D].天津: 天津大学, 2010.
[84]黄章峰, 周恒.湍流边界层的空间模式DNS的入口条件[J].中国科学(G 辑: 物理学力学天文学), 2008, 38(3): 310-318.
[85]Dong M, Zhou H.Inflow boundary condition for DNS of turbulent boundary layers on supersonic blunt cones[J].Appl Math Mech-Engl Ed, 2008, 29(8): 985-998.(in Chinese)董明, 周恒.超声速钝锥湍流边界层DNS入口边界条件的研究[J].应用数学和力学, 2008, 29(8): 893-904.
[86]Yu M, Yuan X J, Zhu Z B Assessment of inflow boundary conditions for hypersonic wall bounded turbulent flows[J].Acta Aerodynamica Sinica, 2017, 35(06): 772-776.(in Chinese)禹旻, 袁湘江, 朱志斌.高超声速壁湍流入口条件生成方法的比较[J].空气动力学学报, 2017, 35(6): 772-776[87]Zhao X H, Deng X B, Mao M L, et al.Large eddy simulation for forced transition flow at hypersonic inlet[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2445-2453.(in Chinese)赵晓慧, 邓小兵, 毛枚良, 等.高超声速进气道强制转捩流动的大涡模拟[J].航空学报, 2016, 37(8): 2445-2453.
[88]Dong M.Mechanism of Roughness-induced transition in hypersonic boundary layers[J].Physics of Gases, 2016, 1(5):25-38.(in Chinese)董明.高超声速边界层中由粗糙元引起强制转捩的机理[J].气体物理, 2016, 1(5): 25-38.
[89]Pan H L, Ma H D, Shen Q.LES application to unsteady flat plate shock wave/turbulent boundary layer interaction[J].Acta Aeronautica et Astronautica Sinica, 2010, 32(2): 242-248.
[90]Wadhams T P, MacLean M G, Holden M S, et al.A review of transition studies on full-scale flight vehicles at duplicated flight conditions in the LENS tunnels and comparisons with prediction methods and flight measurement.AIAA 2010-1246[R].Reston: AIAA, 2010.
[91]Casper K M, Wheaton B M, Johnson H B, et al.Effect of freestream noise on roughness-induced transition at Mach 6.AIAA 2008-4291[R].Reston: AIAA, 2008.
[92]Li S X, Shi J, Guo X G.Experimental study of boundary layer features on a flat plate in high speed flow[J].Physics of Gases, 2016,1(6):1-4.(in Chinese)李素循, 师军, 郭孝国.高速流绕平板边界层特性研究[J].气体物理, 2016, 1(6): 1-4.
[93]Rufer S J, Schneider S P.Hot-wire measurements of instability waves on a blunt cone at Mach-6.AIAA 2005-5137[R].Reston: AIAA, 2005.
[94]Rufer S J, Schneirder S P.Hot-wire measurements of instability waves on cones at Mach 6.AIAA 2006-3054[R].Reston: AIAA, 2006.
[95]Alba C R, Casper K M, Beresh S J, et al.Comparison of experimentally measured and computed second-mode disturbances in hypersonic boundary-layers.AIAA 2010-0897[R].Reston: AIAA, 2010.
[96]Casper K M, Beresh S J, Henfling J F, et al.Hypersonic wind-tunnel measurements of boundary-layer pressure fluctuations.AIAA 2009-4054[R].Reston: AIAA, 2009.
[97]Berridge D C, Schneider S P.Calibration of PCB-132 sensors in a shock tube[R].NASA report NF1676L-13491, 2012.
[98]Xie S F, Ji F, Shen Q.Extraction and analysis of the second mode instability wave based on singular-value decomposition and empirical mode decomposition[C]//46th AIAA Fluid Dynamics conference, 2016, Washington, DC, United States.
[99]Ji F, Xie S F, Shen Q.Hypersonic high frequency (1 MHz) fluctuation pressure testing technology and application[J].Acta Aerodynamica Sinica, 2016, 34(5): 587-591.(in Chinese)纪锋, 解少飞, 沈清.高超声速1 MHz高频脉动压力测试技术及其应用[J].空气动力学学报, 2016, 34(5): 587-591.
[100]Wei B B, Gao Y W, Deng L, et al.Transition method in hypersonic boundary based on POD method[J].Physics of Gases, 2016,1(3):25-30.(in Chinese)魏斌斌, 高永卫, 邓磊, 等.基于POD方法的高超声速边界层转捩判定方法[J].气体物理, 2016, 1(3): 25-30.
[101]Chou A, Schneider S P.Boundary layer instabilities generated by freestream laser perturbations[R].NASA report N150005717, 2015.
[102]Chaudhry R S, Candler G V.Recovery of freestream disturbance spectrum from stagnation pressure spectrum for hypersonic pitot probes.AIAA 2016-2059[R].Reston: AIAA, 2016.
[103]Knauss H, Roediger T, Gaisbauer U, et al.A novel sensor for fast heat flux measurements.AIAA 2006-3637[R].Reston: AIAA, 2006.
[104]Maslov A, Boutine D, Shiplyuk A, et al.Experimental study of compressible boundary layer on a cone at angles of attack[J].Acta Mech Sin, 2009, 25: 325-333.
[105]Bathel B F, Danehy P M, Inman J A, et al.PLIF visualization of active control of hypersonic boundary layers using blowing.AIAA 2008-4266[R].Reston: AIAA, 2008.
[106]Jiang N, Webster M, Lempert W R.MHz-Rate NO PLIF imaging in a Mach 10 Hypersonic Wind Tunnel.AIAA 2010-1407[R].Reston: AIAA, 2010.
[107]Danehy P M, Ivey C B, Inman J A, et al.High-speed PLIF imaging of hypersonic transition over discrete cylindrical roughness.AIAA 2010-0703[R].Reston: AIAA, 2010.
[108]Hideyuki T, Tomoyuki K, Kazuo S, et al.Measurement of hypersonic boundary layer transition on cone models in the free-piston shock tunnel HIEST.AIAA 2009-0781[R].Reston: AIAA, 2009.
[109]Zhang Q, Ai B C.Sharp cone boundary layer transition in arc heated flow field[J].Aerospace Materials & Technology, 2008, 5: 25-28.(in Chinese)张骞, 艾邦成.电弧加热流场中的尖锥边界层转捩研究[J].宇航材料工艺, 2008, 5: 25-28.
[110]Zhao X J, Jin X, Shen Q.Experiment researches on the location of transition outset in the hypersonic wind tunnel.AIAA 2010-0674[R].Reston: AIAA, 2010.
———重庆建成世界一流汽车风洞

