基于MAS仿真的保障机构维修保障能力评估指标研究
王 锐,张学峰
(1.海军政治工作部,北京100841;2.91388部队,广东湛江524022)
舰艇编队的使用与维修保障具有与单一装备所不同的诸多特点,例如:在型号上呈多样性,在任务中具有不同地位与作用,在任务目标上具有一致性,在地域空间上具有广阔性,在时间上具有先后性,在任务强度上具有不均匀性,在对各类保障资源的需求上,既具有特殊性又具有共同性等[1-8]。从维修保障资源的角度上看,在舰艇编队中,某些专用于一型舰艇特定装备的保障资源,可能为其他舰艇的某些装备提供保障,在某种程度上,这类原先专用的保障资源具有了通用保障资源的特点[9-12],通过维修保障资源MAS间的协作可以减少保障资源的总数量。
Multi-Agent系统(MAS)是指由多个可计算的Agent组成的集合,其中每个Agent可以是一个物理的或抽象的实体,能作用于自身和环境,并能与其他的Agent通讯[13-14]。MAS也可定义为是由一些对所处环境具有局部观点并可对环境产生局部影响的Agent构成的网络系统[15-16]。Davis[17]给出了定义:MAS是一个分布式系统,系统中多个异步且松耦合的问题求解器共同协作,以完成无法由单一求解器独立承担的任务。在此,异步表明各问题求解器是并行操作的,松耦合表明各问题求解器更多的工作是内部计算,而不是相互间通讯。整个仿真基于蒙特卡罗方法作任意n次实验[18],每次实验首先从数据库中抽样出初始化数据,根据抽样的保障模式来部署这次实验的MAS结构:对码头作业模式,MAS包含想定和评估Agent,装备部Agent,基地级维修Agent,及若干中继级维修分队Agent;对于海上伴随保障模式,MAS包含想定和评估Agent以及若干个舰员级维修Agent。如图1所示。

图1 保障系统的MAS的仿真架构Fig.1 MAS simulation structure of a maintenance supporting system
1 基于MAS的保障机构保障能力指标确定
针对编队的维修保障机构通常采用以下4种作业模式:日常码头保障,出海前集中抢修,海上伴随保障和返航后码头保障。其中,只有海上伴随保障模式需要舰员级维修,且舰员级维修的项目是发生频度较高且难度很小的项目。在其他模式中若遇到发生频度较小且难度很大的项目,则应该由基地级承担,而对于这4种作业模式中的其他维修项目,则由处于中继级地位的编队级修理机构承担。
由于舰员级所担负的维修项目具有突发性,其作用相当急救处理,不需MAS加以优化处理。若舰员在规定的时间内没维修好,则立即转入中继级修理。所以重点针对中继级和基地级的维修项目,采用MAS技术提出最优的保障方案。
从保障的过程来看,它是一个以给定的资源投入、在规定的时间内、使装备保持或恢复到规定的作战效能状态的过程。显然,保障的目标是资源投入少、保障时间短、保障效果好。因此,评估一个保障方案的优劣时,通常从3个方面考虑,即:
1)按保障方案进行保障时,完成保障任务所需的时间;
2)经过保障,装备所能达到的作战效能;
3)保障方案所需的费用。
对舰艇编队维修保障机构而言,其采用的保障方案应当针对一批次的维修项目并基于其所拥有的整个维修力量来设计。
1.1 保障方案所需费用
保障方案所需的费用是该方案各类资源在其寿命周期中的各类费用之和,包括资源的购置费、安装与库存费、使用与维修费等。一个修理机构的修理资源,主要包括人力、设备、设施、技术资料、备品备件、组织与管理等因素。
由于费用数据的固有问题,直接计算保障方案所需的费用可能比较困难,通常可以用“资源的空闲率”或“资源空闲时间”来间接度量费用的高低。最低的“资源空闲率”或“资源空闲时间”说明所配备的资源是最少的,因而应该是最佳的方案。评估修理资源的空闲程度与评估充足程度可同步进行。不仅要按单项资源进行评估,还要对整体情况进行综合评估。对单项资源进行的空闲与充足程度评估可以发现哪类资源不足或过剩的问题;在单项资源评估的基础上,按综合评估模型,对整个维修保障能力进行综合评估,会得到整体的短缺率等指标。
1.2 完成保障任务所需时间
保障任务所需的时间当是自接到整批次的修理工程单开始,到该批次的所有项目都已维修完成为止。保障方案的制定应当根据所拥有的保障资源进行合理的分配,以达到完成保障任务所需时间最短的目的。从完成单项修理任务的时间来看,它包括修理分队的出动时间和实施保障任务所需的时间。
就出动时间而言,灵活、快速、机动是编队级修理力量存在的必要条件和基本要求。修理分队自接到修理工程单开始,到出动修理队伍实施维修之间,有管理环节,也有修理资源和技术的准备(人员、设备、器材、方案与技术资料)环节。实施保障任务所需的时间是指,在对装备实施保障的过程中,由于各类保障资源提供保障时的速度(如零件的加工速度)有限和装备本身的特点(如平均修复时间),决定着保障任务的完成需要一定的时间。
1.3 保障后装备所应具有的效能
维修保障系统的最终目标是保持和提高舰船的在航率、舰艇执行出海训练计划出动及时率、完成任务率、出海训练时间、航行的海里数等,这些都是反映舰船战备完好与任务成功水平的指标,是舰船战斗力的组成部分。根据装备综合保障工程学理论,反映装备保障能力的参数包括保障能力综合参数、有关保障能力设计特性参数和保障系统与保障资源参数。
1)综合参数。保障能力综合参数是从装备战斗力的角度衡量装备保障能力优劣的一些参数,包括战备完好与任务成功及费用相关的参数。如战备完好率、使用可用度、任务可靠度、再次出动时间、寿命周期费用等。
2)有关保障能力的设计特性参数。有关保障能力的设计特性参数是指仅受主装备设计影响的保障性设计特性参数,主要有可靠性、维修性、测试性及运输性等设计特性参数。如平均故障间隔时间、平均维修间隔时间、平均修复时间、故障检测率、故障隔离率、运输重量、运输动态极限参数等。
3)保障系统与保障资源参数。保障系统与保障资源参数都反映保障资源状态对保障能力的影响。前者反映保障系统全体或多项保障资源对保障能力的综合影响,如平均保障延误时间、备件更换维修周转时间、各维修级别故障修复百分数、机动转移时保障资源的运输量等;后者则是单个保障资源要素对保障能力的影响,随资源的种类、消耗与占用特点的不同而有不同指标,例如工具数量与重量、器材库存量、备件满足率与短缺率、保障设备与设施的利用率与空闲率、各类人员的数量与技术等级、各类人力的利用率与空闲率,等等。
2 中继级保障能力评估指标的求解
2.1 修理系统出动能力的指标求解
在正常情况下,中继级修理机构的行政管理延误和交通时间基本保持不变。因此,出动时间的计算主要考虑组建修理分队的时间。
组建修理分队所需的时间可按下述方法统计:如果有N项修理工程、M个能立刻开展修理任务的修理分队,当N>M时,只有前M个工程项目的延误时间为0,第M+1个修理工程的延误时间为并行开展的M个修理项目中完成时间最早的项目的结束时间;同样,第M+2个修理工程的延误时间为第M+1个项目开始后,新的M个修理项目中完成时间最早的项目的结束时间;以此类推。若在N个项目的修理过程中没有新的项目出现,则总的组建修理分队时间(延误时间)为所有N-M个项目延误时间之和。
平均出动时间为一个时期内所有出动时间之和与该时期内所有维修项目数之比,即
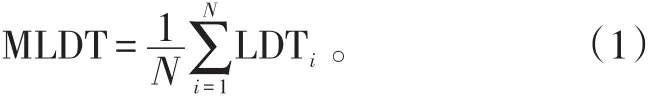
式(1)中:N为该时期内所有维修项目数;LDTi为第i个修理项目的出动时间(即延误时间)。
1)迅速出动率。出动时间小于1 h的次数与该时期内所有维修项目数之比,即
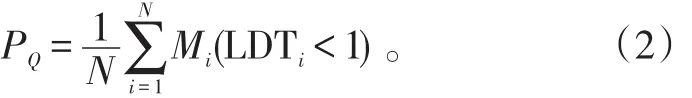
式(2)中:Mi(LDTi<1)为逻辑函数,若 LDTi<1,则Mi=1,反之为0。
2)正常出动率。出动时间小于4 h的次数与该时期内所有维修项目数之比,即

式(3)中:Mi(LDTi<4)为逻辑函数,若 LDTi<4,则Mi=1,反之为0。
2.2 保障效能的评估方法
在海上伴随保障模式下,保障的效能体现在执行任务的等级提升上。提升舰艇任务等级所需的时间是评估保障效能的一种方法,它是舰艇任务能力从第3类提升到第2类、或从第2类提升为第1类所需的时间的平均值。
若在考察的时间段开始时,舰艇处于第3类(或第2类)任务能力状态,并且立刻开始修理,伴随着故障的减少,舰艇的任务能力逐步提升,当舰艇的任务能力由第3类转为第2类(或由第2类转为第1类)时,所经历的时间按下式计算:

式(4)、(5)中:DATE为日期函数;DATE(E=0.5)表示舰艇任务能力到达第3类的日期;DATE(E=0.7)表示舰艇任务能力到达第2类的日期;DATE(E=0.9)表示舰艇任务能力到达第1类的日期。
在返航后码头保障、出海前集中抢修和日常码头保障模式下,保障的效能一方面体现在完成部分修理任务所需时间上;另一方面体现在维修后舰艇技术状态的好坏程度上。从舰艇执行一个特定的任务(例如3 d、7 d、15 d、30 d、60 d、90 d等海上航行任务)返航后,必将产生一批修理项目,针对每一种任务所产生的修理项目,完成其规定比例(如50%、90%、100%)修理任务所需的时间按下式计算。
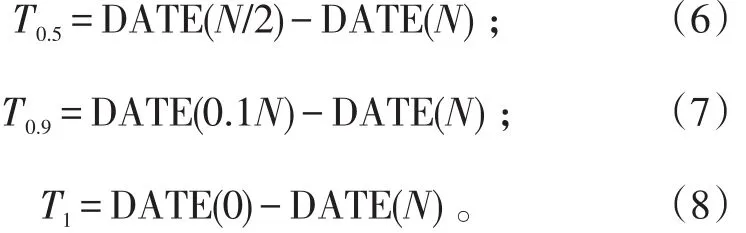
式(6)~(8)中:N为舰艇任务结束时的修理工程总数量;DATE(N)表示返航后开始修理的日期;DATE(N/2)表示修理工程数量完成50%的日期;DATE(0.1N)表示修理工程数量完成90%的日期;DATE(0)表示修理工程数量完成100%的日期。
舰艇技术状态评估方法是以舰艇的故障与维修数据信息为依据,按照舰艇在每一天(或更小的时刻单位,如每一小时等)所存在的故障装备情况,并根据各种不同在航等级(或任务等级)所需的最少设备数量或条令规定的判据,判定舰艇在对应时刻尚可正常工作设备的种类及数量所能满足的在航(任务)等级,如果所判定时刻的可工作设备的种类及数量大于等于一类在航的需要,则对应时刻舰艇的技术状态被判定为一类;如果不能满足一类任务的要求,则判定能否满足二类在航(任务)的需要,如此等等,可以确定出对应时刻舰艇所能达到的技术状态或任务等级(1、2、3类在航状态或任务等级、故障(或检修)停航状态)。对一段时间内的数据进行统计处理的结果可以得到舰艇处于各种状态的天数(或时刻数),经变换,得到舰艇处于不同状态的在航率指标。
为说明前述思路,以图2所示简化的动力装置为例进行分析。当不考虑舰艇其他设备的影响时,对于该动力装置,若4台主锅炉与2台主汽轮机均能够工作,整个舰艇则“能战”,应判为1类在航状态;若只有2台或3台主锅炉能够工作且2台主汽轮机也能够工作,则整个舰艇“能练”,应判为2类在航;若4台主锅炉和2台主汽轮中分别只有1台能够工作,整个舰艇只“能动”而不能“练”和“战”,应判为3类在航状态。
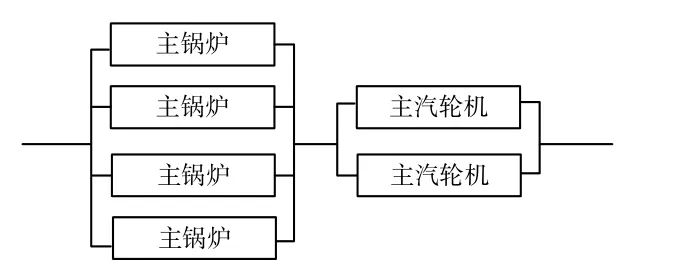
图2 简化的动力装置Fig2 Simplified power equipment
首先,需要给舰艇定义一个指数E,表示其任务能力。例如,E在0.9以上,表示舰艇可执行1类在航状态所对应的任务;在0.7~0.9之间,表示舰艇可执行2类在航状态所对应的任务;在0.5~0.7之间,则表示舰艇可执行3类在航状态所对应的任务;在0.5以下则表示舰艇不能出海执行任务。
第二,判定每一类型的故障对舰艇任务的影响程度Fi,给出分值。影响越严重,分值越高。如果一个故障发生后会使舰艇的技术状态降为3类,则该故障的影响程度应在0.3~0.5之间;如果故障使舰艇的技术状态降为2类,则该故障的影响程度应在0.1~0.3之间;如果故障发生后舰艇的技术状态仍能够保持1类,则该故障的影响程度应小于0.1。上限适用于同类装备数量只有1台的情形。例如,只有1台主汽轮机的舰艇,主汽轮机的故障影响程度应为0.5。下限适用于同类装备数量较多的情形。例如,主汽轮机故障的影响应靠近0.3,主锅炉故障的影响程度应靠近0.1。
第三,累加所有故障的影响程度得到总影响F。E=1-F表示当前舰艇的任务能力。例如,若图2所示动力装置的2台主汽轮机均故障时,舰艇的任务能力指数E=0.4,表示不能出海;而只有1台主汽轮机能工作时,E=0.7,表示仅能执行3类在航状态所对应的任务;若有1台锅炉不能工作,则E=0.9,其技术状态降低为2类。
2.3 保障资源利用率的求解
采用MAS仿真架构后,中继级维修机构在1次仿真中被分割为多个维修分队Agent,这些Agent间通过交互与协作,使每个Agent都能感知到整个保障资源的变化情况。在装备部Agent的协调下,各分队Agent中的人员在一定条件下可重新组织,设备、设施和技术资料可以共享,这显能提高了保障资源的利用率。
从保障资源自身的指标求解来看,大多指标只关心资源是不是被使用,而不关心被谁使用。但针对资源的出动及时率指标的求解,由于Agent间可能重组资源,导致资源的出动及时率受影响,但相对于中继级维修机构完成一批维修作业所花的时长来说,这种影响小到可忽略不计。在此仿真背景下,各保障资源的利用率求解如下。
2.3.1 人力资源评估指标的衡量
1)人员出动及时率。人员出动及时率分为迅速出动率(1 h内出动,在Agent间重组人员时采用此量加以统计)和正常出动率(半个工作日内出动)2个量,用一旦需要这类人员能及时出动的次数与所有修理工作需要这类人员的总次数之比度量。按下式计算:
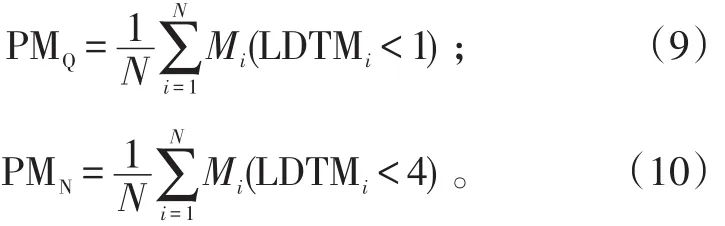
式(9)、(10)中:PMQ为人员迅速出动率;PMN为人员正常出动率;LDTMi为执行第i个修理项目时人员就绪的时间,即LDTMi=datetimeMN-datetimeMI,其中:datetimeMN为这类人员没有另外修理任务、可以执行本修理任务的时刻,该时刻不是修理项目开始的时刻;datetimeMI为第i个修理项目产生或接到执行该修理任务的通知的时刻;Mi(LDTMi<x),x=1,4为逻辑函数,若LDTMi<x则Mi=1,反之为0。
2)平均人员利用率。平均人员利用率是在一个时期内人员利用率的平均值。按下式分不同技术等级和专业类型计算:

式(11)中:PMAU为平均人员利用率,分不同技术等级和专业类型;T为考察时期内的考察时刻数;M为修理单位内该技术等级和专业类型的总人数;Mi为在第i个考察时刻该类技术人员投入工作的数量。
3)平均人员空闲率。平均人员空闲率=1-平均人员利用率。
4)人员工时利用率。按下式分不同技术等级和专业类型计算。该数值可能大于1,表示加班。

式(12)中:PMWTAU为人员工时利用率,分不同技术等级和专业类型;WTi为该时期内第i个修理工程需要该类技术人员投入的工时;N为该时期内该类人员参加的修理工程总数,也可用修理工程总数,对结果无影响。
5)人员工时空闲率。人员工时空闲率=1-人员工时利用率。若该数值为负,则表示加班。
2.3.2 设备资源评估指标的衡量
1)设备投入及时率。设备投入及时率分迅速投入率(1 h内投入,在一Agent需要共享其他Agent的设备时加以统计)和正常投入率(半个工作日内投入),用一旦需要该设备能及时投入的次数与所有修理工作需要该设备的总次数之比度量。按下式分不同型号计算:

式(13)、(14)中:PEQ为设备迅速投入率;PEN为设备正常投入率;LDTEi为执行第i个修理项目时设备就绪的时间,即LDTMi=datetimeEN-datetimeEI,其中:datetimeEN为该类设备中的1台没有另外修理任务、可以执行本修理任务的时刻,该时刻不是修理项目开始的时刻;datetimeEI为第i个修理项目产生或接到执行该修理任务的通知的时刻;Mi(LDTEi<x),x=1,4为逻辑函数,若LDTEi<x,则Mi=1,反之为0。
2)平均设备利用率。平均设备利用率是在一个时期内设备利用率的平均值。按下式分不同型号计算:

式中,PEAU为平均设备利用率,分不同型号。
3)平均设备空闲率。平均设备空闲率=1-平均设备利用率。
4)设备工时利用率。按下式分不同型号计算:

式(16)中:PEWTAU为设备工时利用率,分不同型号;ETi为该时期内第i个修理工程需要该型号设备投入的工时。
5)设备工时空闲率。设备工时空闲率=1-设备工时利用率。
2.3.3 设施资源评估指标的衡量
1)设施使用及时率。设施使用及时率分迅速投入率(1 h内投入,在一Agent需要共享其他Agent的设备时加以统计)和正常投入率(半个工作日内投入),用一旦需要该设施能及时投入的次数与所有修理工作需要该设施的总次数之比度量。按下式分不同类型计算:

式(17)、(18)中:PFQ为设施迅速投入率;PFN为设施正常投入率;LDTFi为执行第i个修理项目时设施就绪的时间,即LDTMi=datetimeFN-datetimeFI,其中:datetimeFN为该类设施中的一座或一部分未被另外修理任务占用、可以执行本修理任务的时刻,该时刻不是修理项目开始的时刻;datetimeFI为第i个修理项目产生或接到执行该修理任务的通知的时刻;Mi(LDTFi<x),x=1,4,为逻辑函数,若 LDTFi<x,则Mi=1,反之为0。
2)平均设施面积利用率。平均设施面积利用率是在一个时期内设施面积利用率的平均值。按下式分不同型号计算:

式中,PFAU为平均设施面积利用率,分不同类型。
3)平均设施面积空闲率。平均设施面积空闲率=1-平均设施面积利用率。
4)设施工时利用率。按下式分不同类型计算。
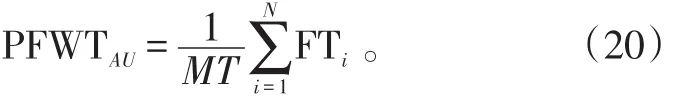
式(20)中:PFWTAU为设施工时利用率,分不同类型;FTi为该时期内第i个修理工程需要该类型的工时。
5)设施工时空闲率:设施工时空闲率=1-设施工时利用率。
2.3.4 备件资源评估指标的衡量
指标1:平均备件延误时间。
1)统计模型。对于一种备件,统计每次需要该备件的维修项目在获取该备件时的延误时间,取其平均值。按下式计算:
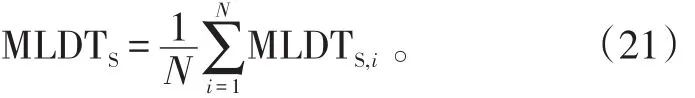
式(21)中:MLDTS为平均备件延误时间,分不同型号;MLDTS,i为修理第i个项目时,获得该备件的时间。
2)预计模型。对于一种备件,可按不同渠道备件满足率及获取时间的加权和预测。按下式计算:

式(22)中:MLDTS为平均备件延误时间,分不同型号;PS,i为第i个供应渠道的备件满足率,MLDTS,i为第i个供应渠道的平均延误时间。
如果仅考虑本级仓库和外部仓库的区分,则按下式计算:

式(23)中:MLDTS为平均备件延误时间,分不同型号;PSL分别为本级仓库备件满足率;MLDTSL为本级仓库的平均延误时间,可取1~4 h;MLDTSE为外筹备件的平均延误时间,可取7~30 d。
指标2:备件满足率。
1)统计模型。在既定的库存管理策略下,一个考察时期内,及时满足某种器材的次数与需要该器材的总次数之比。按下式计算:
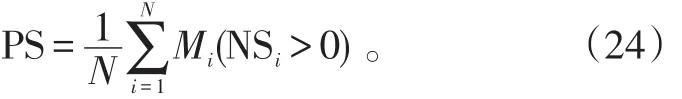
式(24)中:PS为备件满足率,分不同型号;NSi为修理第i个项目时该种器材的库存总量;Mi(NSi>0)为逻辑函数,若NSi<x,则Mi=1,反之为0。
2)预计模型。在既定的库存管理策略和一个供应周期内,备件满足率也就是该周期内的不缺货概率,按下式计算:

式(25)中:X为该供应周期内预期的备件消耗数量;NS为供应周期开始时,该种备件的库存总数,即库存最高限额;P(X≤N)为该供应周期内的不缺货概率;T为供应周期;为该备件的平均故障率,是该备件安装在不同部位时的故障率的平均值;L为整个舰艇编队使用该备件的数量。
3)备件短缺率。备件短缺率=1-备件满足率。
4)库存最高限额。库存最高限额取决于库存管理政策,由维修保障方案给定。
5)平均库存数量。平均库存量有简单平均计算法和期望值计算法2种。
a)简单平均值算法。按下式计算:

式(26)中:NSAV为平均库存数量,分不同型号;NE为该供应周期结束时的库存总数,即最小过剩数量。
b)期望值算法。按下式计算:

式(27)中:NSAV为平均库存数量,分不同型号;NS,i为该备件在第i天的库存总数。
6)最小过剩数量。在一个供应周期结束时的库存量(NE),按实际统计得到。
3 舰员级保障能力评估指标的求解
在舰员级的维修项目中,有很大一部分项目是更换故障件,船上备件是否充足直接影响到保障延误时间。因此,保障资源自给率是舰员级保障能力的一个评估指标。对于舰艇编队的舰员级维修,编队间的备件资源是可以共享的。所以,基于MAS的仿真将每一条舰上的舰员级维修机构当作一个Agent,编队间的所有舰员级Agent就构成了多Agent的群,他们之间通过彼此的通信,能感知到彼此资源的变化,从而提高自身的保障能力。
舰上备件获取平均时间是舰员级保障能力的另一个评估指标。在舰上获取备件时间是指从确定需要某种备件到该备件到达指定的维修地点这段时间,包括行政批准时间、仓库备件寻找时间以及备件从仓库搬运到维修地点的时间;当需要从其他舰获取备件时,还包括运输时间。
保障资源充足率包括维修人员和备品备件,对于一种消耗类资源,例如一个型号的备品备件,其充足率可按下式计算:
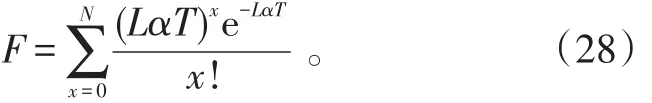
式(28)中:F为保障资源的充足率;L为动力系统中需要该种资源保障的单元总数,例如备件所对应部件在动力系统中的安装总数;α为单位时间内,该资源的消耗速率,例如部件的故障率;T为资源补充间隔时间,例如随舰维修人员修好备件的时间;N为资源在每次补充后的储备数量。
对一种占用型资源,例如一种专业技术等级的人力,其充足率的计算公式来自排队论,可按下式计算:

式(29)~(31)中:n为中间变量,表示蒸汽动力系统同时需要该种保障资源的保障需求(如修理)的数量;F(n)为中间变量,表示动力系统同时存在n个需要该种保障资源的保障需求的概率;F(0)为中间变量,表示动力系统不产生需要该种保障资源的保障需求的概率;c为保障系统中拥有该种保障资源的数量;m为动力系统中会产生需要该种资源保障的潜在保障需求总数;λ为单位时间内,动力系统发生需要该种保障资源的保障需求的概率;τ为每次投入该种保障资源时,资源被占用的平均时间。
保障资源利用率是舰员级保障能力的又一个评估指标,对其求解涉及:该资源的用途(使用该保障资源的保障事件)总数、每种用途所占用的该资源的时间、单位发生使用该保障资源的每个保障事件的发生概率、资源的总数量等因素。
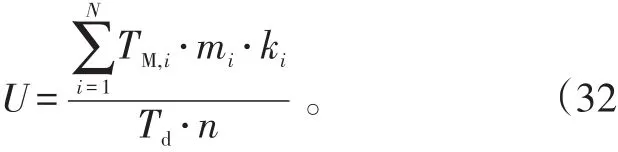
式(32)中:U为一种保障资源的利用率;TM,i为第i个保障项目占用该保障资源的时间;mi为在一段规定的时间内(如1个任务周期内)第i个保障项目发生的次数,取决于装备的工作时间、故障率等消耗性因素;ki为第i个保障项目需要该保障资源投入的个数;Td为在一段规定的时间内(如1个任务周期内)该种保障资源的可工作时间。
4 基地级维修保障能力评估指标的求解
一般采用三级维修作业体制。基地级维修机构承担难度很大的维修项目,这包括一些特型舰艇的维修、新型设备故障的维修等。同时,在采用MAS协同仿真架构后,哪些修理项目须由基地级承担也是“浮动”的,如当装备部发现基地级维修Agent比较空闲时,也可将预分派给中继级的正处于等待的维修项目转给基地级承担,这样可充分利用保障力量的资源,确保了舰艇编队具有高的战备完好性和任务成功性。
由于送往基地的维修项目难度较大,完成此项维修工作的时间较长,修理系统的组建和出动的时间相对显得很短,故可忽略不计。基地级维修机构和中继级维修机构所服务的对象都是舰艇及相关的武器装备,因而具有相同的维修保障能力的效能评估指标。
在MAS仿真架构中,基地级维修Agent的人力、设备、设施、技术资料、备品备件等资源的利用率,受到中继级维修分队Agent的影响,但在仿真统计时只看基地级维修资源是否是被利用上,而不统计这种影响力。在考察基地级维修保障资源利用率指标时,各个资源的投入及时率和导致的延迟相对于该项目维修时长来说是微小的,可忽略不计。除此之外,基地级维修资源的其他指标的求解与中继级相同。
5 结束语
为了以最小的费用在最短的时间内达到最佳的维修效果,在针对维修保障修理机构的人力、设备、设施、技术资料、备品备件等资源进行基于MAS仿真时,各维修机构Agent会通过共享和重组这些资源。在考虑仿真中会发生共享和重组的情况下,逐一建立各维修资源利用率指标并给出了求解计算模型,明确了对仿真中间数据和仿真软件的开发的要求。
参考文献:
[1]王蕴.基于模糊熵的装备保障性评估模型[J].火力与指挥控制,2009,34(4):22-24.WANG YUN.The evaluation model of the supportability based on fuzzy entropy[J].Fire Control&Command Control,2009,34(4):22-24.(in Chinese)
[2]金荣.基于熵权多目标决策的保障性评价方法研究[J].空军工程大学学报:自然科学版,2007,8(3):56-59.JIN RONG.An evaluation method of supportability based on entropy weight multi-objective decision making[J].Journal of Air Force Engineering University:Natural Science Edition,2007,8(3):56-59.(in Chinese)
[3]关楠.基于灰色理论的装备保障性评价数学分析方法研究[J].青岛大学学报:自然科学版,2006,19(3):7-11.GUAN NAN.Guarantee-nature-engineering evaluation base on grey system theory[J].Journal of Qingdao University:Natural Science Edition,2006,19(3):7-11.(in Chinese)
[4]李红江,张晓锋,焦绍光,等.舰船电力系统可靠性研究[J].武汉理工大学学报:交通科学与工程版,2006,30(6):931-934.LI HONGJIANG,ZHANG XIAOFENG,JIAO SHAOGUANG,et al.Primer research of the warship power system reliability[J].Journal of Wuhan University of Technology:Transportation Science&Engineering,2006,30(6):931-934.(in Chinese)
[5]霍综斌,刘维亭,梁世清.舰船环形区域配电网络结构可靠性分析[J].舰船科学技术,2008,30(5):28-31.HUO ZONGBIN,LIU WEITING,LIANG SHIQING.Reliability analysis of structure of warships closed loop zonal distribution system[J].Ship Science and Technology,2008,30(5):28-31.(in Chinese)
[6]杨祖萍,李永春.舰船通信控制管理系统的可靠性设计[J].环境适应性与可靠性,2009(3):28-31.YANG ZUPING,LI YONGCHUN.Reliability design of communication controlling management system for warship[J].Environmental Adaptability and Reliability,2009(3):28-31.(in Chinese)
[7]周卫东,郝燕玲,陈广,等.舰船组合导航应用软件可靠性指标分配[J].弹箭与制导学报,2006,26(1):786-788.ZHOU WEIDONG,HAO YANLING,CHEN GUANG,et al.Software reliability allocation of warship integrated navigation[J].Journal of Projectiles,Rockets,Missiles and Guidance,2006,26(1):786-788.(in chinses)
[8]金星,张明亮,王军,等.大型复杂系统可靠性评定的近似计算方法[J].装备指挥技术学院学报,2004,15(5):53-56.JIN XIN,ZHANG MINGLIANG,WANG JUN,et al.An approximate method of reliability evaluation for largescale complicated system[J].Journal of the Academy of Equipment Command&Technology,2004,15(5):53-56.(in Chinese)
[9]杨秉喜,张义芳,熊勇.备件需求量计算模型及其在地面雷达中的应用[J].电子产品可靠性与环境试验,2000(6):13-17.YANG BINGXI,ZHANG YIFANG,XIONG YONG.Calculation models of spares and their application in the ground rader[J].Electronic Product Reliability and Environmental Testing,2000(6):13-17.(in Chinese)
[10]王苏平,廖向红.维修用零备件使用量预测技术[J].航空工程与维修,2001(11):28-29.WANG SUPING,LIAO XIANGHONG,Forecast technology for maintenance parts usage[J].Aviation Maintenance&Engineering,2001(11):28-29.(in Chinese)
[11]周江华,肖刚,孙国基.N:K系统可靠度及备件量的仿真计算方法[J].系统仿真学报,2001,13(2):161-164.ZHOU JIANGHUA,XIAO GANG,SUN GUOJI.Simulation-based method for computation reliability and optimum quantity of N:K(m)cross-strapping standby system[J].Journal of System Simulation,2001,13(2):161-164.(in Chinese)
[12]张建军,李树芳,张涛,等.备件保障度评估与备件需求量模型研究[J].电子产品可靠性与环境试验,2004(6):18-22.ZHANG JIANJUN,LI SHUFANG,ZHANG TAO,et al.Study on spare availability and optimization model[J].Electronic Product Reliability and Environmental Testing,2004(6):18-22.(in Chinese)
[13]WOOLDRIDGE M,JENNINGS N R,KINNY D.The gaia methodology for agent-oriented analysis and design[J].Journal ofAutonomousAgents and Multi-Agent Systems,2000,3(3):285-312.
[14]CAVALIERI S,GARETTI M,MACCHI M,et al.An experimental benchmarking of two multi-agent architectures for production scheduling and control[J].Computers in Industry,2000,43:139-152.
[15]RABELO R J,CANARINHA-MATOS L M.Negotiation in multi-agent based dynamic robotics and computer integrated manufacturing[J].Computers in Industry,1994,11(4):303-309.
[16]SYCARA K,PANNU A,WILLAMSON M,et al.Distributed intelligent agents[J].IEEE Expert,1996,11(6):36-46.
[17]DAVIS R,SMITH R G.Negotiation as a metaphor for distributed problem solving[J].Artificial Intelligence,1983,20:63-109.
[18]冯申,杨自春.以可用度为中心的舰艇单部件系统备件配置的Monte-Carlo仿真方法[J].中国造船,2005,46(3):117-120.FENG SHEN,YANG ZICHUN.Monte-Carlo simulating method for the spare parts allocation model centered availability of the single part system on naval ship[J].Shipbuilding of China,2005,46(3):117-120.(in Chinese)

