含风电的交直流互联电网AGC两级分层模型预测控制
廖小兵, 刘开培, 汪宁渤, 马彦宏, 陈 钊, 丁 坤, 周 强, 秦 亮
(1. 武汉大学电气工程学院, 湖北省武汉市 430072; 2. 国网甘肃省电力公司风电技术中心, 甘肃省兰州市 730050)
0 引言
自动发电控制(AGC)是能量管理系统中的一项重要功能,它按照一定的调节速率实时调整发电机组出力,以满足电力系统频率和联络线功率控制的要求[1-2]。随着规模化风电接入交直流互联电网,这对AGC系统的控制性能提出了更高的要求,以适应大规模风电出力的随机性和间歇性[3]。
为实现AGC系统的控制目标,国内外研究人员已提出了许多控制方法和策略。目前,应用最为广泛的控制算法主要是基于智能优化技术的比例—积分—微分(PID)控制方法[4-7]、基于微分博弈理论的控制方法[8-10]、模型预测控制(MPC)[11-13]等三类。基于智能优化技术的PID控制方法是在经典PID结构的基础上对控制器参数采用智能优化方法进行整定,以达到最优的控制性能,比如采用遗传算法[4]、粒子群优化算法[5]、混合智能算法[6]等对控制器参数进行优化整定。基于微分博弈理论的控制方法将博弈理论和最优控制理论相结合,通过多方博弈达到纳什均衡的控制策略。这两类方法都要求建模精度高,且不易处理复杂、多变量的约束条件。MPC是近年来被广泛应用于AGC系统的一类反馈控制策略,具有系统模型要求低、控制性能好、在线优化便捷、能处理多变量约束等优点[14],成功地应用于AGC系统控制器设计。
MPC方法根据制器结构分为:集中式模型预测控制(CMPC)[15]、分散式模型预测控制(DMPC)[16-17]、分层式模型预测控制(HMPC)[18-19]三大类。CMPC是将整个系统的所有输出或状态信息反馈到一个中央控制器上,控制器计算得到整个系统的控制输入,这种控制方式的优点是系统结构简单,但在计算量、可靠性等方面能力十分有限。为此,文献[20-22]通过将整个AGC系统划分为多个互相耦合的子系统,每个子系统由一个独立的控制器控制,提出了鲁棒性好、收敛性快的DMPC方法。DMPC是由分散在各个区域内MPC控制器根据系统状态信息和区域控制偏差(ACE)信号计算得到相应的控制量,并分配至区域内AGC机组,实现互联电网AGC系统的分散控制[17]。DMPC方法通过多个控制器可以提高系统的可扩展性以及系统的容错能力,解决了子系统地理分布上的分散性。HMPC是将集中式控制方式和分散式控制方式有机相结合,通过上下层之间的递进关系切换控制方式,因而,HMPC兼有集中式控制和分散式控制的优点,是一类控制性能优异、高可靠性的先进控制方式[19]。
本文将HMPC应用于含规模化风电的交直流互联电网AGC系统控制器设计,提出了一类两级分层的MPC策略,兼具了集中式控制的全局最优性和分散式控制方式的可扩展性。在建立含多电源的两区域交直流互联电网AGC模型的基础上,通过在MATLAB/Simulink平台上的仿真结果验证了本文所提策略的优异控制性能和高可靠性。
1 含多电源的交直流互联电网AGC模型
本文以含多电源的交直流互联电网作为研究对象,交直流互联电网区域i的AGC模型的传递函数框图[23]如图1所示。其中,区域i由再热式火电机组、水轮机组、燃气轮机组和风电机组构成,区域之间通过交直流并联联络线实现互联,三类AGC机组模型的传递函数框图参数说明在文献[23]有详细说明,这里亦不再赘述。图中:Ai为ACE信号;ΔPci为AGC机组原动机功率调节量;Rgi,Rhi,Rti为三类AGC机组的调差系数;ΔXti和ΔPRti分别为汽轮机调速器位置偏差和再热发电机组输出热功率增量;ΔXRHi和ΔXhi分别为水轮机调速器位置偏差和水轮机阀门调节输出功率增量;ΔXgi,ΔXVPi,ΔPRgi分别为阀门定位器位置偏差、汽轮机调速器位置偏差和汽轮机阀门调节输出功率增量;Kti,Khi,Kgi为三类AGC机组的功率分配系数;ΔPwi为风电场输出功率实际值与预测值偏差;ΔPLi为负荷功率变化量;ΔPGti,ΔPGhi,ΔPGgi为三类AGC机组的实际出力变化量;Tij为联络线同步系数;Kpi为负荷频率调节效应系数;Tpi为惯性时间常数;Δfi为频率偏差。根据图1中的传递函数模型分别推导形成再热式火电机、水轮机、燃气轮机的状态空间模型如下。
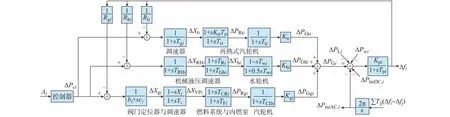
图1 交直流互联电网区域i的AGC模型Fig.1 AGC model for control area i of AC/DC interconnected power grid
再热式火电机机组状态空间模型为:
(1)


(2)
(3)
水轮机机组状态空间模型为:
(4)

(5)

(6)
燃气轮机组状态空间模型为:
(7)
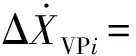
(8)

(9)
(10)
区域i与区域j之间的交流联络线功率偏差变化率为:
(11)
则区域i与其他区域间通过交流线路交换的有功功率偏差变化率可表示为:
(12)
本文考虑区域i与区域j之间存在直流线路交换有功功率,可表示为:
(13)
即
(14)
则区域i与其他区域间通过直流线路交换的有功功率偏差变化率为:
(15)
因此,区域i的频率偏差变化率为:
(16)
ΔPGi=ΔPGti+ΔPGhi+ΔPGgi
(17)
ΔPtie,i=ΔPtieAC,i+ΔPtieDC,i
(18)
各个区域的ACE信号Ai由本区域的频率偏差和净交换功率偏差综合构成,定义ACE信号为:
Ai=βiΔfi+ΔPtie,i
(19)
至此,可得到区域i的状态空间模型为:
(20)
式中:yi,xi,ui,di分别为输出变量、状态变量、控制变量、扰动变量;Ai,Bi,Ei,Ci为相应的系统矩阵参数,具体元素见附录A。
2 AGC的两级分层MPC策略
2.1 MPC方法
MPC算法由于采用了多步预测、滚动优化和反馈校正等控制策略,因而具有控制性能好、鲁棒性强、对模型精确性要求不高的优点[14],其基本原理可用图2描述。

图2 MPC的基本原理Fig.2 Basic principle of MPC
从图2中可以看出:MPC主要分为多步模型预测、滚动优化和反馈校正三个步骤。首先通过将式(20)离散化得到离散状态空间模型:
(21)

基于离散状态空间模型(式(21)),可推导出系统起始于yi(k)的未来一段时间内的模型输出yi(k+j|k)(j∈(1,p),其中p为预测时域)。在控制时域m(m≤p)内,通过构造二次型性能指标函数:
(22)
式中:qj和rj分别为输出加权因子和控制加权因子;Ri为参考轨迹值,在AGC系统中即为ACE信号,其控制目标值全为0。
通过求解二次性能指标函数(式(22))来确定未来的控制作用动作序列ui(k+j-1|k)(j∈(1,m)),再将控制动作序列中的第一个控制序列ui(k)作用于系统,并求解刷新后的优化问题,如此循环向前推进。因此,MPC是一类滚动时域优化控制策略,通过在线求解相对简单的开环优化问题,采用滚动优化机制得到最优控制的一个闭环解。
2.2 基于广域测量系统的两级分层控制策略
广域测量系统(WAMS)可为AGC系统快速地提供准确、可靠的数据[24]。在基于WAMS数据平台的基础上,本文提出一类两级分层的MPC策略,具体的控制策略框图如图3所示。下层采用DMPC,将多个MPC控制器分散在多个区域电网内,由WAMS向分散的MPC控制器传递各个区域电网的ACE信号,并将所有的ACE信号传递至上层控制器,这个区域电网的MPC控制器处理的信息量不大,可保证局部控制的快速性和可靠性;在上层的集中式MPC控制器根据所有ACE信号综合确定是否需要作用:通过给分散在各个区域的MPC控制器输入参考信号Ri(i=1,2,…,n)在不需要作用时参考信号Ri处于开断状态。
综上所述,下层分散的MPC控制器的控制变量函数为:
f(Ai-Ri)=ui
(23)
这里,Ri在不需要动作时置0。上层的集中式MPC控制是采用动态协调控制方式,即综合考虑所有ACE信号确定是否需要动作,这里将所有ACE信号的均方根作为参考值,只有大于参考值时才允许动作,因此,这种动态机制一方面有利于减少上层集中式MPC控制器的动作次数,减少计算量;另一方面,可以消除分散的MPC控制器间的调整动作冲突,实现全局协调和监控。基于WAMS的两级分层控制框架结合实际区域电网AGC系统局部自治、分散控制的特点,进一步设计上层协调控制器,实现各个区域电网协调控制,能充分利用各个区域电网的AGC系统调节资源来消纳大规模风电。因此,基于WAMS的两级分层控制框架具有很好的实际工程意义。

图3 基于MPC的交直流互联电网两级分层控制框图Fig.3 Two-level hierarchical control diagram of AC/DC interconnected power grid based on MPC
3 仿真分析
3.1 仿真系统设置
为验证本文所提出的基于两级分层MPC策略的有效性,采用MALTAB/Simulink平台对如图4所示的含多电源的两区域交直流互联电网AGC系统进行仿真研究。区域电网1和2中的AGC模型参数见附录B。

图4 含多电源的两区域交直流互联电网Fig.4 Two-area AC/DC interconnected power grid with multiple power sources
本文所有MPC控制器相关参数如下:离散点采样周期为0.1 s,预测时域p=20,控制时域m=10,输出加权因子为1,控制加权因子为0.1。
本文将分别采用CMPC方式[15]、DMPC[17]方式和本文所提出的两级HMPC方式进行对比仿真分析。通过设置风功率随机波动场景、负荷阶跃场景和WAMS通信故障场景的仿真测试来验证本文所提出的控制策略的有效性。
3.2 风功率随机波动场景分析
假设在仿真时段内不同风电规模的输出的功率实际值与预测值之间偏差的标幺值如图5所示。当区域电网1接入风电场装机容量为400 MW时,两区域AGC系统动态时域响应曲线见附录C图C1。可以看出,相比于其他两种控制方法,本文所提出的控制方法具有更好的动态时域响应。采用CMPC,DMPC,HMPC三种控制方法时区域电网1的最大频率偏差分别为0.177,0.059,0.038 Hz;而区域电网2的最大频率偏差分别为0.173,0.058,0.027 Hz。这里采用DMPC方式的控制效果要优于CMPC方式,主要是由于DMPC方式将与区域i互联的频率偏差总和信号传递给区域i作为一个随机扰动信号,实现了各个区域电网分散协调控制,因此,DMPC方式实质上是分散协调控制方式,具有较CMPC方式更好的控制效果。因此,本文所提出的HMPC策略能更加有效地抑制联络线功率的振荡,维持大规模风电场接入交直流电网的频率稳定。

图5 不同风电规模的输出功率实际值与预测值偏差Fig.5 Deviations between wind power actual values and predicted values under different scale wind power capacities
本文进一步测试了当风电装机容量分别为400,600,800 MW时,两区域电网的频率偏差响应曲线,具体见附录C图C2。不难看出:随着风电场规模的扩大,风电场的输出有功功率偏差的波动幅度越大,造成两个区域电网的频率响应曲线波动幅度也增大,尤其是区域电网1的频率在风电装机容量为800 MW时已经超过了允许值。
3.3 负荷阶跃场景分析
在20 s时刻对区域电网1施加0.1(标幺值)的负荷阶跃扰动,在50 s时刻对区域电网2施加0.3的负荷阶跃扰动,这里假设区域电网1和2的AGC调节容量为0.25。在这类负荷阶跃扰动场景下,两区域AGC系统动态时域响应曲线见附录C图C3。从这4幅图中不难发现:相比CMPC和DMPC这两类控制方法,本文所提出的HMPC策略不仅能够使得系统频率偏差和交直流联络线功率偏差更快速地恢复至稳态,而且可以有效地降低系统频率偏差幅值和交直流联络线功率偏差幅值。由于区域电网2出现AGC机组调节容量有限,通过修改交流联络线协议,使得区域电网1三个AGC机组增发的0.05通过交流联络线输送至区域电网2,因此,交流联络线的恢复至稳态时偏差为0.05。
附录C图C4给出了区域电网1中三类AGC机组的出力变化曲线。本文在每次滚动优化过程中考虑机组的爬坡速率、容量约束,从这3幅图可以看出:各AGC机组的发电量均未超过它们在AGC系统中所占的比例。采用HMPC方式的三类AGC机组实现了较高的发电爬坡速率,比采用DMPC和CMPC更快达到预定发电量。
3.4 WAMS通信故障场景分析
在实际电力系统中,基于WAMS平台的通信可能由于故障造成AGC系统无法正常工作,进而造成系统的稳定运行。为此,本节将验证本文所提出的基于两级分层的MPC策略的高可靠性,能保证WAMS通信故障下系统的安全稳定。
假设WAMS通信故障造成中央集中式MPC控制器无法对区域电网实施控制作用,即当ΔPc1=0时,失去了对区域电网1的控制,即当ΔPc1=0,ΔPc2=0时,失去了对两区域电网的控制,假设在20 s时刻对区域电网1施加0.1的负荷阶跃扰动,在50 s时刻对区域电网2施加0.2的负荷阶跃扰动,在负荷阶跃时刻时发生通信故障。两区域AGC系统动态时域响应曲线见附录C图C3。
在这两种情况下两区域电网的频率偏差曲线见附录C图C5。从图中可以看出:在集中式MPC控制器部分或全部失效时,本文所提出的两级分层控制策略由于下层分散的MPC控制器的作用,依然可以维持系统的频率稳定。
同样,假设WAMS通信故障造成分散式MPC控制器无法对区域电网实施控制作用,即当ΔPc1=0时,失去了对区域电网1的控制,即当ΔPc1=0,ΔPc2=0时,失去了对两区域电网的控制,在这两种情况下两区域电网的频率偏差曲线见附录C图C6。从图中可以看出:在分散式MPC控制器部分或全部失效时,本文所提出的两级分层控制策略由于上层集中式的MPC控制器作用,依然有能力可以维持系统的频率稳定。
通过上述两个通信故障情景的仿真分析,本文所提出的两级分层控制策略实现了上层集中式控制和下层分散式控制,能够在不同的通信故障下切换控制方式,以维持系统的频率稳定,所以该控制策略具有很高可靠性。
4 结论
为应对大规模风电接入交直流互联电网所带来的AGC控制问题,本文提出了基于两级分层的MPC器设计方案。通过含多电源的两区域交直流互联电网AGC系统动态仿真结果可以得出以下结论。
1)在风电功率波动和负荷阶跃场景下,本文所提出的基于两级分层MPC策略不仅能够维持频率和交直流联络线交换功率在较小的范围内波动,而且控制效果明显优于CMPC和DMPC这两类控制策略。
2)在WAMS通信故障场景下,本文提出的控制策略通过上下层控制器的切换实现分散控制和集中控制,具有很高的可靠性。
在建立风电场的详细AGC模型基础上,并将其纳入跨区域AGC机组经济性调频控制,既能提高风电场的可调度性,又能改善电网的AGC经济性,因此,基于两级分层MPC的AGC经济性跨区协调控制是今后需要进一步开展的研究工作。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
参考文献
[1] 《电力系统调频与自动发电控制》编委会.电力系统调频与自动发电控制[M].北京:中国电力出版社,2006:5-8.
[2] 颜伟,赵瑞锋,赵霞,等.自动发电控制中控制策略的研究发展综述[J].电力系统保护与控制,2013,41(8):149-155.
YAN Wei, ZHAO Ruifeng, ZHAO Xia, et al. Review on control strategies in automatic generation control[J]. Power System Protection and Control, 2013, 41(8): 149-155.
[3] 倪琳娜,罗吉,王少荣.含风电电力系统的频率控制[J].电工技术学报,2011,26(增刊1):235-241.
NI Linna, LUO Ji, WANG Shaorong. Frequency control of power system with wind power integration and dynamic stability[J]. Transactions of China Electrotechnical Society, 2011, 26(Supplement 1): 235-241.
[4] PANDA S, YEGIREDDY N K. Automatic generation control of multi-area power system using multi-objective non-dominated sorting genetic algorithm-Ⅱ[J]. International Journal of Electrical Power & Energy Systems, 2013, 53: 54-63.
[5] SAHU R K, PANDA S, SEKHAR G T C. A novel hybrid PSO-PS optimized fuzzy PI controller for AGC in multi area interconnected power systems[J]. International Journal of Electrical Power & Energy Systems, 2015, 64: 880-893.
[6] SAHU R K, PANDA S, PADHAN S. A hybrid firefly algorithm and pattern search technique for automatic generation control of multi area power systems[J]. International Journal of Electrical Power & Energy Systems, 2015, 64: 9-23.
[7] 谢平平,李银红,刘晓娟,等.基于社会学习自适应细菌觅食算法的互联电网AGC最优PI/PID控制器设计[J].中国电机工程学报,2016,36(20):5440-5448.
XIE Pingping, LI Yinhong, LIU Xiaojuan, et al. Optimal PI/PID controller design of AGC based on social learning adaptive bacteria foraging algorithm for interconnected power grids[J]. Proceedings of the CSEE, 2016, 36(20): 5440-5448.
[8] 叶荣,陈皓勇,卢润戈.基于微分博弈理论的两区域自动发电控制协调方法[J].电力系统自动化,2013,37(18):48-54.
YE Rong, CHEN Haoyong, LU Runge. A differential games theory based method for coordinating two-area automatic generation control[J]. Automation of Electric Power Systems, 2013, 37(18): 48-54.
[9] 卢润戈,陈皓勇,叶荣,等.电力系统一二次调频的反馈微分博弈协同控制[J].控制理论与应用,2014,31(9):1182-1189.
LU Runge, CHEN Haoyong, YE Rong, et al. Feedback differential game cooperative control for primary and secondary frequency control of power system[J]. Control Theory & Applications, 2014, 31(9): 1182-1189.
[10] 伍亮,杨金明.基于微分博弈理论的含多电源区域电力系统负荷频率控制[J].中国电机工程学报,2014,34(16):2676-2683.
WU Liang, YANG Jinming. Load frequency control of area power system with multi-source power generation based on differential games theory[J]. Proceedings of the CSEE, 2014, 34(16): 2676-2683.
[11] 刘向杰,孔小兵.电力工业复杂系统模型预测控制:现状与发展[J].中国电机工程学报,2013,33(5):79-85.
LIU Xiangjie, KONG Xiaobing. Present situation and prospect of model predictive control application in complex power industrial process[J]. Proceedings of the CSEE, 2013, 33(5): 79-85.
[12] 张颖,季宇,唐云峰,等.基于MPC含分布式光伏配电网有功功率-无功功率协调控制[J].电力系统自动化,2017,41(21):140-146.DOI:10.7500/AEPS20161226001.
ZHANG Ying, JI Yu, TANG Yunfeng, et al. Coordinate control of active and reactive power for distribution network with distributed photovoltaic based on model predictive control[J]. Automation of Electric Power Systems, 2017, 41(21): 140-146. DOI: 10.7500/AEPS20161226001.
[13] ERSDAL A M, IMSLAND L, UHLEN K. Model predictive load-frequency control[J]. IEEE Transactions on Power Systems, 2015, 31(1): 777-785.
[14] 陈虹.模型预测控制[M].北京:科学出版社,2013:1-12.
[15] 陈来军,王任,郑天文,等.改善独立微网频率动态特性的虚拟同步发电机模型预测控制[J].电力系统自动化,2018,42(3):40-47.DOI:10.7500/AEPS20170312003.
CHEN Laijun, WANG Ren, ZHENG Tianwen, et al. Model predictive control of virtual synchronous generator to improve frequency dynamic characteristic of isolated microgrid[J]. Automation of Electric Power Systems, 2018, 42(3): 40-47. DOI: 10.7500/AEPS20170312003.
[16] MOHAMED T H, BEVRANI H, HASSAN A A, et al. Decentralized model predictive based load frequency control in an interconnected power system[J]. Energy Conversion & Management, 2011, 52(2): 1208-1214.
[17] 杨德友,蔡国伟.含规模化风电场/群的互联电网负荷频率广域分散预测控制[J].中国电机工程学报,2015,35(3):583-591.
YANG Deyou, CAI Guowei. Decentralized model predictive control based load frequency control for high wind power penetrated power systems[J]. Proceedings of the CSEE, 2015, 35(3): 583-591.
[18] 张伯明,陈建华,吴文传.大规模风电接入电网的有功分层模型预测控制方法[J].电力系统自动化,2014,38(9):6-14.DOI:10.7500/AEPS20130712012.
ZHANG Boming, CHENG Jianhua, WU Wenchuan. A hierarchical model predictive control method of active power for accommodating large-scale wind power integration[J]. Automation of Electric Power Systems, 2014, 38(9): 6-14. DOI: 10.7500/AEPS20130712012.
[19] WANG D, GLAVIC M, WEHENKEL L. Comparison of centralized, distributed and hierarchical model predictive control schemes for electromechanical oscillations damping in large-scale power systems[J]. International Journal of Electrical Power & Energy Systems, 2014, 58: 32-41.
[20] LIU X, ZHANG Y, LEE K Y. Robust distributed MPC for load frequency control of uncertain power systems[J]. Control Engineering Practice, 2016, 56(1): 136-147.
[21] LIU X, ZHANG Y, LEE K Y. Coordinated distributed MPC for load frequency control of power system with wind farms[J]. IEEE Transactions on Industrial Electronics, 2017, 64(6): 5140-5150.
[22] LIU X, KONG X, LEE K. Distributed MPC for load frequency control with dynamic fuzzy valve position modeling for hydro-thermal power system[J]. IET Control Theory & Applications, 2016, 10(14): 1653-1664.
[23] IBRAHEEM, NIZAMUDDIN, BHATTI T S. AGC of two area power system interconnected by AC/DC links with diverse sources in each area[J]. International Journal of Electrical Power & Energy Systems, 2014, 55: 297-304.
[24] TERZIJA V, VALVERDE G, CAI D, et al. Wide-area monitoring, protection, and control of future electric power networks[J]. Proceedings of the IEEE, 2010, 99(1): 80-93.

