含虚拟惯量的电力系统频率响应特性定量分析方法
黄林彬, 辛焕海, 黄 伟, 杨 欢, 汪 震
(1. 浙江大学电气工程学院, 浙江省杭州市 310027; 2. 云南电网有限责任公司调度控制中心, 云南省昆明市 650011)
0 引言
随着新能源发电、储能应用、柔性直流输电等技术的发展,现代电力系统正逐渐演变为以电力电子设备高渗透率为特征的电力电子化电力系统[1-3]。由于电力电子设备与传统同步发电机具有完全不同的物理结构,如同步发电机具有大惯量的旋转转子而逆变器是由电力电子开关器件所构成,因此在电力电子设备逐渐替代同步发电机作为电源的过程中,必然也逐渐地改变电力系统的特征。
其中十分明显的一点是,传统电力系统中的频率由同步发电机的转子转速决定,同步发电机的转子旋转惯量十分巨大,决定了系统频率在扰动下(例如有功功率扰动)的波动很小,且该旋转惯量可以对系统提供有功功率支撑,因此传统电力系统具有非常好的频率响应特性[4]。但是随着电力电子设备渗透率的不断提高,同步机比例逐渐减小,电力系统逐渐失去了维持系统频率的“转子”。由此带来的后果将是电力系统在扰动下频率波动变大,频率稳定性变差,抵御大扰动(如交流短路、直流闭锁等)的能力大为降低[5]。特别地,当逆变器采用恒功率控制时,可视为一个功率源,此时它无法参与系统的频率调节或提供频率支撑[6],从而呈现“不友好”的并网特性。
为了应对这一问题,国内外学者提出了“虚拟同步机”的逆变器控制方式[7-9],旨在利用逆变器灵活可控的特点,通过控制使逆变器具有类似于同步发电机的外特性。值得一提的是,虚拟同步机的控制思想可以广泛地应用于新能源发电、储能技术以及柔性直流输电技术中,使电力系统中的电力电子设备广泛地参与到系统的频率调节中,而这其中主要以虚拟惯量的加入来改进系统的频率响应特性。
通过合理配置虚拟同步机的虚拟惯量以及电气阻尼系数可以改变其频率响应特性。目前,虚拟惯量与电气阻尼系数主要从小干扰稳定的角度进行选取,即通过配置虚拟惯量与电气阻尼优化单机系统的小干扰稳定性[9]。而在频率扰动的抑制方面,主要从时域仿真的角度说明虚拟惯量在减小系统频率波动方面的作用[10-12],但尚未有合理的指标用于定量评价虚拟惯量的加入对电力系统频率响应特性的影响。因此,当前难以定量地刻画虚拟惯量的加入对于提高电力系统频率扰动抑制能力的意义,亦无法定量地优化虚拟惯量在多虚拟同步机系统中的分配。
特别地,新能源并网设备中虚拟惯量的加入常常还需要考虑到如风机转子动态、锁相环动态或者直流电容动态等[13-16]。当前已有研究指出可以利用锁相环或直流电容的动态实现惯量模拟[5,17],可见,并网设备的多样性以及虚拟惯量模拟方式的多样性将使电力系统的频率响应特性分析更为复杂。
为此,本文利用系统相位扰动到频率输出的闭环传递函数的H2和H∞范数,定量研究逆变器的虚拟惯量的加入对于系统频率响应特性的影响。首先以同步发电机的特性作为对照研究虚拟同步机不同虚拟惯量与电气阻尼下的响应特性。在此基础上,进一步研究了多机系统中虚拟惯量的配置对于系统频率响应特性的影响。最后,利用仿真验证了理论分析结果的可信性。
1 同步发电机的频率响应特性
1.1 同步发电机的模型
考虑图1(a)所示的单机无穷大系统,发电机经线路为一电阻性负荷供电,再经线路连接到无穷大母线,该系统主要参数可参见附录A表A1。本文采用以电机参数表示的同步电机方程(需要指出的是,本文中列出的所有方程均是在标幺值下得出的),其转子绕组电压平衡方程与定子绕组电压平衡方程为[18]:
(1)
式中:Efq为励磁电压;id和iq为定子电流;vd和vq为机端电压;s为拉普拉斯算子;其余电机参数与变量的定义可参见文献[18]。
发电机的转子运动方程可写为:
(2)
式中:δ为同步机功角;ωSG为转子转速;f0为频率基准值50 Hz;HSG为惯量时间常数;PM为机械功率输入;PESG为电磁功率输出;DSG为机械阻尼系数。
在同步旋转坐标下的线路方程可写为[17]:
(3)
式中:LLine1,XLine1,RLine1和LLine2,XLine2,RLine2分别为线路1,2的电感、电抗和电阻;vd和vq、ud′和uq′、ud和uq分别为同步发电机机端电压、负载电压、无穷大母线电压的dq轴分量;id和iq、igd和igq分别为流过线路1、2的电流的dq轴分量;RLoad为负载电阻。
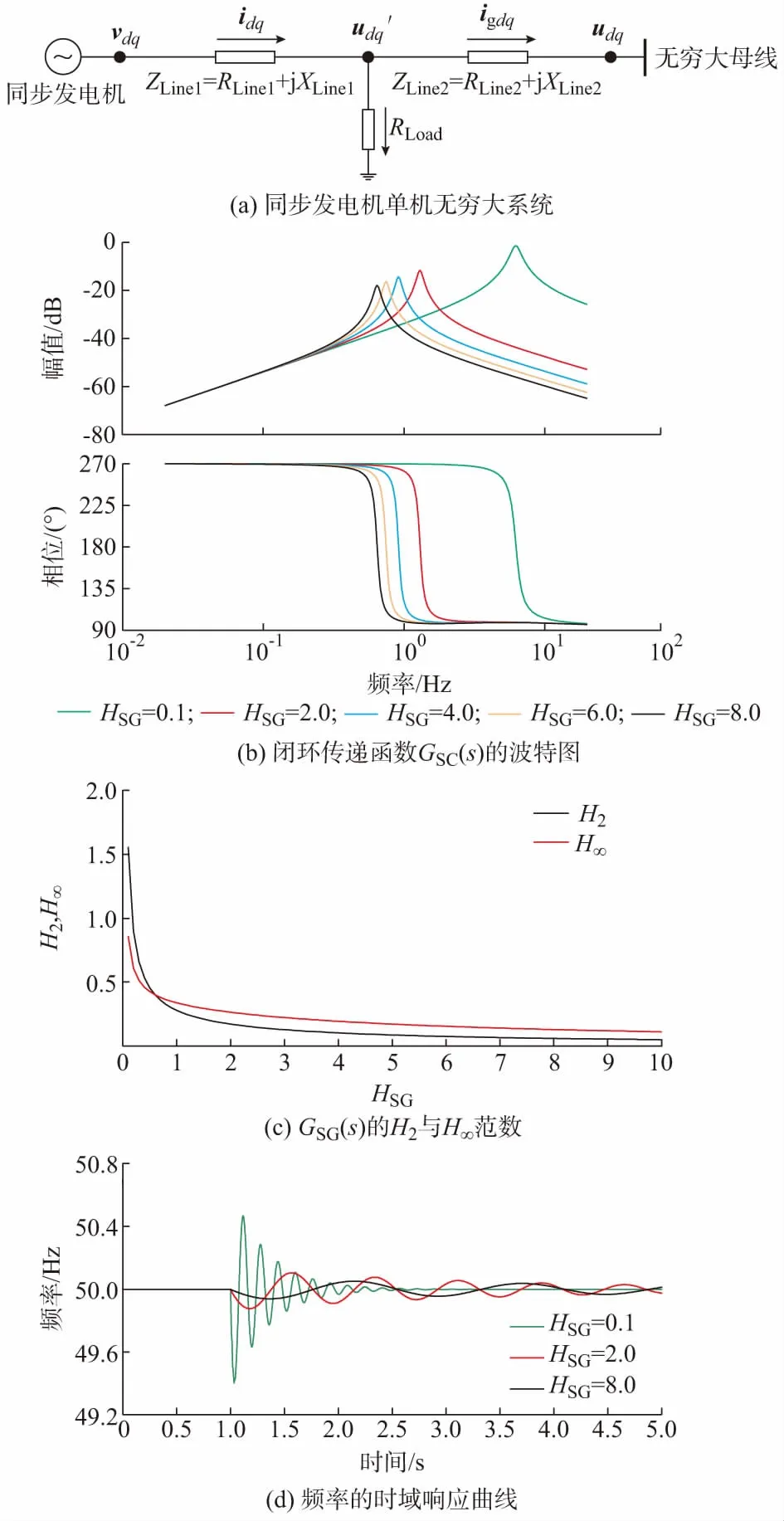
图1 同步发电机的频率响应特性Fig.1 Frequency response characteristics of synchronous generators
由于转子内电势位于d轴,因此在同步旋转坐标下无穷大母线的电压矢量可表示为:
(4)
式中:U=1.0(标幺值)为无穷大母线的电压矢量幅值。
需要指出的是,为简化分析,忽略调速器与励磁调节器的动态,即认为ΔEfq=0和ΔPM=0(Δ表示在平衡点上的扰动量),并且,由于本文针对研究系统的频率扰动抑制能力,本文选择系统输出为:
ΔySG=ΔωSG
(5)
扰动输入Δu加在同步机功角(相位)上,即
(6)
选择同步机相位扰动作为系统的输入是考虑到相对相位的变化等效于有功功率的变化[19],即等价于外电网电压的相位变化,而电力系统中有功功率的波动与频率波动呈现强相关。值得一提的是,选择相位扰动作为输入可以使本文所提出的指标方便地扩展到含锁相环并网设备的系统,这一点将在后续研究工作中进行进一步讨论。
将上述式(1)至式(6)在平衡点处线性化并消去代数变量即可得到同步发电机单机系统的状态空间模型,如式(7)所示。
(7)
值得指出的是,这里选择将同步发电机并入无穷大电网是出于研究单机系统频率特性的目的,因同步发电机并入无穷大电网将呈现摇摆特性。无穷大电网可以看作一个频率固定为50 Hz的理想电压源,根据文献[20]可知,系统中任意点的频率为该理想电压源频率与同步发电机频率的加权。特别地,当图1(a)中负荷消耗的功率来自于同步发电机时,流入无穷大母线的电流近似于零,此时负荷母线的频率近似地由同步发电机决定。
1.2 同步发电机的频率响应特性分析
由式(7)可进一步得出由相位扰动输入到频率输出的闭环传递函数为:
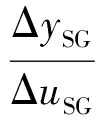
(8)
式中:I为单位矩阵。
传递函数GSG(s)代表了系统在全频带上的频率响应特性。图1(b)给出了惯量时间常数HSG取不同值时GSG(s)的波特图。可以看出,不同的HSG对应不同的谐振频率与峰值,HSG=0.1(标幺值)时系统的谐振频率约为6.1 Hz,HSG=2.0时系统的谐振频率约为1.2 Hz,HSG=8.0时系统的谐振频率约为0.61 Hz,其谐振峰值随着HSG的增大逐渐减小。
传递函数GSG(s)的谐振峰值对应其H∞范数,其物理意义为闭环系统对谐振频率的扰动的抑制能力。相比而言,H2范数则表示系统对于全频带的输入扰动的抑制能力,其物理意义为系统在白噪声激励下的输出特性。因此,本文通过闭环传递函数GSG(s)的H2与H∞范数两个指标来定量刻画系统的频率响应特性,分别表示系统频率在全频带上的扰动抑制能力以及在谐振频率上的扰动抑制能力。H2与H∞范数越小,系统频率的扰动抑制能力越强。
式(9)给出了传递函数G(s)的H2与H∞范数的计算公式[21],其中G(s)可以是传递函数矩阵,tr(A)表示矩阵A的迹,AH表示矩阵A的共轭转置,λmax(A)表示矩阵A的最大特征值。
(9)
图1(c)给出了GSG(s)的H2与H∞范数关于惯量时间常数HSG的变化规律。可以看出,随着HSG的增大,H2与H∞范数均单调递减,由此可以得出结论:同步发电机的惯量越大,其频率扰动抑制能力越强,该结论符合直观认识。
为了验证上述结论,图1(d)给出了图1(a)系统中同步发电机输出频率(转子电气转速)的响应曲线,在t=1 s时投入一个有功负荷(等效于相位扰动),造成同步机的频率输出波动。可以看出,在相同的扰动下,随着HSG从0.1增大到8.0,频率波动明显减小,从而验证了H2与H∞范数对于刻画系统频率扰动抑制能力的有效性。
本节分析了同步发电机的频率响应特性,旨在为后文中虚拟同步机的频率响应特性研究提供基准与参考,从而定量地对比同步发电机与虚拟同步机的频率响应特性。
2 虚拟同步机的频率响应特性
2.1 虚拟同步机的模型
当前不同虚拟同步机控制方式的差别主要在于电压、电流环的设计以及无功功率的控制,其共同点是相位控制由控制器中的转子运动方程所决定,这也是虚拟同步机的核心所在。因此,不失一般性,本文假定虚拟同步机采用电压外环电流内环的双环控制结构和无功功率—电压下垂控制[9,22]。并且,为了更好地提升系统动态特性,在虚拟同步机的控制中加入了虚拟阻抗[23-24],基本控制框图如图2所示。其中,虚拟同步机控制下的三相逆变器经过LCL滤波器给负荷供电,再经过线路连接到无穷大母线,系统的主要参数可参见附录A表A2。
由于含电压外环电流内环与虚拟阻抗的逆变器控制在很多文献中已经予以详细的描述与分析,如文献[17]等,因此本文不再赘述。本文主要关注虚拟同步机的转子运动方程,其控制实现如图2所示,控制方程可表示为:
(10)
式中:θ为同步旋转坐标相对于静止坐标的角度;ωVSG为虚拟同步机旋转坐标的角频率,可视为虚拟同步机的输出频率;HVSG为虚拟惯量时间常数;P0为有功功率设定值;PEVSG为虚拟同步机的输出电磁功率;D为等效的电气阻尼系数;ω0=1.0(标幺值)为角频率设定值(基准值为2πf0)。
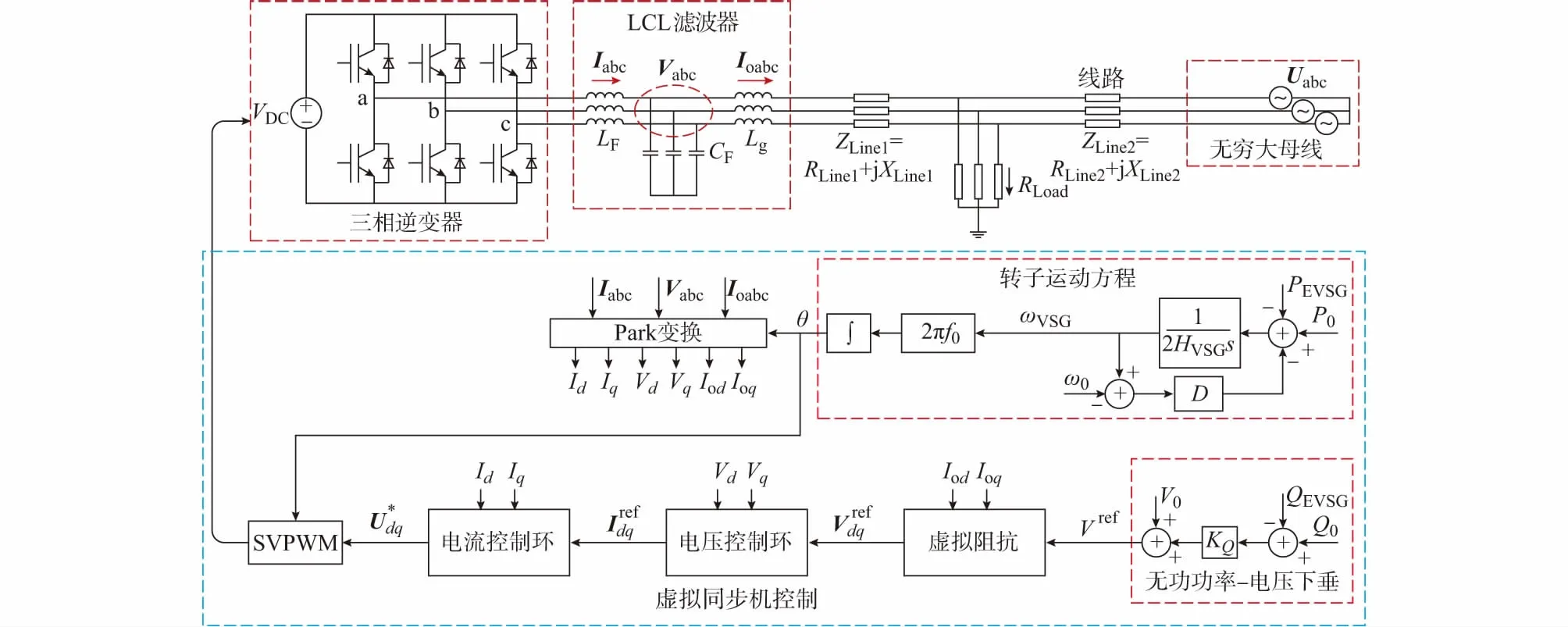
图2 虚拟同步机单机无穷大系统Fig.2 Single-machine infinite bus system of virtual synchronous generator
类似地,由于本文研究系统的频率扰动抑制能力,因此选择系统输出为:
ΔyVSG=ΔωVSG
(11)
扰动输入Δu加在相位上,即
(12)
可以看出,式(12)与式(6)具有类似的形式,即从转子运动方程的开环特性上看,虚拟同步机与同步发电机具有相似的频率响应特性。但即使如此,仍不能说明两者的闭环频率响应特性一致,因为虚拟同步机中还需要考虑电压电流控制、谐波的抑制以及LCL滤波器的响应特性,而同步发电机中没有这些问题。
含电压电流控制环及虚拟阻抗的逆变器小信号模型已经得到广泛的研究,在诸多文献中均有详细的推导(如文献[17,25]等),因此限于篇幅本文不再赘述。当选定式(11)和式(12)所示的系统输入输出后,图2的虚拟同步机系统的状态空间模型可表示为:
(13)
2.2 虚拟同步机的频率响应特性
由式(13)可进一步得到虚拟同步机的相位扰动到频率输出的闭环传递函数为:
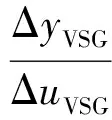
(14)
与同步发电机不同的是,虚拟同步机转子运动方程中的虚拟惯量HVSG与电气阻尼D可以自由设置而不受物理条件的约束,从而保证虚拟同步机有期望的动态性能。由于HVSG与D均对虚拟同步机的频率响应特性有影响,下文中将研究这两个参数的配置。
图3(a)中给出了闭环传递函数GVSG(s)在不同虚拟惯量HVSG时的波特图,可以看出,不同的虚拟惯量对应不同的谐振频率,HVSG=0.1(标幺值)时系统的谐振频率约为6 Hz,HVSG=2.0时系统的谐振频率约为1.2 Hz,HVSG=8.0时系统的谐振频率约为0.6 Hz,且其谐振峰值随着HVSG的增大基本维持不变,也就是说,GVSG(s)的H∞范数随虚拟惯量变化很小。对比图1(b)与图3(a)可知,当同步发电机的惯量时间常数HSG与虚拟同步机的虚拟惯量时间常数HVSG相等时,同步发电机与虚拟同步机具有十分接近的谐振频率,但谐振峰值不一致。
图3(b)给出了闭环传递函数GVSG(s)在不同电气阻尼D下的波特图,可以看出,不同的阻尼系数下谐振峰值发生改变,而谐振频率维持不变,即GVSG(s)的H∞范数与阻尼系数呈强相关。因此,合理配置电气阻尼可以使虚拟同步机的频率响应逼近同步机的响应。例如在HSG=HVSG=4.0,D=4时,GVSG(s)的谐振频率与谐振峰值与GSG(s)均十分接近。图3(c)给出了此时同步发电机与虚拟同步机的频率响应曲线,施加的扰动均为为t=1 s时投入一个有功负荷(等效于相位扰动),可见,同步发电机与虚拟同步机的响应几乎一致。

图3 虚拟同步机的频率响应特性Fig.3 Frequency response characteristics of virtual synchronous machines
若进一步将D从4增大到40,则GVSG(s)的谐振峰值下降,系统可以获得更好的响应。图3(c)给出了此时虚拟同步机的响应曲线,可以看出,在相同的扰动下,阻尼系数的增大更好地抑制了频率的波动,而且系统的阻尼特性变得更好,虚拟同步机此时具有优于同步发电机的频率响应特性。
2.3 虚拟同步机频率响应特性的H2与H∞范数分析
图4(a)给出了GVSG(s)的H2与H∞范数随HVSG和D变化的三维曲面图。可以看出:①H∞范数主要受D的影响并随D的增大而减小,而HVSG的增大使H∞范数略有增大(特别是在D较小的时候);②增大HVSG与D均能使H2范数减小,且HVSG的作用更大。由于H2范数表征了系统在全频带上的扰动抑制,因此与超调量较相关;而H∞范数则是在特征频率上的扰动抑制能力,因此与系统的阻尼特性更相关。也就是说,虚拟惯量系数HVSG主要影响系统频率响应的超调,增大HVSG可以减少超调量;等效电气阻尼系数D主要影响系统频率响应的阻尼,增大D可以增大频率响应的阻尼(衰减速率)。
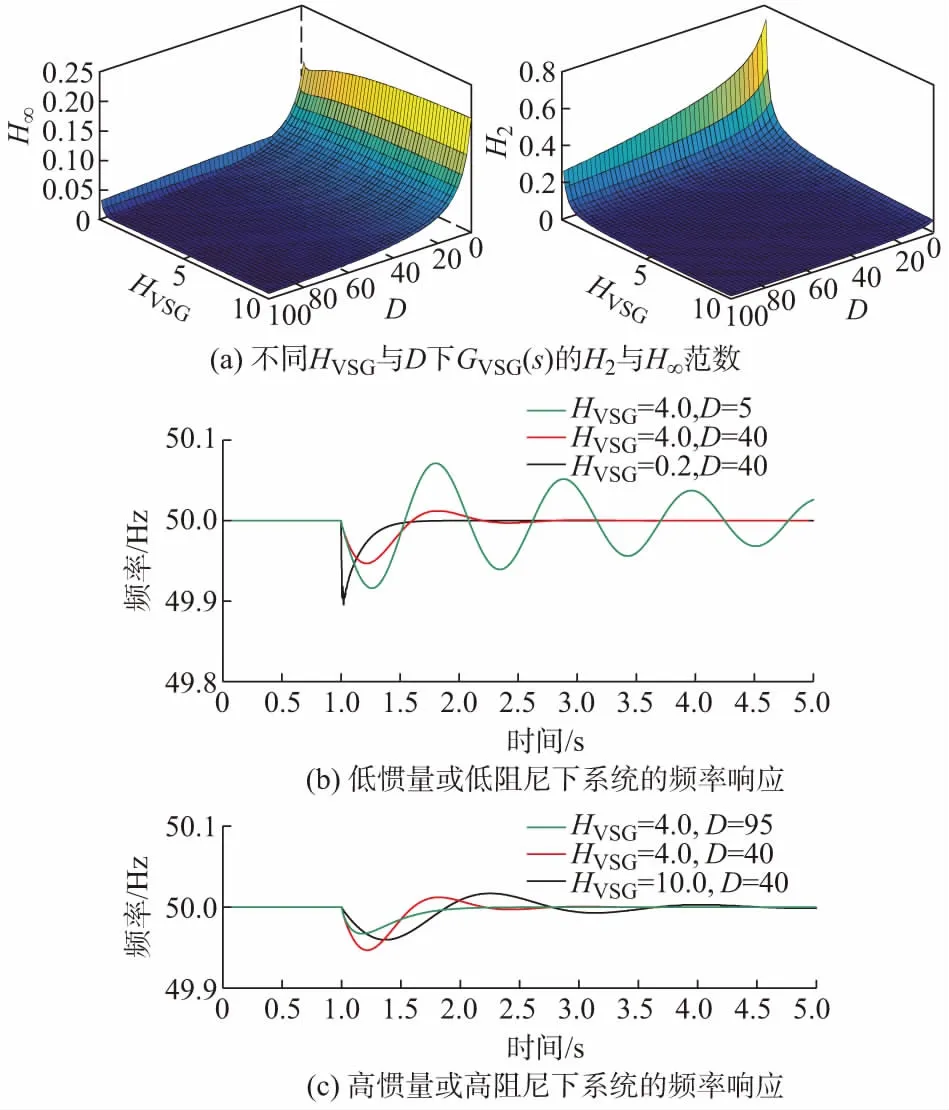
图4 不同虚拟惯量与阻尼下虚拟同步机的频率响应特性Fig.4 Frequency response characteristics of virtual synchronous machines with different virtual inertias and damping coefficients
为了验证上述结论,图4(b)与(c)中给出了系统的频率响应,施加的扰动仍为t=1 s时投入一个有功负荷(等效于相位扰动)。从图4(b)中可以看出,系统在低惯量时(HVSG=0.2),频率超调变大而系统的阻尼特性变好(对应H2范数增大而H∞范数变小);系统在低阻尼时(D=5),频率超调变大且系统阻尼变差(对应H2与H∞范数均变大)。
从图4(c)中可以看出,系统在高惯量时(HVSG=10.0),频率超调变小而系统阻尼略微变差(对应H2范数变小而H∞范数增大);系统在高阻尼时,频率超调变小且系统阻尼变好(对应H2与H∞范数均变小)。总的来说,增大虚拟惯量HVSG和电气阻尼D均有利于提高虚拟同步机的频率扰动抑制能力,且GVSG(s)的H2与H∞范数可以有效地刻画系统的频率响应特性。
3 多机系统的频率响应特性
前两节通过单机无穷大系统,验证了相位扰动到频率输出闭环传递函数的H2与H∞范数可用于定量评价系统的频率响应特性,从而指导虚拟同步机的虚拟惯量与电气阻尼配置。
一方面,增大虚拟惯量或者电气阻尼可以抑制系统的频率波动,提高系统的频率稳定性;另一方面,增大虚拟惯量或者阻尼系数提高了逆变器在频率波动时的有功支撑能力,从而增加了投资,因为有功支撑能力的增加是以增加储能(电池、电容或旋转惯量等)为前提的[26-27]。因此,需要关注的是:在可配置的虚拟惯量(或有功支撑能力)一定时,如何在多台设备之间合理分配虚拟惯量,使得系统呈现出最优的频率扰动抑制能力。本文所采用的H2与H∞范数为解决这一问题提供了定量的衡量标准。
考虑如图5(a)所示的两区系统,同步发电机1与虚拟同步机1经线路对负荷1供电,同步发电机2与虚拟同步机2经线路对负荷2供电,两区域间经线路5相连。4台机组容量相同。

图5 两区系统的频率响应特性Fig.5 Frequency response characteristics of two-area system
两台同步发电机的惯量时间常数为:HSG1=4.0,HSG2=4.0,线路1至4的阻抗均为Z=0.003 5+j0.05(标幺值),线路5的阻抗为Z5=0.008+j0.15(标幺值)。选择系统输出为各同步机与虚拟同步机的频率,即
(15)
式中:ΔωSG1和ΔωSG2分别为同步发电机1与2的频率与其基准值(即2πf0)之差;ΔωVSG1和ΔωVSG2分别为虚拟同步机1与2的频率与其基准值之差。
系统输入为施加于各台同步机与虚拟同步机的相位扰动,表示为:
(16)
将整个系统在平衡点处线性化并求取其闭环传递函数矩阵可得:
y=Gsys(s)u
(17)
假定虚拟同步机1的惯量HVSG1与虚拟同步机2的惯量HVSG2总和不变,且HVSG1+HVSG2=8(标幺值)。图5(b)给出了Gsys(s)的H2与H∞范数随HVSG1变化而变化的曲线。可以看出,其H2与H∞范数随着电气阻尼D1与D2的增大而减小。当D1与D2恒定时,H2范数随HVSG1的变化而变化,且在HVSG1=HVSG2时有最小值。而在H∞范数HVSG1=HVSG2时有最大值,但考虑到H∞范数随HVSG1变化较小且主要与系统阻尼相关,因此可以认为HVSG1=HVSG2时该两区系统具有最优的频率扰动抑制能力。需要注意的是,Gsys(s)的H2与H∞范数是对其所有方向上的扰动抑制能力的综合度量,而并非只反映了某一特定方向上的扰动抑制能力。
为了验证上述H2与H∞范数分析得到的结论,附录A图A1给出了该四机系统的时域仿真波形。为了研究系统频率在不同扰动输入方向上的响应特性,t=1 s时在ΔuSG1施加阶跃扰动,t=11 s时在ΔuVSG1施加阶跃扰动,t=21 s时在ΔuSG2施加阶跃扰动,t=31 s时在ΔuVSG2施加阶跃扰动。这里选取4台机组频率偏差的二范数来反映系统的频率波动,即
(18)
当机组容量不同时,式(18)中的各偏差量还应根据机组容量进行加权。
从附录A图A1中可以看出,算例1系统的频率波动明显大于算例2与算例3,也就是说,该系统的频率扰动抑制能力在HVSG1=HVSG2时优于HVSG1≠HVSG2。对比算例2与算例3可知,随着阻尼系数D1与D2的增大,系统在ΔuVSG1与ΔuVSG2方向上的扰动抑制能力明显增强,即电气阻尼的合理配置可以提高系统的频率响应特性。上述仿真结果与图5(b)的H2与H∞范数分析结果一致。图5(b)左侧图满足HVSG1+HVSG2=8,D1=D2=4;右侧图满足HVSG1+HVSG2=8,D1=D2=20。
上述结论是在线路1至4的阻抗均相等时得出的,事实上,当线路阻抗发生变化时,系统的频率特性也会随着发生变化。假设线路1至3的阻抗仍为Z=0.003 5+j0.05,而线路4的阻抗变化为Z4=0.003 5+j0.5,图5(c)给出了此时系统的H2与H∞范数随HVSG1变化而变化的曲线。图5(c)左侧图满足HVSG1+HVSG2=8,D1=D2=4;右侧图满足HVSG1+HVSG2=8,D1=D2=20。可以看出,系统的H2与H∞范数曲线不再呈左右对称,且H2范数的最小值出现在HVSG1/(HVSG1+HVSG2)≈0.6附近,考虑到H∞范数随HVSG1变化不大,则此时系统具有最优的频率响应特性。可见,系统中虚拟惯量的优化配置与系统的网架结构(线路参数等)有关。
为了验证上述结论,附录A图A2给出了|Δω|2的时域仿真波形,可以看出,算例 3下的系统频率波动明显小于算例1与算例2。算例1与算例2具有不同的频率响应特性,且算例1下频率波动更大。上述仿真结果与图5(c)的H2与H∞范数分析结果一致,验证了以Gsys(s)的H2与H∞范数刻画多机系统频率响应特性的有效性。
4 结语
以H2与H∞范数为指标定量分析了同步发电机与虚拟同步机的频率响应特性,探讨了虚拟同步机的虚拟惯量与电气阻尼配置问题。研究表明:①相位扰动到频率输出闭环传递函数(或传递函数矩阵)的H2与H∞范数可以有效地刻画含虚拟惯量的电力系统的频率响应特性,并为虚拟惯量在多虚拟同步机系统中的优化配置提供定量的评价指标;②通过合理配置虚拟惯量与电气阻尼可以使虚拟同步机的频率响应特性优于同步发电机;③虚拟惯量在电力系统中的优化配置与网架结构、线路参数等相关。
后续研究工作中,亦可以将该指标用于分析基于锁相环的电力电子设备的大规模应用对于电力系统频率响应特性的影响。
本文受到云南电网有限责任公司科技项目(yndw(2016)000303DD00124)资助,特此感谢。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
参考文献
[1] 袁小明,程时杰,胡家兵.电力电子化电力系统多尺度电压功角动态稳定问题[J].电机工程学报,2016,36(19):5145-5154.
YUAN Xiaoming, CHENG Shijie, HU Jiabing. Multi-time scale voltage and power angle dynamics in power electronics dominated large power systems[J]. Proceedings of the CSEE, 2016, 36(19): 5145-5154.
[2] 郑天文,陈来军,陈天一,等.虚拟同步发电机技术及展望[J].电力系统自动化,2015,39(21):165-175.DOI:10.7500/AEPS20150508006.
ZHENG Tianwen, CHEN Laijun, CHEN Tianyi, et al. Review and prospect of virtual synchronous generator technologies[J]. Automation of Electric Power Systems, 2015, 39(21): 165-175. DOI: 10.7500/AEPS20150508006.
[3] 胡泽春,丁华杰,宋永华,等.能源互联网背景下储能应用的研究现状与展望[J].电力建设,2016,37(8):8-17.
HU Zechun, DING Huajie, SONG Yonghua, et al. Research status and prospect of energy storage application under energy internet background[J]. Electric Power Construction, 2016, 37(8): 8-17.
[4] 程冲,杨欢,曾正,等.虚拟同步发电机的转子惯量自适应控制方法[J].电力系统自动化,2015,39(19):82-89.DOI:10.7500/AEPS20141130003.
CHENG Chong, YANG Huan, ZENG Zheng, et al. Rotor inertia adaptive control method of VSG[J]. Automation of Electric Power Systems, 2015, 39(19): 82-89. DOI: 10.7500/AEPS20141130003.
[5] HE W, YUAN X M, HU J B. Inertia provision and estimation of PLL-based DFIG wind turbines[J]. IEEE Transactions on Power Systems, 2017, 32(1): 510-521.
[6] CARDENAS R, PENA R, ALEPUZ S, et al. Overview of control systems for the operation of DFIGs in wind energy applications[J]. IEEE Transactions on Industrial Electronics, 2013, 60(7): 2776-2798.
[7] 丁明,杨向真,苏建徽.基于虚拟同步发电机思想的微电网逆变电源控制策略[J].电力系统自动化,2009,33(8):89-93.
DING Ming, YANG Xiangzhen, SU Jianhui. Control strategies of inverters based on virtual synchronous generator in a microgrid[J]. Automation of Electric Power Systems, 2009, 33(8): 89-93.
[8] ZHONG Q C, WEISS G. Synchronverters: inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.
[9] D’ARCO S, SUUL J A, FOSSO O B. A virtual synchronous machine implementation for distributed control of power converters in smart grids[J]. Electric Power Systems Research, 2015, 122: 180-197.
[10] 吕志鹏,盛万兴,钟庆昌,等.虚拟同步发电机及其在微电网中的应用[J].中国电机工程学报,2014,34(16):2591-2603.
LÜ Zhipeng, SHENG Wanxing, ZHONG Qingchang, et al. Virtual synchronous generator and its applications in micro-grid[J]. Proceedings of the CSEE, 2014, 34(16): 2591-2603.
[11] WANG Y, DELILLE G, BAYEM H, et al. High wind power penetration in isolated power systems—assessment of wind inertial and primary frequency responses[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2412-2420.
[12] 陈宇航,王刚,侍乔明,等.一种新型风电场虚拟惯量协同控制策略[J].电力系统自动化,2015,39(5):27-33.DOI:10.7500/AEPS20140212007.
CHEN Yuhang, WANG Gang, SHI Qiaoming, et al. A new coordinated virtual inertia control strategy for wind farms[J]. Automation of Electric Power Systems, 2015, 39(5): 27-33. DOI: 10.7500/AEPS20140212007.
[13] HUANG L B, XIN H H, ZHANG L Q, et al. Synchronization and frequency regulation of DFIG-based wind turbine generators with synchronized control[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 1251-1262.
[14] GONZALEZ-LONGATT F M. Impact of emulated inertia from wind power on under-frequency protection schemes of future power systems[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(2): 211-218.
[15] XIONG L S, ZHUO F, WANG F, et al. Static synchronous generator model: a new perspective to investigate dynamic characteristics and stability issues of grid-tied PWM inverter[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6264-6280.
[16] HU J B, WANG S, TANG W M, et al. Full-capacity wind turbine with inertial support by adjusting phase-locked loop response[J]. IET Renewable Power Generation, 2017, 11(1): 44-53.
[17] HUANG L B, XIN H H, WANG Z, et al. A virtual synchronous control for voltage source converters utilizing dynamics of DC-link capacitor to realize self-synchronization[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(4): 1565-1577.
[18] 王锡凡.现代电力系统分析[M].北京:科学出版社,2003.
[19] SIMPSON-PORCO J W, DÖRFLER F, BULLO F. Synchronization and power sharing for droop-controlled inverters in islanded microgrids[J]. Automatica, 2013, 49(9): 2603-2611.
[21] SKOGESTAD S, POSTLETHWAITE I. Multivariable feedback control[M]. New York: Wiley, 1996.
[22] 黄林彬,章雷其,辛焕海,等.下垂控制逆变器的虚拟功角稳定机理分析[J].电力系统自动化,2016,40(12):117-123.DOI:10.7500/AEPS20150709007.
HUANG Linbin, ZHANG Leiqi, XIN Huanhai, et al. Mechanism analysis of virtual power angle stability in droop-controlled inverters[J]. Automation of Electric Power Systems, 2016, 40(12): 117-123. DOI: 10.7500/AEPS20150709007.
[23] TAO Y, LIU Q W, DENG Y, et al. Analysis and mitigation of inverter output impedance impacts for distributed energy resource interface[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3563-3576.
[24] HE J, LI Y W, Analysis, design and implementation of virtual impedance for power electronics interfaced distributed generation[J]. IEEE Transactions on Industrial Application, 2011, 47(6): 2525-2538.
[26] 田新首,王伟胜,迟永宁,等.基于双馈风电机组有效储能的变参数虚拟惯量控制[J].电力系统自动化,2015,39(5):20-26.DOI:10.7500/AEPS20140320007.
TIAN Xinshou, WANG Weisheng, CHI Yongning, et al. Variable parameter virtual inertia control based on effective energy storage of DFIG-based wind turbines[J]. Automation of Electric Power Systems, 2015, 39(5): 20-26. DOI: 10.7500/AEPS20140320007.
[27] ZHU J, BOOTH C D, ADAM G P, et al. Inertia emulation control strategy for VSC-HVDC transmission systems[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1277-1287.

