库水位波动对石佛寺水库滑坡体稳定性的影响
韩东海
(桓仁县水务局,辽宁 桓仁 117200)
1 滑坡体发育特征
石佛寺水库是辽河干流上的一座河道型水库,坝址位于辽宁省沈阳市新城子区黄家乡,设计库容1.85亿m3,防洪库容1.60亿m3,控制流域面积16.5万km2[1]。2010年7月20日至21日,石佛寺水库坝址上游地区遭遇特大暴雨袭击,水库库区发生多出滑坡。其中,白沙滑坡位于水库右岸白沙段,滑坡宽约190m,面积5万m2,体积约80万m3。受2016年7月25日暴雨冲刷,滑坡变形有进一步加剧趋势。
石佛寺水库是一座典型的平原水库,库区边坡的地基特性是第四系覆盖[2]。滑坡体物质主要由第四系松散堆积物构成,其成因主要为坡积、人工堆积以及洪积。滑坡体按照组成成分可以分为上下两层:上层主要是碎石土和含碎石粘性土;下层主要是碎石土和孤石块体。滑坡体的地下水主要为基岩裂隙水,主要赋存于下部基岩中。对滑坡体滑带土取样进行室内试验,获得不同层位土体的物理力学参数,如表1所示。
2 数值模型的建立
2.1 方法选取
经过多年的研究和理论实践,目前形成了大量关于边坡稳定性的数值模拟软件,这些软件的理论基础和侧重点往往有所不同,用户要根据实际工程特点进行选择[3]。鉴于本次研究中的水位波动以及降雨对滑坡的影响过程十分复杂,且主要通过改变滑坡体的水动力场和岩土体的物理力学特性进而使

表1 采集样品的物理力学参数试验成果
滑坡体的稳定性发生改变。因此,模拟计算的首要任务是对不同工况下的滑坡渗流场的响应过程进行模拟,所以本文选取GeoStudio2007中的SEEP/W和SLOPE/W模块进行模拟计算[4]。具体计算思路是:首先在SEEP/W模块中设置计算边界条件,实现对降雨强度和水位升降等条件的模拟,然后导入基于渗流场模拟获得的孔隙水压力分布结果,进行两者之间的耦合分析,最终实现滑坡稳定性变化模拟结果[5]。
2.2 模型的概化
白沙滑坡地层自上而下可以分为碎石土、滑带土、次级滑动带和基岩,有限元概化模型如图1所示。
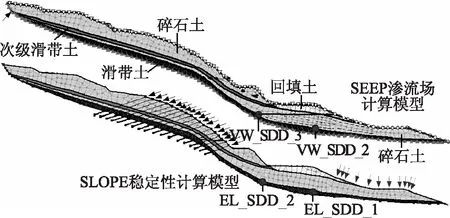
图1 有限元计算概化模型
3 渗流场模拟分析
3.1 计算原理
无论是库水位波动还是降雨渗入,水对滑坡体的影响本质上都属于饱和与非饱和状态相互转化的过程[6]。SEEP/W模块的理论基础是基于非饱和土体渗流的达西定律,在此模块中渗流系数随含水量及孔隙水压力的变化而变化,其二维渗流的控制方程为:
(1)
式中,Kx—水平方向饱和渗透系数;Ky—垂直方向饱和渗透系数;ρw—水的密度;mw—比水容量;g—重力加速度。
在计算之前首先要对概化后的滑坡连续体进行网格化离散,剖分类型选取为非结构化的四边形或三角形网格,共得到13245个网格单元,46547个节点。
3.2 计算边界
SEEP/W模型的边界条件主要是流量和水头边界[7]。由于野外实际条件下滑坡体的渗流边界十分复杂,在模型计算中需要对渗流边界进行必要的概化。基于上述原则,本次模型计算采用的边界条件为:假设滑坡体下部的基岩为不透水层,其与上部岩土体的接触面为0流量边界;滑坡体表面60m高程以下为石佛寺水库水位波动边界;滑坡体表面60m高程以上为降雨边界;低水位阶段的降雨和库水位上升模拟以55m静水位稳态分析结果为初始条件;库水位下降模拟则以60m水位稳态分析结果为初始条件。
3.3 参数的选取与校正
虽然在研究开始前通过取样试验获得了滑坡岩土体的物理力学参数,但是该滑坡体处于河道两侧,物质构成异常复杂,不同属性的岩土层空间分布极不均匀。因此,直接采用试验获取的数据,很难获得理想的模拟结果[8]。因此,基于试验数据,利用滑坡体地下水监测数据进行参数校正十分必要,校正后的参数见表2。利用滑坡中下部滑带部位孔隙水压力长期监测数据为依据,对流场模型进行反复优化,使优化后的模型模拟结果能较好符合滑坡体内渗流场变化情况。
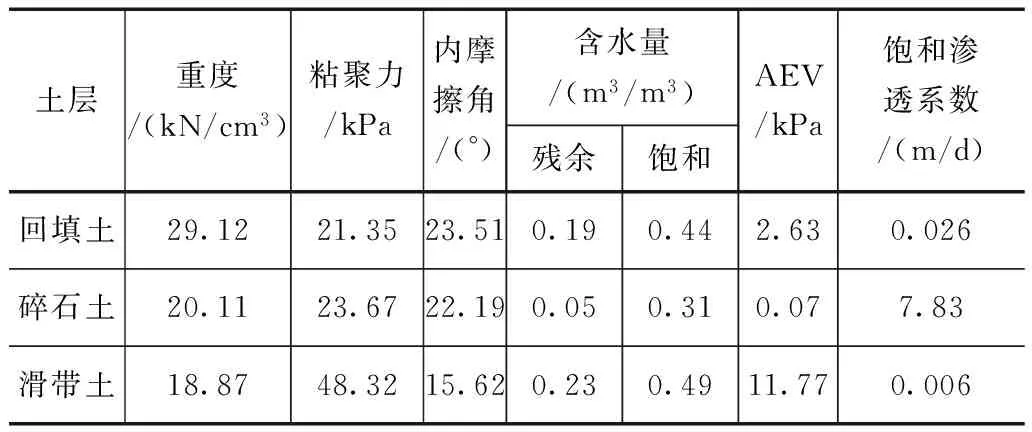
表2 校正后的岩土体物理力学参数
3.4 模拟工况的设定
石佛寺水库属于辽河干流上的调节性水库,在每个水文年中水库的水位在55~60m内涨落。考虑到沈阳地区汛期多短时强降雨,石佛寺水库库区水位升降速度较快,在模拟中设计稳态分析和瞬态分析两种工况,两种工况的具体参数如表3所示。

表3 稳定性模拟工况
4 库水位升降对滑坡稳定性的影响
众所周知,库水位升降速率是库区滑坡体变形的主要影响因素。汛期库水位升降变化速率较大的情况下,其对滑坡体内部渗流场的变化影响十分显著,从而对滑坡体的稳定性造成严重影响。对库水位升降速率进行模拟,探求库区不同水位、不同升降速率与滑坡体稳定性之间的响应关系,对研究水库型滑坡的成灾机理,预防和预测水库滑坡灾害具有重要意义。因此,基于上述模型,对表3中的两种不同工况下水位变化速率与滑坡稳定性之间的关系进行模拟计算,计算结果如图2、图3和表4所示。
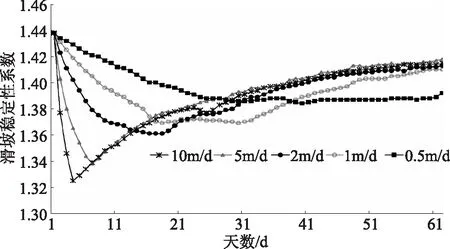
图3 工况2条件下不同速率下降过程中稳定性系数变化

水位变化速率稳定性达到极值的时间达到稳定装态所需的时间稳定性系数变化值升降升降升降0.5m/d606060590.0440.0461m/d313151590.0140.0262m/d161636590.0140.0265m/d7729590.0120.02110m/d3323560.0150.024
图2是工况1条件下库水位以不同速率上升过程中滑坡体稳定系数计算结果。计算结果显示,如果库水位上升速率大于1m/d,滑坡的稳定性先迅速增大,再缓慢减小,最后逐渐达到稳定状态;如果水位的上升速率小于1m/d,滑坡体的稳定性呈现出先减小再持续增大的变化趋势。由表4可知,工况1条件下当库水位上升速率大于1m/d时,滑坡体的稳定性系数的增大值为0.014左右,如果上升速率为0.5m/d时,这一数值为0.044。究其原因,在工况1条件下,如果库水以较大速率上升,则库水的静水压力有利于滑坡体保持稳定,其稳定性会持续增大;当水位稳定于60m后,库水会不断渗入滑坡体内部,并造成滑带部位的岩土体物理力学参数值减小,滑坡体的稳定性会逐步降低,并最终达到稳定状态。如果水位以较小速率上升,滑坡体会受到动、静水压力、浮托力以及岩土体的物理力学性质变化的共同影响,因此滑坡处于稳定阶段。
图3是工况2条件下,库水位以不同速率下降过程中滑坡体稳定系数计算结果。计算结果显示,当库水位下降速率大于1m/d时,滑坡体的稳定性变化趋势为先迅速减小,然后缓慢增大,最终达到稳定状态;当库水位下降速率小于1m/d时,滑坡体稳定性的变化趋势为先逐渐减小,然后缓慢增大,最终达到稳定状态。由表4的数据可知,库水位的下降速度越快,滑坡体稳定性达到最差的时间也就越短,而增大至稳定状态的时间变化并不明显。如果库水位下降速率大于1m/d时,当滑坡体达到稳定状态时的稳定性系数减小0.026,而库水位下降速率为0.5m/d时,这一数值为0.046。究其原因,当库水位下降速率较大时,对滑坡体的稳定性起主导作用的是静水压力,而随着库水位的不断降低,动水压力增大而静水压力减小,滑坡体的稳定性也将不断减小;当库水位降低到55m后,岩土体的物理力学参数开始对滑坡体的稳定性起主导作用,所以滑坡体的稳定性会随着岩土体的物理力学参数的增大而逐渐升高,并最终达到稳定状态。如果库水位下降速率较小,在水位下降的初始阶段起主导作用的是静水压力,所以滑坡体的稳定性缓慢降低到极值,而随着静水压力的不断减小,岩土体参数逐渐增大并开始起主导作用,所以滑坡的稳定性逐渐增大,并达到稳定状态,因而在整个库水位下降过程中,滑坡体均处于稳定阶段。
5 结语
本文以石佛寺水库库区白沙滑坡稳定性为研究对象,利用有限元分析软件,结合长期的地质观测数据,对库水位波动过程中滑坡体内部的渗流场变化规律进行了分析。研究结论显示白沙滑坡处于蠕滑状态,滑坡变形主要集中于石佛寺水库水位下降阶段,短期内并不会诱发严重的地质灾害和次生灾害。但是,白沙滑坡体的变形会对附近的明沈公路以及部分建筑产生潜在影响,建议水库管理部门和当地国土部门在水库水位下降期要加大监测密度,及时掌握滑坡体的变形动态,及时对其变形趋势进行合理判别和处置。
[1] 董福君. 石佛寺水库地下水监测系统的应用与成果分析[J]. 水利建设与管理, 2012(12): 63- 65.
[2] 赵鑫. 石佛寺水库生态修复若干问题及对策[J]. 水利规划与设计, 2015(11): 22- 23+37.
[3] Thielen, A, Springman, SM. Predicting the variation of stability with time for a Slope in Switzerland slope in[J]. In: Ist European Conference on Unsaturated Soils. 2008: 941- 946.
[4] 张玉, 徐卫亚, 邹丽芳, 孙怀昆. 降雨条件下大型滑坡体渗流稳定性分析[J]. 岩土力学, 2013, 03: 833- 841.
[5] Timpong S, ItohK, Toyosawa Y. Geotechnical centrifuge modeling of slope failure induced by ground water table change[C]. Landslides and Climate Change [A]. London: Taylorand Francis Croup, 2007, 107- 112.
[6] WANG Fa-wu, ZHANG Ye-ming, HUO Zhi-tao, et al. Movement of the Shuping landslide in the first four years after the initial impoundment of the Three Gorges Dam Reservoir, China[J]. Landslides, 2008, 5(3): 321- 329.
[7] 雷远见. 乐昌峡水利枢纽库水位下降对鹅公带滑坡体稳定性的影响[J]. 黑龙江水利科技, 2013(06): 116- 118.
[8] 梁学战, 陈洪凯. 库水位升降条件下不同渗透性的滑坡体稳定性变化规律[J]. 中国地质灾害与防治学报, 2012(04): 20- 26.

