不同工况下梯级土石坝溃决模型对比研究
赵 丹
(抚顺县水利水电工程移民局,辽宁 抚顺 113118)
在我国已建的大坝中,土石坝占据着重要的地位,其数量约93%左右,发生溃坝事故的概率较大[1]。国内外在对不同工况下的梯级土石坝溃坝问题的研究较少,因此运用数值模拟的方法对其进行风险分析及机制的研究具有积极的现实意义。目前,国内外在对土石坝的数值模拟研究中,所建立的溃坝模型主要包括参数模型及机理模型两类。Vridud等通过试验研究认为剪应力和侵蚀率的关系在特定的状态下存在一定的线性关系[2]。在对土石坝的溃坝模型试验研究中,主要涉及溃坝洪水及溃坝机理的研究。邵东琛分析了坝体的上游坡度、所用材料的微观粒径及坝高等因素,对不同工况下的溃坝过程进行了研究,分析并总结了该坝体溃决的规律[3]。江德军在利用相关水槽的试验中对梯级土石坝的连续溃决过程进行了研究[4]。
本文以上寺水库为例进行土石坝溃决模型对比研究。上寺水库位于浑河支流莲岛河中游,坝址以上流域面积48km2,河道平均比降6‰,浑河流域北高南低,最高海拔295m。上寺水库为小(1)型水库,设计洪水标准为50年一遇。水库土石坝为粘土心墙坝,高程为145m,防浪墙为1.8m,坝顶宽度为60m,溢洪道净宽度为36m,最大泄洪量720m3/s。考虑到该土石坝存在一定风险,于2014年7月进行人工开挖泄洪,泄洪槽深为12m,坡度1∶1.5,泄洪当日12时,下泄最大流量达到647m3/s,水位自142.3m下降至118.6m,至次日8时完成泄洪过程,整个过程的参数均有数据记录,为本文的研究提供了较好的基础条件。
1 土石坝溃决模型的对比分析
在对水库的梯级土石坝溃决模型研究中,溃坝模型主要包括机理模型和参数模型两类。
(1)Hec-Ras模型,是针对一维恒定流、非恒定流的水力模型,主要包括河水泥沙的沉积计算、模拟恒定流动态及对水质的测定分析等功能[3]。其中,对于大坝采用Inline Structure功能进行描述,对坝体的参数进行设置等。
(2)Dambrk模型,是一维非恒定流动力演算的溃坝洪水模型。该模式主要包括管涌及漫顶损坏两种,在漫顶破坏模式下,该模型最为常用。
(3)Mike21 HD模型。Mike21可以模拟河流、湖泊、河口、海湾、海岸及海洋的水流、波浪、泥沙及环境,其中的水动力模块(HD)可以模拟湖泊、河口和海岸地区的水位变化及由于各种力的作用而产生的水流变化,可以求解动态流的连续方程和动量守衡方程,本文主要采用能量方程法对溃坝模型进行研究。
(4)堰塞坝溃决参数快速评估模型。该模型主要根据大量的数据统计分析建立的模型数据库。可以从与坝体相关的一些物理参数中计算出大坝的溃决数据。表1为典型堰塞坝案例的计算结果。
(5)Breach模型。该模型是1997年开发的一种针对溃坝问题的软件计算模型,目前已运用到很多现实案例中[5]。并且,对于坝体的要求简单,在目前的梯级土石坝模型中应用很广。

表1 典型堰塞坝案例计算结果
(6)Db-Iwhr模型。该模型是2015年开发的一种针对溃坝问题的计算模型,包括对堤坝溃口的垂直侵蚀、堤坝溃口的流水速率、堤坝溃口的横向扩张等进行了详细的计算[6]。计算方法较简便,计算结果准确且精度较高。
2 试验结果与分析
由相关文献记载,该水库大坝存在着溃决的风险。本文通过利用各种影响因素进行综合分析,采用六种模型对辽宁上寺水库大坝参数进行统计及分析,在获取相关数据的基础上得出对比分析的结果。
2.1 Hec-Ras模型输入参数及计算结果
采用Hec-Ras软件模型对上寺水库大坝溃决过程进行数值模拟分析,其中需要输入的物性参数见表2。

表2 Hec-Ras模型所利用的计算参数
计算的结果指标主要有堤坝溃口处水的流量及水库中水位的变化,其变化过程见图1所示。

图1 水库中水位的计算值与实测值曲线
该Hec-Ras软件模型中没有计算溃口的特有方程公式,因此需要预先在软件模型建立时设置好堤坝溃口的时序变化程序。该计算结果受到影响的因素较多,对堤坝溃口的宽度、深度、水库的流速等信息参数不能得到计算结果[7]。
2.2 Dambreak模型输入参数及计算结果
模拟了上寺堰塞坝爆发过程,计算结果包括堤坝中水量的流量线、溃坝口水量的流量线,溃坝口的底部宽度变化及水库中水流的流速变化等。水库中水位的计算值与实测值曲线具体如图2所示,计算模拟的溃坝口水流量与实际流量曲线如图3所示,计算模拟的溃坝口水流速与实际流速曲线如图4所示。
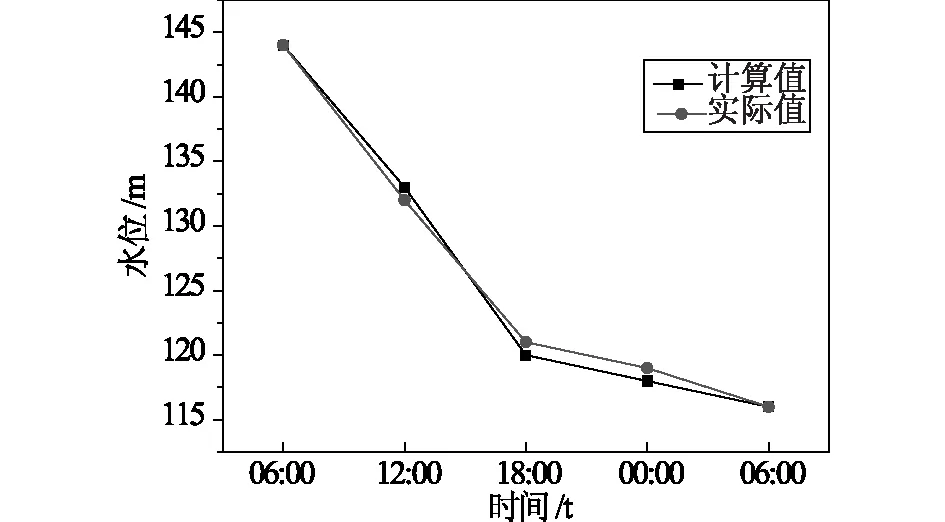
图2 水库中水位的计算值与实测值曲线
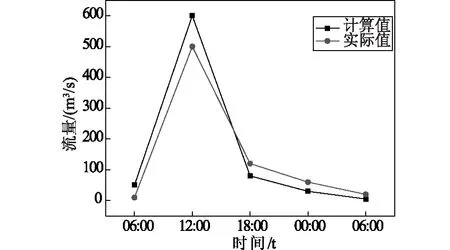
图3 计算模拟的溃坝口水流量与实际流量曲线

模型类别体积V1宽度W高度H水库容积V2β1β2β3β4β5三参数模型全参数模型21.09622.384321-0.724-1.762-1.8130.714-0.6590.661-1.896-87.210.671-2.802
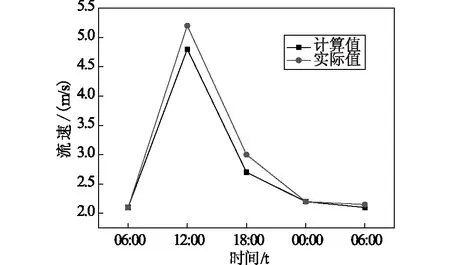
图4 计算模拟溃坝口水流速与实际流速曲线
2.3 Mike21 HD模型输入参数及计算结果
利用Mike21 HD模型对上寺水库大坝溃决过程进行数值模拟分析,输入物性参数见表3。

表3 Mike21 HD模型所用的主要输入参数
计算结果主要有堤坝溃口底部高程、堤坝溃口水面的宽度、堤坝溃口的流量、水库中水的流速及水位等。水库中水位的计算值与实测值曲线如图5所示,堤坝溃口底部高程的计算值与实测值曲线如图6所示。

图5 水库中水位的计算值与实测值曲线

图6 堤坝溃口底部高程的计算值与实测值曲线
结果显示,通过利用该模型计算出来的最大洪水流量为672.5m3/s,与实际值的误差为6.1%,洪水出现的时间节点和实际值比较接近。堤坝溃口的底部高程、水库水位和实际测量值相差不大[8]。但是,堤坝溃口水面的宽度值则与实际值偏差较大,原因在于Mike21 HD模型没有充分考虑溃口侧面的石壁损坏情况,导致计算出的数值不能准确的表示出其变化的趋势。
2.4 溃决参数快速评估模型输入参数及计算结果
利用三参数模型和全参数模型对上寺水库大坝溃决过程进行数值模拟分析,需要利用的输入物性参数见表4。
计算结果主要有堤坝溃决时间、溃口的最终底部宽度、溃口最终的顶部宽度、溃口最终的深度及溃坝洪峰流量等,见表5。

表5 水库大坝溃决过程计算结果
从表4中可以看出,利用全参数模型计算的数值较三参数模型更加准确。其中,峰值流量的计算结果与实际数值相差不大,相对误差小于1%。计算的堤坝溃决时间和实际数值相差2.5h。在堤坝的溃口参数计算中,溃口最终的深度值和顶部宽度值相比其他参数指标而言没有过大的偏差,溃口的最终底部宽度值在两个参数模型中相差较大[9]。
2.5 Breach模型输入参数及计算结果
利用Breach模型对上寺水库大坝溃决过程进行数值模拟分析[10]。输入物性参数见表6。
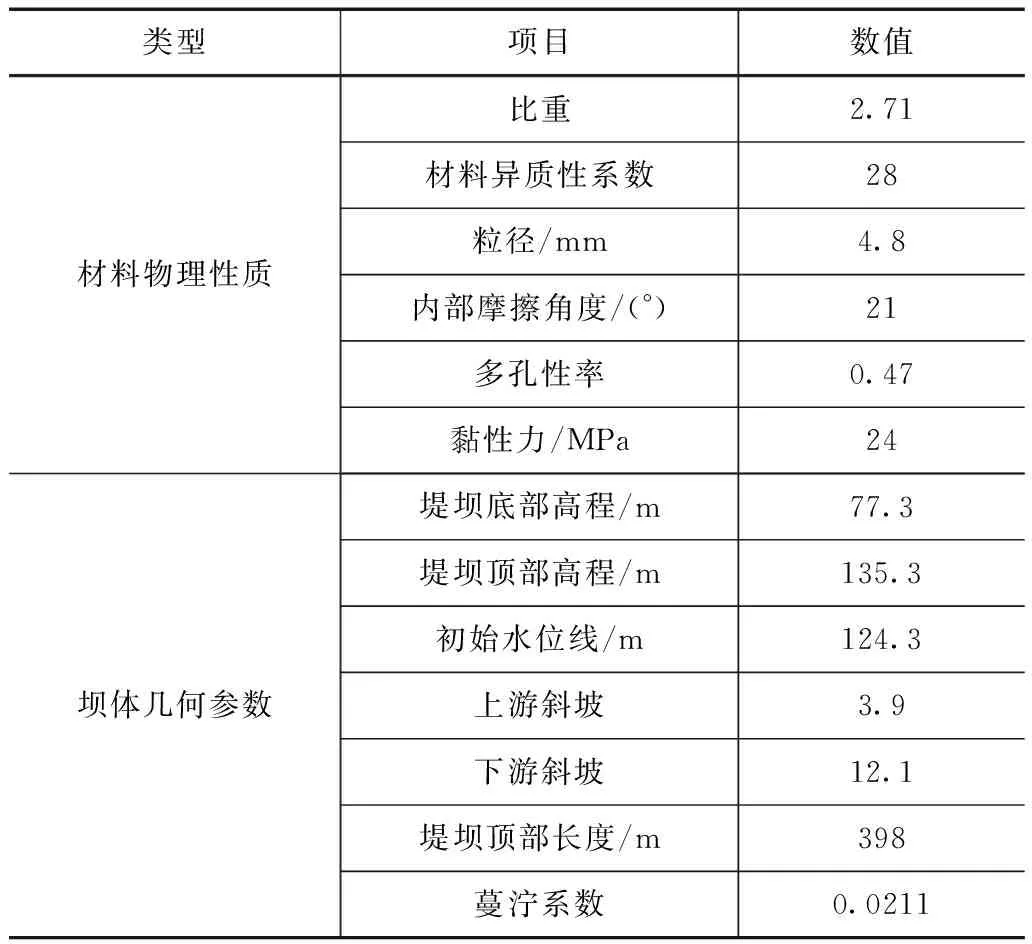
表6 Breach模型的主要输入参数
计算结果主要有堤坝口底部高度及宽度变化过程、水库水位线的控制及堤坝口水流量控制线等。水库水位的计算值与实测值曲线见图7,堤坝溃口底部高程的计算值与实测值曲线见图8。

图7 水库中水位的计算值与实测值曲线

图8 堤坝溃口底部高程的计算值与实测值曲线
用Breach模型对整个堤坝溃坝过程进行了比较完整的计算和分析,不过仍存在一些计算过程复杂、不确定性因素较多的问题。结果显示,该模型计算出的溃口流量为635.2m3/s,溃口流量和出现的时间与实际值有较大偏差。同时还可以看出,堤坝口底部高度、水库水位值与实际测定情况相比有些许不同,并且呈现不断降低的趋势,而且堤坝口底部宽度的变化形式与实际情况的很大相同之处,就是在数值上有比较大的偏差。
2.6 Db-Iwhr模型输入参数及计算结果
利用Db-Iwhr模型对上寺水库大坝溃决过程进行数值模拟分析,输入物性参数见表7。

表7 Db-Iwhr模型的主要输入参数
计算结果主要有堤坝口底部高度及宽度变化过程、水库水位线的控制、水库水流速及堤坝口处水流量的控制线等。水库水位计算值与实测值曲线见图9,堤坝溃口底部高程的计算值与实测值对比见图10。
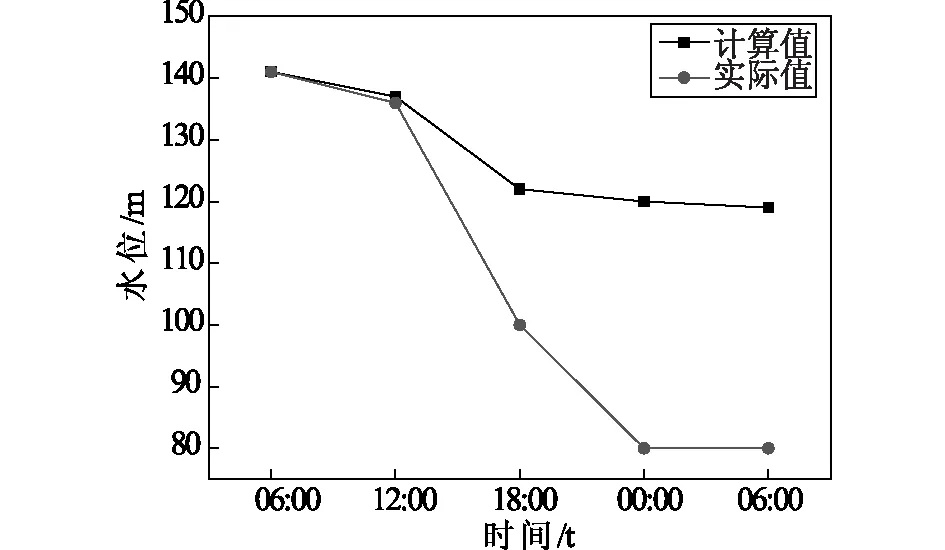
图9 水库中水位的计算值与实测值曲线
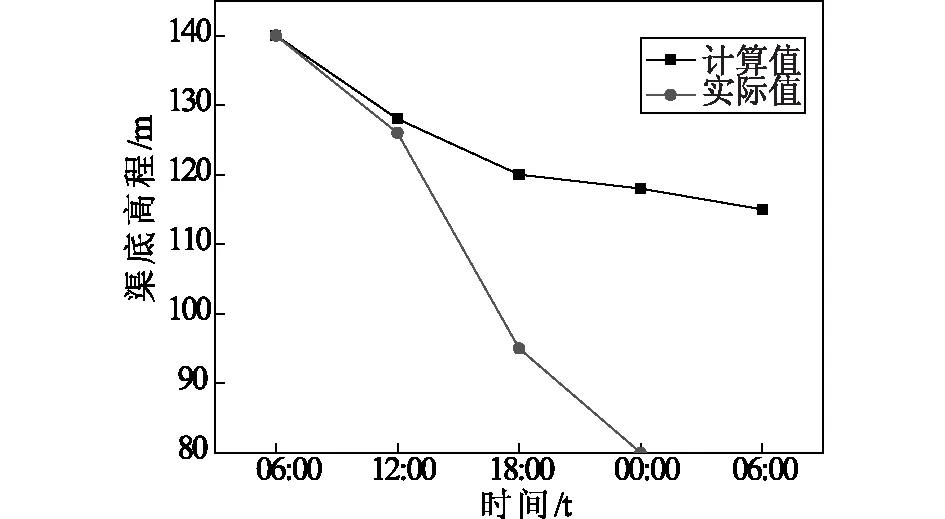
图10 堤坝溃口底部高程的计算值与实测值曲线
Db-Iwhr模型与其他几种模型的不同之处,主要在于不需要对溃坝的初始及最终尺寸参数进行设置,运用相关的理论可以对其现实的堤坝进行模拟计算得出结果。结果显示,模拟计算的溃坝洪峰水流量为752.8m3/s,和实际值相差不大。且计算的流量变化曲线和实际的情况比较相一致,仅水流量数值略显偏大。流速变化基本与实际情况一致,最大速度6.25m/s,接近测量值6.14m/s。峰值流量过后,测得的储层水位和河道底部高程缓慢降低,直到恒定。模拟值显示持续下降,是因为模型未考虑坝断裂过程后期的砂沉积。在达到突破宽度测量值的高峰后迅速下降,达到最大值后模拟破裂宽度保持不变。
3 结论
以上寺水库的大坝溃决问题为研究对象,分别采用了Hec-Ras、Dambrk、Mike21 HD、Breach、Db-Iwhr以及溃决参数快速评估等六种模型对不同工况下的梯级土石坝连溃过程进行数值模拟分析,并着重比较了每个模型的计算准确性。根据计算精度,最终选取Db-Iwhr模型作为土石坝溃决的计算模型。本文研究结果对梯级土石坝溃决模型选择具有一定应用价值。
[1] 纪伟. 某均质土石坝防渗加固设计与渗流数值模拟研究[J]. 水利规划与设计, 2017(09): 76- 78.
[2] 王多姿. 土石坝应急修复土料碾压遍数确定方法[J]. 水利技术监督, 2017, 25(04): 10- 11.
[3] 邵东琛. 一种改进邓肯张模型及其在土石坝数值模拟中的应用[J]. 三峡大学学报(自然科学版), 2015, 37(04): 21- 24.
[4] 江德军, 黄会宝, 柯虎, 等. 土石坝填筑数值模拟中分层数影响研究[J]. 人民长江, 2015, 46(S1): 130- 131+136.
[5] 汤开宇, 王乐华, 龚家伟, 等. 基于数值模拟分析的土石坝泄洪与蓄水过程安全预测[J]. 水利水电技术, 2015, 46(01): 99- 102.
[6] 张强, 刘慧娟, 李文柱, 等. 有限元分析在高烈度地区土石坝设计中的应用[J]. 水利规划与设计, 2015(09): 81- 85.
[7] 李红娜. 土石坝沥青混凝土防渗心墙的施工技术及质量控制[J]. 水利技术监督, 2014, 22(02): 8- 10.
[8] 哈丽木热木·阿布都热西提, 侍克斌, 李玉建. 非均质无限深透水地基上土石坝微透水防渗墙的有限元渗流计算[J]. 水资源与水工程学报, 2013, 24(06): 88- 91.
[9] 魏海云, 龚宇平, 李春贵. 桐柏抽水蓄能电站土石坝渗流监测及模拟分析[J]. 浙江水利科技, 2009(03): 16- 18+21.
[10] 周兴波, 陈祖煜, 黄跃飞, 等. 特高坝及梯级水库群设计安全标准研究Ⅲ: 梯级土石坝连溃风险分析[J]. 水利学报, 2015, 46(07): 765- 772.

