双排桩支护结构的数值模拟分析

李 力

(武汉地产开发投资集团有限公司，武汉 430022)

基坑支护工程是一项复杂的综合工程，虽然属于临时性工程，但是其技术复杂性却难于一般永久性的上部结构，稍有疏忽就可能导致基坑垮塌，造成人员伤亡。为保证深基坑施工安全、周围环境不受到损害、基坑周边建(构)筑物的安全以及地下主体结构施工所需要的足够空间，应该采取合理的支护结构形式[1]。随着现代工程的发展需要，基坑的发展也带来了许多变化，基坑支护工程的围护结构也变得多元化。支护结构的设计使用年限应不小于1年[2]。其中双排桩门架式支护形式是一种较为理想的支护方式[3]。双排桩门架式支护结构可以在不设置内支撑的条件下，依然发挥出其空间效应，并且能与桩间土协同作用，来平衡因基坑开挖所引起的内力，从而保持基坑边坡的稳定，良好的控制位移，达到施工与环境相协调的目标[4]。

1 FLAC计算模型的建立

FLAC是一种可以完成拉格朗日分析的显示有限差分程序，其全称是：Fast Lagrangian Analysis of Continua，是美国的Itasca公司开发和研究的力学分析软件。FLAC计算软件分为2D和3D两个版本，FLAC3D作为FLAC2D的升级版，是将平面问题向三维空间问题转化的方法，可用于模拟分析岩石、土质和其他材料的三维力学特性。

1.1 工程概况

该基坑周长约568.0 m，面积约19 000.0 m2。建筑物层次：地上4～49层、地下2～3层。各土层力学参数详见表1。

工程采用相对标高，相对标高±0.00=22.65 m。基坑开挖深度-12.70～-20.40 m,桩顶放坡2.5 m,坡比1∶1.0。支护桩采用钻孔灌注桩φ1 000@1 400，L=24 m，自然地面标高为-2.250 m，桩顶位于-4.75 m；双排桩桩身、桩顶冠梁及斜支撑均采用C30等级混凝土，冠梁为1 200 mm×800 mm，支撑设置在桩顶冠梁上，尺寸为600 mm×800 mm，弹性模量为30 GPa，其水平刚度系数为30 000 kN/m。

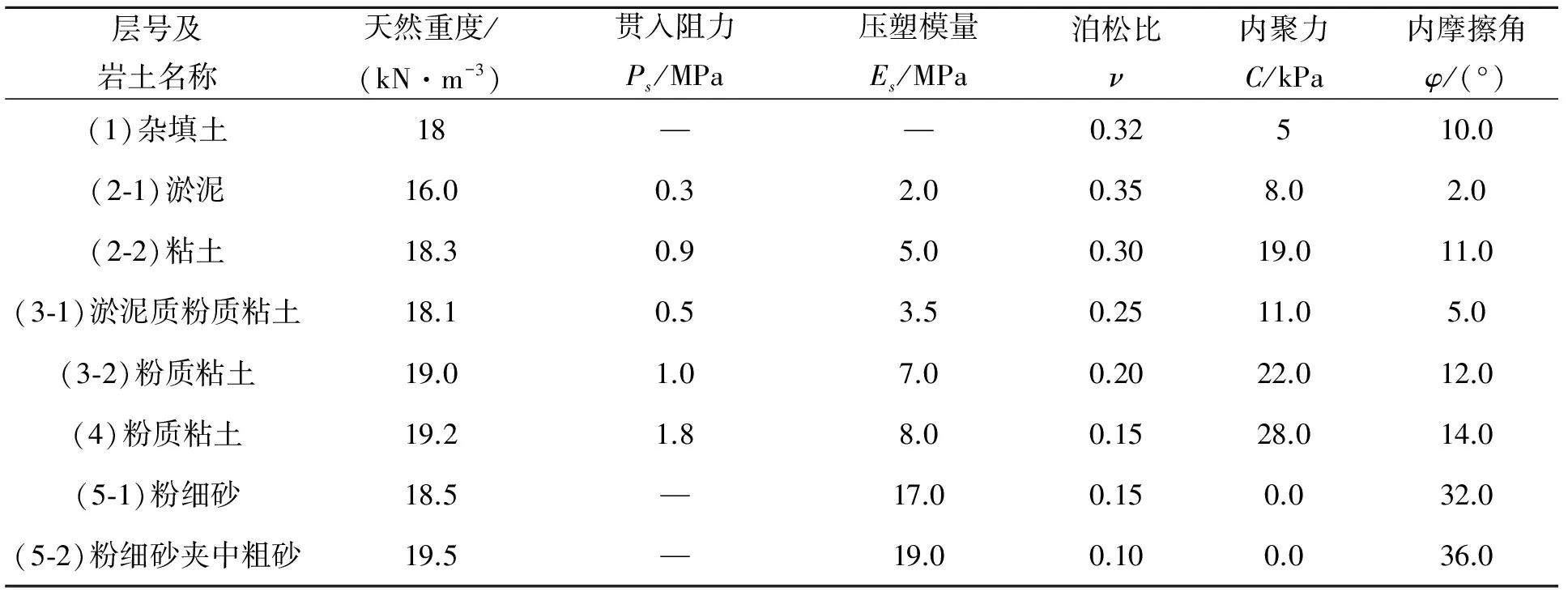
表1 土层物理力学参数

1.2 计算模型的基本参数

FLAC3D中提供了11种本构模型。土体的粘聚力和内摩擦角的取值详见表1，抗拉强度均假设为零。桩体以及土体单元均采用实体单元，桩单元、连梁及土体均视为线弹性体，并在连梁与土体的交界面插入一无厚度的接触面，即屈服条件采用摩尔—库伦屈服准则的“interface”单元。土体的剪切模量G和体积模量K的计算公式如下

(1)

(2)

其中,E为土体的弹性模量;υ为土体的泊松比。各土层的弹性模量和泊松比由勘察单位现场试验数据所得，土层的体积模量K和剪切模量G计算结果见表2。

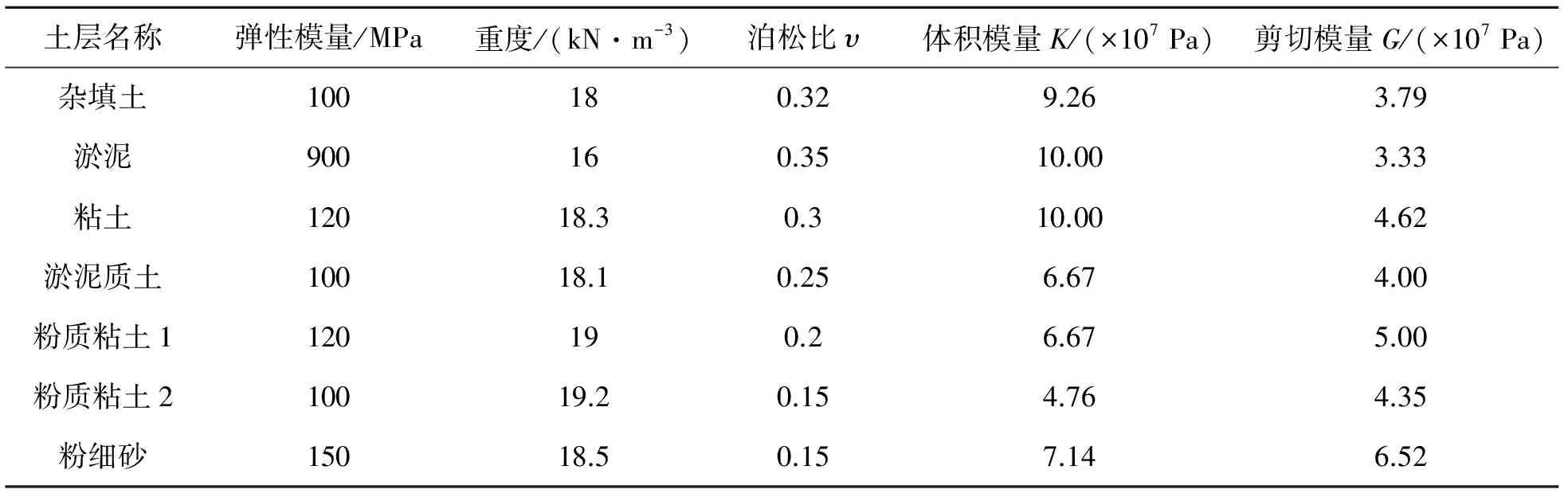
表2 土层K、G取值

1.3 计算模型简介

在基本参数和假定下，此模型结合工程实际情况进行单元网格划分，前、后排桩均采用实体单元建模，前、后桩排距3 m，桩间距1.5 m，桩径1 m，嵌固深度16 m，模型尺寸长48 m，高40 m，宽1.5 m(即桩间距)，以前排桩桩顶为坐标原点，模型共计11 736个单元，单桩模型864个单元。模型建立后，通过FLAC3D数值模拟得到双排桩的水平位移图。

由图1可以知道，模型当中最大的位移处于前排桩桩顶，桩顶部的位移为50.59 mm，相当于实测值的1.7倍，桩底部分位移趋近于零，桩身位移的分布曲线与土体的位移趋势基本相同，符合实际情况。在桩身不破损的情况下，可采用公式(3)～式(5)计算桩身弯矩。

(3)

(4)

Δε=ε+-ε-

(5)

式中，σ+、σ-分别是在同一截面的拉、压应力，Pa；ε+、ε-分别表示在同一截面的拉、压应变；EI表示桩的抗弯刚度，N·m2；b0表示在同一截面测点距离，m。弯矩如图2所示。

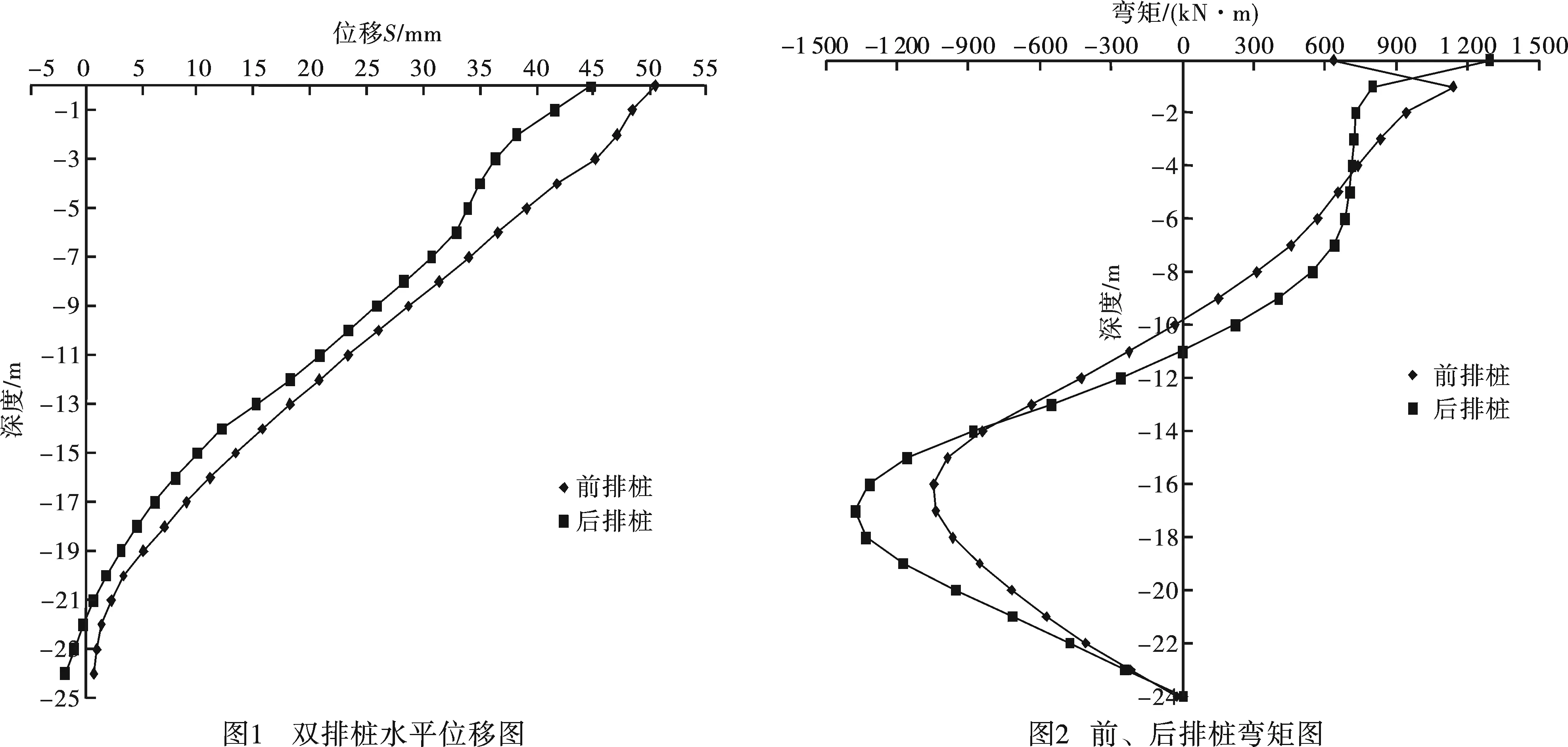
从图2中可知，前、后排桩均为坑底以上迎土面受拉，坑底以下挖土面受拉，随着土体的加深，前后排桩的弯矩中，后排桩最大弯矩值大于前排桩最大弯矩值，桩顶弯矩存在突变，可能是由于连梁的应力集中带来的变化，反弯点位置在桩身10 m左右，双排桩桩身弯矩趋势呈“S”型，符合实际情况。

2 连梁刚度对结果影响分析

实际工程中，连梁宽度部分通常采用整板浇筑，因此通过改变连梁的高度达到改变其刚度的目的。保持连梁的宽度1 200 mm不变，高度范围在600～1 200 mm之间，得到弯矩图及位移图。

改变连梁高度得到弯矩和位移曲线见图3、图4，由图可知，改变连梁刚度，在刚度较小时，前排桩桩顶位移大于后排桩桩顶位移，且差距较大，后排桩最大弯矩大于前排桩；逐渐增加连梁刚度，前排桩的最大位移急剧减小，最大弯矩平稳降低，后排桩最大位移减小效果不如前排桩，最大弯矩逐渐增大。适当的增大连梁的刚度，双排桩门架式支护结构的空间协调能力能得到提升，然而随着连梁刚度的增大，虽然使得桩体变形越来越小，但是也导致了后排桩弯矩的增大，因此，不能为达到减少变形的目的过于增大连梁的刚度。采用增加连梁刚度的效果并不是特别实用，实际设计过程中，应该适量增大连梁刚度，使得位移在控制范围内，且桩身的内力能保持尽量小。

3 结 论

a.运用FLAC数值模拟软件对该工程进行模拟计算，土拱作用效应比较明显，双排桩桩身弯矩趋势呈“S”型，符合实际情况，因此建立的计算模型是比较合理的。

b.适当地增大连梁的刚度，双排桩门架式支护结构的空间协调能力能得到提升，然而随着连梁刚度的增大，虽然使得桩体变形越来越小，但是也导致了后排桩弯矩的增大，因此，不能为达到减少变形的目的过于增大连梁的刚度。在设计过程中，在控制变形的情况下使桩身所受内力最小，达到经济安全的目标。

[1] 何颐华，杨 斌，金宝森,等.双排护坡桩试验与计算的研究[J].建筑结构学报，1996，17(4)：58-67.

[2] 余志成，施文华.深基坑护坡桩技术的几项新发展[J].建筑技术，1994，21(5)：272-279.

[3] 应宏伟，初振环,等.双排桩支护结构的计算方法研究及工程应用[J].岩土力学，2007，28(6)：1145-1150.

[4] 徐 凯，李俊才,等．双排桩支护结构在基坑支护中的应用研究[J].建筑科学，2013，1(4)：80-84.