惯质系数对车辆ISD悬架系统频率特性的影响研究

杨晓峰， 杜 毅， 刘雁玲， 胡健滨， 刘昌宁， 徐 旭

(1. 江苏大学 汽车与交通工程学院，江苏 镇江 212013；2. 江苏大学 理学院，江苏 镇江 212013)

惯容器是一种新型质量元件，作用于它两端点的力正比于两个端点相对加速度[1]，在各种机械隔振系统中使用惯容器能提升性能的事实已经得到了广泛证实[2-6]。通过将惯容器引入车辆悬架系统，对车辆悬架理论的研究产生了积极而深远的影响。研究表明[7-14]，对比传统悬架，应用惯容器的车辆悬架隔振性能得到明显提升。

在振动系统中，弹簧可以储存能量，提供静支撑，并且决定系统固有频率。阻尼器可以耗散能量，限制共振点的振幅。惯容器作为一种机械元件，也可以储存能量。根据元件的串并联关系，按照排列组合的方式，弹簧、阻尼和惯容器可以组成多种ISD(Inerter Spring Damper)悬架结构。在文献[15]中，仅仅以惯容器和弹簧并联的单自由度、二自由度和多自由度简单隔振系统为对象，研究了惯质系数变化对系统主频的影响，同时分析了系统主频对不同位置惯容器惯质系数的敏感程度。然而，对于惯质系数对各类ISD悬架系统偏频和主频特性的作用规律，还没有做过深入研究。

本文结合被动机械元件工作特点和元件排列组合方式，列出了10种可行的ISD悬架。在无阻尼自由振动情况下，根据无阻尼阻抗，将ISD悬架分成4类悬架，对其中3类含有惯容器的悬架进行深入研究分析。建立悬架动力学模型，推导并分析悬架的偏频和主频,研究惯质系数变化对这3类悬架系统偏频和主频特性的影响及其作用规律。

1 理论分析

1.1 机械阻抗理论

20世纪30年代初，通过机电比拟的方法提出来了机械阻抗方法的概念。机械阻抗被定义为各种激振频域下响应量和激振量的比值。数学上，阻抗与导纳互为倒数关系。惯容器的动力学表达式

(1)

式中：f为施加于元件两端点上等大反向的力；v1，v2为惯容器两端点的速度；b为惯质系数。

根据机械阻抗的定义，弹簧、阻尼和惯容器元件的机械阻抗表达式，如表1所示[16]。

表1 元件机械阻抗表达式

表1中：s为拉氏变换复变量；k为弹簧刚度；c为阻尼系数。

由n个阻抗为Yi的元件并联而成的系统等效阻抗Yp和由n个阻抗为Yi的元件串联而成的系统等效阻抗Ys表达式如下所示

(2)

(3)

1.2 ISD悬架及其阻抗

由于惯容器和阻尼是机械元件，必须处于有效的位置和行程范围内，否则元件会过载。因此车辆悬架内部的惯容器和阻尼必须要有弹簧的支撑，才能保证各元件的正常的工作，发挥各自的效果[17]。根据上述原理，并结合排列组合方式，图1左侧给出了10种可行的ISD悬架。

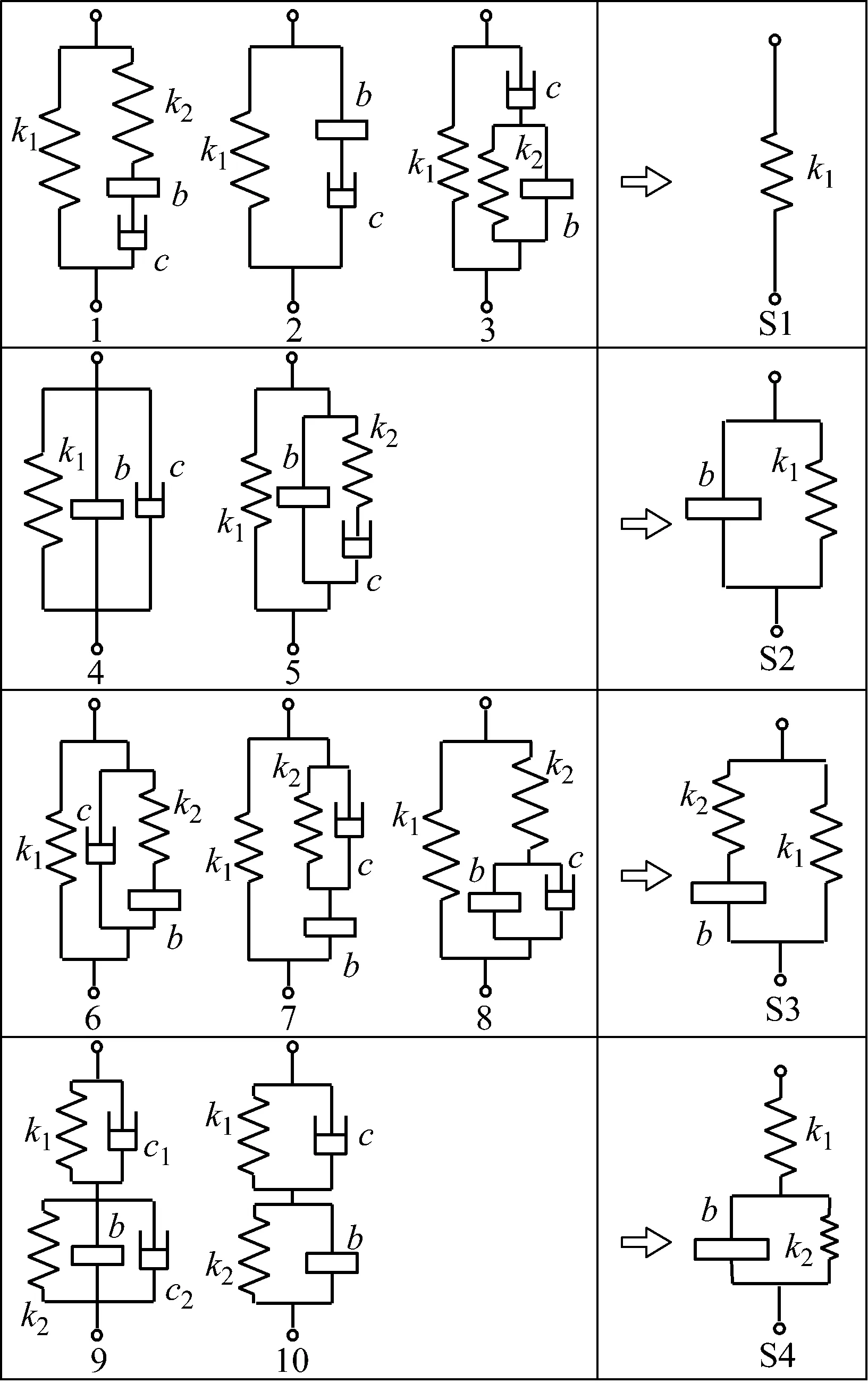
图1 10种ISD悬架及其无阻尼退化结构

根据机械阻抗以及串、并联系统的阻抗特性，可得图1中10种悬架的速度型机械阻抗，其中结构1、2、……、10对应的阻抗传递函数分别为Y1(s)、Y2(s)、……、Y10(s)

(4)

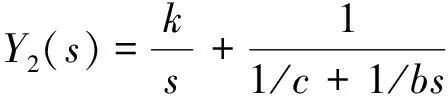
(5)

(6)

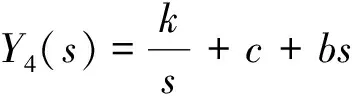
(7)

(8)

(9)

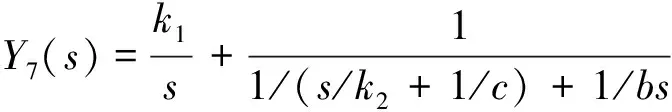
(10)

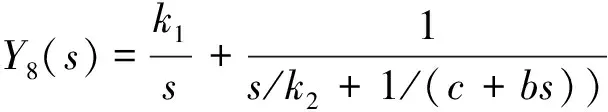
(11)

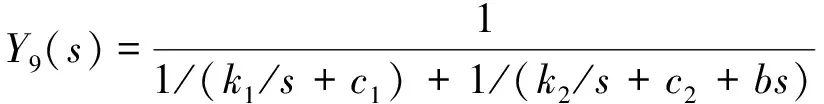
(12)

(13)

无阻尼自由振动时，悬架中阻尼为零，各个悬架的阻抗退化。将无阻尼阻抗相同的悬架归为一类，如表2所示。

表2 悬架分类

从无阻尼阻抗的表达式结构可以推出这类悬架的结构，图1种的10种ISD悬架结构退化成左侧的4种类型。由于退化的S1型悬架结构就是传统被动悬架的无阻尼结构，已经得到了充分研究，因此下文只对S2、S3、S4型悬架进行分析研究。

2 偏频与主频的推导

2.1 悬架系统动力学模型

应用复频域悬架阻抗法建立1/4模型，如图2所示。

从图2可知，1/4车辆悬架模型拉普拉斯变换下的动力学方程为

(14)

式中：mu为簧下质量；ms为簧上质量；zr为路面随机输入；zs，zu分别为簧上、簧下质量垂直位移；Zr，Zs，Zu分别为zr，zs，zu的拉氏变换形式；kt为轮胎刚度；Y(s)为复频域悬架阻抗。

2.2 推导过程

无阻尼自由(Zr=0)振动时，对于S2型悬架，计算方法如下。

2.2.1 车身偏频推导

将S2型悬架的阻抗表达式代入表达式(14)中，同时令mu不动(Zu=0)，即

(15)

显然，对于S2型悬架，车身偏频ω0是关于惯质系数b的单调减函数。

2.2.2 车轮偏频推导

将S2型悬架的阻抗表达式代入表达式(14)中，同时令ms不动(Zs=0)，即

(16)

显然，对于S2型悬架，车轮偏频ωt也是关于惯质系数b的单调减函数。

2.2.3 主频计算

设两个质量以相同的圆频率ω和相位角φ作简谐振动，振幅为zs0和zu0，则其解为zs=zs0ej(ωt+φ),zu=zu0ej(ωt+φ)，将zs和zu代入式(4)，化简计算得

(17)

此方程组要有非零解的条件是zs0和zu0的系数行列式为零，即

Δ(ω)=(msmu+msb+mub)ω4-

(muk+mskt+bkt+msk)ω2+kkt=0

(18)

式中：p=msmu+msb+mub+b2，q=muk+mskt+bkt+msk

ω1、ω2根式的分母中惯质系数b的最大次数为二次，而分子惯质系数b的最大次数为一次，因此对于S2型悬架，主频ω1、ω2也都是关于惯质系数b的减函数。

对于S3、S4这两类悬架的偏频和主频，用相同的计算方法分别进行推导，具体内容从略。将各类悬架计算所得的悬架偏频和主频数目整理，如表3所示。由表3各类悬架偏频和主频的数目得出，不同类型的悬架会造成偏频与主频数目的差异。

3 仿真分析

3.1 惯质系数对偏频和主频数值的影响

为研究S2、S3和S4型悬架中惯质系数对偏频和主频的影响，比较分析总结规律，利用车身1/4悬架模型，在MATLAB环境下进行数值仿真。同时在仿真图像3、4、5中加入了传统被动悬架的偏频和主频作为参考进行比较。传统被动悬架的弹簧刚度与表中悬架主弹簧刚度数值一致，簧载质量、非簧载质量和轮胎刚度与表4中的参数保持一致。

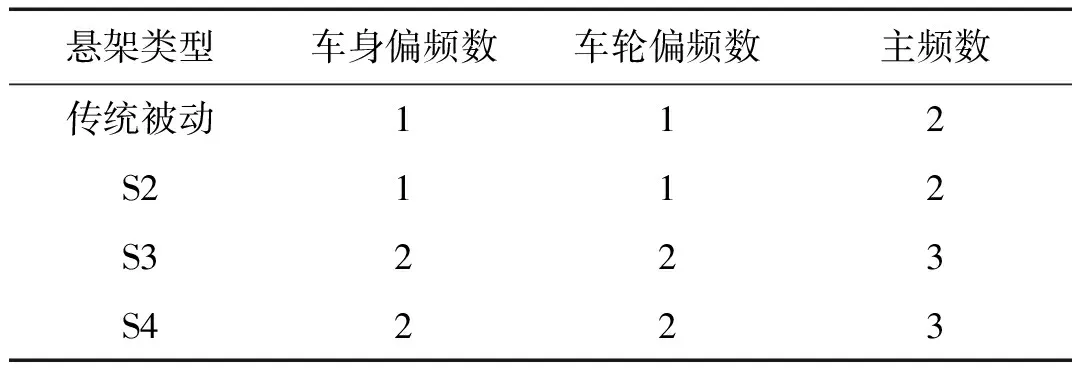
表3 悬架偏频主频数目

表4 系统参数

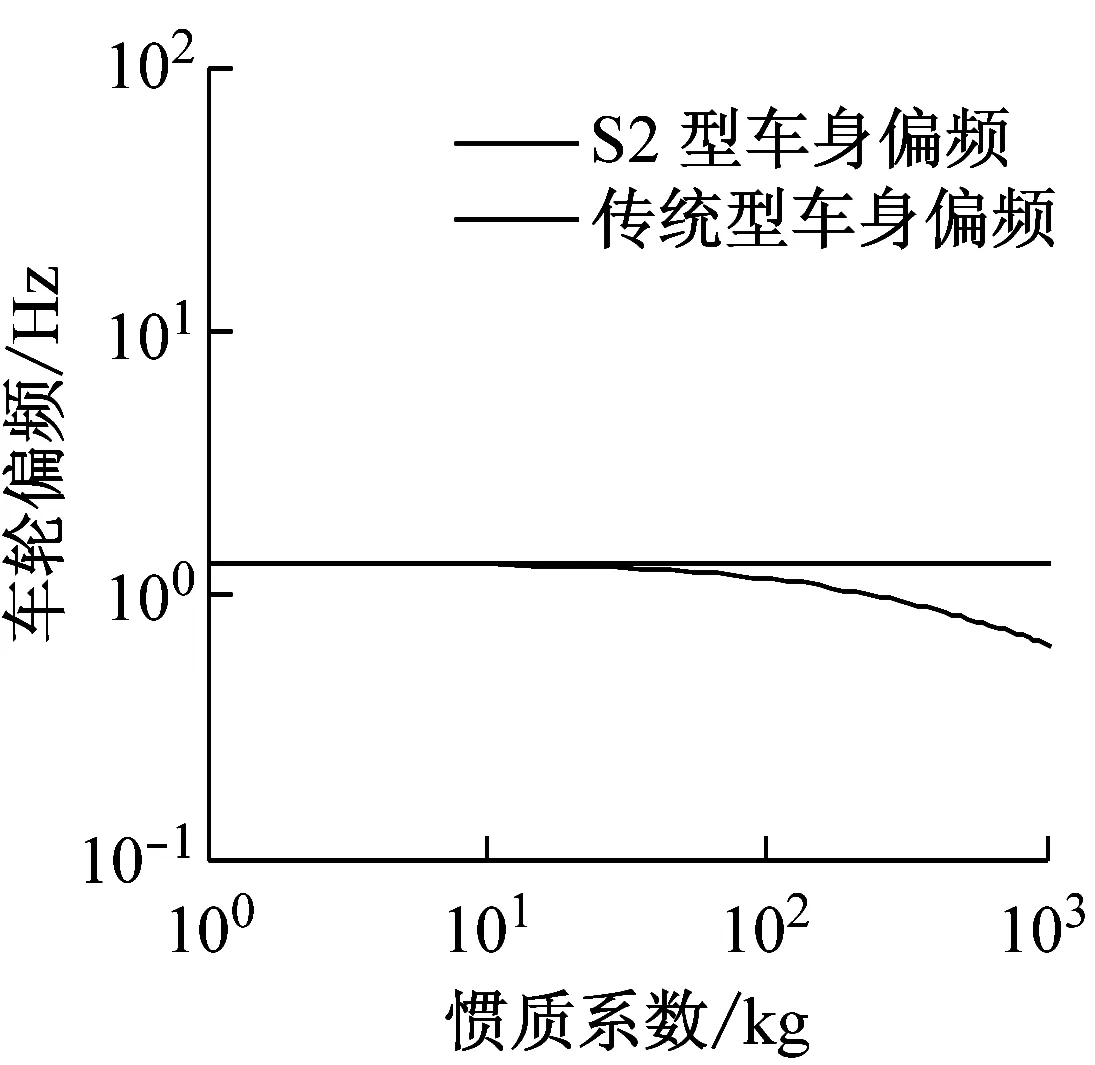
由图3可知，在惯质系数非零的情况下，S2型悬架的偏频和主频都始终小于传统型悬架对应的偏频和主频。因此，S2型悬架在降低固有频率方面较为显著。同时，S2型悬架的偏频和主频始终随着惯质系数的增加不断下降。

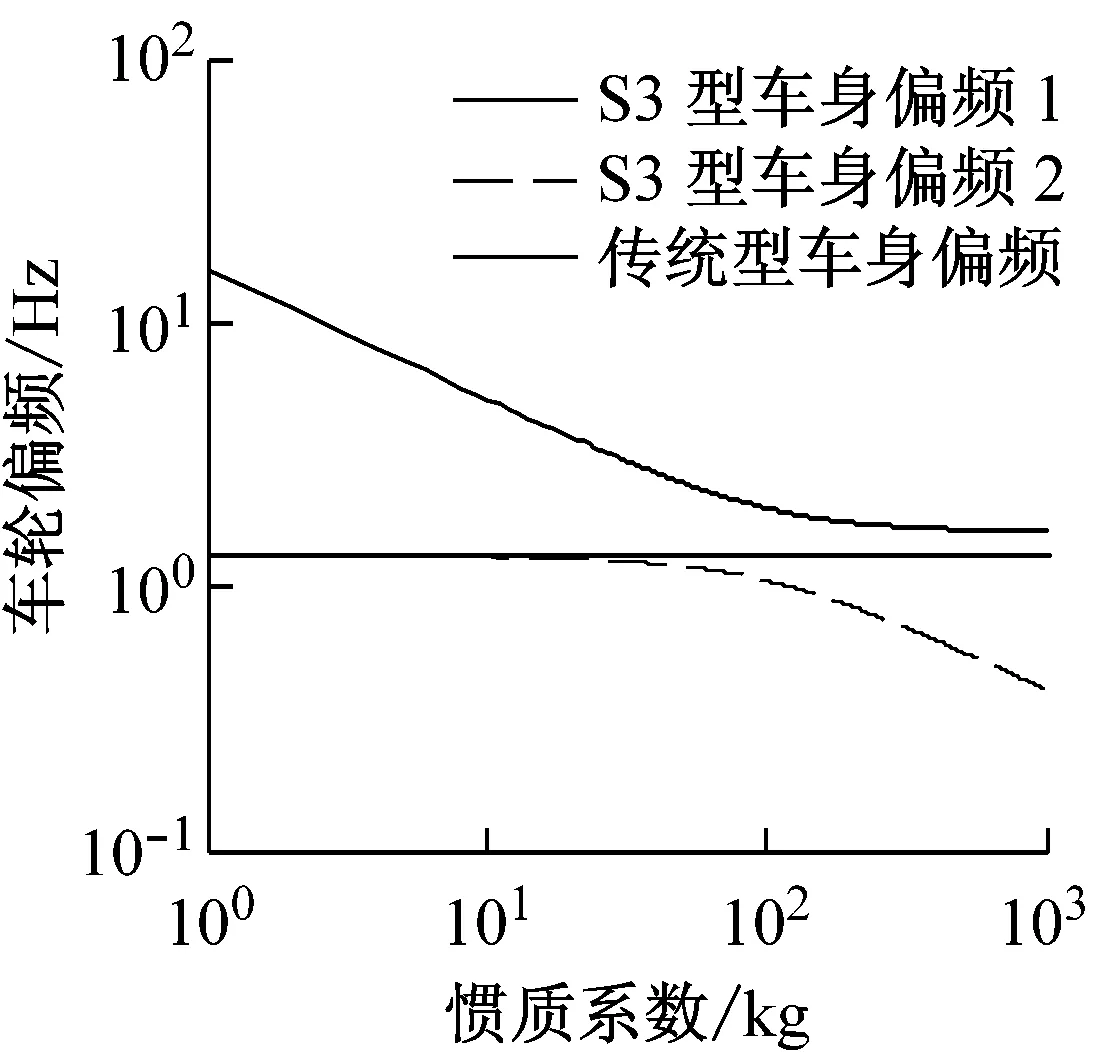
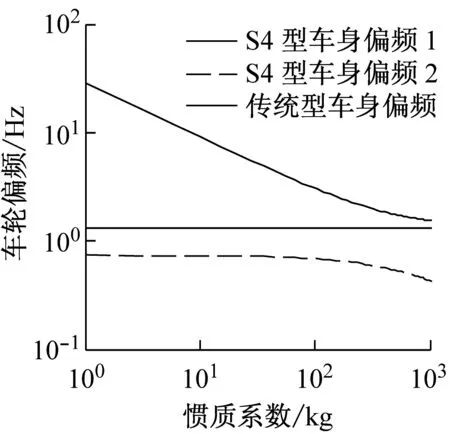
由图4和图5可知，S3和S4型图像特性类似。车身和车轮偏频分别位于传统型悬架车身和车轮偏频的两侧，主频分别位于传统型悬架两个主频的三侧。随惯质系数增加，车身偏频、车轮偏频和主频也都不同程度地在下降。同时，最大的偏频和主频在惯质系数达到一定数值时，就趋近于传统被动悬架的偏频和数值最大的主频。

总结图3、图4和图5中的图像特性，惯质系数确实能够有效降低S2、S3和S4型悬架的偏频和主频。

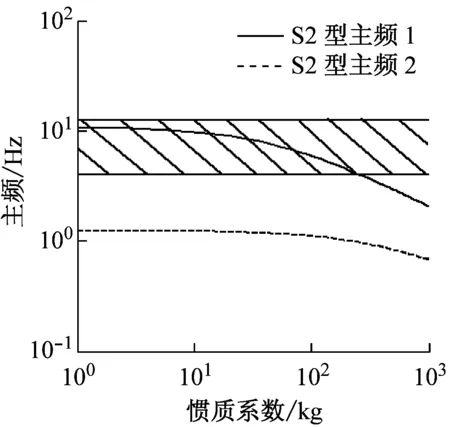
进一步研究主频，图6中阴影区域为4.0～12.5 Hz，为垂直方向人体最敏感的频率范围。随着惯质系数增加，S2型惯质系数超过300 kg，S3型惯质系数超过20 kg，S4型惯质系数超过50 kg后，使得悬架主频脱离人体敏感范围。也就说明了ISD悬架能够通过增加惯质系数，降低悬架自身主频，来使得悬架自身主频小于垂直振动敏感频率，从而改善汽车乘坐的舒适性。

3.2 惯质系数对偏频和主频的影响程度分析

保持表4种参数不变，通过观察在不同惯质系数条件下，增加1 kg惯质系数引起的S2、S3和S4类悬架偏频和主频的降幅。从而反映出在不同惯质系数条件下，惯质系数对偏频和主频的影响程度。

由图7可知，对于S2型悬架，在1～10 kg范围内，增加单位惯质系数引起的偏频和主频的降幅略有上升。而当惯质系数<10 kg后，偏频和主频的降幅随着惯质系数增加而下降。即随着惯质系数增加，惯质系数对偏频和主频的影响程度不断下降。

由图8和图9可知，S3和S4型悬架的特性类似，随着惯质系数增加，降幅基本呈现下降趋势。同时也能发现，在车身偏频和车轮偏频图像中，当惯质系数位于黑线左侧时，最大的偏频(车身偏频1和车轮偏频1)降幅最大。而当惯质系数位于黑线右侧时，最小的偏频(车身偏频2和车轮偏频2)降幅最大，同理主频图像也有类似特性。由此得出，在不同的惯质系数范围内，偏频和主频的降幅不同，即惯质系数对不同的偏频和主频的影响程度不同。

总结图7、图8和图9，虽然惯质系数能够有效降低S2、S3和S4型悬架偏频与主频，但随着惯质系数的增加，惯质系数对偏频与主频的影响程度不断下降。而且对于S3和S4类悬架，不同惯质系数数值区间内，惯质系数对不同的偏频和主频影响程度也不同。

4 结 论

(1)运用机械阻抗法，建立悬架动力学模型，推导并分析阻抗，分类研究ISD悬架的偏频和主频是一种有效的方法。

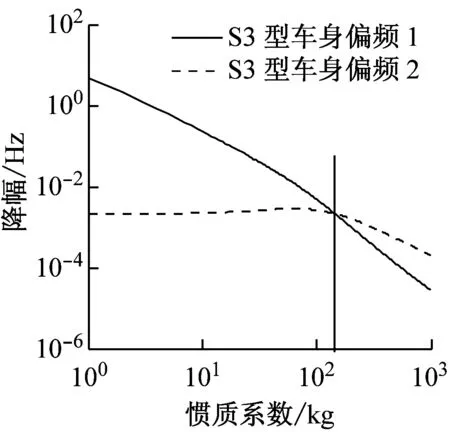
图8 S3型固有频率的降幅

Fig.8 The decreasing amplitude of natural frequencies of suspension S3

(2)由于惯容器质量阻抗的引入和新型机械网络拓扑特性的影响，使得不同类型ISD悬架系统偏频和主频数目有差异。

(3)增加惯质系数能有效降低S2、S3和S4型悬架偏频与主频，使得主频脱离垂直方向人体最敏感的频率范围。同时惯质系数对偏频与主频的影响程度随着惯质系数的增加而减小。

[1] SMITH M C. Synthesis of mechanical networks: the inerter[J]. IEEE Transactions on Automatic Control, 2003, 47(10):1657-1662.

[2] CHEN M Z Q, PAPAGEORGIOU C, SCHEIBE F, et al. The missing mechanical circuit element[J]. IEEE Circuits and Systems Magazine, 2009, 9(1):10-26.

[3] JIANG J Z, MATAMOROS-SANCHEZ A Z. Passive suspensions incorporating inerters for railway vehicles[J]. Vehicle System Dynamics, 2012, 50(1):263-276.

[4] LIMEBEER D J N, SHARP R S. Bicycles, motorcycles, and models[J]. IEEE Control Systems, 2006, 26(5):34-61.

[5] WANG F C, HONG M F, CHEN C W. Building suspensions with inerters[J]. ARCHIVE Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 1989-1996, 2010, 224(8):1605-1616.

[6] HANAZAWA Y, SUDA H, YAMAKITA M. Analysis and experiment of flat-footed passive dynamic walker with ankle inerter[C]// IEEE International Conference on Robotics and Biomimetics. IEEE, 2011:86-91.

[7] SMITH M C, WANG F C．Performance benefits in passive vehicle suspensions employing inerters[J]. Vehicle System Dynamics, 2004, 42(4): 235-257.

[8] 葛正, 王维锐. 车辆主动惯容式动力吸振悬架系统研究[J]. 振动与冲击, 2017，36(1):167-174.

GE Zheng, WANG Weirui. Vehicle active ISD-DVA suspension system[J]. Journal of Vibration and Shock, 2017，36(1):167-174.

[9] SHEN Y, CHEN L, YANG X, et al. Improved design of dynamic vibration absorber by using the inerter and its application in vehicle suspension[J]. Journal of Sound & Vibration, 2016, 361:148-158.

[10] WANG R, YE Q, SUN Z, et al. A study of the hydraulically interconnected inerter-spring-damper suspension system[J]. Mechanics Based Design of Structures and Machines, 2016:1-15.

[11] 杜甫, 毛明, 陈轶杰,等. 基于动力学模型与参数优化的ISD悬架结构设计及性能分析[J]. 振动与冲击, 2014, 33(6):59-65.

DU Fu, MAO Ming, CHEN Yitie, et al. Structure design and performance analysis of inerter-spring-damper suspension structure based on dynamic model and parameter optimization[J]. Journal of Vibration and Shock, 2014, 33(6):59-65.

[12] 陈龙, 张孝良, 江浩斌, 等. 基于机电系统相似性理论的蓄能悬架系统[J]. 中国机械工程, 2009, 20(10):1248-1251.

CHEN Long, ZHANG Xiaoliang, JIANG Haobin, et al. Vehicle suspension system employing inerter based on electrical-mechanical analogy theory[J]. China Mechanical Engineering, 2009, 20(10):1248-1251.

[13] 陈龙, 张孝良, 聂佳梅, 等. 基于半车模型的两级串联型ISD悬架性能分析[J]. 机械工程学报, 2012, 48(6):102-108．

CHEN Long, ZHANG Xiaoliang, NIE Jiamei, et al. Performance analysis of two-stage series-connected inerter-spring-damper suspension based on half-car model[J]. Journal of Mechanical Engineering, 2012, 48(6):102-108.

[14] ZHANG X J, AHMADIAN M, GUO K H. On the benefits of semi-active suspensions with inerters[J]. Shock and Vibration, 2012, 19(3):257-272.

[15] CHEN M Z Q, HU Y, HUANG L, et al. Influence of inerter on natural frequencies of vibration systems[J]. Journal of Sound and Vibration, 2014, 333(7):1874-1887.

[16] 陈龙, 杨晓峰, 汪若尘, 等. 基于二元件ISD结构隔振机理的车辆被动悬架设计与性能研究[J]. 振动与冲击，2013, 32(6):90-95.

CHEN Long, YANG Xiaofeng, WANG Ruochen, et al. Design and performance study of vehicle passive suspension based on two-element inerter-spring-damper structure vibration isolation mechanism[J]. Journal of Vibration and Shock, 2013, 32(6): 90-95.

[17] 陈龙, 杨晓峰, 汪若尘, 等. 改进的ISD三元件车辆被动悬架性能的研究[J]. 汽车工程, 2014, 36(3):340-345.

CHEN Long, YANG Xiaofeng, WANG Ruochen, et al. A study on the performances of vehicle passive suspension with modified inerter-spring-damper three-element structure[J]. Automotive Engineering, 2014, 36(3):340-345.