表面粗糙度对导线风荷载及涡激振动的影响

晏致涛, 王灵芝, 刘 军, 游 溢,3,孙 毅

(1.重庆科技学院 建筑工程学院，重庆 401331;2.重庆大学 土木工程学院，重庆 400045;3.国网新疆电力公司电力科学研究院，乌鲁木齐 830011)

作为一种大跨柔性结构，传统输电导线形式大多为由多股铝绞线缠绕在一起的圆形钢芯铝绞线。近年来随着特高压输电工程的迅速发展，对输电导线的气动性能的要求也逐渐增加[1]。输电导线的截面形状对导线的气动力特性有重要影响，导线受到的风压占整个输电线路风压的50%～70%。为了改善导线的气动性能，许多具有新型截面型式的大直径导线结构被广泛运用于工程实际[2]。而以往对于导线的气动特性的研究，大多数都将导线截面简化为光滑的圆形截面，忽略了导线表面粗糙度的影响。真实输电导线及其模型,如图1所示。

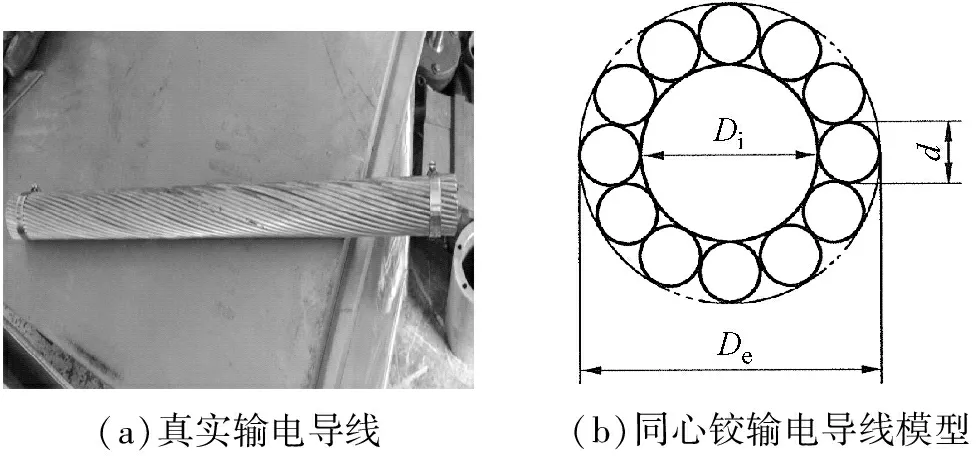
(a)真实输电导线(b)同心铰输电导线模型

图1 真实输电导线及其模型

Fig.1 Model of the real transmission conductor with rough cross-section

随着计算机技术的发展，采用数值计算方法研究复杂流动问题日益成熟[3-5]。苏铭德等[6]采用Smagorinsky涡黏性模型和有限体积法，对雷诺数Re为100～20 000的光滑圆形柱体截面进行了数值计算。陈文礼等[7]采用基于湍流模型方法的CFX中剪切应力输运湍流模型，研究了光滑圆截面在不同来流风速条件下的涡致振动特性。何长江等[8]利用动态网格层铺模型和滑移网格模型，通过用户自定义接口编程，建立了二维圆柱体横向涡激振动的数值计算模型，并计算了雷诺数处于6 000～20 000变化范围内具有不同质量-阻尼参数条件下的柱体振动。周国成等[9]基于SSTk-ω湍流模型，运用CFX动网格层铺技术，研究了Re约为3 900下圆形柱体的二维涡激振动，得到了圆柱体涡激振动的自激自限的性质。董国朝[10]分别采用SST湍流模型与LES模型对不同雷诺数下的三维圆柱体进行了非定常绕流的数值模拟计算。孙启刚等[11]采用流体力学计算软件，对新型低阻LP810导线进行雷诺数为76 000时气动力特性以及流场的数值模拟。

上述分析均基于光滑圆柱绕流，并没有考虑钢芯铝绞线的表面粗糙特性对导线气动力以及涡激振动的影响。本文采用流体力学计算软件FLUENT，对型号为JL/GIA 900/75的真实粗糙截面导线及其常规简化的光滑截面导线进行CFD(Computational Fluid Dynamics)数值建模，并对导线在高雷诺数下的气动力特性以及涡激振动进行模拟分析。针对两种不同截面型式的导线，分析导线表面粗糙度对导线气动力和振动特性的影响。

1 流固耦合分析方法

黏性流体力学中，流体的运动规律可用N-S方程来描述，其在惯性直角坐标系下的连续性方程以及动量方程可表示为

(1)

(2)

式中:ρ为流体密度;t为流动时间;i,j=1,2,3;μ为流体的动力黏性系数；Fi是流体微元体上i方向的压力。

柱体绕流振动计算模型可简化为一个质量-刚度-阻尼体系。定义M,K和C分别为体系的质量、弹簧刚度和阻尼，则其三自由度模型的振动方程可表示为

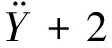
(3)

式中:ξ、ω0分别为弹簧阻尼系统的阻尼比和圆频率；M为体系展向长度为单位长度下截面质量;Iz为体系的转动惯量；X,Y,Z分别为截面沿流向、横向、扭转向的位移(角位移)，其一阶导数为相应的速度(角速度)，二阶导数为对应加速度(角加速度)；Fd(t)、Fl(t)、Fm(t)分别为单位长度截面所受到的阻力、升力和扭转力。

2 计算模型及设定

2.1 计算域及网格

选择二维矩形流体域作为计算区域，定义初始坐标原点与导线形心重合，水平方向为流向，竖直方向为横向，流体计算域上游来流区域长度25D(D为导线迎风面参考长度)，下游尾流区域取为65D以保证湍流的充分发展，上下边界取30D以满足阻塞率和动网格要求；在FLUENT计算中，二维模型默认的展向长度为1 m，本文雷诺数处于高雷诺数的亚临界区范围内，湍流模型采用SSTk-ω湍流模型。边界条件设置如下：流体至左向右流动，左侧进口边界设定为速度入口边界，来流速度均匀；右侧为流动出口边界，压力出口，参考压力设置为0；上下边界定义为对称边界；圆柱体表面定义为无滑移壁面。

流场计算域以及计算网格是CFD数值计算的载体，网格质量的高低直接关系到计算过程能否顺利进行以及计算结果的精确性。本文采用ICEM对计算域进行结构化网格划分，考虑到导线附近流场的变化较剧烈，对近壁面处的网格进行加密处理，并控制壁面网格高度以减小网格对数值计算的影响。流体计算域的整体网格划分,如图2所示。两种截面导线近壁面处网格划分,如图3所示。

图2 流体计算域网格

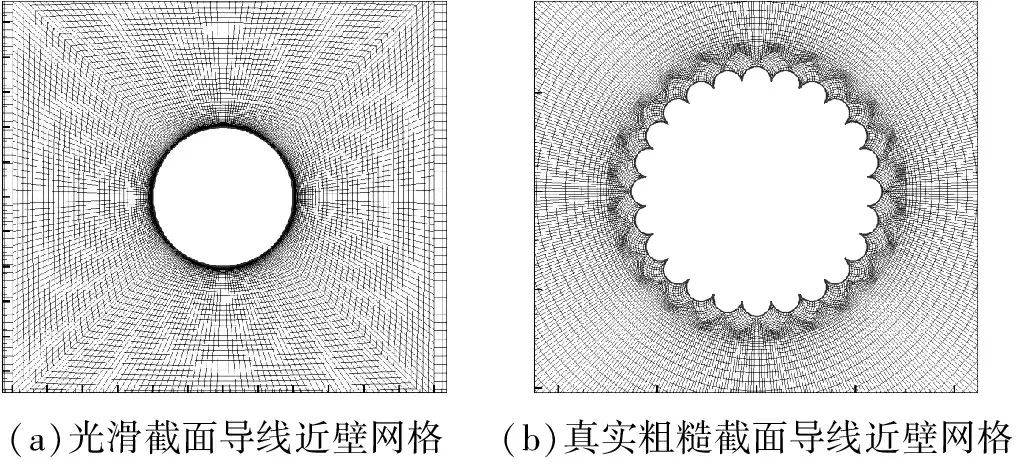
(a)光滑截面导线近壁网格(b)真实粗糙截面导线近壁网格

图3 导线近壁面网格示意图

Fig.3 Local grid refinement of smooth section conductors and real rough section conductors

2.2 计算参数和工况

本文数值模拟分析中，结构参数分别为，空气密度ρ=1.225 kg/m3，导线直径D=40.6 mm，质量比m*=248(m*=m/(1/4πρD2L))，导线自振频率fn=4.0 Hz，折减风速Ur=4.33～10.149(Ur=U∞/fnD)。高雷诺数下时间步长取值对数值计算精度有一定影响，本文采用定义无量纲时间步长t′(t′=tU/D)进行衡量，针对不同的来流风速，采取不同的时间步长进行计算并与以往研究结果进行比较从而确定其对应的计算步长，本文最终采用的t′取值约为0.12。

其余无量纲参数定义如下：雷诺数Re=ρUD/μ=UD/υ；斯托劳哈尔数St=fsD/U；无量纲横向位移Y=y/D。其中:fs为涡脱落频率;fy1,fy2为导线振动的前两阶主频;y为导线的横向振动位移。

FLUENT只是纯粹的CFD计算软件，并不能直接进行固体结构响应的求解，若要实现流固耦合计算，需要编写相应的程序求解结构的响应。根据上一节理论，通过编写用户自定义程序，采用Newmark-β法求解结构动力响应，利用动网格和滑移网格技术实现计算域内网格动态更新，最终实现输电线的流固耦合求解。

3 导线风荷载及涡振分析

3.1 精确度验证

为了验证本文所采用的数值模拟方法的精确度，首先对不同雷诺数下光滑圆形截面导线的固定绕流进行数值分析，将得到的气动阻力系数均值结果与以往试验数据进行比较，结果如图4所示。Cd为导线的阻力系数。图4(a)结果表明：在低雷诺数下，截面的阻力系数均值随雷诺数增加迅速下降；采用本文的计算思路所得到的CFD模拟结果与之前学者的实验数据吻合良好；由图4(b)可知，在高雷诺数下，光滑截面导线阻力系数均值基本保持平稳，保持在约1.2，与Khalark的结果一致。由此可以说明采用本文的网格划分策略及数值计算能够满足精度要求。

(a)低雷诺数下Cd均值

(b)高雷诺数下Cd均值

Fig.4 The mean of the aerodynamic drag coefficient of smooth cross-section conductors with different Reynolds number

此外，图5给出了来流风速分别为7.7 m/s和21.7 m/s时，真实粗糙截面导线和光滑截面导线数值模拟结果以及原型导线的风洞试验结果。可见，两种风速下，真实的粗糙截面导线结果更接近风洞试验的实验值。图4和图5的对比结果表明，本文所采用的计算模型有良好的精确性和可靠性。

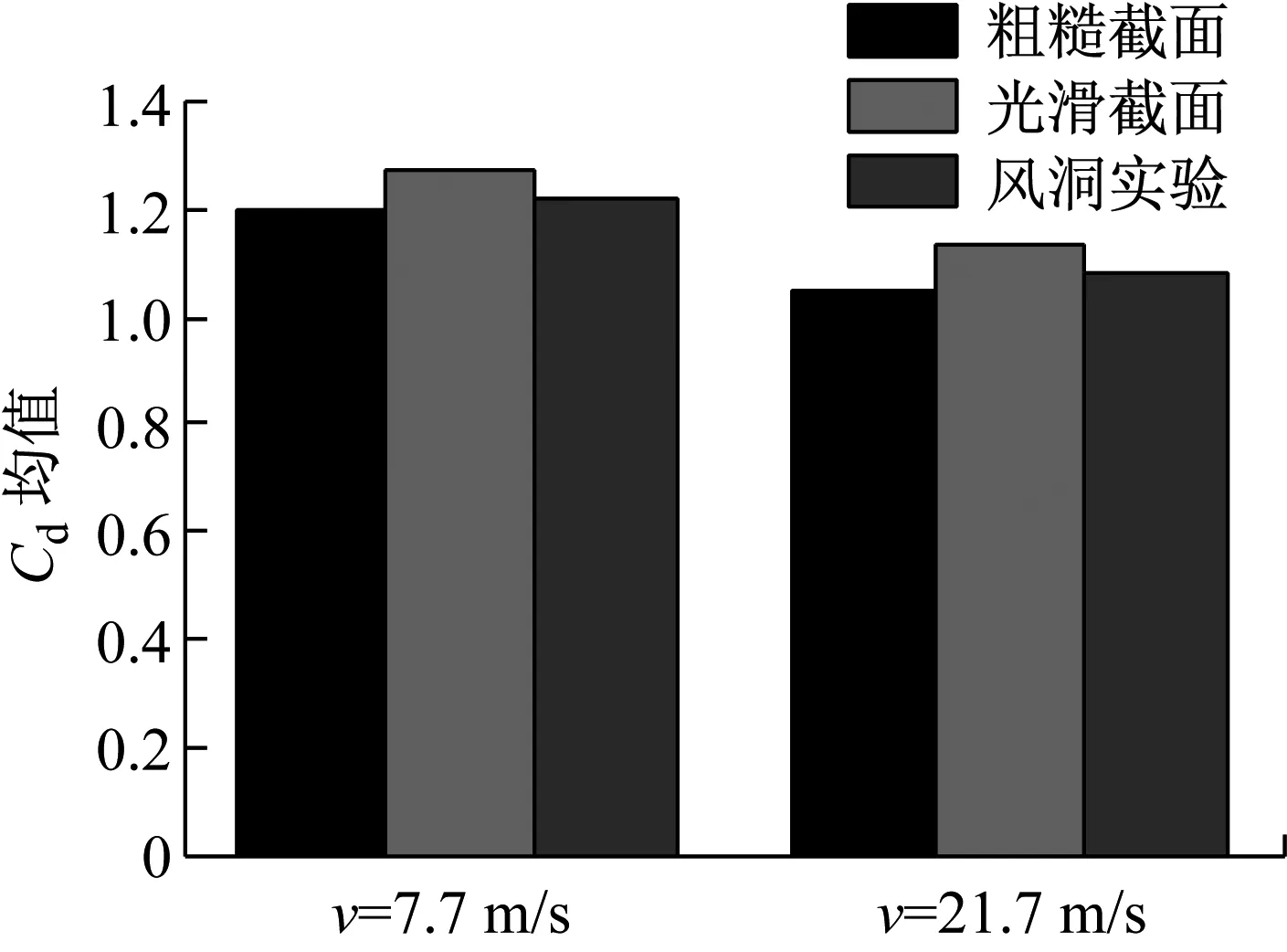
图5 两种风速下不同截面型式导线气动阻力系数均值

Fig.5 The mean of the aerodynamic drag coefficient of two kinds of cross-section conductors with different wind speed

3.2 导线气动力特性

对真实的粗糙截面以及常规光滑截面导线在不同风速下的气动特性进行数值分析，结果如图6所示。由图6(a)、图6(b)可知，导线固定状态下，光滑导线的阻力系数均值和均方根值随折减风速增加基本保持平稳，升力系数最大值和均方根值均略有小幅增加；真实粗糙截面导线的气动力系数特征值变化趋势基本一致，均是先增大再减小最后保持上升趋势。此外，在同一折减风速下，粗糙截面导线的气动力特征值均比光滑截面导线小，由此可以认为：导线表面的粗糙度可以降低流体对固定导线的作用力。

对导线的气动力进行频谱分析，由图6(c)可知，粗糙截面导线阻力系数主频约为升力系数主频的两倍，这与光滑截面导线的结果类似；在折减风速较低时，粗糙截面导线与光滑截面导线的频率值基本相等，而随着折减风速增加，真实粗糙截面导线的主频要略微小于光滑截面导线的频率值，表明导线的表面粗糙度略微增大了导线气动力的变化周期。

进一步分析表面粗糙度对固定导线漩涡脱落的影响。图6(d)给出了粗糙截面导线与光滑截面导线的斯托劳哈尔数随折减风速的变化规律。由图6(d)可知，固定状态下光滑导线的St值随折减风速增加基本维持在约为0.2；而粗糙截面导线的St数始终小于同条件下光滑截面导线的St数，即导线的表面粗糙度减小了导线表面漩涡的脱落频率。由此可以认为，导线的表面粗糙度减小了漩涡的脱落频率，增大了导线气动力的变化周期。

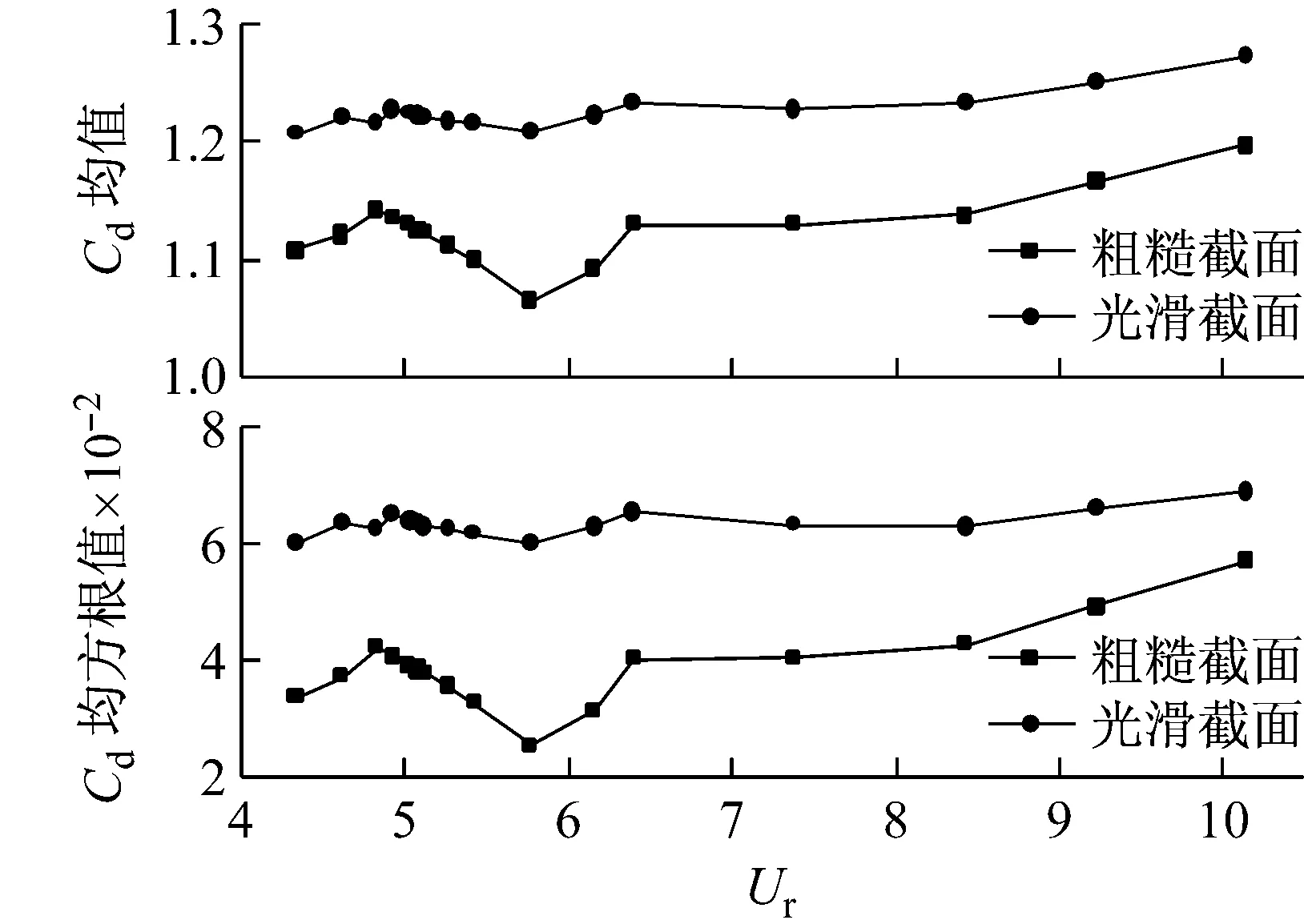
(a)阻力系数Cd

(b)升力系数Cl

(c)频率比

(d)St

3.3 导线横向涡振分析

以雷诺数处于亚临界区域为例，对真实粗糙截面导线以及光滑截面导线的横向振动进行流固耦合数值模拟分析，研究导线表面粗糙度对导线涡激振动响应的影响。

图7(a)、图7(b)分别给出了两种截面型式导线横向振动时气动力系数特征值随折减风速的变化规律。可知，随着折减风速增加，光滑截面导线的气动升阻力系数均出现先增大后减小最后保持平稳的变化规律；而真实粗糙截面导线的气动升阻力系数则是先增大再减小再略微增大趋向平稳的规律。这一结果说明导线的横向振动改变了其气动力的变化规律。此外，在折减风速较低和较高时，粗糙截面导线的阻力系数均值、均方根值以及升力系数最大值均小于光滑截面导线；而其升力系数均方根值则明显大于光滑截面导线；而且，考虑导线表面粗糙度后的气动力特征值变化更为剧烈，且剧烈变化区域所对应的折减风速范围有所增加，极值所对应的折减风速也有所增大。

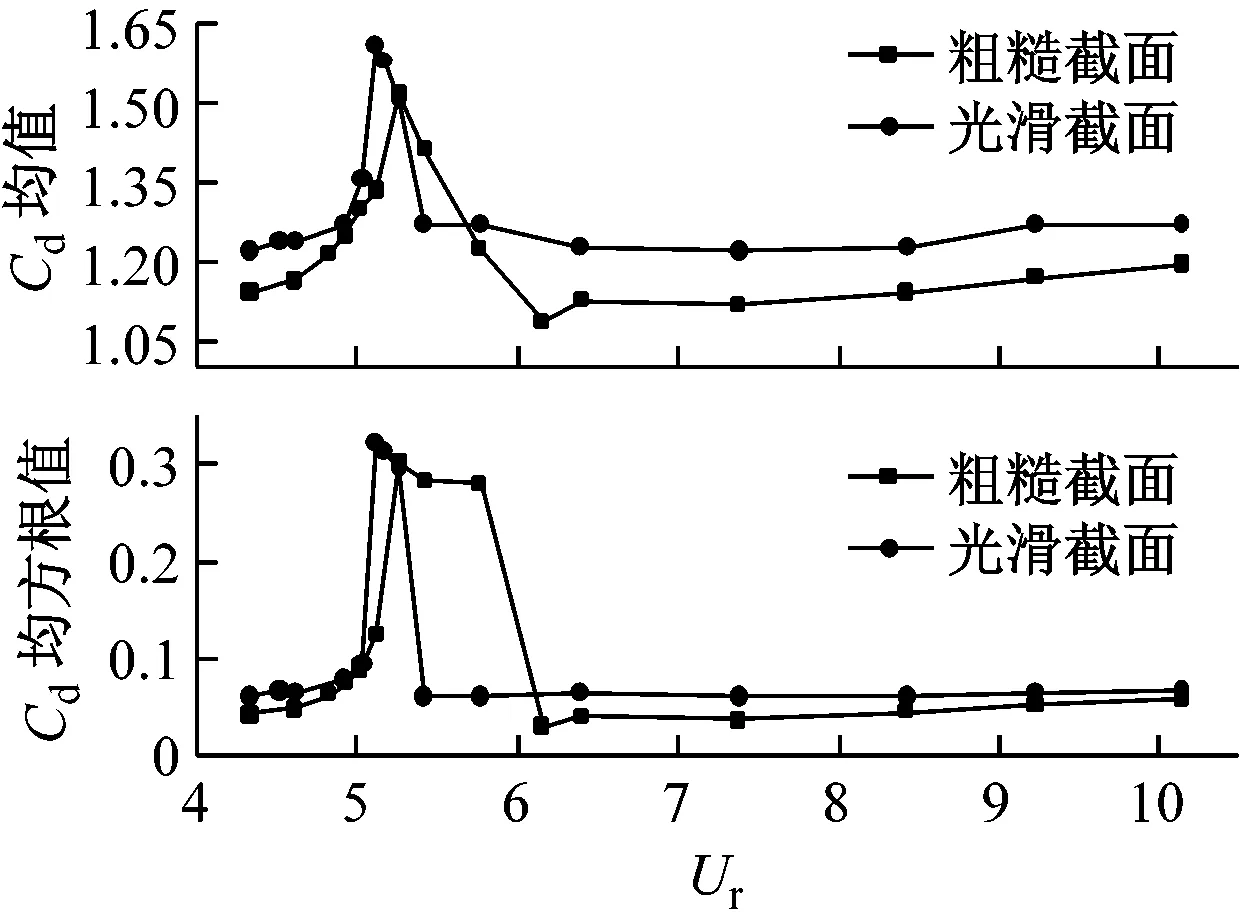
(a)Cd

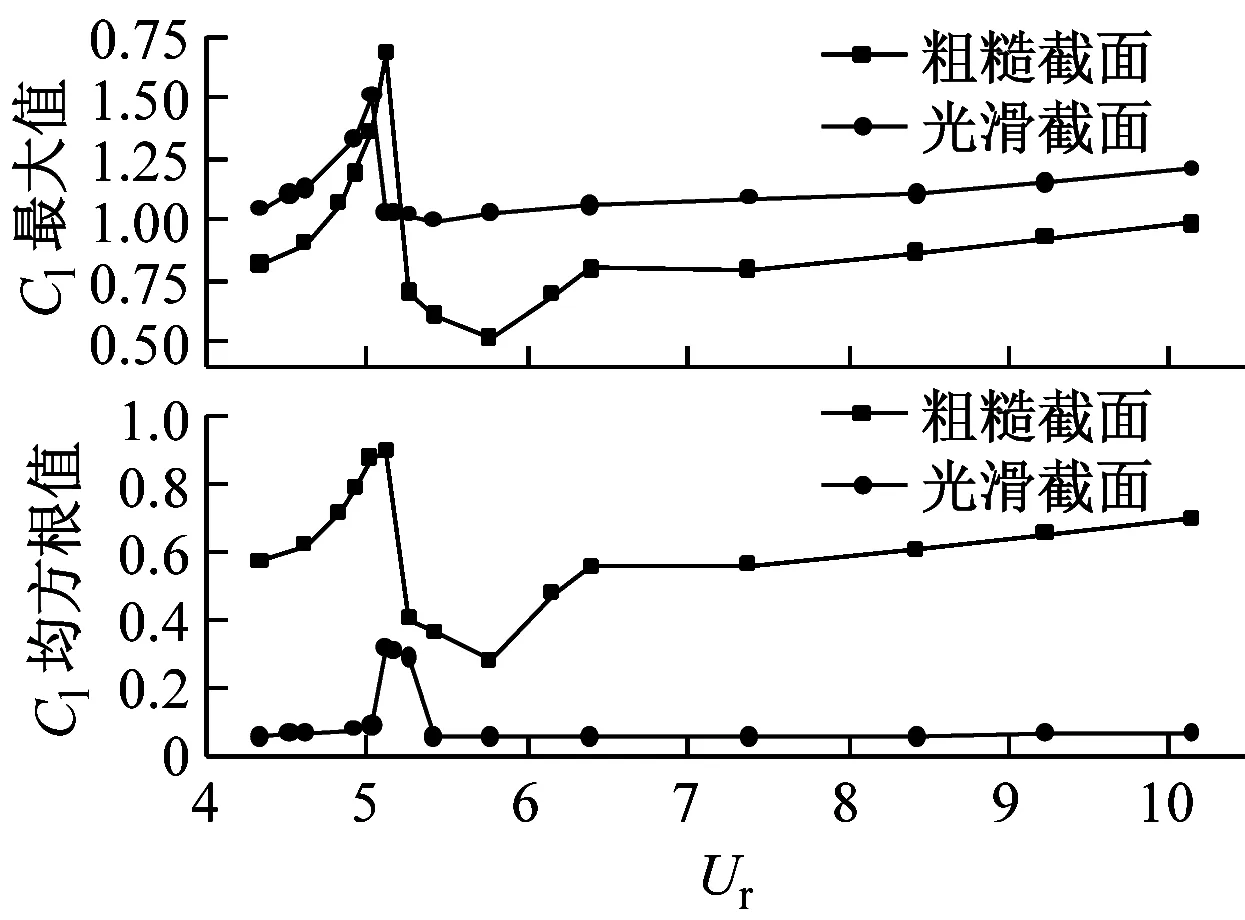
(b)Cl

(c)频率比

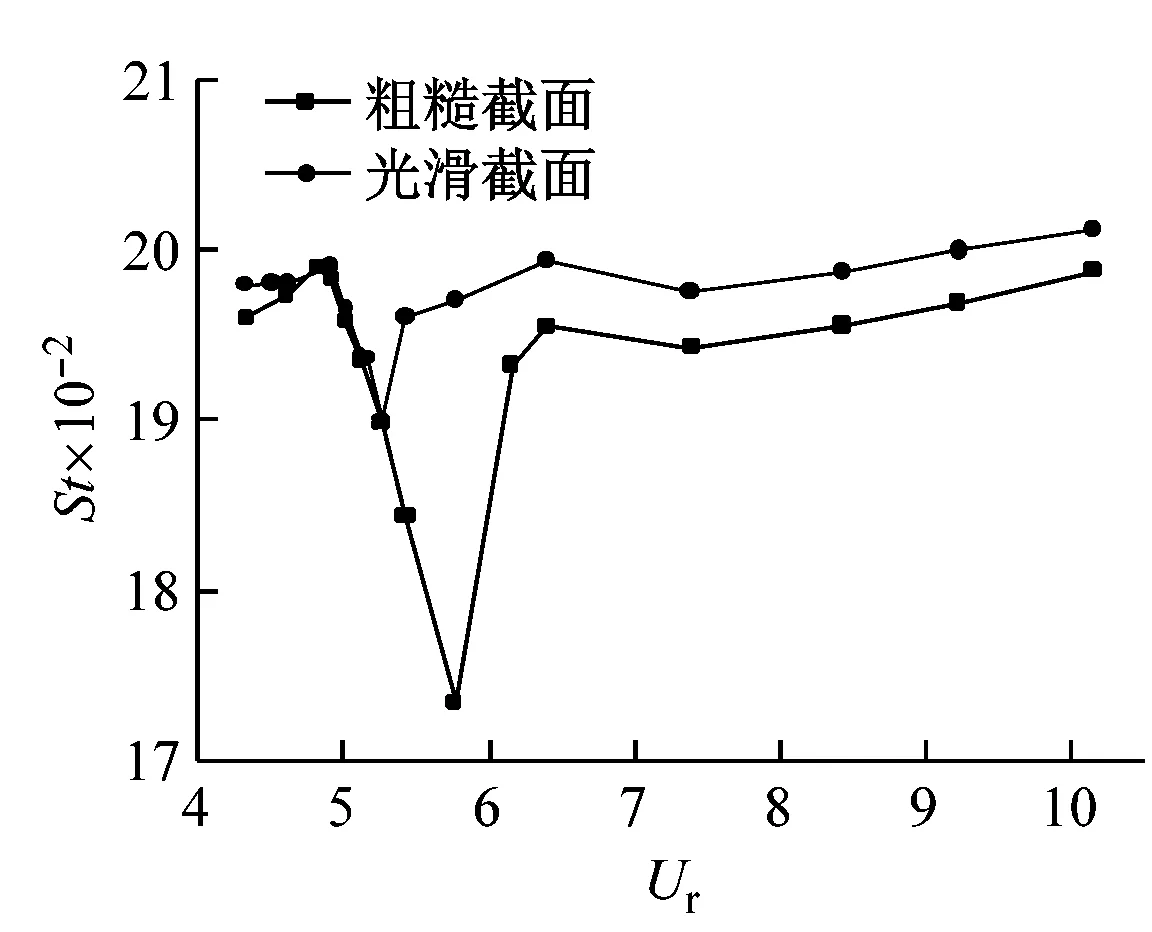
(d)St值

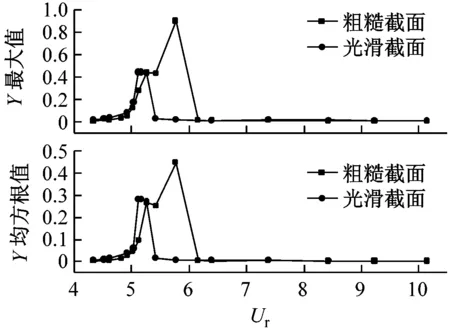
(e)无量纲振动位移幅值Y

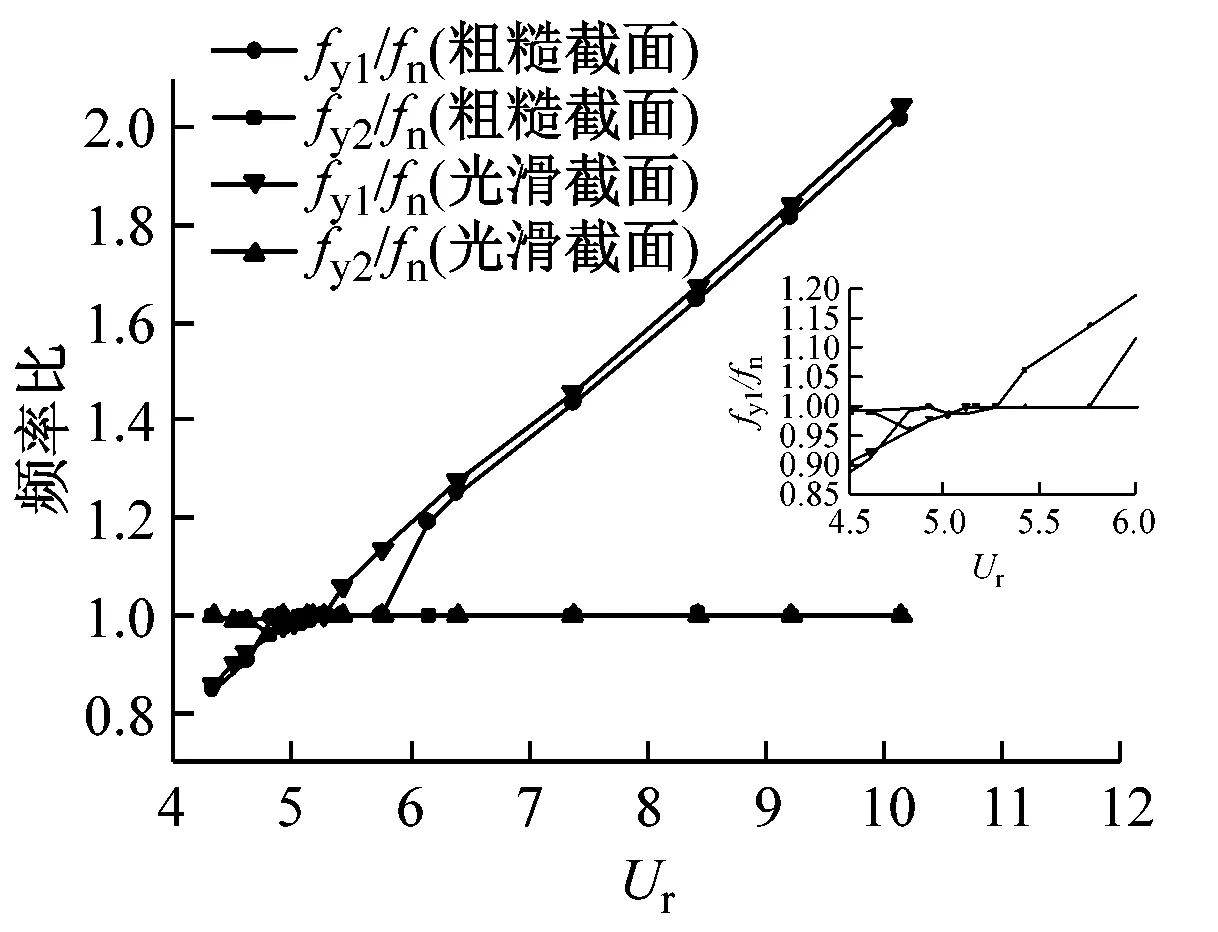
(f)横向振动频率比

Fig.7 Aerodynamic coefficient and transverse displacement of the real rough cross-section conductors with transverse vibration considered under different reduced wind speed

图7(c)、图7(d)为两种截面型式导线涡激振动时气动力系数主频以及St值随折减风速变化规律。结果表明，在折减风速较低以及较高范围内，两种截面型式导线的气动力主频大致相等，且均随折减风速增加而增加；而St值，两种截面结果在均随折减风速的增大而增大的情况下，粗糙截面的结果始终略小于光滑截面导线的结果。此外，当折减风速为5～6时，两种截面导线的气动力主频不再随折减风速增加而增加，St值也出现剧烈波动，此时“锁定”现象出现。且在“锁定”区，粗糙导线的气动特性比光滑导线变化更为剧烈。

图7(e)给出了两种导线横向振动位移响应(无量纲位移Y=y/D)最大值以及均方根值随折减风速的规律变化。结果说明，两种截面导线的位移响应最大值以及均方根值随折减风速增大均出现先增大后减小的变化趋势。与光滑导线相比较，真实粗糙截面导线的 “锁定”区域范围要广，峰值响应所对应的风速也大一些，且其最大振动幅值达0.9D，远大于光滑截面的振动幅值。

对导线的横向位移时程进行频谱分析，得到位移主频关系,如图7(f)所示。其中，fy1,fy2分别为导线横向振动一阶、二阶主频，fn为导线的自振频率。由图7(f)可知，在非“锁定”区，导线的横向振动出现两个主频：其中一个为结构的自振频率，另一个为漩涡的脱落频率，且真实截面的一阶主频要略小于光滑截面，锁定区长度大于光滑截面。由此说明，导线的表面粗糙度对导线的横向振动有影响。

导线涡激振动的主要原因是结构表面漩涡的交替脱落引起的不平衡气动力。对导线所在流场进行可视化分析，可以得到导线的涡脱规律。折减风速下真实导线截面和光滑截面在四个不同时刻的流场分布图,如图8所示。由图8可知，考虑导线表面粗糙度影响后，漩涡在每一根绞线上均有可能产生流动分离现象并形成细小的漩涡脱落，这一点不同于光滑柱体截面；而在远离柱体的下游，则汇合形成统一的涡街，这与光滑截面导线一致。

4 结 论

为研究导线表面粗糙度对导线振动响应的影响，利用ICEM对流体计算域进行结构化网格划分，采用动网格和滑移网格技术以及用户自定义接口编程, 将计算结构响应的Newmark-β代码嵌入FLUENT软件，分别对真实粗糙截面导线以及常规光滑截面导线进行数值模拟分析，得到以下结论。

(1)两种截面导线的固定绕流结果表明，与光滑截面导线相比，真实粗糙截面导线的气动力特征值要更小，说明结构表面的粗糙度降低了流体对结构的作用力，但增大了结构的气动力变化周期。

(2)两种截面型式导线的横向流固耦合振动响应结果表明，与光滑截面导线相比，真实粗糙截面导线的气动力和振动幅值出现峰值所对应的折减风速有所增加；导线的 “锁定”区域范围要广，变化更为剧烈，且其最大振动幅值远大于光滑截面导线的振动幅值；对导线的流场进行可视化分析，发现粗糙截面导线的漩涡分离点并不单一。

(a)真实粗糙截面导线

(b)光滑截面导线

[1] ZHOU C Y, SO R M C. Vortex induced vibrations of an elastic circular cylinder[J]. Journal of Fluids & Structures, 1999, 13(2):165-189.

[2] 党朋, 吴细毛, 刘斌. 新型同心绞导线风阻力系数风洞试验[J]. 电线电缆, 2014, 4(1):30-33.

DANG Peng, WU Ximao, LIU Bin. Wind tunnel test on drag coefficient of new type concentric lay stranded conductors[J]. Electric Wire & Cable, 2014, 4(1):30-33.

[3] KIM S, WILSON P A, CHEN Z M. Numerical simulation of force and wake mode of an oscillating cylinder[J]. Journal of Fluids & Structures, 2014, 44(7):216-225.

[4] KIKUCHI N, MATSUZAKI Y. Aerodynamic drag of new-design electric power wire in a heavy rainfall and wind[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(1/2):41-51.

[5] 李新民, 朱宽军, 刘彬. 典型覆冰导线空气动力学特性数值和试验模拟[J]. 高电压技术, 2014, 40(2): 427-433.

LI Xinmin, ZHU Kuanjun, LIU Bin. Numerical and experimental simulation of aerodynamic characteristics of typical iced conductor[J]. High Voltage Engineering, 2014, 40(2): 427-433.

[6] 苏铭德, 康钦军. 亚临界雷诺数下圆柱绕流的大涡模拟[J]. 力学学报, 1999, 31(1):100-105.

SU Mingde, KANG Qinjun. Large eddy simulation of the turbulent flow around a circular cylinder at sub-critical Reynolds numbers[J]. Acta Mechanica Sinica, 1999, 31(1):100-105.

[7] 陈文礼, 李惠. 基于RANS的圆柱风致涡激振动的CFD数值模拟[J]. 西安建筑科技大学学报(自然科学版), 2006, 38(4):509-513.

CHEN Wenli, LI Hui. CFD numerical simulation of vortex-induced vibration of a circular cylinder based on a RANS method[J]. J Xi’an Univ of Arch & Tech (Natural Science Edition), 2006, 38(4):509-513.

[8] 何长江, 段忠东. 二维圆柱涡激振动的数值模拟[J]. 海洋工程, 2008, 26(1):57-63.

HE Changjiang, DUAN Zhongdong. Numerical simulation of vortex-induced vibration on 2D circular cylinders[J]. The Ocean Engineering, 2008, 26(1):57-63.

[9] 周国成, 柳贡民. 圆柱涡激振动数值模拟研究[J]. 噪声与振动控制, 2010, 30(5):51-55.

ZHOU Guocheng, LIU Gongmin. Numerical simulation of vortex-induced vibration of a circular cylinder[J]. Noise and Vibration Control, 2010, 30(5):51-55.

[10] 董国朝. 钝体绕流及风致振动流固耦合的CFD研究[D]. 长沙: 湖南大学, 2012.

[11] 孙启刚, 谢强, 宋卓彦. 新型低阻导线气动特性数值模拟[J]. 国网技术学院学报, 2014, 17(6):12-18.

SUN Qigang, XIE Qiang, SONG Zhuoyan. Numerical simulation of aerodynamic characteristics of new low resistance wire[J]. Journal of State Grid Technology College, 2014, 17(6):12-18.

[12] TRITTON D J. Experiments on the flow around a circular cylinder at low Reynolds number[J]. J Fluid Mech, 1959,6:547-567.

[13] DENNIS S C R, CHANG G Z. Numerical solutions for steady flow past a circular cylinder at Reynolds numbers up to 100[J]. J Fluid Mech, 1970, 42(3):471-489.

[14] ZDRAVKOVICH M M. Flow around circular cylinders Vol.2: Applications[M]. Oxford: Oxford Science Publications, 2003.

[15] KHALAK A, WILLIAMSON C H K. Dynamics of a hydroelastic cylinder with very low mass and damping[J]. Journal of Fluids and Structures, 1996, 10(5):455-472.

[16] NORBERG C. Fluctuating lift on a circular cylinder: review and new measurements[J]. Journal of Fluids and Structures, 2003, 17(1): 57-96.