多级载荷累积损伤下结构的动态可靠性分析
孙剑萍 汤兆平 罗意平
1.华东交通大学交通运输与物流学院,南昌,3300132.中南大学交通运输工程学院,长沙,410075
0 引言
结构的可靠性往往与时间密切相关,主要涉及强度退化、累积损伤等因素,近年来国内外学者纷纷从概率、模糊及非概率的角度揭示其演变过程。王新刚等[1]研究了变幅随机载荷和强度退化下结构的动态可靠性问题。秦大同等[2]建立随机风引起的系统外部载荷激励作用下的风力发电机传动系的动态可靠性模型。方永锋等[3]运用Turkstra方法分析了4种随机应力组合作用,以及结构强度不退化和退化下的动态可靠性。徐芳等[4]对外部随机风载、内部齿轮时变啮合刚度、轴承时变刚度及综合传递误差等耦合进行研究,并得出失效相关性和强度退化对可靠度的影响规律。HAJIALIZADEH等[5]研究了载荷的空间以及剩余强度变化下桥梁的动态可靠性评估。王磊等[6]将模糊变量进行等概率当量转换,建立了模糊动态可靠性分析模型。高明君等[7]提出了一种模糊动态可靠性的建模方法。概率或模糊动态可靠性模型的求解主要基于Monte Carlo方法、静态转换和跨越率方法。张宇贻等[8]运用Monte Carlo方法计算了平稳二项动载和随机恒载联合作用下的时变可靠度。HU等[9]对时变可靠度问题进行时不变转换和求解,提高了计算效率。MOURELATOS等[10]结合随机振动理论、总概率定理及使用向上跨越和接合点向上跨越率积分方程进行振动梁的动态可靠性研究。
概率或模糊方法均需依赖大量的原始数据。工程实际中往往难以获得参数的精确值,但其界限较易确定。近年来,区间方法成为处理有界不确定问题的有效途径。姜潮等[11]针对概率与区间混合不确定问题,构造一种含区间变量的动态可靠性分析方法。魏宗平等[12]提出了随载荷作用次数而变化的区间动态可靠性指标计算方法。方永锋等[13]研究了阶梯型、等幅交变型和任意时变型三种载荷作用下结构的区间动态可靠性。张德权等[14]基于PHI2提出了一种求解算法,可获得设计周期内的可靠性区间。
考虑到可靠性随载荷作用次数的影响,人们进行了进一步研究。方永锋等[15]对多次区间载荷进行当量标准正态化处理,将区间随机可靠性问题转化为随机可靠性问题求解。王正等[16]运用概率微分方程和全概率公式建立了随机载荷反复作用下的动态可靠性模型,为准确评估可靠性提供了方法,但计算的是最大载荷下的可靠度。以上研究均未考虑不同级别的载荷作用次序而导致的非线性疲劳损伤对可靠性影响的差异,因此预测结果存在较大误差[17]。
本文在现有动态可靠性理论的基础上,研究不同级别载荷的不同作用次序而导致不同疲劳累积损伤的等效转化问题,为多级载荷累积损伤下结构的动态可靠性分析提供模型和方法。
1 剩余强度的描述及其退化模型
当强度指标(如疲劳强度)在载荷作用的整个过程中不断变化时,系统的可靠性建模应当考虑强度退化的影响。以疲劳失效问题为例,强度指标随着载荷作用次数的增加而逐渐减小,即剩余强度不断减小。通常,强度退化与载荷幅值、作用次数以及加载顺序等因素有关。
材料的强度在实际工作中有一个随时间或载荷作用次数的增加而下降的非线性过程,即强度退化过程。剩余强度不仅与结构服役的时刻t有关,还与加载的应力水平有关,即
r(t)=f(t,sp,R) 0≤t≤T
(1)
式中,T为服役周期(周期寿命);r(t)为结构在t时刻的剩余强度,r(0)表示t=0时刻结构的强度即初始强度,r(T)表示结构服役周期T时刻的强度;sp为疲劳应力峰值;R为载荷的应力比。
载荷应力比R即为工作应力的最小值smin与最大值smax之比,其表达式如下:
(2)
载荷应力比R与服役周期T直接相关。当实际载荷的应力比变化时,根据Goodman疲劳极限图将实际载荷转化为实验载荷,再用实验s-N曲线进行疲劳寿命评估。载荷应力比R对材料的强度退化系数γ(γ>0)也产生直接影响,姚卫星[18]对相同材料在不同载荷应力比R下强度退化系数γ的变化情况进行了研究。显然,载荷应力比R对剩余强度的影响可纳入服役周期T及材料强度退化系数γ两个参数中。
根据热力学的观点,损伤是不可逆的,对疲劳过程中强度的退化模型来说,剩余强度是单调递减的函数。SCHAFF等[19]提出在常幅载荷作用下,剩余强度按幂指数规律变化,其关系表达式如下:
(3)
对于不同材料,其剩余强度退化规律不同,强度退化系数γ的取值就存在差异。当γ取不同值时,剩余强度曲线也不同,如图1所示。由图1可以看出,当γ=1时,式(3)退化成线性规律形式;当γ>1时,r(t)呈现开始阶段退化较慢,后期迅速下降的特点;当γ→∞时,r(t)退化成折线式规律形式。对于金属材料,从疲劳机理上看,在疲劳加载初期,元件在疲劳载荷作用下产生的缺陷如位错、滑移、空洞等对元件强度的影响较小,剩余强度衰减得较慢,但在后期其缺陷如裂纹将使元件强度迅速减小,从而产生破坏现象,故金属材料的强度退化系数γ>1。

图1 剩余强度退化规律Fig.1 The law of residual strength degradation
2 多级载荷下疲劳损伤累积规律与剩余强度
累积损伤规律是疲劳研究中的关键问题之一。线性疲劳累积损伤理论认为,对于任一应力水平,不论在寿命的前期或后期,每次循环的疲劳损伤量应是相等的。但事实上,疲劳损伤不是线性的,要想较好地反映结构件的真实可靠性,需合理考虑非线性疲劳损伤累积规律。
有限寿命设计法主要基于疲劳累积损伤理论。可以证明,式(3)必定满足下列两个边界条件:
r(0)=σb
(4)
r(T)=sp
(5)
式中,σb为材料的静拉伸强度。
(6)
可以验证:
D(0)=0
(7)
(8)
可见上述定义符合损伤的一般意义,能够反映损伤演化的非线性特性。
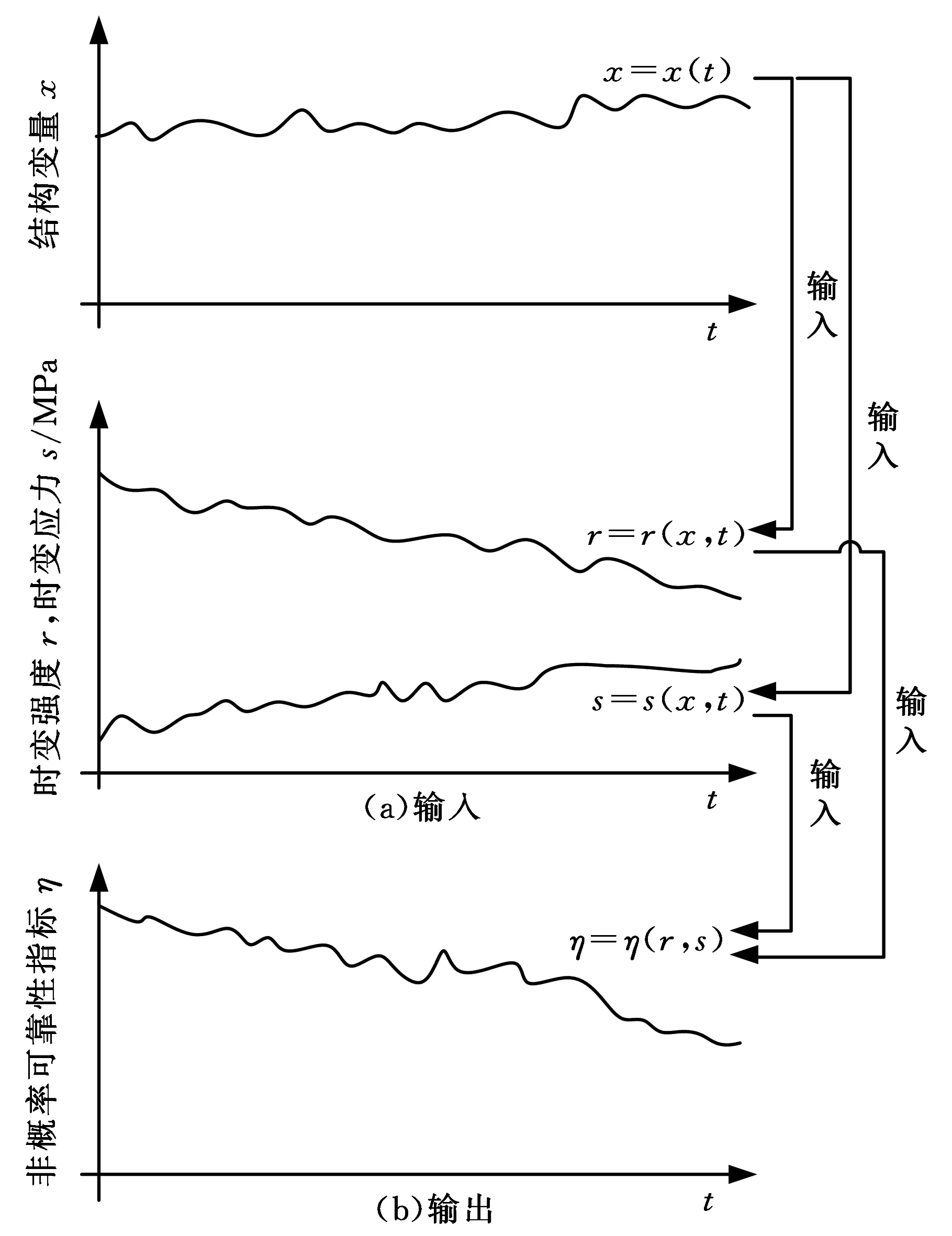
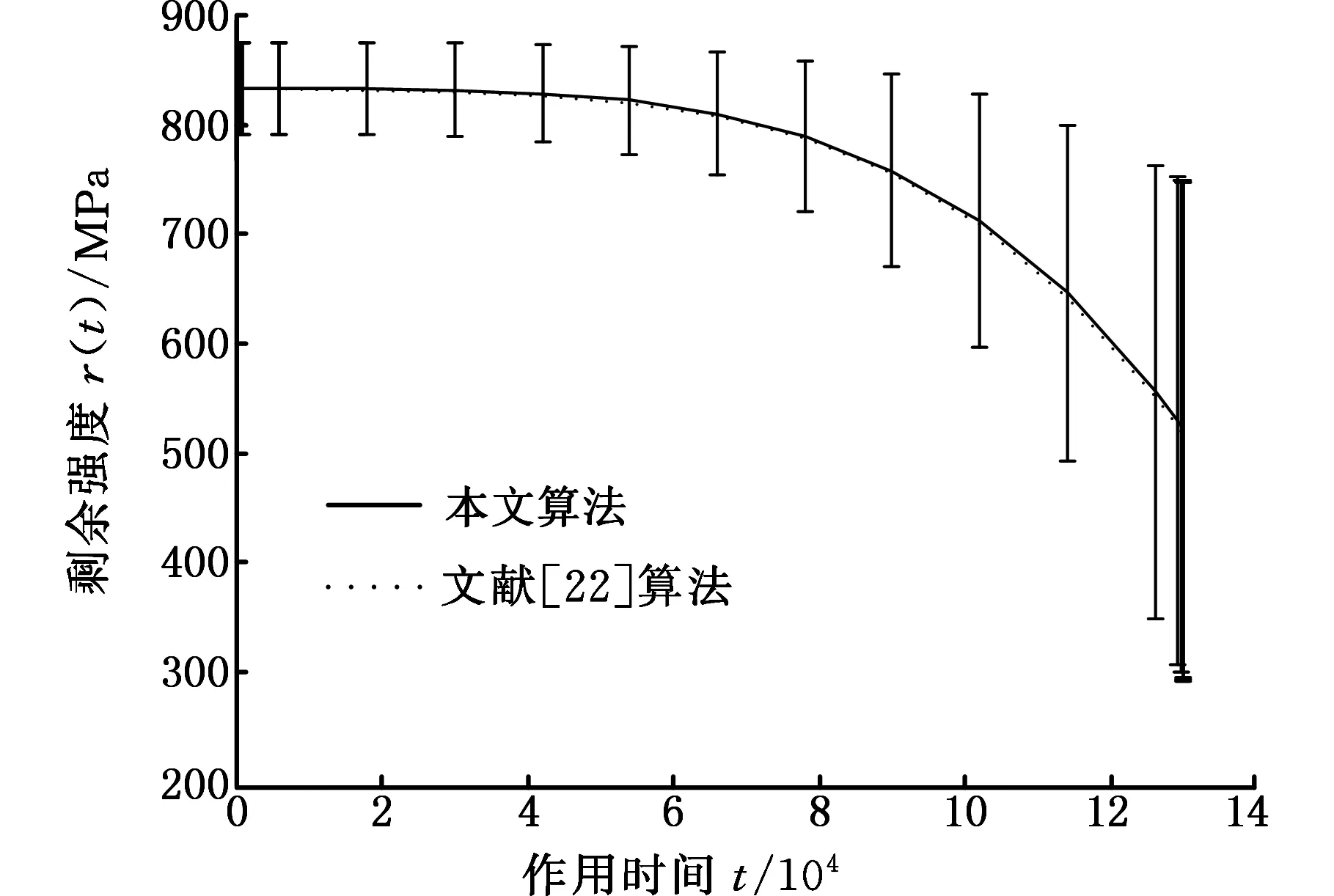
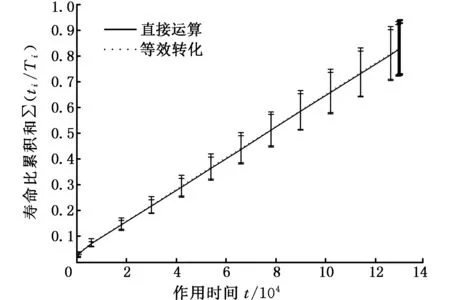
图2中,OA和OBC分别为在应力峰值sp1和sp2作用下,材料发生的损伤量随作用时间的变化曲线,其对应的服役周期分别为T1和T2。对于金属材料,当sp1>sp2时,T1 (a)高-低载荷顺序 (b)低-高载荷顺序图2 两级载荷顺序的疲劳损伤演化规律Fig.2 Fatigue damage evolution law of two levelloading sequence 由图2可以看出,材料在sp1下作用时间t1和在sp2下作用时间T2-t2的疲劳损伤量相等。根据式(8)可得 (9) 可简化为 (10) (1)高-低顺序加载时,有sp1>sp2,γ1<γ2,故 (11) 结合式(10),则 (12) 故 (13) (14) 假设结构承受两级载荷,在一级应力sp1作用时间t1后,根据疲劳损伤量等效等值寿命原则,可换算成二级应力sp2的等效作用时间t21,推导如下: 因为 所以 (15) 显然,结构受一级应力和二级应力作用之后,产生的损伤量等效于原结构在二级应力下连续作用时间t21+t2产生的总损伤量,即 (16) 则结构受一级应力和二级应力作用之后,转化为二级应力下的剩余寿命为 (17) 在二级应力下作用时间t2后,根据疲劳损伤量等效等值寿命原则,可换算成三级应力的等效作用时间t32,推导如下: 因为 所以 (18) 同理,可推算出第i级应力spi的等效作用时间ti(i-1)为 (19) i=1,2,…,n 式中,ti-1为第i-1级应力sp(i-1)的等效作用时间;t(i-1)(i-2)为第i-1级应力的等效作用时间;Ti-1为结构在应力sp(i-1)作用下的生命周期。 根据式(3),可计算出第i级应力的等效作用时间下的剩余强度为 (20) (21) (22) 在实际服役过程中,受结构自身的材料性能、使用时间、荷载效应以及所处环境等因素影响,强度r和应力s都是一个动态的过程,随时间与结构参数变化,且强度和应力为区间变量,同时因强度和应力还随着疲劳载荷作用的次数或时间而变化,故强度和应力的区间范围也在不断变化。强度r和应力s可表示为t与x的函数: r=r(x,t)∈rI(x,t)=[rl(x,t),ru(x,t)] (23) s=s(x,t)∈sI(x,t)=[sl(x,t),su(x,t)] (24) 式中,ru(x,t)、rl(x,t)、su(x,t)、sl(x,t)分别表示结构时变强度r(x,t)和时变应力s(x,t)的上下界。 图3所示为考虑结构抗力与荷载效应的时变性,用区间模型来描述不确定性变量的结构时变非概率可靠性分析的输入和输出过程。 图3 时变可靠性分析的输入和输出Fig.3 Input and output of time-dependent reliability analysis 当考虑结构荷载效应与抗力的时变性时,基于应力-强度干涉理论,以应力极限状态表示的结构动态功能函数为 M=f(x,t)=g(r(x,t),s(x,t))=r(x,t)-s(x,t) (25) 由区间非概率可靠性定义式,可推导得出在t时刻结构处于安全状态即M>0的非概率可靠性指标为 (26) (27) (28) (29) (30) 式中,rc(x,t)、rr(x,t)分别为时变强度区间变量的中心和半径;sc(x,t)、sr(x,t)分别为时变应力区间变量的中心和半径。 当仅考虑强度随作用时间衰减时,时变强度r(x,t)可以用r(t)代替,式(26)可简化为 (31) (32) 结构剩余强度的中心和半径分别为 (33) 则非概率可靠性指标η为 (34) M=sp-s(x,t) (35) 在t时刻结构处于安全状态即M>0的非概率可靠性指标η为可表示为 (36) 根据非概率可靠性指标的概念[21],η的值越大,结构安全程度越高。当η>1时,结构安全可靠;当η<-1时,结构必然失效;当-1<η<1时,结构可能安全,也可能失效;当η为1和-1时,结构分别处于必定安全可靠和必定失效的临界状态。 预测模型 基于应力-强度干涉理论,以应力极限状态表示的结构在ti时刻的动态功能函数为 M=g(r(x,t),s(x,t))=r(x,t)-s(t)= (37) (38) (39) 则非概率可靠性为 (40) 算例研究材料为45钢拉伸样件在三级载荷作用下的疲劳拉伸动态可靠性。为便于对本文提出的多级载荷作用下结构动态非概率可靠性预测模型与方法进行对比分析与评估,选用文献[18,22]中部分数据,对结构在一、二、三级载荷下的服役周期T1、T2、T3的区间宽度进行设置,根据“常见通用设备经济寿命参考年限表”中经济寿命上下界关系[23],区间上界值约为下界值的125%。具体如下:r(0)=[791.92,875.28]MPa,先在第一级载荷应力区间[301.15,332.85]MPa下作用t1=640次循环,T1=[29 025,35 722],γ1=4.092。再在第二级载荷应力区间[285,315]MPa下作用t2=1 000次循环,T2=[64 116,80 812],γ2=4.121。最后在第三级载荷应力区间[264.1,291.9]MPa下作用t3=6 000,18 000,30 000,42 000,54 000,66 000次循环,直至达到安全临界状态,T3=[145 971,185 607],γ3=4.186。 根据式(6),在第一级载荷应力区间[301.15,332.85]MPa下作用t1=640次循环,产生损伤量: (41) 则在第一级载荷作用时间t1=640次循环后,剩余强度为 (42) 由式(27)~式(30),计算可得rc(t1)=833.599 9、sc(x,t)=317,rr(t1)=41.680 0、sr(x,t)=15.85,根据式(26),非概率可靠性指标为 η=8.979 7 (43) 根据式(15),将一级应力sp1作用时间t1等效换算成二级应力sp2的等效作用时间t21: t21=[1 111.8,1 899.7] (44) 本文计算的区间结果t21=[1 111.8,1 899.7],该区间上下界的几何平均数为1 453.3。而文献[22]模型计算的t21=1 454次。显然1 454∈[1 111.8,1 899.7],且1 454与1 453.3非常接近,证明了本文区间模型的正确性。从区间宽度来看,参考统计学区间估计的计算,若对于样本均值为1 454、标准差为100的样本,要求置信度达到99.87%,则对应的区间估计值为[1 154,1 754],与本文运算的区间[1 111.8,1 899.7]接近程度在可接受的范围之内,表明本文运算的区间精确度可接受,在工程应用中有切实的指导价值。 显然,结构受一级应力和二级应力作用之后,产生的损伤量等效于原结构在二级应力sp2下连续作用时间t21+t2产生的损伤量,即总时间为 (45) (46) 即 (47) 结构受一级应力和二级应力作用之后,产生的总损伤量为 (48) 剩余强度为 (49) (50) 第三级载荷[264.1,291.9]MPa,T3=[145 971,185 607],γ3=4.186。根据式(18),可得三级应力等效作用时间t32: (51) 本文计算的区间结果t32=[3 833.8,916 3.8],该区间上下界的几何平均数为5 927.24。而文献[22]模型计算的t21=5 878次。显然5 878∈[3 833.8,9 163.8],且5 878与5 927.24非常接近,证明了本文区间模型的正确性。从区间宽度来看,参考统计学区间估计的计算,若对于样本均值为5 878、标准差为570的样本,要求置信度达到99.98%,则对应的区间估计值为[3 826,7 930],与本文运算的区间[3 833.8,9 163.8]接近程度在可接受的范围之内,表明本文运算的区间精确度可以接受,在工程应用中有切实的指导价值。 当t3=6 000时 (52) (53) (54) 结构受一、二级应力和三级应力作用之后,产生的总损伤量为 (55) 剩余强度为 (56) (57) 同理,计算出t3=18 000,30 000,42 000,54 000,66 000次循环直至达到安全临界状态时,结构受一、二、三级应力作用之后的非概率可靠性指标。结构受多级载荷应力作用下指标的变化情况见表1。图4所示为本文算法与文献[22]算法的剩余强度值对比。 表1 结构受多级载荷作用下的非概率可靠性指标Tab.1 Non-probability reliability index of structure under multi-level loads 图4 本文算法与文献[22]算法计算的剩余强度对比Fig.4 Compare residual strength of algorithm in this paper with the literature [22] 由表1和图4可以看出,本文算法与文献[22]算法的结果接近,文献[22]算法的结果均处于本文运算的区间内,证明了在进行多级载荷累积损伤下结构的剩余强度计算中,用区间数表达变量,经区间运算以获得区间范围,包含了计算结果所有可能的取值,这正是区间数学的特点之一。同时还可发现本文算法所得剩余强度均值略大于文献[22]算法的结果,表明文献[22]算法相对本文区间算法更偏于保守。 图5 直接运算与等效转化计算寿命比累积和对比Fig.5 Compare accumulation of the life proportion of direct operation with equivalent transformation 图6 本文计算的非概率动态可靠性指标与文献[22]计算的可靠度Fig.6 Compare non-probability dynamic reliability index in this paper with degree of reliability in the literature [22] 图6所示为本文计算的非概率动态可靠性指标与文献[22]计算的可靠度对比。由表1和图6可知,本文计算的非概率动态可靠性指标与文献[22]计算的可靠度,在第三级载荷作用下,均随着作用时间的推移呈减小趋势。由于两者的度量尺度不同(文献[22]是基于剩余强度满足正态分布的假设,根据一次二阶矩法计算出结构元件的疲劳可靠度),无法直接比较,但仍然可以对两个结果进行对比分析,了解不同度量尺度下对结构可靠度的判断以及疲劳可靠度随时间推移变化趋势上的差异。本文计算的非概率动态可靠性指标反映出,在第三级载荷作用时间达到129 972次循环时,非概率可靠性指标η=1,疲劳试样件处于安全临界状态;当载荷作用时间小于129 972次循环时,结构处于绝对安全状态。由文献[22]计算的可靠度结果可知,当第三级载荷作用时间小于90 000次循环时,结构的可靠度达到1.00,结构处于绝对安全状态;而当载荷作用时间大于90 000次循环时,结构的可靠度持续减小,在载荷作用时间达到129 972次循环时,可靠度仅为0.85,这也印证了文献[22]的算法对结构的可靠度判断偏于保守。此外,本文及文献[22]的结果均认为,当第三级载荷作用时间小于90 000次循环时,结构处于绝对安全状态,而当载荷作用时间大于90 000次循环时,疲劳可靠度快速减小。两者在对结构可靠度的判断以及疲劳可靠度随时间推移变化趋势上具有一致性,说明用本文建立的多级载荷累积损伤下结构的动态可靠性模型与方法是行之有效的。 (1)不同级别的载荷不同加载顺序下对结构的剩余疲劳强度将产生影响。金属材料在高-低加载时存在“过载效应”,最初施加的高载荷导致了材料的疲劳强度减小,加剧了后续施加低载荷造成的损伤,寿命比累积和将小于1;在低-高顺序加载下,由于低应力的锻炼作用,产生低载强化效果,寿命比累积和将大于1。可根据损伤等效等值寿命原则,在不同次序施加于结构的不同级别应力之间,对作用时间进行等效转化,采用高-低加载顺序时,等效转化运算对剩余寿命的预测将更偏于保守,低-高顺序加载则相反。 (2)利用区间理论,建立了动态非概率可靠性预测模型,解决了工程实际中样本数据不足条件下多级载荷累积损伤作用的结构动态可靠性预测问题,对概率与模糊的动态可靠性模型与方法进行了有益的补充。 (3)在结构的剩余强度的预测中,本文采用区间数表达变量,经区间运算以获得的剩余强度区间范围,包含了文献[22]的计算结果;同时本文运算得到的剩余强度均值略高于文献[22]的计算结果。相比文献[22],本文的结果更偏于乐观。 (4)由于度量尺度不同,无法直接比较本文计算的非概率动态可靠性指标与文献[22]计算的可靠度,但本文算法认为,算例中,当载荷作用时间小于129 972次循环时,结构处于绝对安全状态;而文献[22]算法认为在载荷作用时间达到129 972次循环时,可靠度仅为0.85。本文算法对结构的可靠性判断偏于乐观。 参考文献: [1] 王新刚, 张义民, 王宝艳. 机械零部件的动态可靠性分析[J]. 兵工学报,2009,30(11):1510-1514. WANG Xingang, ZHANG Yimin, WANG Baoyan. Dynamic Reliability Analysis of Mechanical Components[J]. Acta Armamentaril,2009,30(11):1510-1514. [2] 秦大同,周志刚,杨军,等. 随机风载作用下风力发电机齿轮传动系统动态可靠性分析[J].机械工程学报,2012,48(3):1-8. QIN Datong, ZHOU Zhigang, YANG Jun, et al. Time-dependent Reliability Analysis of Gear Transmission System of Wind Turbine under Stochastic Wind Load[J]. Journal of Mechanical Engineering, 2012,48(3):1-8. [3] 方永锋, 陈建军, 马洪波. 共同随机载荷下结构动态可靠性分析[J]. 应用力学学报,2016,33(2):345-351. FANG Yongfeng, CHEN Jianjun, MA Hongbo. Analysis of Structural Dynamic Reliability under Together Stochastic Loads[J]. Chinese Journal of Applied Mechanics,2016,33(2):345-351. [4] 徐芳, 周志刚. 随机风作用下风力发电机齿轮传动系统动载荷计算及统计分析[J]. 中国机械工程,2016,27(3):290-295. XU Fang, ZHOU Zhigang. Dynamic Load Calculation and Statistical Analysis of Gear Transmission System of Wind Turbine under Stochastic Wind Loading[J].China Mechanical Engineering,2016,27(3):290-295. [5] HAJIALIZADEH D, STEWART M G, ENRIGHT B, et al. Spatial Time-dependent Reliability Analysis of Reinforced Concrete Slab Bridges Subject to Realistic Traffic Loading[J]. Structure & Infrastructure Engineering,2015,12(9):1086385. [6] 王磊, 李林龙, 马亚飞,等. 模糊检测数据下服役钢筋混凝土桥梁的动态可靠度评估[J]. 防灾减灾工程学报,2014,34(4):529-536. WANG Lei, LI Linlong, MA Yafei, et al. Dynamic Reliability Assessment of Existing Reinforced Concrete Bridges Based on Fuzzy Inspection Data[J]. Journal of Disaster Prevention & Mitigation Engineering,2014,34(4):529-536. [7] 高明君, 张国义, 高家一,等. 基于强度退化的机构模糊动态可靠性分析方法[J]. 强度与环境,2015(1):54-62. GAO Mingjun, ZHANG Guoyi, GAO Jiayi, et al. Fuzzy Time-variant Reliability Analysis Method for Mechanisms [J]. Structure & Environment Engineering,2015(1):54-62. [8] 张宇贻, 秦权. 钢筋混凝土桥梁构件的时变可靠度分析[J]. 清华大学学报(自然科学版),2001,41(12):65-67. ZHANG Yuyi, QIN Quan. Time-dependent Reliability Analysis of Deteriorating RC Bridge Girders[J]. Journal of Tsinghua University(Natural Science),2001,41(12):65-67. [9] HU Z, DU X. A Sampling Approach to Extreme Value Distribution for Time-dependent Reliability Analysis[J]. Journal of Mechanical Design,2013,135(7):689-698. [10] MOURELATOS Z P, MAJCHER M, GEROULAS V. Time-dependent Reliability Analysis of Vibratory Systems with Random Parameters[J]. Journal of Vibration & Acoustics,2016,138(3):1-9. [11] 姜潮,黄新萍,韩旭,等. 含区间不确定性的结构时变可靠度分析方法[J]. 机械工程学报,2013,49(10):186-193. JIANG Chao, HUANG Xinping, HAN Xu, et al. Time-dependent Structural Reliability Analysis Method with Interval Uncertainty[J]. Journal of Mechanical Engineering,2013,49(10):186-193. [12] 魏宗平,李天恩. 基于强度退化分析的结构非概率动态可靠性模型[J]. 机械科学与技术,2011,30(8):1397-1401. WEI Zongping, LI Tianen. Non-probabilistic Time-dependent Reliability Model of a Structure Based on Strength Degradation Analysis [J]. Journal of Mechanical Science and Technology,2011,30(8):1397-1401. [13] 方永锋,陈建军,阎彬,等. 结构动态非概率可靠性预测模型[J]. 西安电子科技大学学报,2012,39(6):170-175. FANG Yongfeng, CHEN Jianjun, YAN Bin, et al. Model for Prediction of Structural Dynamic Non-probabilistic Reliability[J]. Journal of Xidian University,2012,39(6):170-175. [14] 张德权, 韩旭, 姜潮,等. 时变可靠性的区间PHI2分析方法[J]. 中国科学:物理学力学天文学,2015,45(5):054601-13. ZHANG Dequan, HAN Xu, JIANG Chao, et al. The Interval PHI2 Analysis Method for Time-dependent Reliability[J]. Scientia Sinica: Physica, Mechanica & Astronomica,2015,45(5):054601-13. [15] 方永锋,陈建军,阎彬,等. 多次区间载荷下结构混合动态可靠性的计算[J]. 华南理工大学学报(自然科学版),2013,41(11):91-95. FANG Yongfeng, CHEN Jianjun, YAN Bin, et al. Calculation of Structural Hybrid Dynamic Reliability under Multiple Interval Loads [J]. Journal of South China University of Technology (Natural Science Edition),2013,41(11):91-95. [16] 王正,谢里阳,李兵,等. 共因失效系统动态可靠性模型[J]. 中国机械工程,2008,19(1):5-9. WANG Zheng, XIE Liyang, LI Bing, et al. Time-dependent Reliability Model of System with Common Cause Failure[J]. China Mechanical Engineering,2008,19(1):5-9. [17] 苏志霄,刘宏昭,王建平,等. 基于剩余强度退化规律的疲劳损伤非线性演化模型[J].机械强度,2000,22(3): 238-240. SU Zhixiao, LIU Hongzhao, WANG Jianping , et al. Non-linear Model of Fatigue Damage Based on the Residual Strength Degradation Law [J]. Journal of Mechanical Strength,2000,22(3):238-240. [18] 姚卫星. 结构疲劳寿命分析 [M].北京:国防工业出版社,2003. YAO Weixing. The Statistical Analysis of Structure Fatigue Life [M].Beijing: National Defence Industry Press,2003. [19] SCHAFF J R, DAVIDSON B D. Life Prediction Methodology for Composite Structures. Part I--Constant Amplitude and Two-Stress Level Fatigue[J]. Journal of Composite Materials,1997,31(2):158-181. [20] 储军,郑松林. 谱载荷下加载次序效应定量评价的初步研究[J]. 中国机械工程,2015,26(3):365-368. CHU Jun, ZHENG Songlin. Preliminary Study of Quantitative Evaluation for Spectrum Load Sequence Effect[J]. China Mechanical Engineering,2015,26(3):365-368. [21] 郭书祥,吕震宙,冯元生. 基于区间分析的结构非概率可靠性模型[J]. 计算力学学报,2001,18(1):56-60. GUO Shuxiang, LYU Zhenzhou, FENG Yuan-sheng. A Non-probabilistic Model of Structural Reliability Based on Interval Analysis[J]. Chinese Journal of Computational Mechanics,2001,18(1):56-60. [22] 李少宏,陈建军,方永锋.多级载荷作用下剩余强度模型的结构元件疲劳可靠性分析[J].机械科学与技术,2013,32(6):791-795. LI Shaohong, CHEN Jianjun, FANG Yongfeng. Analysis of the Fatigue Reliability for Structural Element under Multi-level Loads Based on the Residual Strength Model[J]. Mechanical Science & Technology for Aerospace Engineering,2013,32(6):791-795. [23] 编委会.最新资产评估常用数据与参数手册2010~2011年[M].北京:经济科学出版社, 2010. Editorial Board. The Latest Commonly Used Data and Parameters Manual of Asset Evaluation for 2010-2011 [M]. Beijing: Economic Science Press,2010.


3 基于区间分析的动态非概率可靠性指标


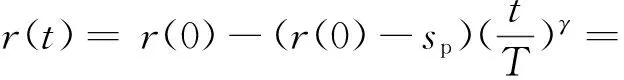
4 多级载荷作用下结构动态非概率可靠性

r(ti(i-1)+ti)-spi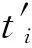
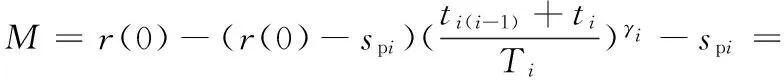

5 算例
5.1 第一级载荷作用
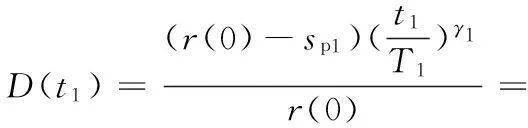

5.2 第二级载荷作用
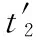
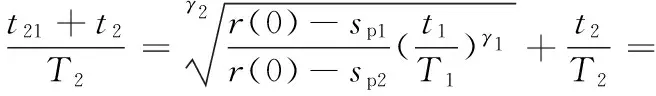
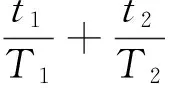

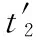
5.3 第三级载荷作用
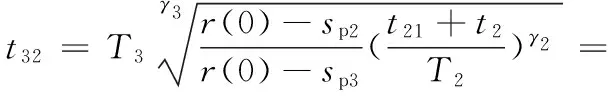
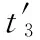
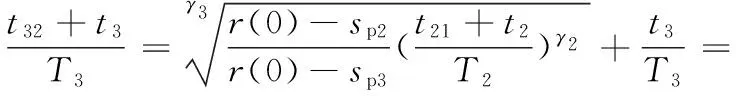
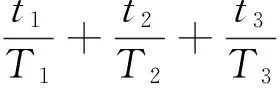

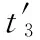



6 结论

