基于自导向副弹塑性变形的深孔轴线偏斜研究
庞俊忠 李鹏飞 黄晓斌
中北大学机械工程学院,太原,030051
0 引言
在机械加工行业,深孔加工是一种较为重要的加工方式。随着机械工业的发展和制造工艺的提高,深孔加工技术在诸多行业中得到了广泛的应用,同时高精、高质深孔的加工也越来越多,但始终存在一个重大问题困扰着深孔加工制造业,即深孔钻削中的孔轴线偏斜,因此开展孔轴线偏斜问题的研究具有现实意义[1]。
深孔轴线偏斜是一个复杂的动力学问题,并且随着加工深度的增加,偏斜量是一个逐渐扩大的过程,如果加工过程不对初始偏斜进行矫正,孔轴线偏斜量会随着孔深的加大而增大。国内外学者对孔轴线偏斜问题进行了研究。BIERMANN等[2]根据拓扑优化原理,对刀具进行切削力优化,以增大BTA深孔钻的排屑口,改善了排屑效果; AL-HAMDAN[3]研究了工件旋转轴线和刀具中心有不同误差时对切削力和扭矩的影响,结果显示,误差越大,影响越大;杨样等[4]研究了枪钻加工深孔时提高深孔直线度的方法,主要针对加工的稳定度进行了分析研究。
这些研究多集中于深孔表面粗糙度、圆度、直线度控制、系统振动等,没有考虑刀具的自导向特征。所谓自导向,就是刀具不借助外加导向定位装置就可依靠自身导向条与已加工孔的表面形成导向副,以已加工孔壁作为导向。这种导向副和通常所说的机床上的导轨副作用是类似的,在轴线方向可以把已加工孔壁看成固定导轨,导向条看成移动导轨,但固定导轨的材料和状态是由被加工工件决定的,不同的工件材料机械性能差别很大,与导向条接触的已加工孔壁弹塑性变形将极大地直接影响深孔轴线的偏斜,导致进出口偏差。由于工件的材料状态无法改变,故刀具导向条和刀刃的结构及几何参数、刀具工作条件等对深孔轴线的偏斜造成决定性的影响。
本文根据工件材料、钻孔直径、刀刃几何参数等,建立了自导向刀具的受力模型。基于深孔刀具的自导向机理,借助Hertz接触理论,结合钻削实验得到的深孔偏斜数据,建立了一个预测深孔轴线偏斜的数学模型,并依据该模型分析了导向条滞后量对轴线偏斜的影响。
1 自导向刀具偏斜分析
孔轴线的偏斜,不管影响因素有哪些,在稳定切削的情况下,最终都必须通过自导向副来起作用,这是自导向深孔刀具的根本特点。如图1所示,导向条与工件内壁相接触的切线为导条接触线,假设刀具为理想的刚性体,在正常工作状态,刀具工作的理想轴线会与导条接触线始终保持平行。实际工作中,由于各因素的综合影响会导致导向接触线发生偏斜,进而造成深孔刀具发生轴线偏斜,即导向条接触线决定了刀具轴线的状态[5]。因此,导向副的工作状态是决定自导向刀具是否发生轴线偏斜的根本原因。
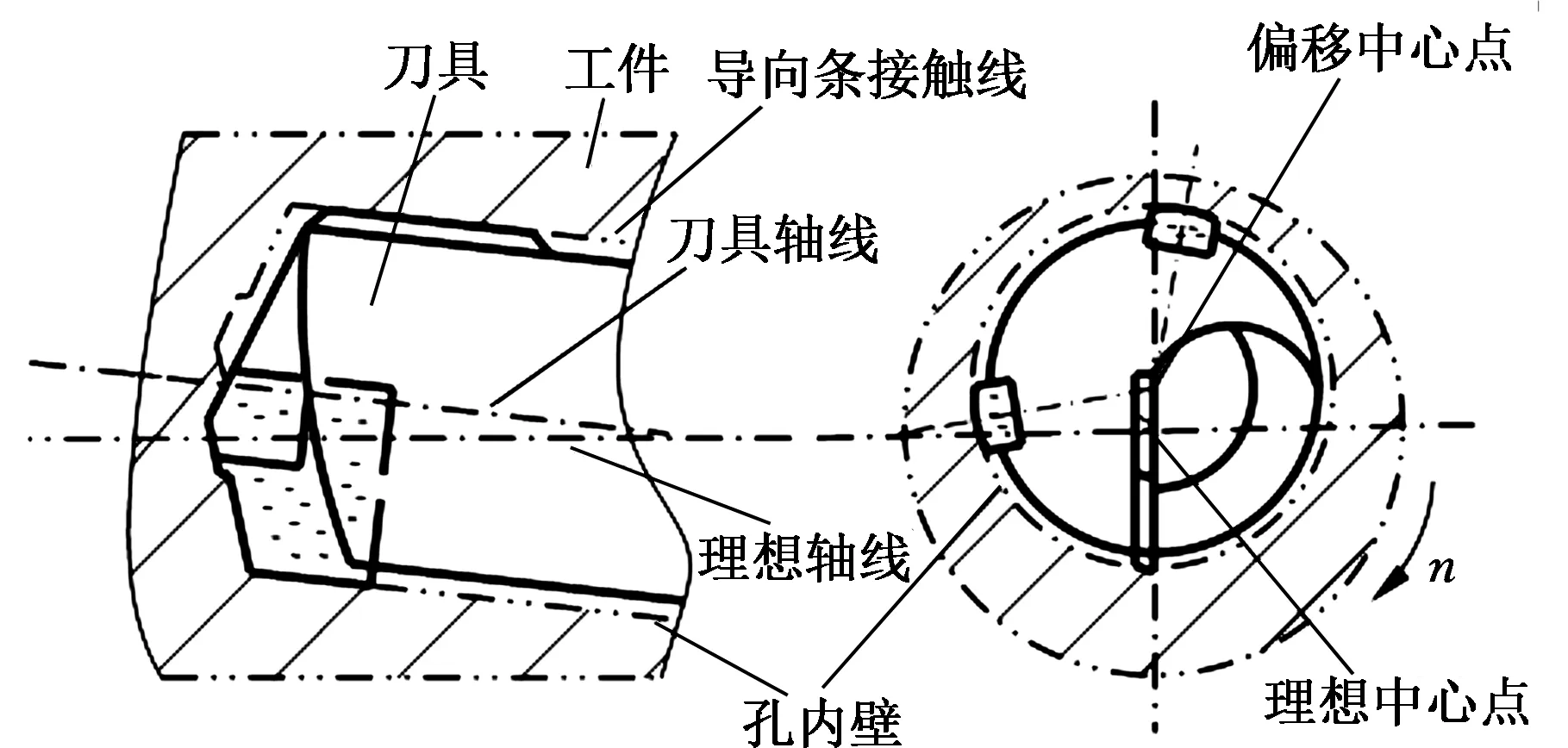
图1 刀具轴线偏斜图Fig.1 The axis deflection diagram of tool
2 BTA深孔钻导向副分析
2.1 导向副受力计算
对自导向刀具的导向副状态进行深入研究,建立导向副的受力模型,如图2所示,导向条1、2分别受到正压力FG1、FG2,以及正压力引起的摩擦力μFG1、μFG2。
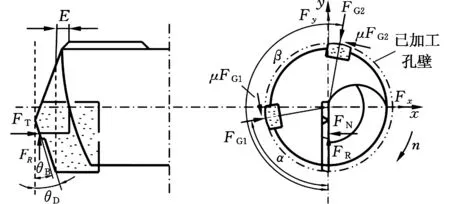
图2 单齿BTA深孔钻受力图Fig.2 Drilling force diagram of single tooth BTA deep hole drill
根据受力模型可计算出稳定切削状态下导向条1、2上所受的正压力:
(1)
式中,Fx=-FN,FN为刀齿的主切削力;Fy=FR,FR为刀齿径向切削力;α、β为导向条的位置角,α=85°±5°,β=183°±5°,本文取α=90°,β=180°;μ为摩擦因数。
2.2 导向副载荷形式分析
研究自导向刀具的轴线偏斜首先需要深入分析导向副的受力状态,在此基础上建立导向副的偏斜模型[6]。在稳定切削阶段,对导向条及其一侧的刀体进行受力分析,导向条承受来自工件内壁的正压力FGi(i=1,2),以及一侧的刀体承受支撑力F,两力的方向相反,大小相等,即|F|=|FGi|(i=1,2)。设导向条的长度为2L,导向条的滞后量为E,如图2所示,力的支点为“Δ”,如图3所示。力F对支点“Δ”会产生力距M,为使刀体同时达到力和力矩平衡,则导向条上必然有载荷作用,由力平衡可知导向条受到均布载荷q1作用,如图3a所示;又由力矩平衡可知导向条受到分布载荷q2作用,如图3b所示,因此导向条所受的载荷为q1和q2的叠加。
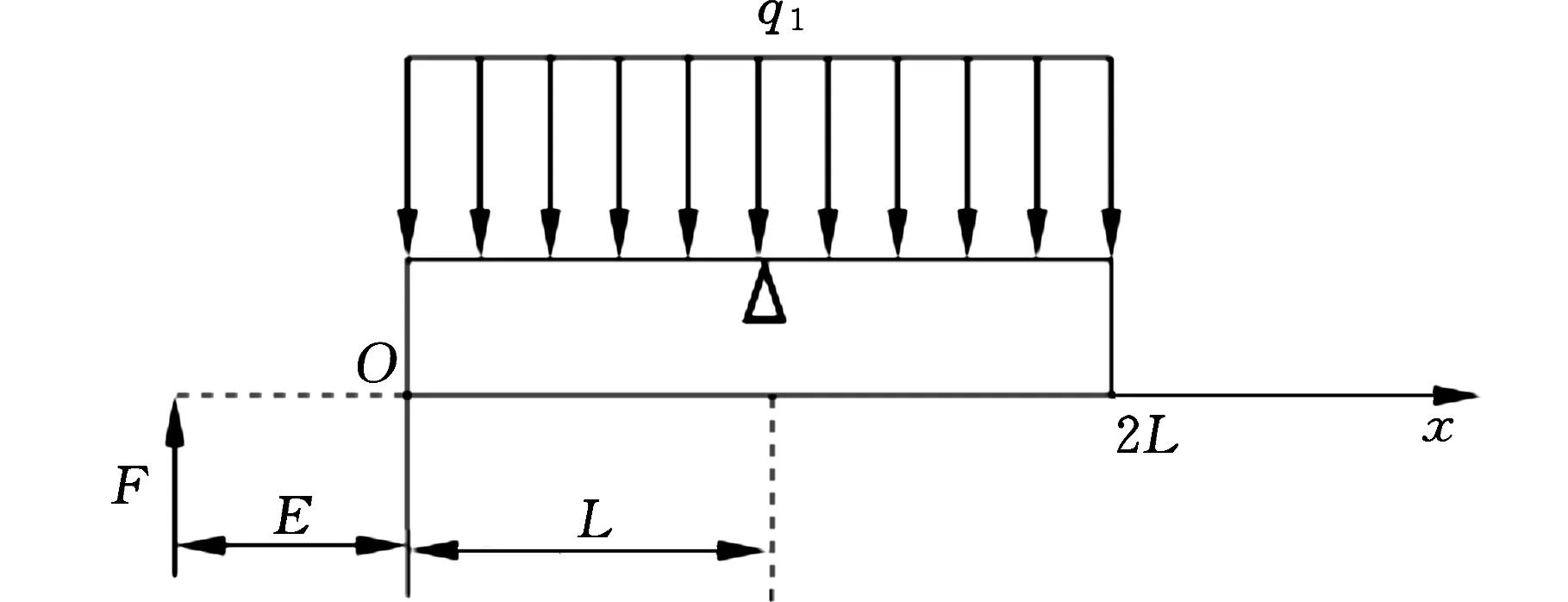
(a)均布载荷
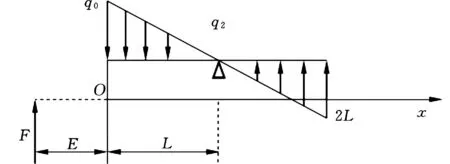
(b)对三角分布载荷图3 导向条载荷图Fig.3 The load diagram of guide bar
根据平衡条件可得
(2)
由M=F(E+L),解得
(3)
因q2(x)为线性载荷,可将其设为
q2=kx+q0
(4)
根据载荷q2(x)施加在导向条上的特殊性,可知q2(L)=0,解得
(5)
综合式(3)~式(5),可求得
(6)
因导向条上施加有载荷q1和q2,则其总载荷q为q1与q2的矢量和,即q=q1+q2,针对导向条上的载荷q,分析可知导向条存在如下三种受力状态:
(1)当|q1|>|q0|时,导向条在其长度2L上,载荷q方向均向下,呈全覆盖梯形分布,实际接触长度l′=2L,如图4a所示;
(2)当|q1|=|q0|时,导向条在其长度2L上,载荷q方向均向下,且q(2L)=0,整体呈全覆盖三角形分布,实际接触长度l′=2L,如图4b所示;
(3)当|q1|<|q0|时,导向条上载荷局部覆盖,方向向下,呈局部三角形分布,实际接触长度l′<2L,如图4c所示。
综上所述,导向条上总载荷的分布形式与载荷q1和q2有关,因其大小不同造成载荷的分布长度不同,总体上是|q1|相对于|q2|的值越大,载荷覆盖长度越大。此外,由于力的相互作用,可认为导向条对于工件内壁的载荷形式与其作用在导向条上的载荷形式是相一致的,仅在方向上相反。
3 导向副弹塑性理论接触模型建立
3.1 导向副接触模型建立
在深孔加工过程中,由于导向条与工件内壁存在接触力,因而会发生接触变形。在接触的初始阶段,导向条的宽相对于工件内壁有限,因此初始接触可看作是一条线,随着两者的相对运动以及接触深入,导向条与工件内壁的接触由线接触扩展到窄面的接触,接触模型如图5所示。
3.2 接触变形理论分析
导向条与工件内壁的初始接触类似于线接触,接触过程可分为弹性接触和塑性接触两个阶段,则接触变形量应为弹性变形和塑性变形之和。
弹性接触阶段的接触变形可结合Hertz接触理论,采用Palmgren给出的关于线接触弹性变形计算公式[7]:
(7)
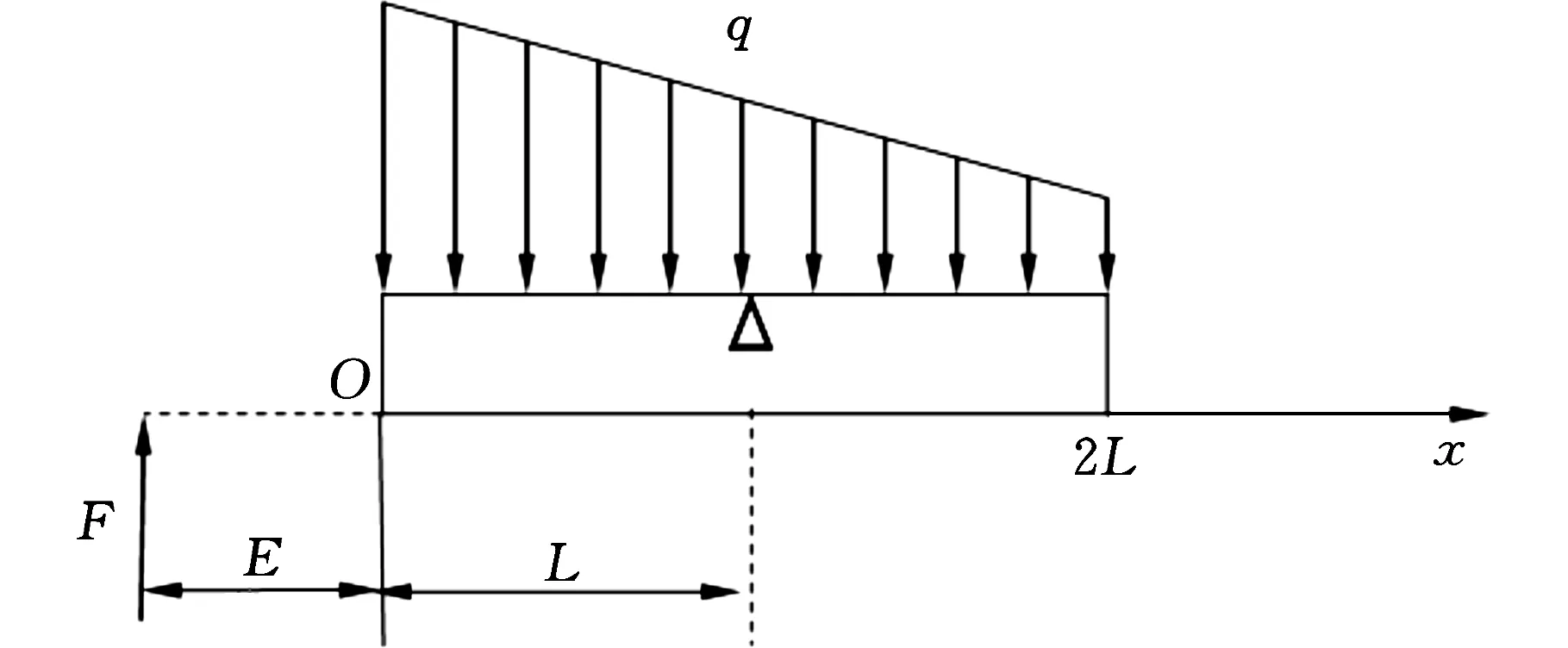
(a)梯形载荷全覆盖
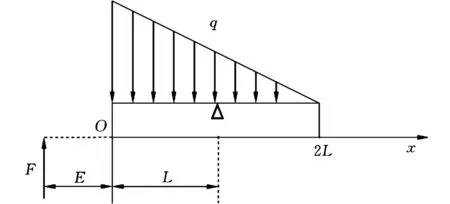
(b)三角形载荷全覆盖
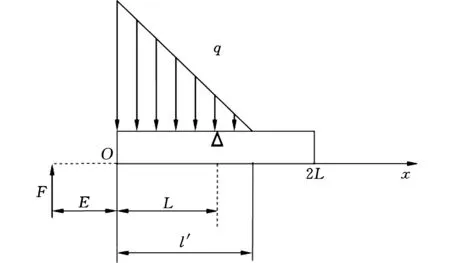
(c)三角形载荷局部覆盖图4 导向条载荷分布形式Fig.4 Distribution form of guide bar load
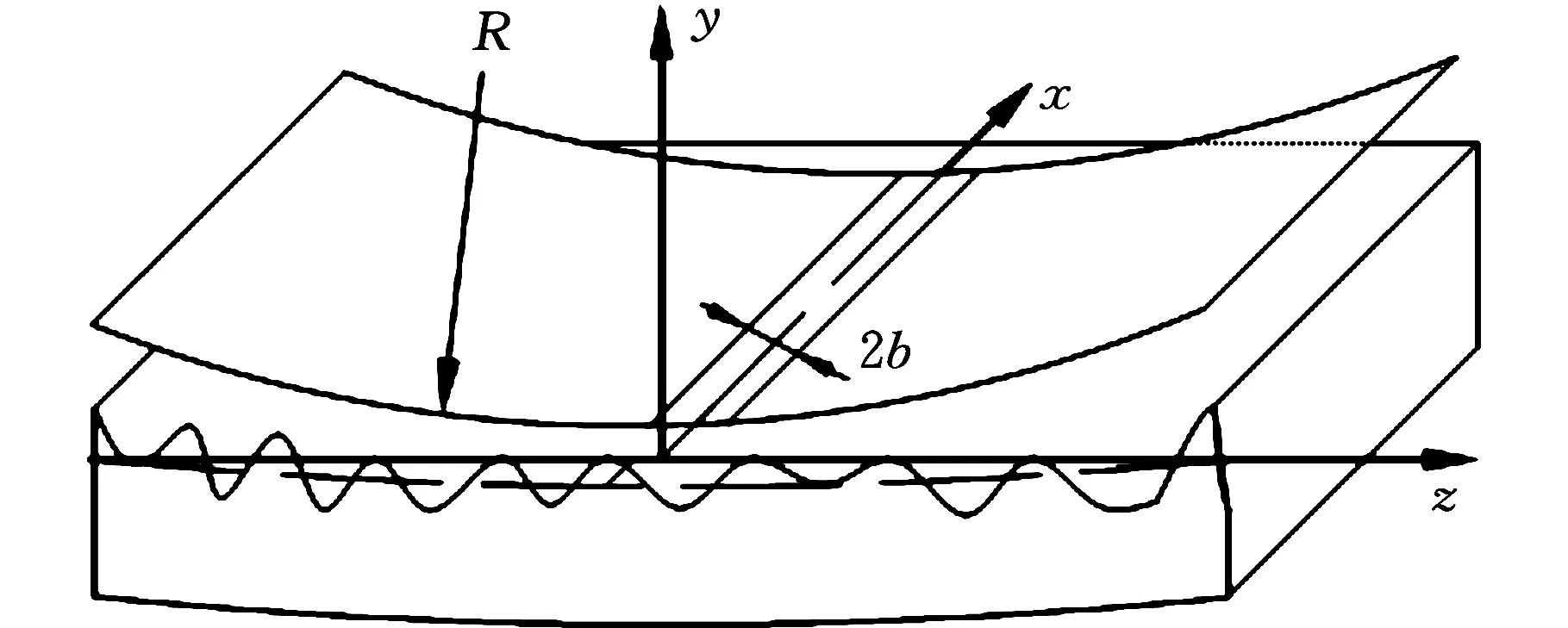
图5 导向副接触模型Fig.5 The contact model of guide bar
式中,η为两接触体综合弹性常数;E1、E2分别为两接触体的弹性模量,Pa;ν1、ν2为泊松比;PL为法向线接触载荷,N;l为接触线长,m。
塑性接触阶段的接触变形遵循Mises屈服准则,参考倪艳光等[8]推导的过载工况下的线接触永久变形计算理论,推得材料的临界变形量
(8)
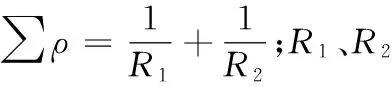
材料屈服极限的临界载荷
(9)
线接触的塑性变形量
(10)
导向副的接触变形为弹性变形和塑性变形两者之和,即δi=δt+δs(i=1或2,分别表示导向条1、2),整理可得总变形量
(11)
4 实际接触载荷及偏斜量分析
4.1 实际接触变形
理论接触载荷模型是单位载荷在线性接触的基础上建立的,但随着加工的深入,接触形式有向面接触发展的趋势,则在接触长度内的单位载荷会发生变化,在切削加工的稳定阶段,在一定程度上可视为窄面接触。现对理论接触载荷计算公式进行修正,引入接触宽度系数kb,可表示为
(12)
式中,bs为实际接触宽度;b为名义接触宽度。
实际载荷与理论载荷关系为
(13)
用实际接触载荷Pb替换式(7)、式(11)中的PL,实际接触长度l′代换l,可推得弹塑性阶段的实际接触变形量的计算公式:
(14)
以名义接触宽度b=8 mm例,相关系数见表1。

表1 载荷相关系数对照表
4.2 深孔轴线偏斜量分析
导向副接触过程中,由于接触载荷不同,导致工件内壁各位置的接触变形量不同,从而使导向副发生了相应的偏斜,最终造成钻孔的轴线发生偏斜,在不进行外部矫正的情况下,轴线偏斜量会随着钻削长度而增大[9]。为研究钻削过程中轴线的偏斜量,现引入单位长度偏斜量,即在单位长度上的轴线偏斜,单位偏斜量
(15)
式中,δ0为x=0时的变形量,δl′为x=l′时的变形量;i=1,2,分别表示导向条1、2。
为计算简便,导向条的位置角分别取α=90°,β=180°,则轴线总单位偏斜量
(16)
5 切削加工实验及偏斜分析
5.1 加工实验切削条件确定
为验证模型的准确性以及确定轴线偏斜形式,用φ40 mm的单齿BTA钻进行切削实验,机床为T2120深孔钻镗床,刀具材料为硬质合金,工件材料选用牌号为5052铝合金和45钢,切削实验加工孔的规格为φ40 mm×1 500 mm,工件外径为70 mm,相关材料特性见表2,刀具切削参数见表3。
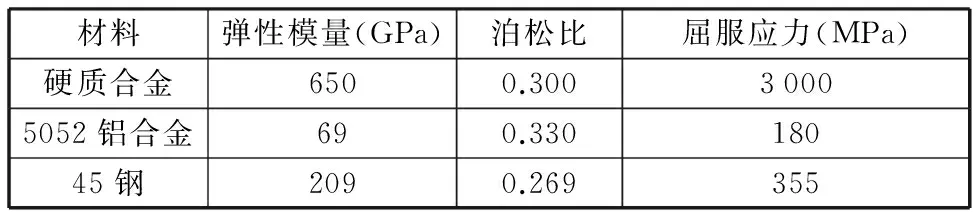
表2 接触体的材料特性Tab.2 Material properties of contact body

表3 刀具几何参数Tab.3 Tool geometry parameters
根据工件的材料特性以及刀具的切削参数选用合适的切削条件并计算切削力,切削用量及切削力参数如表4所示。
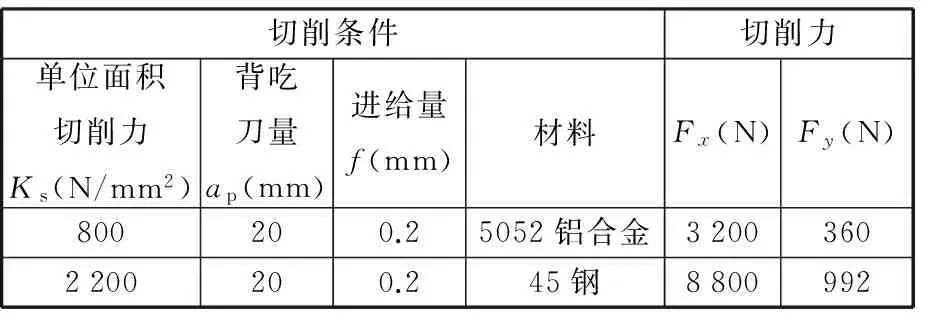
表4 切削用量及切削力参数Tab.4 Cutting amount and cutting force parameters
5.2 轴线偏斜分析
根据表2的材料特性、表3的刀具材料切削参数以及表4的切削用量和切削力参数,运用式(1)、式(6)可解得导向副接触线长l=18.975 mm<30 mm,载荷为局部三角形覆盖;运用式(1)、式(14)~式(16)可计算不同载荷下的理论轴线总偏斜量,如表5所示。
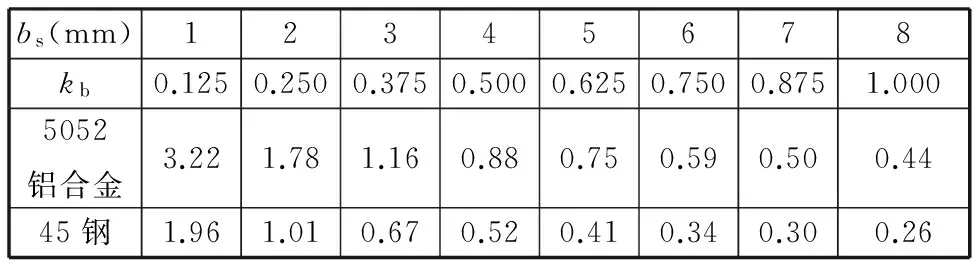
表5 不同载荷下的理论单位长度总偏斜量Tab.5 The total deflection of theoretical unitsunder different loads mm/m
分别加工20根试件,通过测量壁厚差来计算轴线偏斜,在已加工工件的出口端分别取8个点进行测量,将壁厚的最大值与最小值作差除以2作为出口偏差值,钻削后的试件见图6,工件实际单位偏斜量分布如图7所示。

(a)入口端 (b)出口端图6 深孔试件Fig.6 Test artifact of deep-hole
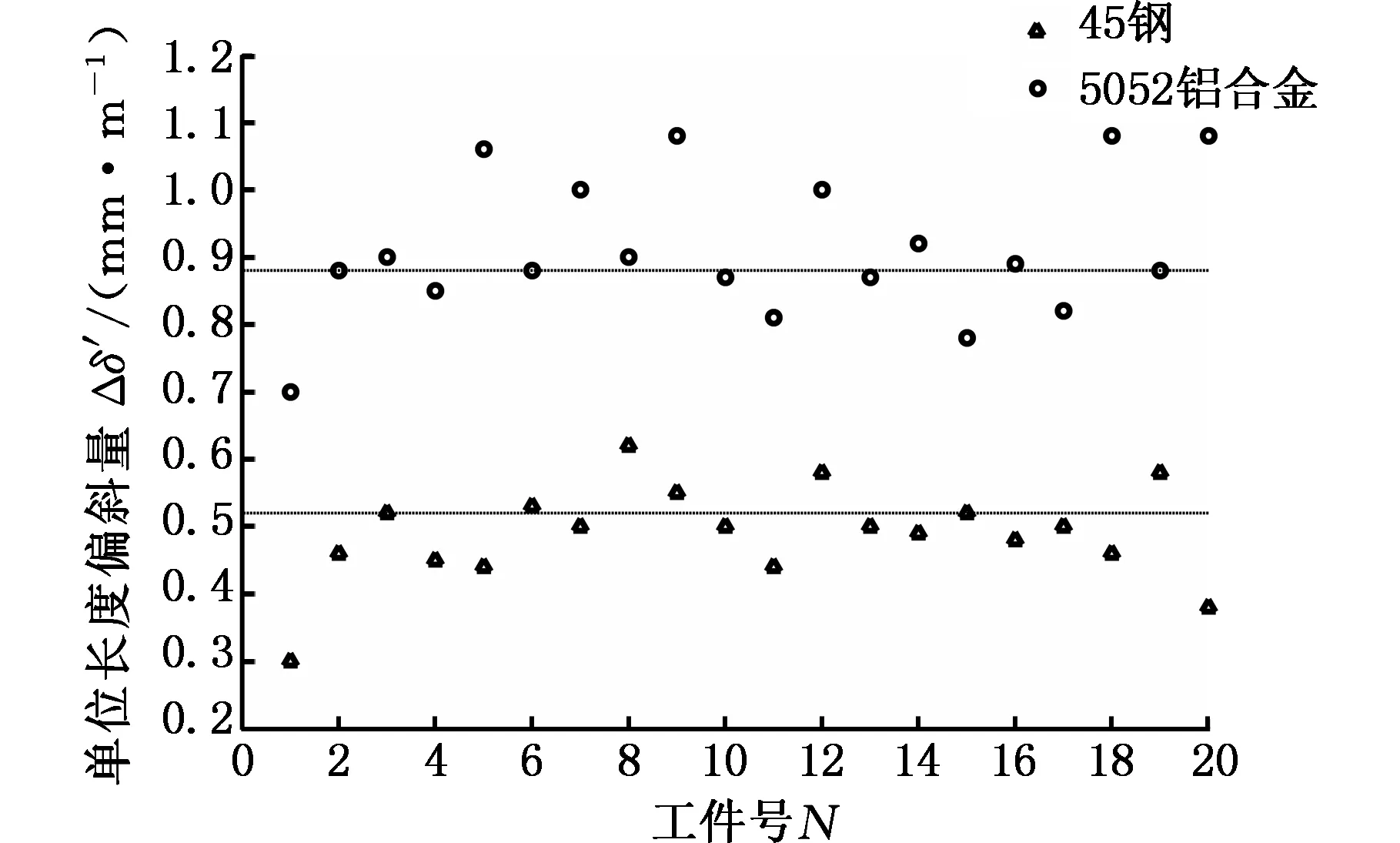
图7 工件轴线单位偏斜量分布Fig.7 Unit deflection distribution of workpiece axis
将表5的理论轴线单位偏斜量与图7实际工件轴线单位偏斜量进行对比分析,可得出如下结论:导向条滞后量E=0.5 mm,名义接触宽度b=8 mm,导条长度2L=30 mm时,工件的轴线单位偏斜量与实际接触宽度bs=4 mm、kb=0.5时的理论轴线总单位偏斜量相吻合,此时导向副实际接触线长为18.975 mm<30 mm,即载荷为三角形局部覆盖,实际接触宽度为名义宽度的一半。
5.3 滞后量对导向副变形量的影响
根据实验对比得到的理论模型来探讨导向条的滞后量对于导向副变形量的影响,针对第1根导向条,在其实际接触长度l′=18.975 mm,实际接触宽度bs=4 mm不变的情况下,改变滞后量E的大小,导向副变形量如图8所示。
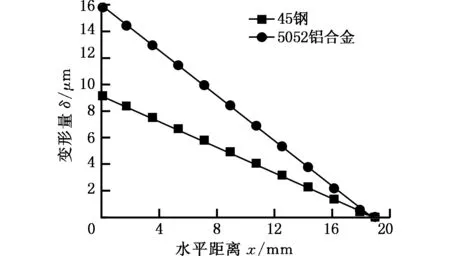
(a)E=0.5 mm
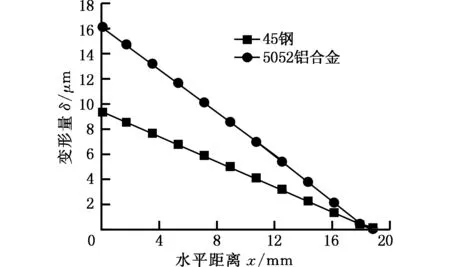
(b)E=1.0 mm
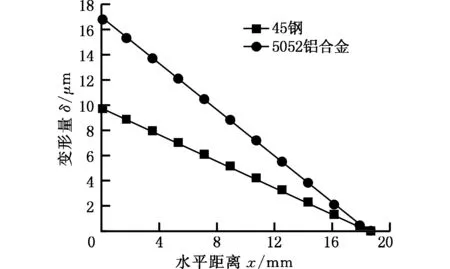
(c)E=2.0 mm
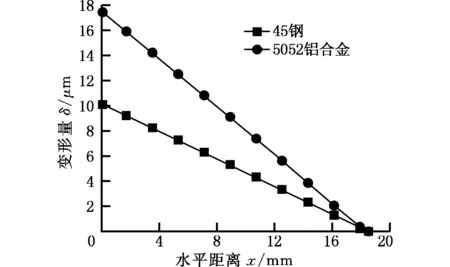
(d)E=3.0 mm图8 不同滞后量下的导向副变形量Fig.8 Deformation of the guide deputy under different delayed quantity
由图8可知,随着滞后量的增加,施加在导向副上的力矩增大,为平衡力矩则导向副上各位置的接触载荷会相应增加,最终导致接触变形量有微小增大。
5.4 滞后量对轴线偏斜的影响
滞后量的改变会使导向副上各位置的变形量发生变化,将得到的变形量代入式(15)、式(16)求解钻削过程中轴线总单位偏斜量,表6为导向条长2L=30 mm、bs=4 mm的情形下不同滞后量的单位长度总偏斜量。
由表6分析可知,对于自导向深孔加工,在不改变导向条长度和接触宽度的情况下,滞后量的增加会导致轴线偏斜量增大,所以在实际钻削加工过程中滞后量越小越好,但是如果滞后量过小,导条前端的磨损会严重,缩短刀具的寿命,综合考虑到上述因素,刀具的滞后量一般取0.5~1.0 mm。

表6 不同滞后量下的单位长度总偏斜量Tab.6 The total deviation of the unit length in differentdelayed quantity mm/m
5.5 工件材料对轴线偏斜的影响
研究加工不同材料时孔的轴线偏斜,将表6的数据作图进行综合分析,如图9所示。由图9可知,在同等切削条件且导向条尺寸一致的情况下,铝合金的偏斜量比45钢偏斜量大,即材料刚度越小,孔轴线单位偏斜量越大。
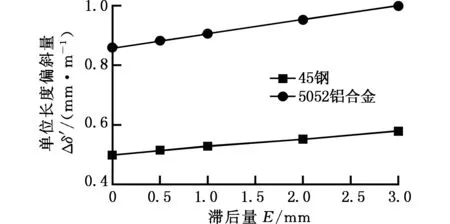
图9 不同材料下的轴线单位偏斜量Fig.9 The axis deflection of different materials
6 结论
(1)依据自导向机理,综合Hertz接触理论、弹塑性接触变形理论,建立了预测深孔轴线偏斜的数学模型,通过切削加工实例验证了该模型的准确性。
(2)导向副的接触载荷形式为局部三角形,实际接触宽度约为导向条宽度的一半。
(3)导向条的滞后量对导向副的变形量和轴线偏斜有一定的影响。在导向条长度、实际接触宽度不变的情况下,随着滞后量的增加,导向副相接触位置的变形量会有所增大,同时轴线偏斜量会相应增大。
(4)理论分析数据与实验钻削结果都证明:加工不同的材料,轴线偏斜也不相同。在同等加工条件下,因材料的机械性能不同,铝合金比45钢的偏斜量大。
参考文献:
[1] 王峻. 现代深孔加工技术[M]. 哈尔滨:哈尔滨工业大学出版社,2005.
WANG Jun.Modern Deep Hole Processing Technology[M].Haerbin: Harbin Institute of Technology Press, 2005.
[2] BIERMANN D, KERSTING M, KESSLER N. Proc-ess Adapted Structure Optimization of Deep Hole Drilling Tools[J]. Annals of the CIRP,2009,8(1):89-92.
[3] AL-HAMDAN A. Effect of Misalignment on the Cutting Force Signature in Drilling[J]. Journal of Materials Processing Technology,2002,124:83-91.
[4] 杨样,李耀明,董振.提高枪钻孔加工直线度的方法[J].工具技术,2013,47(2):23-26.
YANG Yang, LI Yaoming, DONG Zhen. Method of Improving Straightness of Gun Drilling[J]. Tool Engineering,2013,47(2):23-26.
[5] 曹利平,吴善明,王红新,等. 枪钻加工船用柴油机深孔时孔轴线偏移的机理与工艺[J]. 机械制造,2016,54(8):48-50.
CAO Liping, WU Shanming, WANG Hongxin,et al. The Mechanism and Process of the Offset of Hole Axis in the Hole of Drilling Machine[J]. Machinery,2016,54(8):48-50.
[6] 李旭波,郑建明,彭朋,等. 错齿BTA深孔钻导向条与孔壁接触状态仿真研究[J]. 机械科学与技术,2017,36(7):1042-1047.
LI Xubo, ZHENG Jianming, PENG Peng, et al. Simulation Study on Contacting State between Drilled Hole Wall and Guide Pads for Staggered Teeth BTA Drill [J]. Mechanical Science and Technology for Aerospace Engineering,2017,36(7):1042-1047.
[7] HARRIS T A. Rolling Bearing Analysis[M]. New York:John Wiley and Sons,Inc.,1991.
[8] 倪艳光,李影,邓四二,等. 过载工况下圆柱滚子轴承永久变形量计算[J]. 河南科技大学学报(自然科学版),2016,37(2):21-25.
NI Yanguang, LI Ying, DENG Sier,et al. Calculation of Permanent Deformation of Cylindrical Roller Bearing under Overload Condition[J]. Journal of Henan University of Science and Technology(Natural Science),2016,37(2):21-25.
[9] 徐光明,刘军强,高晓兵,等. 深孔加工中孔轴线偏斜的实时测量及误差分析[J]. 西安工业大学学报,2016,36(4):300-303.
XU Guangming, LIU Junqiang,GAO Xiaobing et al. Real-time Measurement of Axis Deflection in Deep Hole Machining and Error Analysis[J]. Journal of Xi’an Technological University,2016,36(4):300-303.

