基于形变模型带表情的三维人脸重建

孙建伟

（四川大学计算机学院，成都 610065）

0 引言

人脸是人脸信息传递的载体，随着近几年来生物特征识别领域的快速发展，人脸相关的研究更是成为了热门的研究对象。而真实感的三维人脸建模也逐渐成为人脸研究中一个热点问题。技术的发展，生活质量的提高，我们注意到三维人脸建模在多种领域中起着重要的作用，更是在计算机视觉、医学研究、游戏娱乐、等都具有广大的应用前景。

人脸形状建模主要有两类：一种是通过使用三维扫描设备直接建立三维模型，另一种则是根据二维图像重建出三维人脸模型。第一种建模方法采用主动式的方法获得数据，其优点是能够得到较为精确的人脸模型，但是只能在特定的环境下使用。相比较而言，第二类方法更具有普遍性，适用更多的场景，缺点就是重建的模型精度不高，推广到现实中需要一定的时间。

第二类重建方法有多种，而形变模型是第二类重建算法中的代表，它能够解决在没有任何约束下基于单张图像的三维形状重建所存在的病态问题，该方法主要依据现有的三维人脸库作为先验知识，对人脸进行约束，从而实现人脸重建。

现实中对于给定的一张人脸来说，往往带有各种表情，例如惊讶、微笑、沮丧等。这些表情的变化通常成为人脸重建中需要解决的问题。因此探索在基于形变模型的基础上添加表情模型，对带有表情的人脸进行三维重建具有重要的意义。本文就提出在基于形变模型基础上带表情的三维人脸重建，其主要思想是借助二维特征点反映的表情信息，让三维形状产生一定的形变，最终重建出人脸模型。

1 形变模型重建原理

形变模型是一种组合线性模型[1]，不同的线性组合则会重建出不同的人脸模型，其重建的过程主要分为两个阶段：一是通过获取的三维人脸原型数据建立组合模型；二是通过特定的图像实现模型的匹配。

1.1 建立组合模型

为了可以通过统一的向量形式来表示一个人脸模型，需对原型人脸进行稠密对齐，从而使得各对应三维点所代表的物理意义相同。每个三维人脸包含形状信息和纹理信息。因此，稠密对齐后的人脸模型用向量表示为：

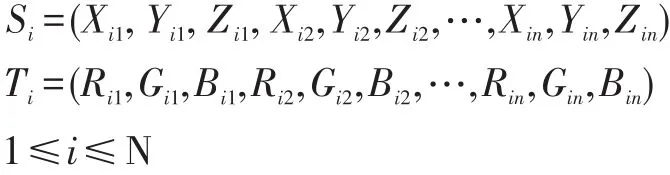
其中Si和Ti分别表示的是第i个人脸的三维形状向量以及纹理向量，N是人脸数量，n代表三维人脸点的个数。

稠密对应后的人脸向量可以通过线性表示成任何一个新的人脸模型：

其中ai，bi为组合系数，同时ai，bi各自的系数和为1。

由于原始人脸数量过多，这里我们通过主成分分析法（PCA）对形状向量和纹理向量进行转换压缩，这样不仅可以使数据量减少，而且可以消除人脸数据间的相关性[6]，经PCA变换后的组合模型可以表示为：

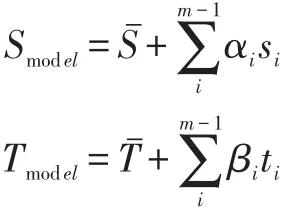
其中分别表示平均形状向量和平均纹理向量，m 是主元个数，s=（s1,s2,…，sm-1），t=（t1,t2,…，tm-1）分别是形状和纹理的主元向量组，α=（α1,α2,…αm-1）,β=（β1,β2,…，βm-1）分别代表形状和纹理向量的组合系数。通过改变上面的组合系数，可以重建出任何一个特定照片的三维人脸形状模型（Smodel,Tmodel）。

1.2 模型匹配

通过建立线性组合模型可以知道，只要求得α，β这些系数，就能表示出一张新的三维人脸模型。模型匹配就是通过求解系数α，β，从而建出三维人脸模型。这里用特定的人脸图像与模型人脸在二维图像上的投影图像对应像素的颜色信息误差的平方和最小来求解，因此得到优化函数可以表示为：

2012年6月～2017年6月，在本院骨关节科接受Oxford活动平台内侧单髁（Biomet,USA）置换的膝关节内侧间室骨性关节炎患者共56例（56膝），所有手术均由同一资深骨科医师主刀。根据纳入标准，共纳入男16例，女40例；年龄50～82岁，平均（63.68±8.23）岁。患者体重指数21～30 kg/m2，平均（25.81±4.52）kg/m2。所有患者术前常规进行患肢负重正侧位、膝关节内外翻应力位、髌骨轴位X线片检查，以及膝关节MRI检查。

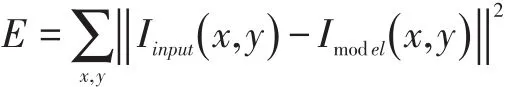
1.3 带表情的人脸重建

由于更普遍的图像中带有各种表情信息，因此为了重建出更加适合带各种有表情的人脸图像的三维模型，在形变模型的基础上加上表情模型，则可以延伸出新的形变模型。本文的形状模型来自Basel Face Model[2]（BFM）,表情模型来自Face Warehouse[3]。根据Chu等人[4]的研究结果，可以将原形变模型的形状模型改写成：

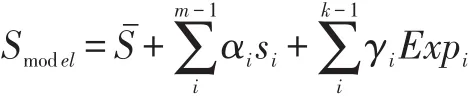
而对于三维纹理信息模型则保持不变，仍表示为：

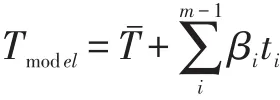
其中，k是表情模型中主元个数，m是形状模型和纹理模型主元个数，γ=(γ1,γ2,…γk-1)是表情系数，Exp=(Exp1,Exp2,…Expk-1)是表情主元向量组，α=(α1,α2,…αm-1)是 形状系数，s=（s1,s2,…sm-1）是形状主元向量组，β=（β1,β2,…βm-1）是纹理系数，t=（t1,t2,…tm-1）是纹理主元向量组。前面已经叙述了关于形变模型重建过程中通过纹理像素误差的平方和最小求解α，β系数，对于带表情的人脸重建过程，则只需要多求解一个γ系数即可。

在人脸表情领域中，二维特征点的位置能够很好的表现特定人脸图像的表情信息，为了求解表情系数，这里需要借助二维图片上的68个二维特征点，用二维特征点的位置信息来约束三维形状的三维特征点的二维投影，从而让三维形状产生一定的形变，通过这种三维特征点投影后与二维特征点的对应关系，如图1，我们可以估计出表情系数。这里我们预先把形状参数设置为0，则形状模型可以简化为：

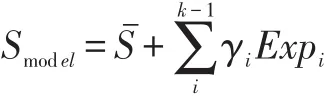
对于Smodel，我们可以找到68个三维特征点在二维投影上的68个二维坐标Uproj，为了让三维特征点在二维投影上的的位置跟输入图像的二维特征点U2d位置更接近，可以通过优化公式：

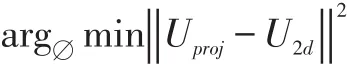
通过求解，这里能得到形状模型中的表情系数γ。

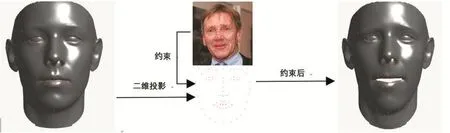
图1 通过二维特征点约束后的带表情的三维形状

2 实验结果

针对本文提出的添加表情模型的人脸重建方法，做了两组实验，一组是自然表情的三维人脸重建，另一组是带表情的人脸重建。实现结果表明，在形变模型基础上添加表情模型，能够对各种情况的人脸图片进行三维建模，这种建模方法体现出更好的通用性。本文用到的形变模型为BFM,表情模型为Face Ware⁃house。对于形变模型（BFM），经过预处理后的平均模型由53215个三维点，105840个三角面片组成，拉伸为向量时则表示成159645×1，形状主元向量s组则由159645×199组成，纹理主元向量组t由159645×199组成；对于表情模型，经过预处理后的表情主元向量组Exp由159645×29组成。

2.1 自然表情的人脸重建

如图2，左侧一列是选择自然表情的二维人脸照片作为输入，第二，第三列是三维重建的模型效果。

2.2 带表情的人脸重建

如图3，左侧一列是选择带表情的二维人脸照片作为输入，第二，第三列是三维重建的模型效果。

3 结语

本文主要初步探索了在添加人脸表情的情况下，基于形变模型的三维人脸重建。实验表明，不管是针对带表情的人脸图片，还是自然表情的图片，该方法可以达到预想的效果，这对于人脸重建更具有通用性和适用性。

重建精度是三维人脸重建的重要指标，怎样提高重建的精度是需进一步研究的方向；同时由于本文主要是针对正面照片做的重建工作，而对于侧面带表情的人脸重建工作还不够充分，因而这个方面也将成为后续的研究工作。

图2 自然表情的三维人脸重建

图3 带表情的三维人脸重建

参考文献：

[1]V.Blanz,T.Vetter.A Morphable Model for the Synthesis of 3D Faces.Proc.of SIGGRAPH'99，Los Angeles：1999.

[2]P.Paysan,R.Knothe,B.Amberg,S.Romdhani,T.Vetter.A 3D Face Model for Pose and Illumination Invariant Face Recognition.In Advanced Video and Signal Based Surveillance,2009.AVSS'09.Sixth IEEE International Conference on,pages 296-301.IEEE,2009.

[3]C.Cao,Y.Weng,S.Zhou,Y.Tong,K.Zhou.Face ware house:a3D Facial Expression Database for Visual Computing，2013.

[4]B.Chu,S.Romdhani,L.Chen.3D-Aided Face Recognition Robust to Expression and Pose Variations.In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition,pages 1899-1906,2014.

[5]龚勋，王国胤.基于特征点的三维人脸形变模型［J］.软件学报，2009，20（3）：724-733．

[6]胡永利，尹宝才，谷春亮，等．基于形变模型的三维人脸重建方法及其改［J］.计算机学报，2005，28（10）：1672-1678．