设施农业对农田排涝模数影响*
刘嘉男,李发文※,冯 平,王现领
(1.天津大学水利工程仿真与安全国家重点实验室,天津 300072; 2.天津市水利科学研究院,天津 300061)
0 引言
21世纪以来,全球发生洪涝灾害的频率高于过去[1]。随着全球环境的变化,这种趋势越加明显。研究表明, 较长时间尺度上,气候变化对水文水资源的影响更加明显,但是短期内,土地利用/覆被变化(LUCC)是水文水资源变化的主要驱动要素之一[2]。随着经济的发展,农业科学技术水平的提高,设施农业迅速发展,对农业产业结构调整和农民增收起到巨大作用。但是设施农业用地增加导致了不透水面积增大,使地表径流系数增大,进而导致农田区域产水量增大,对农田区域的排涝模数造成一定影响。而排涝模数对合理确定排涝系统规模、保障农田安全具有重要现实意义。因此,在设施农业得到快速发展的情况下,有必要开展设施农业对农田排涝模数影响的研究。
排涝模数的确定主要依赖于设计径流深,因此建立合理的降雨径流模型是进行排涝模数估算的基础。Stanford模型、Tank模型、Boughton模型、新安江模型、陆浑模型、SWAT模型等都是流域产流计算比较成熟的模型。产流模型主要应用于大尺度流域,对山区模拟效果较好,而对平原区产流模拟精度一般较差。平原区产流机制更为复杂,下垫面多样且变化,超渗产流与蓄满产流模式并存,采用单一产流模型时,往往不能更全面、更真实地反映平原区的产流机制,导致模型精度达不到使用要求。文章选用包为民[3]提出的超渗—蓄满垂向耦合产流模型,该模型很好地解决了平原区超渗与蓄满产流模式并存问题,在平原区得到了广泛应用[4]。考虑到农田区域实测径流资料往往需要反演推算,资料的准确度不高,而农田可以获得实测土壤含水量和地下水位资料,因此在模型合理性评价中,除了采用实测径流相对误差作为模型的评价标准外,还采用实测土壤含水量以及实测地下水位的效率系数和相对误差作为模型的评价标准,以有效提高模型模拟的精度。
模型参数敏感性分析和参数优化对模型模拟结果有重要影响[5-6]。该文选用最具代表性的全局参数敏感性分析方法Sobol′法[7],该方法已经广泛应用于众多水文模型参数敏感性分析中[8-10]。在模型参数优化选择中,SCE-UA算法也得到了广泛应用[11],王维[4]首次将SCE-UA用于垂向耦合模型中,并与新安江模型进行对比,证明了SCE-UA算法在两种模型中的有效性。
该文选择具有一定设施农业规模的封闭小区为研究区,构建超渗—蓄满垂向耦合模型,基于Latin超立方抽样,进行Sobol′全局敏感性分析以及SCE-UA全局参数优化,同时考虑土壤含水量与地下水位变化量,与人工率定相结合,进行模型参数的优选。针对不同重现期的设计暴雨,通过已经构建好的模型求得农田小区的产流量,用平均排除法计算不同重现期下的设计排涝模数,与2003年《天津市平原地区农田除涝水文手册》(简称《除涝手册》)进行对比,探讨设施农业下对原除涝手册修订的必要性。

图1 研究区概况及站点布设
1 材料与方法
1.1 数据获取与处理
研究区域位于天津市西青区张家窝镇,属于半湿润半干旱区。建立产流模型所需要的数据均为现场试验实测资料,在试验区内设置雨量计、土壤墒情测量仪、地下水位观测仪、泵站排水流量计等观测设备,可得到降雨量、土壤含水量、地下水位变化量以及泵站排水量数据系列,为模型建立提供了可靠的数据来源。设备具体型号为:自动雨量计:LC-YL1、土壤水分传感器:FDS120、超声波流量计:SCL-80、压阻式水位计:Unisens-WL20。研究区域概况及站点布设见图1。
通过2016~2017年的现场试验,采集到8场降雨过程。对观测的降雨量、土壤含水量、地下水位相对变化量、泵站排水量数据以1h为计算时段进行整理,并将土壤含水量与地下水位相对变化量转化为水层深度(mm),方便建模使用。
经调研,该农田小区在2008年之前全部为经济林木,随着天津“菜篮子”工程的实施,设施农业迅猛发展[12],占地面积为3.709 8万m2, 占总面积的7%; 2011年底,设施农业占地面积进一步扩大,占地面积为7.753 1万m2,占总面积的15%; 2012年底至今,设施农业面积所占比例达到41%,研究区域设施农业发展概况见图2。

图2 研究区域设施农业发展概况
1.2 超渗—蓄满耦合产流模型建立
1.2.1 透水面(农田)

降雨P扣除蒸散发E后的净雨量PE到达地面,首先通过空间分布的下渗曲线,判断是否发生超渗产流,当发生超渗产流时,采用具有流域分布特征的格林—安普特下渗曲线计算超渗产流量和下渗量[13],然后以超渗产流的下渗量作为蓄满产流中的降雨输入量。在土壤缺水量大的面积上,补充土壤含水量不产流,在缺水量小的面积上,补足土壤缺水量后,发生蓄满产流[3]。
超渗产流量计算过程为[3]:
PE=P-E-I
(1)
(2)
FMM=FM×(1+B1)
(3)
(4)
R1=PE-FA
(5)
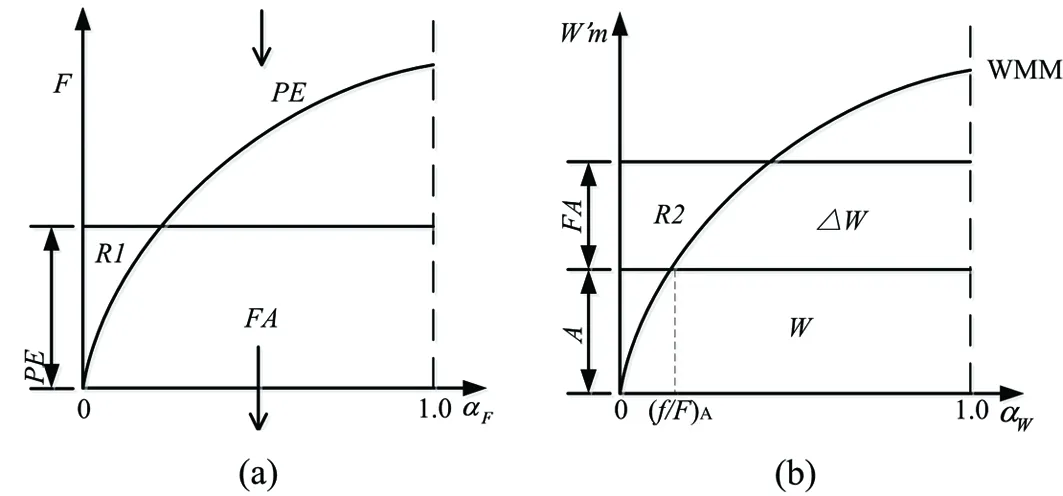
图3 模型垂向耦合形式
其中,P为降雨量,mm;E为蒸散发量,mm;I为植物截留量,mm;PE为净雨量,mm;FM为农田小区平均下渗能力,mm/h;FC1为稳定下渗率,mm/h;K2为土壤缺水量对下渗率影响的灵敏度系数;FMM为平均下渗率为FM时上层最大点的下渗率,mm/h;FA为实际下渗量,mm;WM为土壤平均蓄水容量,mm;W为土壤含水量,mm;B1为下渗能力分配曲线的指数,反映了下渗能力分布的不均匀性;R1为超渗产流量,mm。
地面以下的径流,采用蓄满产流结构,计算公式为:
(6)
WMM=WM×(1+B2)
(7)
(8)
式中,A1为前期影响雨量,mm;WMM为土壤内最大点蓄水容量,mm;B2为蓄水容量—面积分配曲线的指数,反映了蓄水容量分布的不均匀性;R2为蓄满产流量,mm; 式中其他符号含义同前。
总产流量R为超渗产流量R1与蓄满产流量R2之和,即:
R=R1+R2
(9)
蓄满产流计算出的产流量R2包括地面径流R2S和地下径流R2G两部分,可以用稳定下渗率进一步划分。计算过程为:
(10)
其中,FC2为下层土壤稳定下渗能力,mm/h。
蒸散发量与土壤含水量的计算采用新安江模型中描述的三层蒸散发模式[14],植物截留量对1次降雨径流过程的影响量很小,但对年降水量而言,森林及茂密的植被,1年中截留的水量可达年降水量的25%~30%,这些截留的水量最终消耗于蒸散发,因此该文中将植物的截留作用合并于降雨的蒸散发损失中。这样就构成了完整的超渗—蓄满垂向耦合产流模型。
1.2.2 不透水面(设施农业)
在不透水面积上的产流量为直接径流DRS,其计算式为:
DRS=P×IMP×α0
(11)
α0=0.95,RS>0
(12)
其中,IMP为不透水面所占面积比例,经测量取值为0.41;α0为不透水面产流系数;RS为透水面地面总径流,即R1与R2S之和。
1.2.3 总产流计算
透水面积与不透水面积上的产流一起汇入河道,经泵站排出,泵站出水口处产流深计算公式为:
R总=(1-IMP)×R+α0×IMP×P
(13)
其中,R总为区域内总径流模拟值,mm。
综上所述,在研究区域透水面上采用超渗—蓄满垂向耦合结构,地面径流R1按超渗产流计算,地面以下径流按蓄满产流计算,并依据下层土壤下渗能力分为地面径流R2S和地下径流R2G,其中,R1与R2S以及不透水面上的产流量DRS汇入河道,经泵站排出。蓄满产流中的地下径流R2G补充地下水位。超渗—蓄满垂向耦合模型流程图见图4。

图4 超渗—蓄满耦合产流模型流程图
1.3 模型参数敏感性分析及率定
通过Latin超立方抽样随机生成符合要求的参数组,选用Sobol′敏感度分析方法进行全局参数的一阶敏感度与总敏感度计算,采用SCE-UA算法进行全局参数自动率定,同时结合敏感性分析的成果与模型适用性评价标准进行人工率定,最终得到模型的参数。
1.3.1 Latin超立方抽样
Latin超立方抽样作为Monte-Carlo方法的改进,提供了1个有效而实用的小样本采样技术,在具有随机输入变量的复杂模型分析中应用广泛。该抽样方法的本质是将N维单位立方体中的每一维坐标区间[0, 1]等分成n个等间距不重叠的子区间,对每个子区间分别进行独立的等概率抽样,这样每个样本点都属于特定的分层区间,然后将抽到的每一分量进行随机组合,从而可以使样本点更均匀地分布在参数的可行域内,通过较少的采样得到相同的效果[15],根据Tang等[16]的研究成果,选用Latin超立方技术对参数进行抽样,实现对模型参数的全局敏感性分析以及参数优化。
1.3.2 Sobol′全局敏感度分析法
Sobol′方法是一种基于方差分解的全局模型敏感度分析方法,可以用于非线性和非单调函数和模型[17],该方法的核心是将所研究的模型分解为单参数及多参数相互组合的函数,分别求出每项对应于模型输出的敏感度系数。假设产流模型为Y=f(X),X=(x1,x2,…,xm),其中,Y为模型输出的目标函数,X=(x1,x2,…,xm)为影响产流模型的m个待分析参数,X服从[0, 1]上的均匀分布,且f2(x)可积,定义Θm为模型输入参数的空间域,表示为Θm=(X|0≤xi≤1,i=1, 2,…,m),将模型分解为2m项之和[18]:
(14)
其中,f0为常数项,保证模型分解的形式具有唯一性,要求其余子项对其所包含的变量的积分为0,即满足公式:
(15)
则Y的方差D(Y)可以作分解:
(16)
其中,Di为参数ii产生的方差;Dij为两个参数和j相互作用产生的方差;Dijk为3个参数ijk相互作用产生的方差;D12…m为m个参数共同作用产生的方差。将式(16)归一化后得到各参数和参数相互作用的敏感性:
(17)
产流模型参数i对目标函数的敏感度值可表示为:
(18)
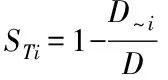
(19)
其中,一阶敏感度Si为参数i作用的敏感度; 总敏感度STi为参数i单独作用以及与其他参数相互作用的敏感度;D~i为除了参数i之外的参数的方差。
由于水文模型具有很大的非线性和复杂性,运用Sobol′法进行敏感度计算时,对产流模型中待分析的变量进行两次独立抽样,得到ON×m和PN×m两个矩阵,其中,N为抽样次数,m为参数个数,即:
(20)
(21)
(22)
(23)
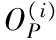
1.3.3 SCE-UA算法
SCE-UA(Shuffled Complex Evolution Algorithm)算法是由美国亚利桑那州大学Duan等[11]于1992年提出来的,其综合了随机搜索算法、单纯形法、聚类分析法及生物竞争演化等方法的优点,收敛速度较快、鲁棒性强、稳定性好,可以高效解决高维非线性参数的全局优化问题,且不需要显式的目标函数或者目标函数的偏导数。该算法的详细步骤如图5。

图5 SCE-UA算法流程图
1.4 模型适用性评价
产流计算的准确率与可信度是进行排涝模数计算的保障,根据《水文情报预报规范》(SD 138-85)[19],水量平衡评价指标选取径流深相对误差,地下水位变化量与土壤含水量变化量选取相对误差Re和Nash效率系数Ens评价模型模拟精度。计算公式为:
(24)
(25)
为了进一步验证上述产流计算模型,分别采用单一的超渗产流模型、蓄满产流模型以及该文中建立的超渗—蓄满垂向耦合模型计算,计算模型相对有效性[3]。计算公式:
(26)
(27)
其中,CEFc代表耦合产流相对于超渗产流的有效性;CEFx代表耦合产流相对于蓄满产流的有效性;R0为实测降雨径流深,mm;Rc、Rx、RH分别为用超渗、蓄满和耦合模型计算的降雨径流深,mm。
1.5 排涝模数计算
采用平均排除法计算排涝模数,即将相应不同重现期下的降雨产流量在规定的排涝天数内均匀排除[20]。该方法概念明确、所需资料较少,计算方便。计算公式为:
(28)
其中,M为设计排涝模数,m3/(s·km2);R为设计径流深,mm;td为排涝天数,d。天津市的排涝标准为1日暴雨2日排除[21],即td=2。
表1 超渗—蓄满垂向耦合模型参数含义及取值范围

序号参数参数含义上限下限1K1陆面蒸散发能力折算系数050952C深层蒸散发系数01023FC1上层稳定下渗率4654K2土壤缺水量灵敏度系数15355WUM上层土壤蓄水容量20506WLM下层土壤蓄水容量40707WDM深层土壤蓄水容量65908B1土壤下渗能力分配曲线指数03089B2蓄水容量—面积分配曲线指数020610FC2下层土壤稳定下渗率254
2 实例应用
2.1 研究区域水文模型构建
按照1.2所述过程构建了该农田小区超渗—蓄满垂向耦合模型,模型共有10个参数。利用两年现场试验所经历的8场降雨事件,进行模型参数的敏感性分析以及参数率定与验证,以得到优选的模型参数。
2.2 基于Sobol′的参数敏感性分析
因为没有关于参数的先验信息,进行敏感性分析输入的参数值是从均匀分布中抽取的,不同的参数范围在0~1之间进行线性变换[22]。产流模型中参数的取值上下限见表1。利用Latin超立方抽样,在参数的取值范围内随机生成包含2 000组参数的两个样本[3, 14, 23]。
模型参数的敏感性与目标函数相关联,该文选取径流深与径流深相对误差两个指标作为目标函数。根据雨量等级将率定期5作为目标函数。根据雨量等级将率定期5场降雨进行划分,最终选取3场降雨(其中160720场次降雨221.8mm,为特大暴雨; 160807场次降雨92mm,为暴雨; 160724场次降雨41.2mm,为大雨)进行各参数一阶敏感度与总敏感度的分析。
3种典型降雨下10个参数对2个目标函数的一阶敏感度与总敏感度值分布情况见图6。每一列代表同一目标函数下模型参数在3种典型降雨中的表现。该文中指定总敏感度超过阈值10%(图6中虚线)的参数为敏感参数。
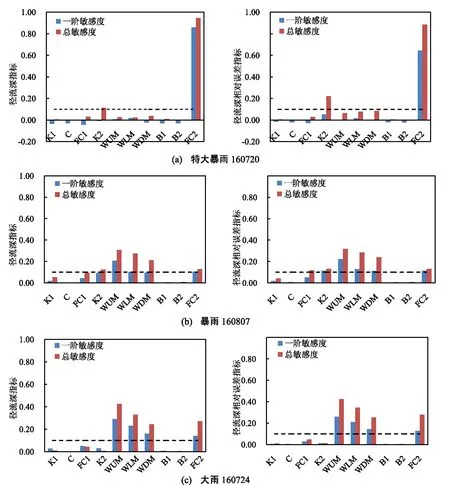
图6 3种典型降雨下10个参数对不同目标函数的一阶敏感度与总敏感度图注:每幅图中的左边图柱为一阶敏感度;右边图柱为总敏感度
通过分析图6,发现当以径流深和径流深相对误差为评价指标时,参数在相同等级的降雨中所呈现的规律是一致的。在特大暴雨时,一阶敏感度最大的参数是FC2,较敏感的参数是FC1,总敏感度最大的是FC2,其次为K2; 在暴雨中,一阶敏感度与总敏感度最大的参数均是WUM,WLM、WDM、FC2、K2、FC1均为敏感参数,K1为较敏感参数; 在大雨中,一阶敏感度与总敏感度最大的参数依然均是WUM,WLM、WDM、FC2,FC1为敏感参数。
2.3 基于SCE-UA的自动率定
在进行参数优化时,将率定期5场降雨综合考虑,以径流深相对误差为核心,采用表2目标函数,通过SCE-UA算法,自动寻找到使目标函数值达到最小,且满足单场次降雨径流深相对误差在20%范围内的最优参数组。
SCE-UA算法自身包含多个参数,根据前人研究成果[11, 24],该文中算法参数取值见表3,参数优化的可行域与表1相同。
表2 SCE-UA算法目标函数

评价目标目标函数平均相对误差MAPEMAPE=1N∑Ni=1Ri,obs-Ri,simRi,obs最大相对误差MMPEMMPE=maxRi,obs-Ri,simRi,obs()平均相对对数绝对误差MLGMLG=1N∑ni=1logRi,obs-Ri,simRi,obs+1[]总目标函数Fmin(F)=∑MLG+MAPE+MMPE() 注:表2中,Ri,obs为场次降雨i的实际径流深,Ri,sim是场次降雨i的模拟径流深;i=1,2,…,N;N为场次降雨总数
表3 SCE-UA算法参数设置

参数名称参数意义参数取值n待优化参数的个数10p复合形个数2m每个复合形的顶点数21s样本点数42q每个子复合形的顶点数11α父代产生子代的个数1β父代产生子代的代数21T最大循环次数100/200/1000/2000
通过Latin超立方抽取42组参数,以表2总目标函数对率定期5场降雨综合考虑,最大迭代次数T分别设置为100/200/1 000/2 000,并分别连续运行5次,初步率定出一组较优参数,结果见表4。此时,总目标函数值以及单场次径流深相对误差值见表5。各场次径流深相对误差均在20%内,满足要求。
表4 参数初步率定结果

参数K1CFC1K2WUMWLMWDMB1B2FC2参数值055013643307453568417801031021254

表5 目标函数值及单场次径流深相对误差

表6 参数率定结果
2.4 自动率定与人工率定相结合
在SCE-UA参数优选过程中,蒸散发计算与两水源划分参数,即K1、C、WUM、WLM、FC2波动比较大; 产流计算参数FC1、WDM相对比较收敛; 产流计算参数K2、B1、B2较稳定。其中K1、C、B1、B2为不敏感参数,在率定过程中,可以对K1取多次寻优结果的平均值0.75; C根据经验可以取0.17; B1、B2取自动率定结果值,分别为0.3和0.2。其他敏感参数的率定还需要结合产流区域实际情况进一步分析。
鉴于产流区域实测降雨场次较少,没有实测流量过程线,缺少对产流过程的模拟,因此在参数率定过程中,不仅以径流深相对误差为评价指标,还需考虑地下水位变化与土壤含水量变化过程,提高模型的模拟精度。地下水位主要受地下径流的影响,着重调节FC1与FC2使地下水位变化过程满足要求; K2、WUM、WLM、WDM与土壤含水量有密切关系,调节这4个参数使土壤含水量评价指标满足要求。自动率定与人工率定结合得到的参数数值见表6。
2.5 模型适用性评价
按照1.4计算式(24)(25)计算,率定期与验证期各项评价指标结果见表7,按照式(26)(27)选取8场降雨计算垂向耦合模型相较于单一超渗模型和单一蓄满模型的有效性,结果见表8。
表7 模型评价指标分析

模拟期降雨场次评价对象Nash系数相对误差(%)率定期160720地下水位变化量0671564土壤含水量079491径流深相对误差(%)512160724地下水位变化量0741257土壤含水量061561径流深相对误差(%)562160801地下水位变化量0681437土壤含水量074605径流深相对误差(%)254160807地下水位变化量0781324土壤含水量080811径流深相对误差(%)1210160818地下水位变化量0751263土壤含水量073417径流深相对误差(%)1067验证期170706地下水位变化量0721058土壤含水量081763径流深相对误差(%)271170709地下水位变化量0681239土壤含水量071834径流深相对误差(%)1593170722地下水位变化量0801161土壤含水量087637径流深相对误差(%)510
表8 产流结果计算成果

降雨场次降雨量(mm)实测流量(m3)R0(mm)RC(mm)R0⁃RCR0(%)RX(mm)R0⁃RXR0(%)RH(mm)R0⁃RHR0(%)1607202218962561899815438187423320-2275178905831607243823380667635479746-117963055516080141248809639610271199-2451940239160807922850056256323-1240501810796305-120916081835232806475641288732-1305578106617070649449809831016-3371333-35621010-27617070933448609591140-18851316-37201112-159317072247849609799433671305-3331929510汇总CEFc=0869CEFx=0912
由表7可知,率定期与验证期地下水变化量与土壤含水量变化量的Nash效率系数均大于0.6,各项相对误差均控制在20%之内,可以认为模型是合理的。
由表8可知,垂向耦合模型相对于超渗产流的有效性为0.869,相对于蓄满产流的有效性为0.912,进一步证明了在该农田小区采用超渗蓄满垂向耦合产流模型是合理的。
2.6 排涝模数计算
2.6.1 降雨趋势分析
利用5年滑动平均值对1990~2015年年降雨量及汛期(6~9月)降雨量进行趋势分析[25],结果见图7。

图7 降雨趋势分析
通过图7(a)与(b)发现,1990~2015年,年降雨量以及汛期降雨量波动平稳,没有显著线性变化趋势。因此,分析设施农业对农田排涝模数影响时,可以不考虑降雨变化对其影响。
2.6.2 设计暴雨计算
采用2015年《天津市暴雨图集》24h暴雨参数等值线图,得研究区域中心年最大24h暴雨量均值为98.8mm,变差系数CV为0.45,采用CS=3.5CV。查P-Ⅲ型曲线KP表,即可算出研究区域不同重现期24h设计点雨量,因研究区域面积仅50.70万m2,点面折算系数为1,故用设计点雨量代表面雨量计算,不同重现期24h设计面雨量成果见表9。
表9 不同标准24h设计面雨量成果

重现期3年5年10年20年Kp10813116018824h设计点雨量(mm)1066112900157941859224h设计面雨量(mm)10661129001579418592

表10 不同重现期下设计径流深与排涝模数对比
2.6.3 排涝模数计算
根据研究区附近天津耳闸站24h设计暴雨的时程分配,将不同重现期设计面雨量进行分配,代入超渗蓄满垂向产流模型中,计算不同重现期下的设计径流深,代公式(28)求得相应的排涝模数,与2003年《除涝手册》中给出的设计排涝模数进行对比,结果见表10。
由表10可知,不同重现期下的设计径流深和排涝模数与原手册设计排涝模数相比发生了较大变化,与原设计排涝模数相比均有所增加,增大的幅度在16.44%~3.77%之间,且变化幅度随重现期增大而减小。由降雨趋势分析可知,基准期与评价期的降雨没有发生变化,因此设计排涝模数变化,主要是由于设施农业占比增加造成的。
3 结论
(1)通过开展农田小区现场试验,布设水文要素测量站点,减小了模型输入数据的误差,同时考虑了地下水位与土壤含水量的变化,提高了模型的模拟精度。与单一超渗模型和蓄满模型进行对比,有效性分别提高了0.869和0.912,验证了在该农田小区建立的超渗—蓄满垂向耦合模型的有效性。
(2)在SCE-UA全局参数优化中结合Sobol′全局敏感性分析的成果,综合考虑模型结构,充分利用实测资料,高效优化了模型参数,各项评价指标的Nsah系数均高于0.6,相对误差在20%以内。
(3)随着农业现代化进程的加快,试验农田小区中设施农业所占比例逐年提高,对水文要素和产流过程有较大影响, 3年、5年、10年、20年一遇重现期下的设计排涝模数与原《除涝手册》相比,分别增加16.44%、8.63%、7.50%、3.77%。通过降雨趋势分析,基准期与评价期的降雨没有显著线性变化趋势,因此设计排涝模数的变化主要是由于设施农业占比增加引起。由此可以看出设施农业对设计排涝模数的影响较大,这为天津市近郊区设施农业下农田设计排涝模数的修订提供了有效依据,对合理确定排涝系统规模、有效控制涝灾、保障农业安全生产具有重要的现实意义。
[1] Mwangi H M, Julich S,Patil S D,et al.Modelling the impact of agroforestry on hydrology of Mara River Basin in East Africa.Hydrological Processes, 2016, 30(18): 3139~3155
[2] 胡华浪, 李伟方,易湘生,等.土地利用/覆盖变化对永定河流域水文过程的可能影响模拟.中国农业资源与区划, 2016, 37(3): 74~83
[3] 包为民, 王从良.垂向混合产流模型及应用.水文, 1997,(3): 18~21
[4] 王维, 冯忠伦,杨伟,等.基于SCE-UA算法的新安江模型与垂向混合产流模型参数优化应用研究.中国农村水利水电, 2017,(3): 26~30
[5] Song X, Zhang J,Zhan C,et al.Global sensitivity analysis in hydrological modeling:Review of concepts,methods,theoretical framework,and applications.Journal of Hydrology, 2015, 523(523): 739~757
[6] 宋晓猛, 张建云,占车生,等.水文模型参数敏感性分析方法评述.水利水电科技进展, 2015, 35(6): 105~112
[7] Sobol I M. Sensitivity analysis for non-linear mathematical models.Mathematical Modeling & Computational Experiment, 1993, 1: 407~414
[8] 齐伟, 张弛,初京刚,等.Sobol′方法分析TOPMODEL水文模型参数敏感性.水文, 2014, 34(2): 49~54
[9] Zhang C, Chu J,Fu G.Sobol′s sensitivity analysis for a distributed hydrological model of Yichun River Basin,China.Journal of Hydrology, 2013, 480:58~68
[10]张小丽, 彭勇,徐炜,等.基于 Sobol′ 方法的新安江模型参数敏感性分析.南水北调与水利科技, 2014,(2): 20~24
[11]Duan Q Y, Gupta V K,Sorooshian S.Shuffled complex evolution approach for effective and efficient global minimization.Plenum Press. 1993
[12]黄学群, 李瑾,宋建辉,等.天津现代农业园区发展模式与对策研究.中国农业资源与区划, 2012, 33(6): 79~84
[13]包为民. 格林—安普特下渗曲线的改进和应用.人民黄河, 1993,(9): 1~3
[14]赵人俊. 流域水文模拟.北京:中国水利电力出版社,1984
[15]方磊. 基于LHS抽样的不确定性分析方法在概率安全评价中的应用研究.合肥:中国科学技术大学, 2015
[16]Tang Y, Reed P,Wagener T,et al.Comparing sensitivity analysis methods to advance lumped watershed model identification and evaluation.Hydrology & Earth System Sciences, 2007, 3(6): 793~817
[17]Sobol I M. On sensitivity estimation for nonlinear mathematical models.Keldysh Applied Mathematics Institute, 1990, 2(1): 112~118
[18]Sobol I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates.Mathematics & Computers in Simulation, 2001, 55(1-3): 271~280
[19]中华人民共和国水利部. 水文情报预报规范SD 138-85.北京:中国标准出版社,2008
[20]于畅, 郝曼秋,高成,等.平原城市自排区排涝模数计算方法研究.水资源与水工程学报, 2014,(6): 184~186
[21]水利部. 灌溉排水工程设计规范GB50288-99.北京:中国计划出版社,1999
[22]Nossent J, Elsen P,Bauwens W.Sobol′ sensitivity analysis of a complex environmental model.Elsevier Science Publishers B.V.2011, 26(12): 1515~1525
[23]李发文, 冯平,张超.天津北三河地区垂向耦合产流模型及应用.吉林大学学报(地), 2011, 41(2): 459~464
[24]马海波, 董增川,张文明,等.SCE-UA算法在TOPMODEL参数优化中的应用.河海大学学报(自然科学版), 2006, 34(4): 361~365
[25]傅宁, 史珺,任雨.1951~2012年天津地区汛期降水变化特征分析.干旱区资源与环境, 2014, 28(4): 83~88

