基于高速图像采集的全角度跌落控制方法研究

王 睿，郭阳宽，郭会梁，孙文艺

(1.北京信息科技大学光电测试技术北京市重点实验室，北京 100192；2.北京沃华慧通测控技术有限公司，北京 100085)

0 引言

随着智能手机及平板计算机等消费类触屏数码产品的大范围普及，大尺寸触屏的跌落抗损性已成为大众选择产品时需要考虑的因素之一。另外，产品内部功能模块的布局合理性也会影响其跌落抗损性。以智能手机为例，手机生产厂家必须进行跌落试验，实现对手机质量及设计的合理性评估。

手机跌落测试主要包括两个方面：跌落高度和手机触地角度。目前，国内外对手机的跌落测试只能实现特定高度的跌落，无法实现准确的触地角度控制。为了降低实际跌落试验的成本，研究人员采用有限元仿真方法，对手机跌落试验进行分析。韩克明利用Abaqus/Explicit对手机跌落进行有限元分析，验证跌落式整机触摸屏玻璃的可靠性[1-2]；彭必友将计算机仿真技术应用于整机自由跌落试验中[3]；祖景平利用有限元软件PATRAN/DYTRAN软件，对手机跌落模拟进行仿真[4]；李鹏忠通过CAE方法，对自由跌落试验进行仿真[5]。

针对跌落高度及触地角度的控制问题，本文利用电机对手机触地的瞬间速度进行控制，从而实现对不同跌落高度的模拟；同时，利用两个正交分布的电机，实现对触地角度的精确控制。

1 手机跌落模型

手机跌落试验主要实现对跌落过程中产生的屏幕、摄像头、按键等可能性损伤进行模拟测试。为了便于直观地了解手机触地位置，手机各部位定义如图1所示。

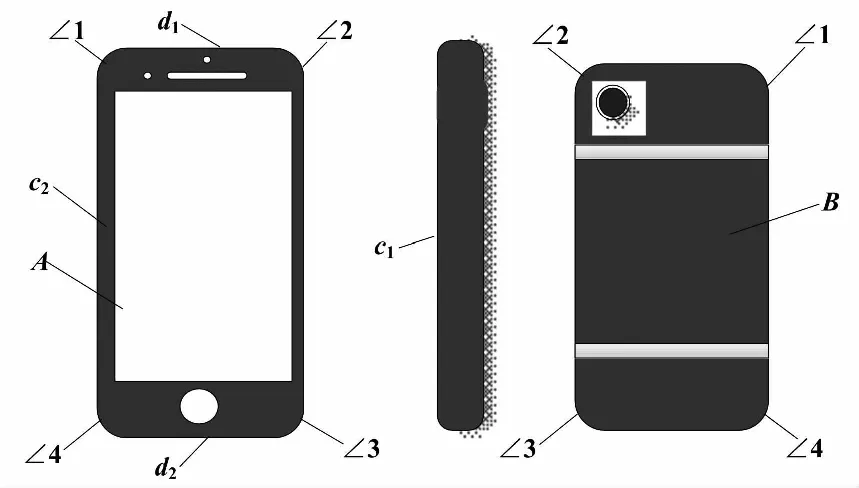
图1 手机各部位定义图 Fig.1 Definition of each part of the mobile phone

图1中：∠1、∠2、∠3和∠4分别为手机的4个角；A、B分别为手机的正、反面；c1、c2为带有按键的两个侧面；d1、d2分别为顶端和底端侧面。

手机的主屏幕材质为铝硅酸盐玻璃，无论是正面落地或者某个角落地，主屏都是容易损伤且容易观察的部分。当手机跌落过程中与地面接触的部位是∠2，除了手机屏幕出现损伤之外，手机摄像头也可能出现损伤。c1、c2面落地时，会给手机侧面按键造成巨大的损伤。

为了对手机跌落瞬间的速度及触地角度进行定量分析，并据此对整机设计合理性进行评估。本文分别对跌落高度及触地角度进行建模分析。

1.1 跌落高度模型

实际使用过程中，手机跌落可认为是自由落体运动，已知自由落体运动公式为：

(1)

式中：v为落地瞬间速度；g为重力加速度；t为自由落体运动时间；H为跌落初始位置距离地面高度。

为了对不同跌落高度的手机跌落过程进行模拟，本文利用加速电机对手机竖直方向的速度进行控制，并在运行一定加速时间后使手机进行自由落体运动，从而实现超过跌落仪竖直高度的跌落试验。手机落地瞬间速度为：

v1=at1+gt2

(2)

(3)

式中：a为加速电机加速度；t1为电机加速时间；t2为自由落体时间。

1.2 触地角度模型

利用正交旋转的两个电机改变手机初始角度。以图1中的∠4为原点、d2边为x轴、c2边为y轴，建立空间直角坐标系，对步进电机控制角度进行说明。手机在水平、竖直两个方向进行旋转。触地角度旋转方式如图2所示。

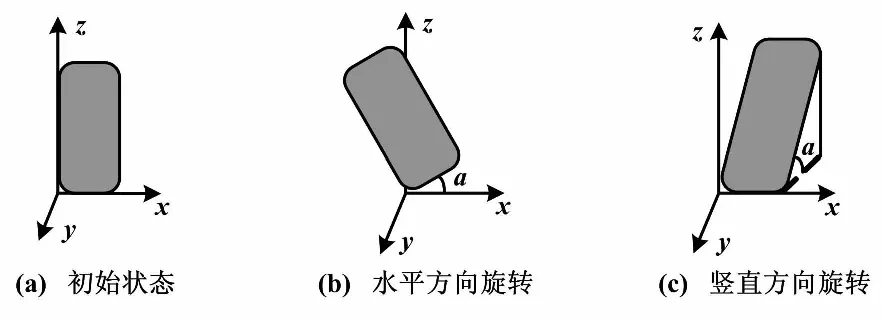
图2 触地角度旋转方式示意图 Fig.2 Angular rotation mode of touch ground

2 试验及结果分析

2.1 硬件系统搭建

本系统的加速电机采用42BHH39-152A-27C，最高转速为15 160 r/min。改变手机水平、竖直方向初始角度的两个旋转电机型号为DT42HS40-0903，步距角为1.8°。为了提高控制精度，选择的编码器型号为HKT2204-702C1-256B-5E，编码器的分辨率为0.029°。利用UX100高速相机对手机触地瞬间进行高速图像采集，高速相机分辨率为(1 280×1 024)pixels，每个像素点尺寸为(10×10)μm，采样频率为204 800帧/s，采样间隔为3.9 μs。

2.2 跌落速度分析

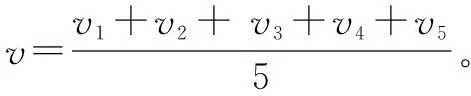
通过改变下落加速度的大小，模拟不同高度的跌落试验。跌落试验下落高度为1 m。由自由落体定律可知，在落地高度不变的情况下，落地瞬间速度仅与加速度有关，故可以根据落地瞬间速度来计算加速度：

(4)

a=gh

(5)

式中：vt为模拟的落地瞬间速度；h为模拟的高度。

在不改变下落高度的情况下，可以通过改变加速度的大小来模拟不同高度的自由落体运动。不同跌落高度对应的落地瞬间速度如表1所示。

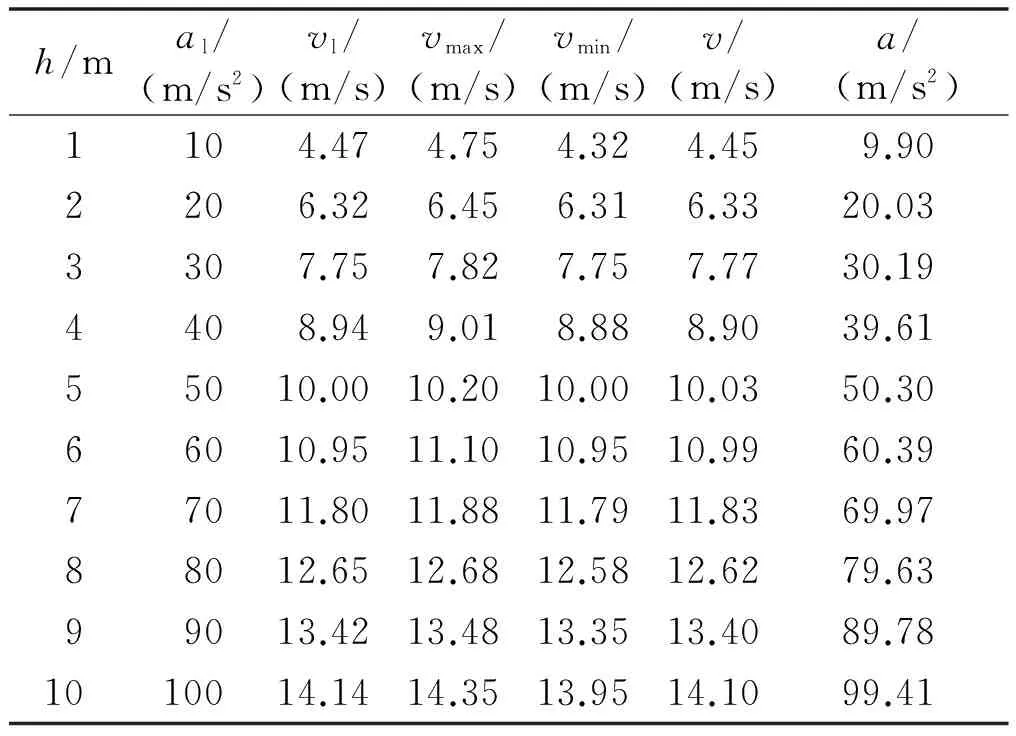
表1 不同跌落高度对应的落地瞬间速度Tab.1 Different drop height corresponds to theinstant speed of landing

表1中：al为模拟的理论加速度；vl为模拟的落地瞬间速度；vmax为20次跌落试验最大速度；vmin为20次跌落试验最小速度；v为跌落试验平均速度；a为跌落试验真实加速度。

通过比较加速度a与理论加速度al可以看出，本系统的误差值在5%之内。

2.3 跌落角度分析

手机跌落初始角度可以通过控制步进电机进行控制，手机落地瞬间角度则需要通过坐标变换得到。由于世界坐标系和摄像机坐标都是右手坐标系，所以其不会发生形变。若想将世界坐标系下的坐标转换到摄像机坐标下的坐标，可以采用刚体变换的方式。空间坐标系之间可以通过坐标变换进行相互转换：

(6)

XC=RX+T

(7)

式中：XC为摄像机坐标系；X为世界坐标系；R为旋转矩阵；T为平移矩阵。R、T与摄像机无关，受x、y、z三个方向上的分量共同控制，所以其具有三个自由度。R为分别绕X、Y、Z三轴旋转的结果。

摄像机绕X轴旋转后得到的坐标为r1，坐标变换为：

(8)

摄像机绕Y轴旋转后得到的坐标为r2，坐标变换为：

(9)

摄像机绕Z轴旋转后得到的坐标为r3，坐标变换为：

(10)

R=r1×r2×r3。摄像机由三个方向的θ控制，故具有三个自由度。

采用中心投影法将需要进行坐标变换的物体投射到投影面上，从而获得一种较为接近视觉效果的单面投影图，如图3所示。

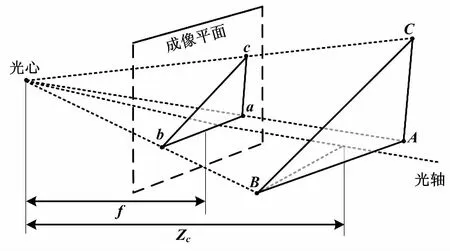
图3 单面投影图 Fig.3 Single-side chart

以图3中B(XB,YB)点为例，在小孔成像摄像机模型下，可以利用简单的相似三角形比例关系，求出成像平面上的投影点b(xb,yb)的坐标：

(11)

式中：f为摄像机的焦距。

式(11)阐明了摄像机坐标与图像坐标之间的透视投影关系。将三者相乘，写成一个矩阵P：

(12)

式中：P为世界坐标到图像坐标的转换矩阵。通过坐标变换求出手机落地瞬间的角度，并根据手机落地后损坏程度，得出手机落地角度跌落对手机损坏程度的影响。

由试验结果可知，∠4首先与跌落面接触。设∠4与跌落面接触点为p点，d1边中点设为q点，以一个像素间隔为一个单位，利用坐标平移矩阵将p点平移至坐标原点，平移向量T= [-30，-40,0]-1，则p点坐标为(0,0,0)，q点坐标为(5,10,4)。向量pq=[5,10,4]，将向量pq分别投影到xoy,yoz和xoz平面，得到的向量分别为pqxoy=[5,10],pqyoz=[10,4]和pqxoz=[5,4]。跌落角度旋转方式如图4所示。

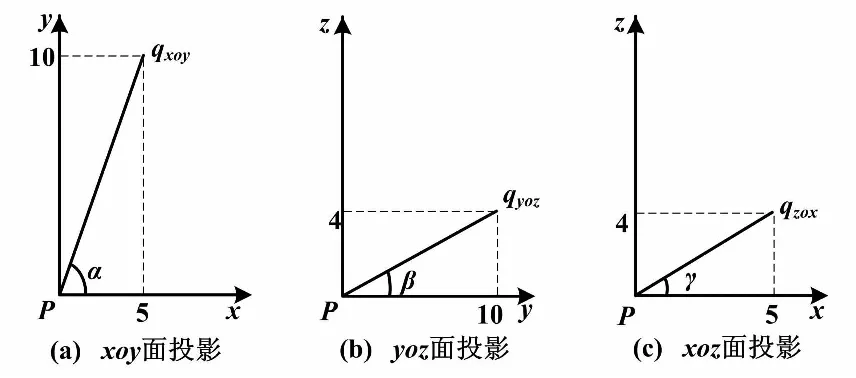
图4 跌落角度旋转方式示意图 Fig.4 Angular rotation mode of falling

图4中：α、β、γ可以用三角形变换关系得到。其中：α=63.43°,β= 21.80°,γ= 38.66°。根据立体几何关系，可得手机落地瞬间立体角θ1= 60.91°。通过20次重复试验，可以得出手机落地瞬间最大立体角θmax=65.32°，手机落地瞬间最小立体角θmin=57.58°。通过数据处理可以得出手机跌落瞬间立体角平均值θmax=65.32°。同理可得当初始角度为30°、45°时的计算结果。不同跌落角度对应落地瞬间角度如表2所示。

本系统通过电机控制改变手机跌落初始角度的大小，根据落地瞬间角度的差异以及手机损坏程度，分析跌落角度对手机损坏程度的影响。

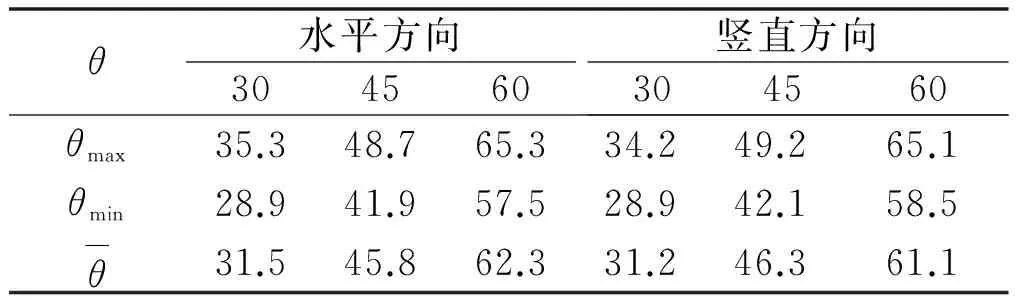
表2 不同跌落角度对应落地瞬间角度Tab.2 Different drop angles correspond to themoment Angle of landing (°)

3 结束语

本文通过改变跌落的加速度的大小[6-12]，模拟不同的跌落高度进行试验，分析落地速度对试验结果的影响；改变手机初始角度的不同，分析跌落角度对试验结果的影响。本文设计的跌落仪，可以实现对手机跌落的全方位测试，能够模拟高度1.0～10.0 m之间的跌落，并且手机跌落的初始角度可以在180°的范围内自由变换。大量试验证明，本系统具有良好的可靠性、稳定性，能够满足手机出厂前的跌落试验要求。

参考文献:

[1] 韩克明,孙志刚,林墨洲.手机触摸屏抗跌落仿真分析[J].计算机辅助工程,2013(S2):418-420.

[2] 周鑫美,谢然.基于跌落试验数值仿真的手机耐撞性设计[J].机电一体化,2010(5):69-72.

[3] 彭必友,谢佳斌,冯权和,等.直板手机跌落破坏数字化分析研究[J].西华大学学报(自然科学版),2009(1):74-77.

[4] 祖景平,薛澄岐.手机跌落破坏仿真分析研究[J].中国制造业信息化,2006(11):68-70.

[5] 李鹏忠,张为民,陈炳森,等.机环境试验自由跌落的CAE仿真[J].制造业自动化,2003(8):36-38.

[6] 张纪宽,彭力,陈志勇.基于STM32的双轴监控云台精准控制系统设计[J].单片机与嵌入式系统应用,2016(6):32-35.

[7] 张严林,李海生,钟震宇,等.步进电机三轴联动的快速加减速算法研究[J].微计算机信息,2009(22):111-113.

[8] 陈晔,李兴根.二自由度步进电动机的设计[J].微电机(伺服技术),2005(2):25-28.

[9] 崔洁,杨凯,肖雅静,等.步进电机加减速曲线的算法研究[J].电子工业专用设备,2013(8):45-49.

[10]丁建波,曹将栋.面向跌落仿真的手机外壳注塑成型优化[J].塑料,2012(2):31-33.

[11]陈超,杨毅,李远军,等.一种基于单片机智能控制的云台设计[J].现代电子技术,2011(9):149-152.

[12]李超锋.基于TMS320F240的步进电机加减速控制设计[J].计算机与信息技术,2010(6):33-35.