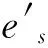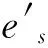一类限位排列的计数*
唐善刚
(西华师范大学数学与信息学院,四川 南充 637009)
Z表示整数集,a是正整数,令[1,a]={1,2,…,a}。设m为正整数,整数
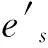
(1)

研究限位排列数的基本方法是棋盘与棋子多项式[5-6],本文利用容斥原理的计数方法[3-5, 7-13]、有限集合上封闭集族的计数方法与其它组合分析技巧的结合研究在阵列(1)下的[1,n]上的如下限位排列的计数[14]。
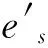
设A表示[1,n]上的所有全排列组成的集合,对任意B⊆A,令f(B)表示集合B的元素个数。对于φ∈A,us∈[1,ns],界定与φ有关的命题Psus(φ)为:
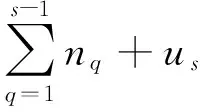
其中1≤s≤m。
令
设Is⊆[1,ns],令

设
非负整数l 本文要用到文献[8]的一个组合恒等式,即下面的引理1。 引理1对于非负整数d,s,t,且s≤t,令 则有 定理1 对于任意的非负整数ts≤ns(1≤s≤m),则有 (2) 证明具体分为3个步骤来完成式(2)的证明。 步骤1 设σs是[1,ns]上的置换,且σs(us)=λus+ds,us∈[1,ns]。根据置换的轮换分解[15],σs恰好分解为(ns,ds)个两两互不相交的ηs-轮换的乘积,由初等数论知识,不难证明σs的ηs-轮换分解为: (3) 于是,阵列(1)基于式(3)的表示为: (4) 其中1≤αs≤(ns,ds),1≤s≤m。 根据阵列(4)与式(3),界定如下的环形排列: ⊙bαs1bαs1bαs2bαs2…bαs (ηs -1)bαs (ηs -1)bαs ηsbαs ηs (5) 对于环形排列(5)中任意取定的元素bαsj,对于φ∈A,根据阵列(4)与环形排列(5),界定与φ有关的命题Pbαsj,bαs(j+1)(φ)与Pbαsj,bαsj(φ)为: 令 其中j∈Z,1≤αs≤(ns,ds),1≤s≤m。 步骤2 在这个步骤中,我们需要证明几个辅助的引理。 根据命题Pbαsj,bαs(j+1)、Pbαsj,bαsj、Psλαs+(j-1)ds与Psλαs+(j-2)ds的界定,显然有如下的引理2成立。 引理2 对于φ∈A,对于环形排列(5)中任意取定的元素bαsj,若命题Pbαsj,bαs(j+1)(φ)成立,则命题Psλαs+(j-1)ds(φ)成立;若命题Pbαsj,bαsj(φ)成立,则命题Psλαs+(j-2)ds(φ)成立。 且 Asλαs+(j-1)ds=Abαsj,bαs(j+1)∪Abαs(j+1),bαs(j+1), Abαsj,bαs(j+1)∩Abαs(j+1),bαs(j+1)=∅; Asλαs+(j-2)ds=Abαsj,bαsj∪Abαs(j-1),bαsj, Abαsj,bαsj∩Abαs(j-1),bαsj=∅ 引理3 从环形排列(5)中选取两个不相邻的元素bαsj1与bαsj2,设环形排列(5)中与bαsj1右相邻的元素为bαs(h1+2),环形排列(5)中与bαsj2右相邻的元素为bαs(h2+2),对于φ∈A,若命题Pbαsj1,bαs(h1+2)(φ)与Pbαsj2,bαs(h2+2)(φ)成立,则命题Psλαs+h1ds(φ)与Psλαs+h2ds(φ)成立,且 证明由引理2,命题Psλαs+h1ds(φ)与Psλαs+h2ds(φ)成立,且有 由环形排列(5),bαs (h1 + 2)=bαs (j1 + 1)或bαsj1;bαs (h2 + 2)=bαs (j2 + 1)或bαsj2,从而 由于bαsj1与bαsj2在环形排列(5)中是不相邻的,则bαsj1≠bαsj2,也即ηs不整除j1-j2。 (i) 当 根据ηs不整除j1-j2,即得 (ii) 当 根据ηs不整除j1-j2,即得 (iii) 当 (iv) 当 综上情况(i)-(iv)所述,即得 由引理3,即得下面的引理4。 引理4 设从环形排列(5)中选取kαs个两两不相邻的元素为bαsjv(1≤v≤kαs),不妨设环形排列(5)中与bαsjv右相邻的元素为bαs(hv+2)(1≤v≤kαs),对于φ∈A,若命题Pbαsjv,bαs(hv+2)(φ)成立(1≤v≤kαs),则命题Psλαs+hvds(φ)成立(1≤v≤kαs),且 y≤kαs,x≠y; (6) 步骤3 以下均约定{bαsjv|1≤v≤kαs}代表的是从环形排列(5)中任意选取kαs个两两不相邻的元素的组合,且约定环形排列(5)中与bαsjv右相邻的元素为bαs(hv+2),其中1≤v≤kαs,1≤αs≤(ns,ds),1≤s≤m。由文献[5,16],这样的组合{bαsjv|1≤v≤kαs}的个数为: (7) 注2 约定从环形排列(5)中选取0个两两不相邻的元素的组合的个数为1,则式(7)对kαs=0也成立。 于是,根据式(6)、式(7)以及引理2与引理4,当0≤kαs≤ηs(1≤αs≤(ns,ds),1≤s≤m)时,即得 (8) 至此,式(2)成立。证毕。 (9) 证明根据容斥原理[8],可得 (10) 将式(2)代入式(10)即得式(9)。证毕。 推论1 对任意非负整数rs≤ns(1≤s≤m),则[1,n]上使得阵列(1)中的第i个阵列中至多有ri个列,它们中的任意列都有相同的数(1≤i≤k),而第j个阵列中恰好有rj个列,它们中的任意列都有相同的数(1+k≤j≤m)的全排列φ的个数为: (11) 推论2 对任意非负整数rs≤ns(1≤s≤m),则[1,n]上使得阵列(1)中的第i个阵列中至少有ri个列,它们中的任意列都有相同的数(1≤i≤k),而第j个阵列中恰好有rj个列,它们中的任意列都有相同的数(1+k≤j≤m)的全排列φ的个数为: (12) 推论3 对任意非负整数rs≤ns(1≤s≤m),则[1,n]上使得阵列(1)中的第i个阵列中至多有ri个列,它们中的任意列都有相同的数(1≤i≤k),而第j个阵列中至少有rj个列,它们中的任意列都有相同的数(1+k≤j≤m)的全排列φ的个数为: (13) 推论4 [1,n]上使得阵列(1)中的任意列都没有相同的数的全排列φ的个数为: (14) (15) 推论6 当(ns,ds)=1(1≤s≤m)时,对任意非负整数rs≤ns(1≤s≤m),则[1,n]上使得阵列(1)中的第i个阵列中至多有ri个列,它们中的任意列都有相同的数(1≤i≤k),而第j个阵列中恰好有rj个列,它们中的任意列都有相同的数(1+k≤j≤m)的全排列φ的个数为: (16) 推论7 当(ns,ds)=1(1≤s≤m)时,对任意非负整数rs≤ns(1≤s≤m),则[1,n]上使得阵列(1)中的第i个阵列中至少有ri个列,它们中的任意列都有相同的数(1≤i≤k),而第j个阵列中恰好有rj个列,它们中的任意列都有相同的数(1+k≤j≤m)的全排列φ的个数为: (17) 推论8 当(ns,ds)=1(1≤s≤m)时,对任意非负整数rs≤ns(1≤s≤m),则[1,n]上使得阵列(1)中的第i个阵列中至多有ri个列,它们中的任意列都有相同的数(1≤i≤k),而第j个阵列中至少有rj个列,它们中的任意列都有相同的数(1+k≤j≤m)的全排列φ的个数为: (18) 推论9 当(ns,ds)=1(1≤s≤m)时,[1,n]上使得阵列(1)中的任意列都没有相同的数的全排列φ的个数为: (19) 注3 式(17)推广了文献[3]的结果,文献[4]试图推广文献[3]的结果,但文献[4]的结果被证明是错误的[7],式(17)是对文献[4]的错误结果的改正与推广,式(9)则是对阵列(1)中的ns>(ns,ds)≥1(1≤s≤m)情形下的结果的统一回答。 (20) 由于ft1,…,tm在阵列(1)中的计算方法并不适用于阵列(20),从而导致ft1,…,tm在阵列(20)中的显式计算公式很难获得,关于这一点可以参阅文献[5],本文未能得到问题Ⅱ的显式计数公式,仅仅得到δs=1(1≤s≤m)对应的问题Ⅰ的显式计数公式,即式(9),我们将在后续的研究中尝试寻求ft1,…,tm在阵列(20)中的显式计算公式的方法。 参考文献: [1] 魏万迪. 限位排列和k一积和式 [J]. 应用数学学报,1983, 6(2): 177-182. WEI W D. Permutations with restricted positions andk-permanent [J]. Acta Mathematicae Applicatae Sinica, 1983, 6(2): 177-182. [2] 张福基,张遴贤,林治勋. 限位排列的一个图论方法 [J]. 应用数学学报,1983,6(2): 240-246. ZHANG F J,ZHANG L X,LIN Z X. A method of graph theory for restricted permutations [J]. Acta Mathematicae Applicatae Sinica,1983, 6(2): 240-246. [3] 魏万迪. 广容斥原理及其应用 [J]. 科学通报,1980, 25(7): 296-299. WEI W D. A generalized principle of inclusion-exclusion and its applications [J]. Chinese Science Bulletin, 1980, 25(7): 296-299. [4] 万宏辉. 容斥原理的拓广及其应用 [J]. 科学通报,1984, 29(16): 972-975. WAN H H. A generalized principle of inclusion-exclusion and its applications [J]. Chinese Science Bulletin, 1984, 29(16): 972-975. [5] STANLEY R P. Enumerative combinatorics: Volume 1 [M]. Cambridge: Cambridge University Press,1997. [6] 唐保祥,任韩. 3类特殊图完美匹配数的计算公式 [J]. 中山大学学报(自然科学版),2017, 56(3): 36-40. TANG B X,REN H. The counting formula of the perfect matchings of three types of special graphs [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2017, 56(3): 36-40. [7] 唐善刚. 关于“容斥原理的拓广及其应用”的注记 [J]. 山东大学学报(理学版),2012, 47(10): 64-69. TANG S G. A note on “generalized principle of inclusion-exclusion and its application” [J]. J Shandong University (Natural Science), 2012, 47 (10): 64-69. [8] 唐善刚. 广义容斥原理及其应用 [J]. 山东大学学报(理学版),2009, 44(1): 83-90. TANG S G. Generalized principle of inclusion-exclusion and its application [J]. J Shandong University (Natural Science), 2009, 44(1): 83-90. [9] 唐善刚. 容斥原理的拓展及其应用 [J]. 山东大学学报(理学版),2010, 45(12): 12-15. TANG S G. A generalization of principle of inclusion-exclusion and its application [J]. J Shandong University (Natural Science), 2010, 45(12): 12-15. [10] 唐善刚. 容斥原理的拓展及其应用(Ⅱ) [J]. 山东大学学报(理学版), 2011, 46(12): 70-75. TANG S G. A generalization of principle of inclusion-exclusion and its application (Ⅱ) [J]. J Shandong University (Natural Science), 2011, 46(12): 70-75. [11] 曹汝成. 广义容斥原理及其应用 [J]. 数学研究与评论,1988, 8(4): 526-530. CAO R C. A generalized principle of inclusion-exclusion and its applications [J]. J Mathematical Research and Exposition, 1988, 8(4): 526-530. [12] 唐善刚. 赋权有限集上的容斥原理及应用 [J]. 浙江大学学报(理学版),2014, 41(2): 123-126. TANG S G. A principle of inclusion-exclusion on a weighted finite set and its applications [J]. J Zhejiang University (Science Edition), 2014, 41(2): 123-126. [13] BENDER.E A, GOLDMAN J R. On the applications of mobius inversion in combinatorial analysis [J]. Amer Math Monthly, 1975, 82(8): 789-803. [14] 唐保祥,任韩. 有限集合上封闭集族的计数 [J]. 中山大学学报(自然科学版),2010, 49(6): 11-14. TANG B X,REN H. Enumeration of closed family of finite sets [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2010,49(6) : 11-14. [15] 韩士安,林磊. 近世代数 [M]. 北京: 科学出版社, 2004. [16] 李磊. 关于几个组合计数公式的推广 [J]. 工程数学学报,1996,13(4) : 95-98. LI L. Generalization of some combinatorial formulas [J]. J Engineering Mathematics,1996,13(4): 95-98.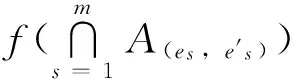
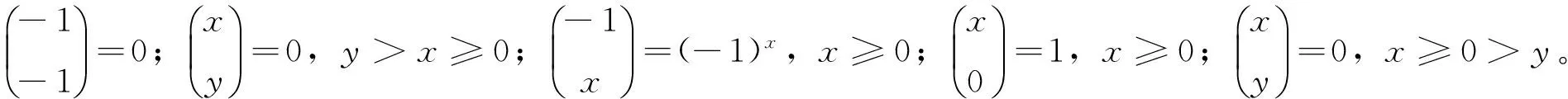
1 ft1,…,tm的显式计算公式
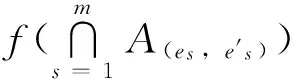
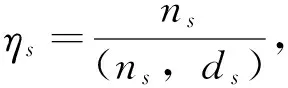
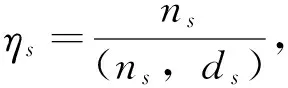


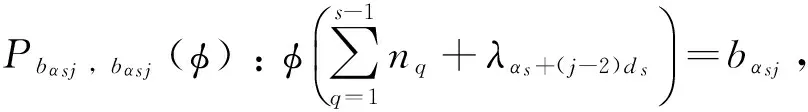


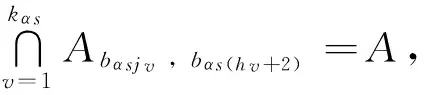
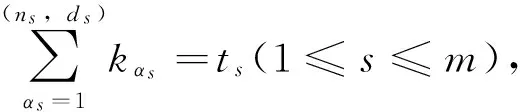
2 主要结果
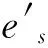
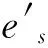
3 讨 论