对于高层框架结构与桩筏基础共同作用的整体研究

祝　峰

(中铁十八局集团有限公司，天津 300222)

0　引言

高层建筑的上部结构、基础和地基是一个统一的有机整体，三者相互联系、相互影响。目前对于高层建筑桩筏基础共同作用的研究已取得了一些成果，但由于高层建筑桩筏基础是一个十分复杂的系统，其共同作用的研究涉及众多因素，以前，人们对其工作机理的认识还不够清楚，因此，进一步地深入研究高层框架结构—桩筏基础—地基的共同作用，使高层建筑设计既安全又经济合理，具有重要意义。

随着计算机技术和数值方法的发展，许多有限元软件被用于高层结构数值模拟，如Abaqus、ANSYS、Canny等。彪仿俊等[1]采用Abaqus对空中华西村进行整体三维建模分析，为基础设计和验算提供了更为可靠的数值依据。虽然现阶段国内外学者对高层建筑的研究已经取得了较为丰富的成果，但在工程中仍然需要一些定量的分析来指导高层框架结构的设计。本文通过分析高层框架结构的荷载与桩土接触方式，确定荷载与接触类型。基于有限元软件Abaqus对上部框架—桩筏基础—地基共同作用体系进行模拟分析，结果表明，与非共同作用比较,共同作用体系与实际情况更加相符，可为该类建筑的设计提供参考。

1　荷载分析与桩土接触方式

1.1　高层框架结构荷载

高层框架结构的设计荷载作用包括3类，分别为竖向荷载、风荷载与地震作用[2]。竖向荷载由结构自重与等效均布活荷载组成。风荷载作用下，高层建筑考虑上部结构—基础—土作用的分析是一个复杂的系统问题，涉及流体动力学、结构动力学、土力学等方面[3]。高于40 m的建筑可采用振型分解反应谱法[4]进行水平地震荷载计算，各层的水平地震力等效为线荷载。由于风荷载的复杂性，只分析竖向荷载与地震作用下框架—桩筏基础—地基共同作用体系的受力情况。地震作用是指地震波从震源通过基岩传播引起地面运动，从而引起地表及其上的建筑物、构筑物等的强烈振动。地震作用具有随机性大(时间、大小)、作用时间短、破坏性强、重现期不同等特点，难于精确计算和准确预测。

1.2　桩土接触方式

在分析桩基与土相互作用时，采用弹塑性地基模型求得的群桩基础沉降性状与实测结果更加接近。土体假定为弹塑性材料，符合Mohr-Coulomb屈服准则。

Mohr-Coulomb模型主要适用于单调荷载下的颗粒状材料，屈服面的表达式为：

F=Rmcq-ptanφ-c=0，

(1)

式中：c为内聚力；φ为内摩擦角；Rmc为极偏角Θ和内摩擦角φ的函数；q为Mohr-Coulomb模型的屈服面在π平面的形状为不光滑的尖角六边形，如图1所示。

π平面形状的表达式为：

(2)

式中：Θ为极偏角；φ为内摩擦角。

图1　π平面上的Mohr-Coulomb准则示意图

流动准则在尖角处由于流动方向的不确定性而容易不收敛，因此，Abaqus中采用光滑的曲面来代替原来的六边形作为势能面。

群桩分析时要考虑群桩效应的影响，在分析时采用弹性理论法。桩体和土体之间设置接触单元进行传力和约束，采用主—从接触算法，土定义为从面。接触面间的相互作用分为法向作用和切向作用两部分：法向作用采用的是“硬”接触，这种模型假定接触面之间的间隙≤0时才会产生接触压力；切向作用采用罚函数摩擦，即根据接触面上单元的长度确定弹性滑移变形，然后选择罚函数计算此方法中的刚度。

2　工程应用

2.1　工程概况

某高层建筑抗震设防烈度为7度，场地类别为第2类，地震设计分组为第2组。上部结构为18层框架结构，层高均为3 m，框架柱截面尺寸为0.8 m×0.8 m，框架梁截面尺寸为0.35 m×0.7 m，楼板厚度均为0.12 m。混凝土等级均为C30。建筑结构平面布置图如图2所示。

图2　建筑结构平面布置图

下部基础形式为桩筏基础，均匀布桩，桩的间距为3 m，直径为0.6 m，长度为16 m，筏板厚1 m，尺寸为18 m×45 m，即四周由边柱圆心挑出1.5 m。混凝土等级均为C30。桩周土层主要为褐黄色粉质黏土，桩端土层主要为暗绿色粉质黏土。

2.2　有限元模型

2.2.1单元与边界

基于对称性，取半结构进行建模分析。上部的梁、柱为钢筋混凝土整体式模型，采用梁单元模拟。楼板与筏板均采用一般性壳单元模拟，桩和土体均采用实体单元模拟。地基土尺寸为54 m×41 m×30 m，为满足计算精度与计算效率的要求，网格尺寸随着与桩的距离增大而增大，如图3所示。

图3　桩和土有限元模型 桩间距为3.0 m×3.0 m

楼板与梁柱之间通过绑定进行连接，柱与筏板、桩与筏板也是绑定连接。桩、筏板与土的切向摩擦系数均为0.2。地基土侧面约束法向位移，底面约束各向位移。

2.2.2材料参数

钢筋混凝土结构工作状态处于弹性，弹性模量根据复合材料的确定方法确定，各构件的计算参数见表1。

表1　钢筋混凝土构件的计算参数

根据该地区典型的土层分布情况，各个土层的主要物理力学参数指标见表2。

2.3　计算工况

上部结构由梁、柱、楼板组成，下部结构由筏板、桩、土组成。计算工况分为非共同作用与共同作用两个工况。楼层活荷载为2 kN/m2，水平地震作用采用振型分解反应谱法进行简化计算。

工况1为非共同作用：首先，分别建立上部结构模型和下部结构模型，不考虑相互作用。上部结构中，底层柱子底端采用固接的形式；下部结构中，筏板和土体顶面为自由边界。然后，施加荷载并得出底层柱底轴力和弯矩，将结果施加在下部桩土模型上，得到下部结构的内力及变形情况。

表2　土层的主要物理力学参数

工况2为共同作用：将上部结构和下部结构连为一个整体，考虑相互作用。施加荷载后，得出内力和变形情况。

3　共同作用的影响

3.1　下部结构的影响

工况1与工况2中的地基最大沉降量分别是21.5 mm、12.0 mm，二者差距较大。沿筏板A轴长度方向，共同作用相比非共同作用，筏板中部沉降量要小，而边缘相反，如图4所示。两种工况中，筏板的沉降均呈现“凹形”分布，即中部沉降较大，边缘沉降较小。

图4　筏板A轴沉降图

两种工况中，筏板在中间位置的弯矩Mx比边缘位置的要大，如图5所示。这是由于中间位置的变形比较大，筏板弯曲得较为严重。在筏板中部，两种工况的弯矩Mx有一定差别，在边缘处两种工况所得结果基本相等，如图6所示。

3.2　上部结构的影响

共同作用相对非共同作用，各层层高处总位移增加较大，随层数的增加近似呈线性增长。各层层间位移相对增大3～4倍。这是由于不均匀沉降引起上部结构底部转角，从而导致较大的侧向位移。

图5　5轴筏板弯矩Mx图

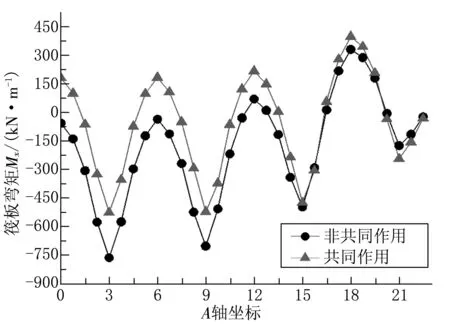
图6　A轴筏板弯矩Mx图

两种工况中，角柱和中柱的各层柱底轴力差别较大，如图7～8所示。考虑共同作用时，底层角柱柱底轴力增大410 kN，底层中柱柱底轴力减小540 kN。对于离角柱较近的边柱和离中柱较近的次边柱影响不大。共同作用的影响随层数的增加而减弱，对底层柱底轴力的影响最大，而对顶层柱底轴力基本无影响。

4　结语

1)利用Abaqus软件进行建模，结果表明，计算模型和方法能够很好地模拟静力作用下高层框架结构—桩筏基础—地基的受力变形情况。

2)通过比较共同作用与非共同作用对结构的影响，共同作用模型受力更加合理，与实际情况更加相近。

3)通过改变模型中上部框架层数、地基弹性模量、桩长、桩径及筏板厚度，分析各因素对结构的影响，可为该类建筑提供设计依据。

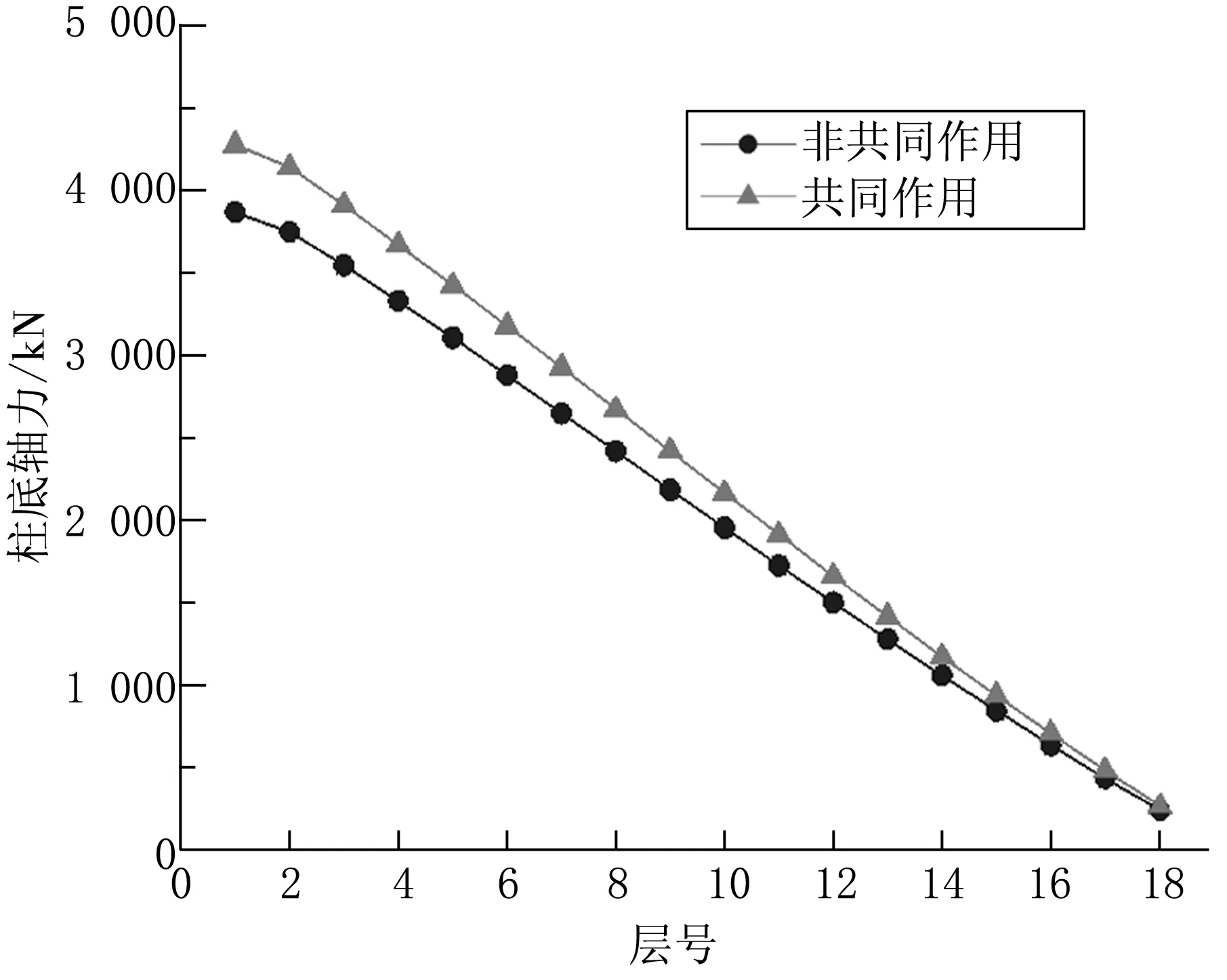
图7　各层柱底轴力图(角柱轴力图)

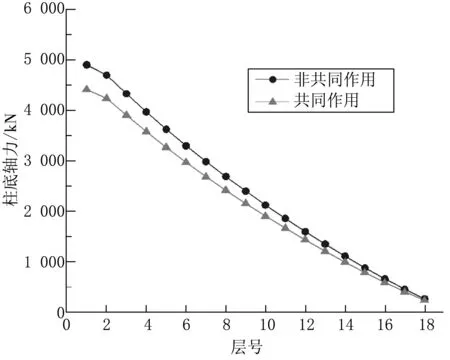
图8　各层柱底轴力图(中柱轴力图)

[1] 彪仿俊，王传甲，薛炳，等.空中华西村结构与桩筏共同作用研究[J].建筑结构，2009，38(8):123-126.

[2] 徐培福，王翠坤，肖从真.中国高层建筑结构发展与展望[J].建筑结构，2009，39(9):28-32.

[3] 宿金成.风致高层建筑地基破坏模式研究[D].哈尔滨：哈尔滨工业大学，2013.

[4] 李爱群，丁幼亮.工程结构抗震分析[M].北京:高等教育出版社，2010.