不同角度斜柱的钢框架结构静力稳定性分析
赵丽芝
(长春工程学院土木工程学院,长春 130012)
0 引言
近年来,斜柱受到越来越多设计师的青睐,使得带斜柱的建筑明显增加[1]。如何正确选取斜柱的倾斜角度成为建筑设计中的难题,因此,斜柱倾斜角度对结构影响的研究十分重要。国内外学者对带斜柱建筑的研究侧重于斜柱构件本身,关于斜柱对结构性能影响的研究较少[2-5]。本文利用有限元软件SAP2000建立钢框架模型,并通过改变模型中斜柱的倾斜角度,分析和研究斜柱对钢框架结构静力稳定性的影响。
1 模型建立
首先,用有限元分析软件SAP2000建立模型M1。M1模型中一个6层钢框架结构,各层层高均为5.4 m,总高20.4 m,表1给出了模型M1中梁柱的具体截面尺寸。模型中,A轴线上所有柱子为斜柱,倾斜角度为5°(倾斜角度为柱子与铅垂线间的角度),斜柱高度至3层(16.2 m)。
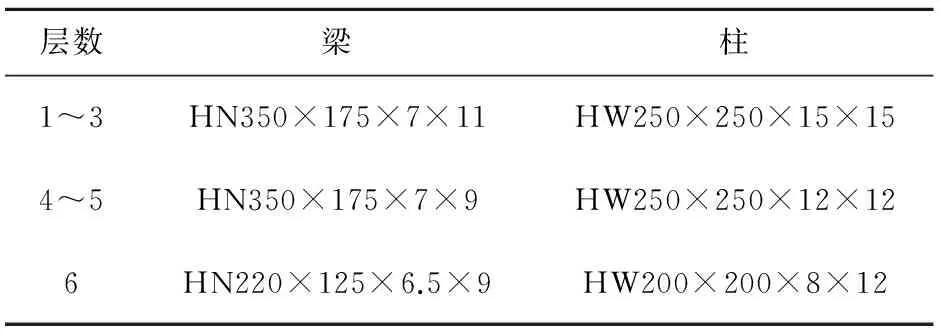
表1 模型梁、柱截面尺寸
M2模型和M3模型是将M1模型中所有的斜柱的倾斜角度分别修改为10°和15°,其余均与M1相同。图1~3分别给出了模型M1、M2和M3的三维视图。
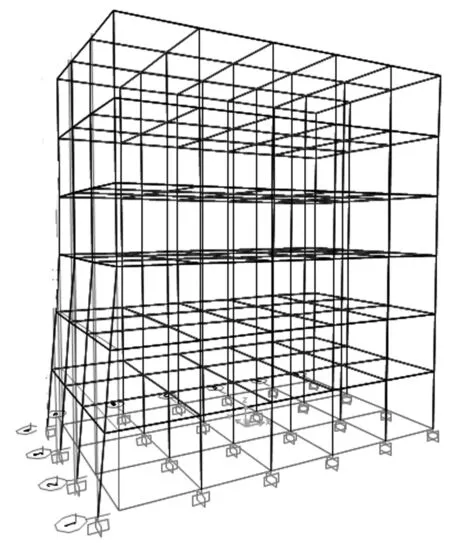
图1 M1三维视图

图2 M2三维视图

图3 M3三维视图
2 稳定性判别准则
结构失稳一般分为两类:第一类是理想的情况,即当结构达到某荷载值时,结构除了原有的平衡状态外,还可能存在第二种平衡状态,所以又称平衡分岔失稳或分支点失稳,由于其在数学处理上是求解特征值的问题,故又称为特征值屈曲。第二类失稳是指结构失稳时,变形迅速增大,不会出现新的变形形式,即平衡状态不会发生质变,又称为极值点失稳。本文的稳定性分析考虑了结构的初始缺陷、几何非线性以及材料非线性,属于第二类失稳[6]。
对于结构整体稳定性判别准则,文献[7]指出对于整体稳定性准则有以下3个观点:1)荷载—位移曲线顶点判定准则;2)承荷载极限判定准则;3)荷载—位移曲线斜率判定准则。
本文采用第2)种判别准则,给结构逐级加载,直到结构无法承受为止,认为此时为结构的稳定临界状态,对应的荷载为结构的静力极限荷载。
3 稳定性分析
3.1 荷载组合
静荷载的设计组合有多种,考虑的荷载主要包括结构自重、墙体重量(折合成线荷载施加在梁上)、活荷载以及X向风荷载,取基本风压值0.45 kN/m2,地面粗糙度为B类,风荷载体形系数μs=1.3。
3.2 特征值屈曲分析
特征值屈曲分析在分析过程中不考虑结构的初始缺陷和非线性属性,因此,它的屈曲荷载可近似代表相应的第二类稳定问题的上限,所以在求解结构的极限荷载之前,一般先对结构进行一次特征值屈曲分析。采用有限元分析软件SAP2000对结构进行特征值屈曲分析后,可以得到不同模态下的特征值屈曲因子λ,λ与施加在结构上的荷载的乘积才是我们所说的屈曲荷载大小。
由于结构的永久荷载为结构自重及墙身重量,是结构的固有荷载,因此在屈曲分析中只对结构施加活荷载和风荷载,但是需要将初始条件设置为恒荷载非线性工况之后。
上述荷载作用下结构屈曲分析的前三阶屈曲模态如图4所示。

(a)一阶屈曲模态

(b)二阶屈曲模态

(c)三阶屈曲模态图4 M1的前三阶屈曲模态
由图4可知,无论哪种模态,结构的顶层位移都是最大的,取顶层节点147(30 m,12 m,20.4 m)为观察点来确定达到极限荷载作用时结构的最大位移。表2列出了结构M1、M2的前三阶模态特征值屈曲因子值。

表2 M1、M2特征值屈曲因子
通常情况下,将结构第一振型的特征值屈曲因子与基本荷载的乘积作为结构的屈曲荷载。从表2可以看出,在理想情况下,模型M1可以承受的最大荷载为:1×恒荷载+1×楼层荷载+135×(活荷载+风荷载);M2模型可承受的最大荷载为:1×恒荷载+1×楼层荷载+136×(活荷载+风荷载);M3模型可承受的最大荷载为:1×恒荷载+1×楼层荷载+134×(活荷载+风荷载)。以此为模型M1、M2和M3的荷载上限对结构进行非线性屈曲分析。
3.3 非线性屈曲分析
工程实际中不可避免地存在初始缺陷,结构的几何非线性和材料非线性对结构的影响也是客观存在的。所以,要想得到结构的极限承载能力,还需要进行结构的非线性屈曲分析。
将模型M1的比例参数设置为136,荷载子步设定为272步,即每一个子步对应0.5倍的基本荷载;将M2的比例参数设置为137,荷载子步也设定为274步;将M3的比例参数设置为135,荷载子步也设定为270步。分别对M1、M2和M3进行非线性屈曲分析,得到各自的荷载子步—位移曲线,如图5。由图5可以得出以下结论:
1)模型M1在前32步的加载过程中,结构的荷载位移关系曲线大致为直线,说明结构还处于弹性阶段;再继续加载到基本荷载33步时,荷载位移曲线变弯曲,斜率呈现增大趋势,结构的刚度逐渐变小;当承受的外力增加到39步时,结构的刚度迅速减小,分析停止,根据第二类稳定性判定准则可知此时结构丧失了稳定性,结构的最大位移为0.29 m。因此,可以认为模型M1的极限荷载为39×0.5=19.5倍的基本荷载。
2)模型M2在前32步的加载过程中,结构的荷载位移关系曲线大致为直线;再继续加载到基本荷载33步时,荷载位移曲线变弯曲,结构的刚度逐渐变小;当荷载增加到42步时,结构的刚度迅速减小,同时分析停止,根据第二类稳定性判定准则可知此时结构丧失了稳定性,结构的最大位移为0.29 m。因此,可以认为模型M2的极限荷载为42×0.5=21倍的基本荷载;同理可以得出,M3的极限荷载为18倍的基本荷载,结构的最大位移为0.35 m。

(a)M1荷载位移曲线图

(b)M2荷载位移曲线图

(c)M3荷载位移曲线图图5 模型荷载位移曲线图
3)钢框架结构的稳定性并不是随着斜柱角度的增大而提高,当斜柱的倾斜角度增大到一定值时,钢框架结构的稳定性反而会明显降低。
3.4 斜柱倾斜角度与结构稳定性关系
通过以上的分析可知,斜柱的倾斜角度与钢框架结构的稳定性之间并不是正比例的关系。分别建立模型M4~M11,模型中斜柱的倾斜角度依次为6°、7°、8°、9°、11°、12°、13°和14°,分别对他们进行特征值屈曲分析与非线性屈曲分析,得出各自的极限承载能力,见表3。

表3 斜柱倾斜角度与模型极限承载能力
为了更直观地表达分析结果,将表3的数据绘制成图6所示的折线图。

图6 斜柱倾斜角度与模型极限承载能力关系图
由图6可以看出,此钢框架结构在斜柱倾斜角度小于13°时,结构的极限承载能力随着斜柱倾斜角度的增大而缓慢提高,当斜柱的倾斜角度大于14°时,钢框架结构的静力稳定性显著下降。可知,对于本钢框架结构静力稳定性而言,合适的斜柱倾斜角度为13°。
4 结语
本文利用有限元软件SAP2000分析研究了斜柱的倾斜角度对钢框架结构静力稳定性的影响,通过分析得到模型M1、M2以及M3在静荷载作用下的荷载位移曲线,对比发现钢框架结构的稳定性并不是随着斜柱角度的增大而提高,而是呈抛物线型,即当斜柱的倾斜角度增大到一定值时,钢框架结构的稳定性反而会明显降低。
[1] 容柏生.国内高层建筑结构设计的若干新进展[J].建筑结构,2007,37(9):1-5.
[2] 王永春,丁洁民.斜柱超高层筒中筒结构的受力特性研究[C]//第18届全国高层建筑结构学术交流会论文集(上册).北京:中国建筑科学研究院,2004:333-338.
[3] 傅剑平,程思聪,黄宗瑜.钢管混凝土斜柱抗剪环-环梁节点抗震性能试验[J].重庆大学学报,2008,31(3):349-354.
[4] 马凯.超限倾斜结构的弹塑性动力分析[J].动力学与控制学报,2011,9(3):253-256.
[5] 刘庆林,傅学怡,曹敏丽,等.体型收进斜撑转换结构研究应用——珠海信息大厦高位收分转换解析[J].土木工程学院,2006(2):6-10.
[6] 董庆.高层钢框架结构整体稳定性研究[D].南京:南京林业大学,2012.
[7] 王旭,张威,甘为众,等.钢框架整体稳定判定准则研究[J].科技创业月刊,2006,10(3):230-232.

