基于层次分析法与模糊物元分析的城市充电站选址决策方法

王 哲，殷帅兵，王军生，周继尧



基于层次分析法与模糊物元分析的城市充电站选址决策方法

王 哲1，殷帅兵1，王军生1，周继尧2

(1.许继电气股份有限公司, 河南 许昌 461000； 2.河北工业大学, 天津 300401)

为了提升城市充电站选址的科学性，提高城市电力运营效益，改善城市交通的运营状况，将层次分析法与模糊物元法进行结合，并将其应用于城市内电动汽车充电站选址的综合决策中。利用层次分析法(AHP)将有关因素对城市内电动汽车充电站影响的大小程度转换为权重，并通过模糊物元方法对多个候选方案建立多维复合模糊物元矩阵。经过关联变换将不相容的问题转化为相容问题，从而为多个充电站备选方案的综合评价做出定量的分析，为充电站选址最优化提供数据依据。结果表明：运用层次分析法与模糊物元分析相结合的方法所得到的结果与运用传统的选址模型得到的结果趋于一致。结果证明了这种方法的合理性和科学性，为城市充电站选址规划提供了一种简便、科学的实用性方法。

层次分析法；模糊物元分析；电动汽车；充电站；最优决策

0 引言

市内电动汽车充电站因为在节省占地面积、帮助电网削峰填谷等方面拥有无可比拟的优势[1]，在日后必将作为电动汽车在城市内的主要能源来源，并在社会经济活动中发挥重要的作用[2]。充电站的选址科学与否将直接影响到电力运营效益[3]，也会对城市交通的运营产生重要的影响。因此，在进行充电站选址、规划与建设时，必须对充电站的选址方案进行决策分析，合理确定城市电动汽车充电站的位置、规模，从而构建经济合理、运行安全、运营高效的充电站网络。

现在运用较多的方法是在已有充电桩的基础上，采用0-1规划及覆盖的数学模型对充电桩的位置进行分配，采用动态调整与静态增设的方法，使目标函数(即通过规划后的电动汽车充电桩的利用率)最大，从而确定充电桩的合理选址位置。但是这种方法不能通过定量分析来对多个方案作出综合评价。层次分析法和模糊数学越来越多地被应用到各个领域中。通过将层次分析法和模糊数学应用到充电站的选址问题中，来提高充电桩选址的准确度，为多个充电站备选方案的综合评价做出了定量的分析，也为充电站选址最优化提供了数据依据。

层次分析法通过计算判断矩阵的最大特征值与特征向量，得到各层次要素对于上层要素的重要性次序，从而建立权重向量。但由于判断时往往夹杂着主观性与片面性，所得到的判断矩阵不一定可以通过一致性检验，并且采用1-9级法往往使得专家在构建判断矩阵时较难下手。后期如果不通过一致性检验对矩阵进行调整又极易影响专家判断。本文采用了三级标度法改进层次分析法，对各层因素进行两两判断，建立比较矩阵，计算最优传递矩阵，确定判断矩阵，得到权重[4-7]，并与模糊物元方法结合，从而构建充电站的选址决策模型。

1 城市充电站选址规划影响因素分析

依据电动汽车充电站的选址体系建设，需要考虑的因素很多。根据目前所开展的大量电动汽车相关研究来看，影响电动汽车充电站选址规划的主要因素有交通因素、经济因素、技术因素和综合因素[8-10]。采用德尔菲(dephi)方法让专家们对最初构建的评价体系进行独立不交流的评价，并收集反馈意见，确定评价体系中的准则层与目标层因素[11-12]。

2 综合评价体系的建立

2.1 建立递阶层次结构模型

将众多的相互影响的因素按照一定顺序互相配合，上下隶属关系分成不同层次，用线段将下层因素和上层因素相连接，则可以整理成有序的递阶层次结构。该结构通常分为三个层次：自下而上分别是方案层、准则层与目标层，如图1所示。

2.2 构造判断矩阵

传统的层次分析法是借助1-9级方法将隶属于同一层因素的所有因素进行两两相互比较，按照重要性排序。实际应用中，由于人为判断的主观性与片面性，所得结果往往不具有客观一致性，不能通过客观一致性检验，往往需要通过一些修正方法对其进行修改，如：手工调整法、迭代法、对数最小二乘法等。利用最优传递矩阵对常规的层次分析法进行改进后，使之自然满足一致性要求，不需要进行一致性检验[13-14]，简化了两两比较时的复杂过程。

2.2.1最优传递矩阵原理

三标度矩阵改进的层次分析法对于传统的层次分析法的改进在于引入最优传递矩阵，通过先求出与该最优传递矩阵具有一致性的拟优化传递矩阵，最后由该最优传递矩阵的拟优化传递矩阵求出评价因素的权重值。

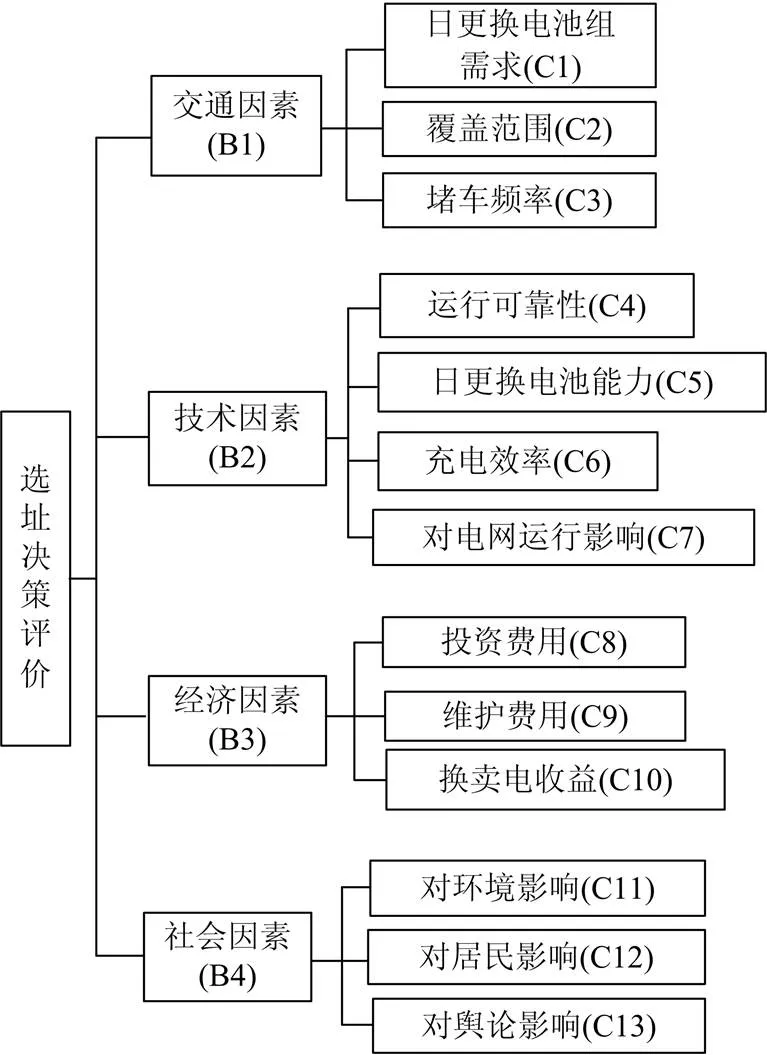
图1电动汽车充电站选址因素的递阶层次结构图

Fig 1 Hierarchical hierarchy graph for electric vehicles charging stations site selection factors

设实数矩阵=[a],=[b],=[c],若是反对称矩阵，则的最优传递矩阵应该满足

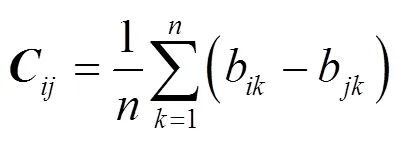
2.2.2最优传递矩阵计算

给出在每一层次上各元素之间重要性程度的三标度比较矩阵。

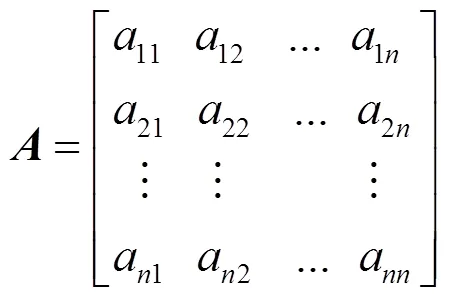
计算最优传递矩阵。

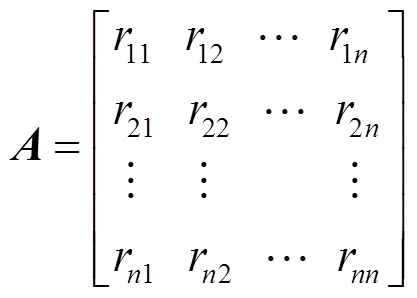
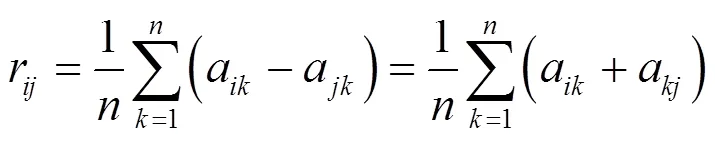
把矩阵转换成一致矩阵(判断矩阵)

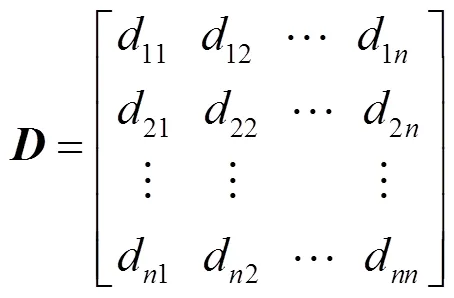
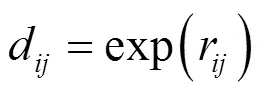
将数据经过式(3)至式(6)后得到以下矩阵。

2.3 层次排序

层次单排序是指由判断矩阵计算该层要素关于相邻一层次要素的优先权重。可以归结为计算中最大特征值所对应的特征向量，即满足

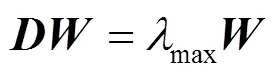
本文采取和法计算特征值向量，其计算过程可以表示成如下的矩阵变换形式。

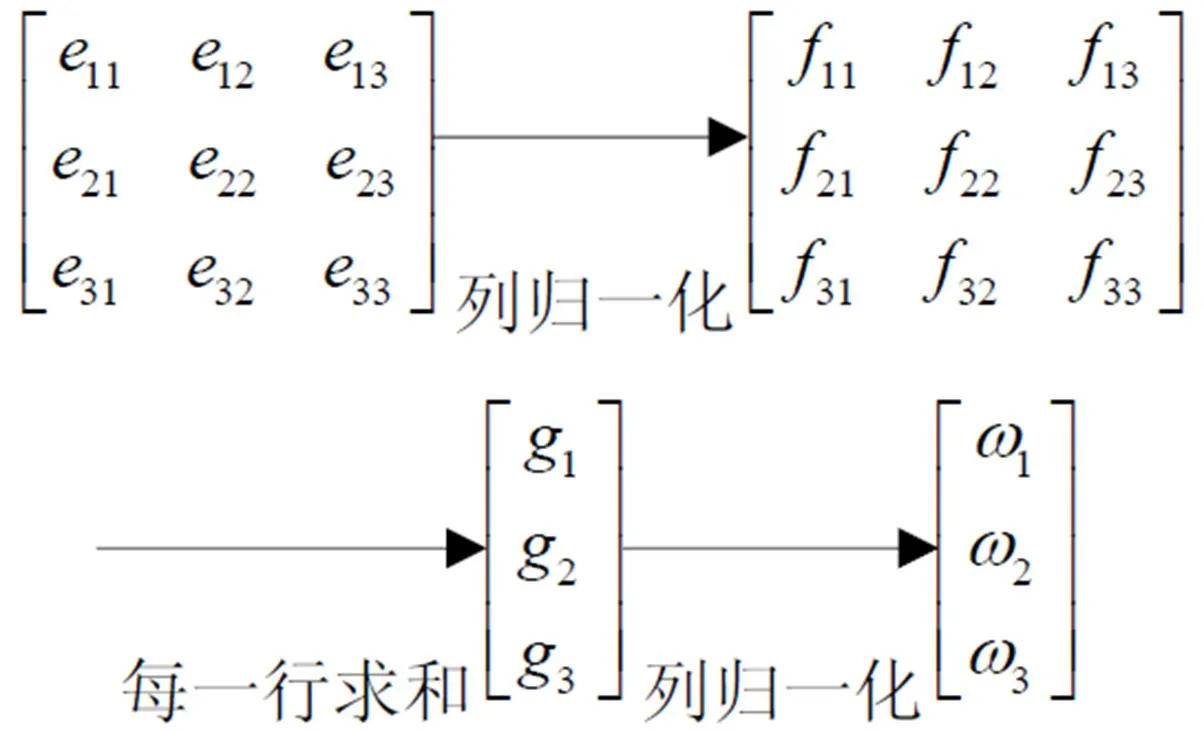
排序完成后，得到所有层次对于上一层的影响权重值，如表1所示，进行层次总排序即可得出方案层因素对于目标层的影响。层次总排序是指计算同一层所有要素对于最高层相对重要性的排序权值[18]，计算方法与传统的层次分析法相同。按照上述方法对每个专家给出的数据进行处理并取平均值后得出如表1所示的权重数据。

表1各个层次的影响权重

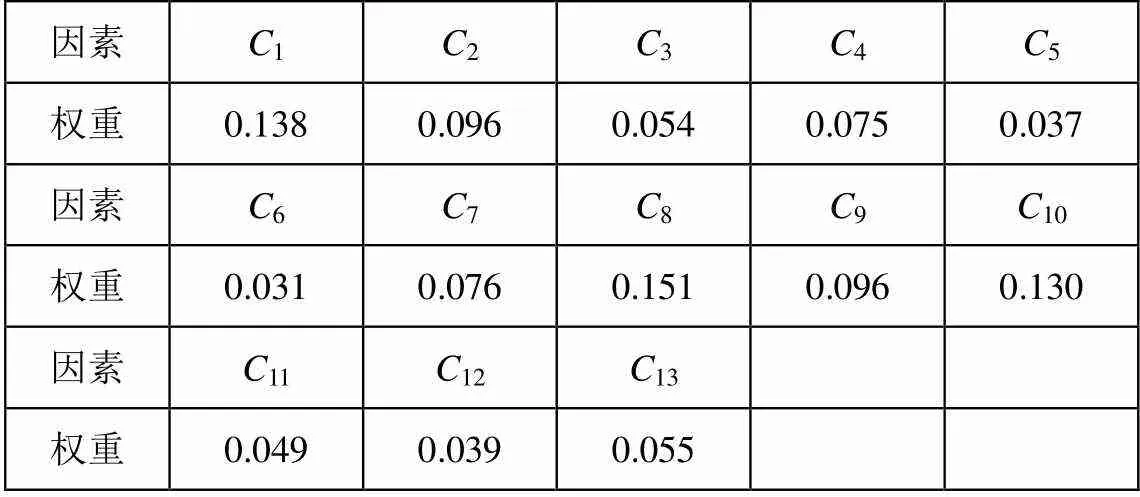
Table 1 Effect weight of all levels

3 基于模糊物元分析城市充电站选址决策模型

物元分析是解决不相容问题规律和方法的新兴学科，通过此方法可以将事物用“事物、特征、量值”三个要素描述。如果物元中的量值具有模糊性，便构成了模糊不相容问题，为了解决这方面的问题，将物元分析和模糊数学有机地结合起来，这种新的方法叫做模糊物元分析法[19-21]。基于该类分析，建立城市充电站选址决策模型。本文得到了某市五个充电站的备选方案数据如表2所示，根据AHP方法与模糊物元法将对其做出最优化决策。

为了消除各个因素量纲不同的影响，在得到备选方案的详细信息后将其送给专家并进行30分制的量化打分，各个因素均采取有利于电网稳定以及电动汽车发展则分高的原则。表3为专家组对某市5个备选方案的各个因素的平均评分。

3.1 建立模糊物元矩阵

模糊物元分析是指用“事物、特征、模糊量值”来描述事物的基本元[22]。模糊物元用符号表示为

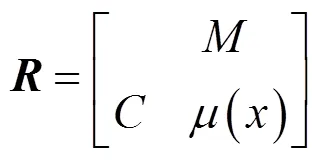
式中：表示选址的方案编号；表示一些特征，例如入站充电的车流量等；()表示与事物特征相应量值的隶属度。

3.2 将模糊物元矩阵变化为隶属度矩阵

将模糊物元矩阵变化为隶属度矩阵需要引入从优原则，本文中所选取的从优原则如式(9)—式(11)所示。

最大原则：

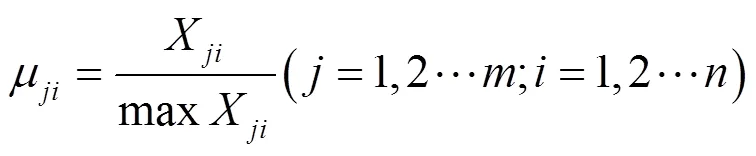
最小原则：

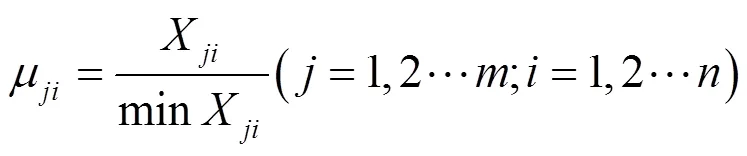
最接近原则：

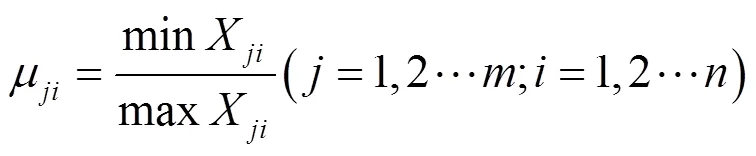
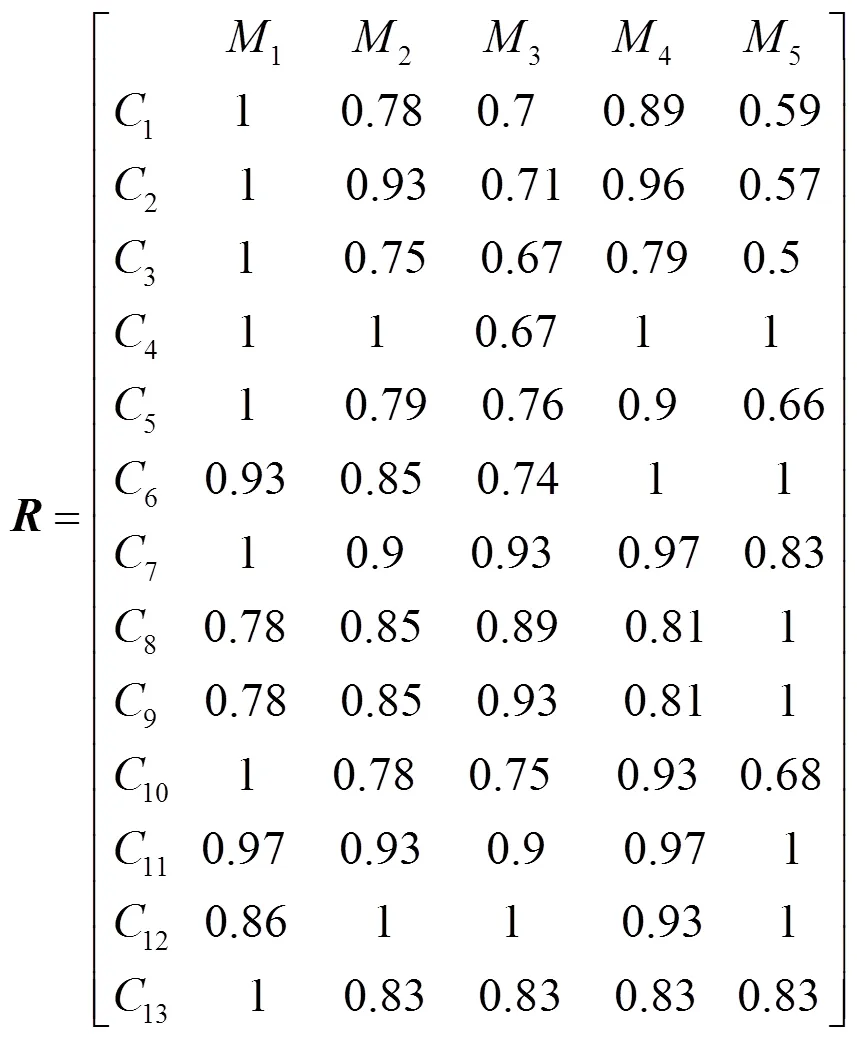
本文为了避免量纲干扰评价，对各种数据的综合成绩进行了打分处理，根据各个指标对电网运行以及电动汽车的影响，有利则分高，有害则分低，即对所有因素均采取最大原则。运用最大原则后的模糊物元矩阵如式(12)所示。

3.3 计算关系函数

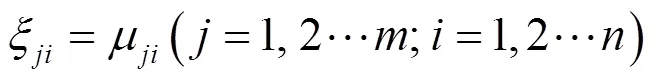
3.4 求关联度向量

因为每个备选方法都有(=13)个不同的系数，除非某个方案的系数都比别的方案更为优，否则想要一眼看出各个方法哪个最好是不现实的。若以表示每一个方案各评价指标的权重复合物元，以表示由个关联系数组成的关联度复合模糊物元，采用加权平均处理，如式(14)所示。

其中，*表示运算符号，由于本文的优化模式选取的为模式一，所以该运算在此表示M(•,+)，运算方式类似于矩阵乘法，为了将所有的因素权重都参与运算，这里采用的方法为M(°,+)，计算后的关联度包括所有因素的共同作用。

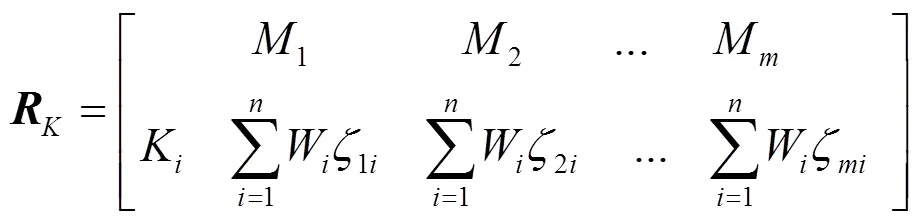
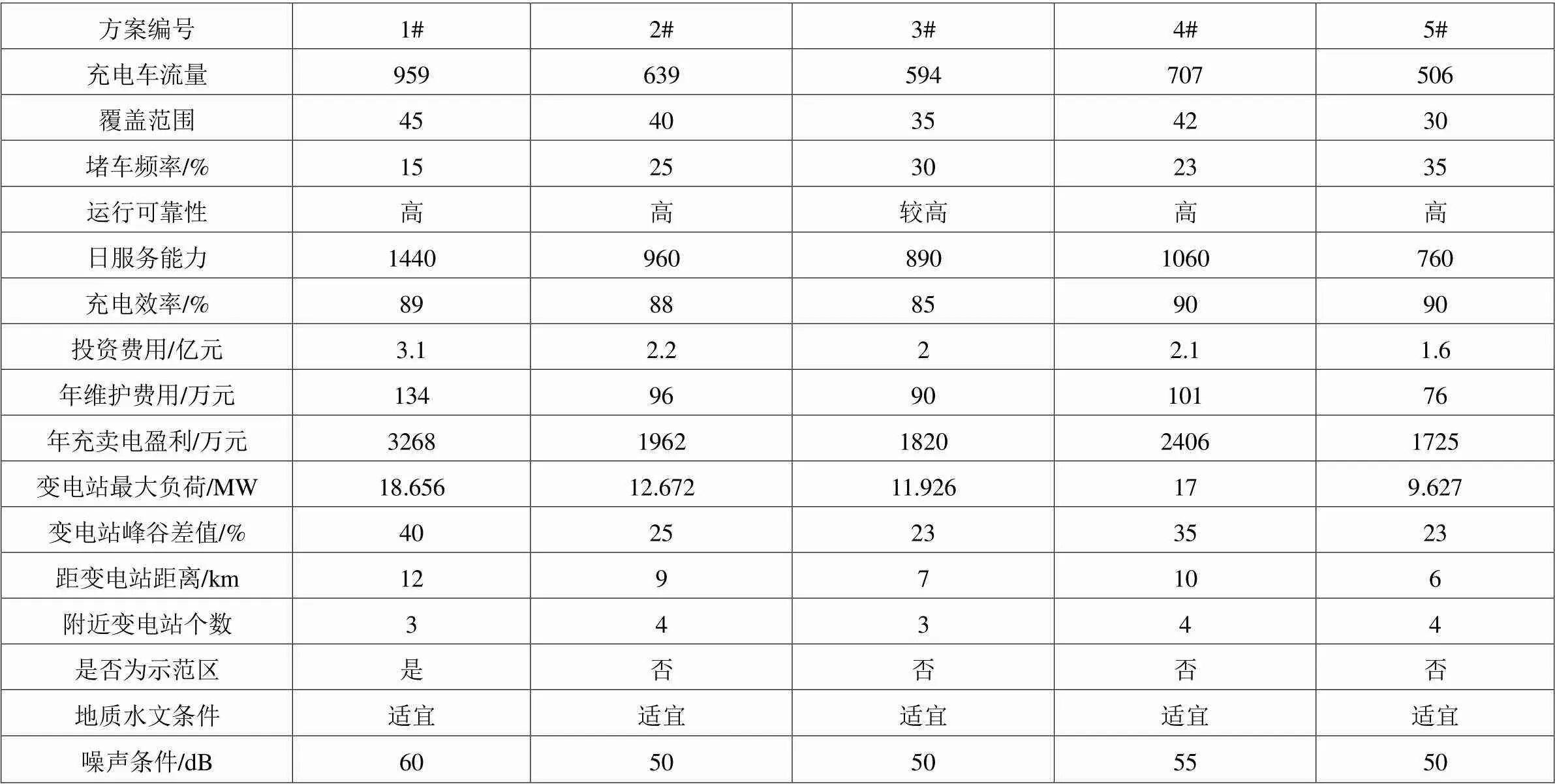
表2 某市充电站备选方案数据

表3专家对某市5个充电站备选方案针的各个因素的量化评分

Table 3 Scores of five charging stations in the city from specialists

3.5 关联度处理

对应于寻找最佳加油站选址的模糊物元分析,求出关联度之后,需要对关联度进行比较,从而获得最符合要求的解。最常用的比较原则是最大关联度原则,从各个事物的关联度中找出最大值,即

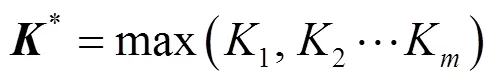
将矩阵(12)和表2中的数据代入式(14)可得

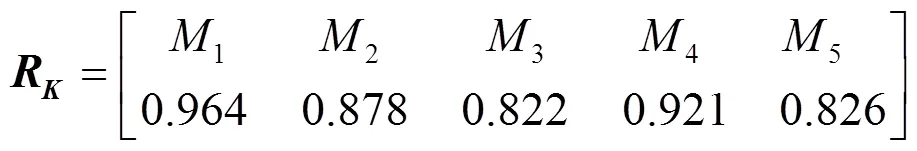
根据矩阵(17)中的数据，并根据模糊物元决策的最大关联度原则得出，一号备选方案应为最适合方案。为了验证得到的结果，采用传统的AHP与模糊物元方法验证结果得到如下的关联度矩阵[23]。

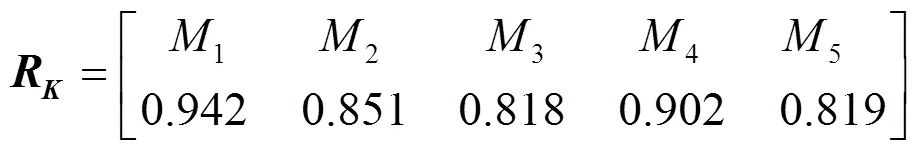
由式(18)可以看出，一号备选方案为最优方案，这与文中所得到的结果是一致的，证明了基于层次分析法与模糊物元分析的城市充电站选址决策方法的科学性和有效性。

4 结论

根据改进的AHP方法和模糊物元方法构建的电动汽车充电站选址评价方法，科学细致地分析了各个因素对电动汽车充电站选址评价的影响，利用改进的层次分析法构造出客观的选址模型，并且采用三级标度来确定比较矩阵，所需信息简单、直观，易于被专家与决策者接受与掌握。运用层次分析法与模糊物元分析相结合的方法对某市的电动汽车充电站选址进行评价与决策，所得到的结果与运用传统的选址模型得到的结果趋于一致，证明了这种方法的合理性和科学性，为城市充电站选址最优规划提出了简便、科学的实用性方法。

[1] 刘坚. 电动汽车充电方式和商业运营模式初探[J]. 汽车工程师, 2011, 1: 19-22.

LIU Jian. A preliminary study on charging infrastructure development and business operation models[J]. Auto Engineer, 2011, 1: 19-22.

[2] 高赐威, 吴茜. 电动汽车换电模式研究综述[J]. 电网技术, 2013, 37(4): 891-898.

GAO Ciwei, WU Xi. A Survey on battery-swapping mode of electric vehicles[J]. Power System Technology, 2013, 37(4): 891-898.

[3] 周利梅. 电动汽车充换电站选址规划布局研究[D]. 济南: 山东大学, 2012.

ZHOU Limei. Research on the location and plan of electric vehicle charging station[D]. Jinan: Shandong University, 2012.

[4] 冯超, 周步祥, 林楠, 等. Delphi和GAHP集成的综合评价方法在电动汽车充电站选址最优决策中的应用[J]. 电力自动化设备, 2012, 32(9): 25-29.

FENG Chao, ZHOU Buxiang, LIN Nan, et al. Application of comprehensive evaluation method integrating Delphi and GAHP in optimal siting of electric vehicle charging station[J]. Electric Power Automation Equipment, 2012, 32(9): 25-29.

[5] 雷琪, 苗世洪, 郭宝甫, 等. 基于层次分析和改进逼近理想解法的分层储能系统综合评估[J]. 电力系统保护与控制, 2017, V45(3): 13-19.

LEI Qi, MIAO Shihong, GUO Baofu, et al. Comprehensive evaluation of hierarchical storage system based on analytic hierarchy process and improved technique for order preference by similarity to ideal solution[J]. Power System Protection and Control, 2017, V45(3): 13-19.

[6] 张晶晶, 许修乐, 丁明, 等. 基于模糊层次分析法的变压器状态评估[J]. 电力系统保护与控制, 2017, V45(3): 75-81.

ZHANG Jingjing, XU Xiule, DING Ming, et al. A condition assessment method of power transformers based on fuzzy analytic hierarchy process[J]. Power System Protection and Control, 2017, V45(3): 75-81.

[7] 韩子娇, 李正文, 赵鹏, 等. 基于改进模糊AHP的电磁环网解环方案评估[J]. 电力系统保护与控制, 2016, V44(5): 95-101.

HAN Zijiao, LI Zhengwen, ZHAO Peng, et al. Scheme evaluation for decoupling electromagnetic loop networks based on improved fuzzy AHP[J]. Power System Protection and Control, 2016, V44(5): 95-101

[8] 张卫中, 陈从新, 张敬东. 改进的AHP及其在地灾易发程度分区中的实践[J]. 土木建筑与环境工程, 2009, 31(2): 85-89.

ZHANG Weizhong, CHEN Congxin, ZHANG Jingdong. Improved AHP assessment model and its practice in geological hazard susceptibility zoning[J]. Journal of Civil, Architectural & Environmental Engineering, 2009, 31(2): 85-89.

[9] 李光. 影响我国电动汽车产业发展的关键因素研究[D].武汉:武汉理工大学, 2011.

LI Guang. Research on the key factors influencing the development of electric vehicle industry in China[D]. Wu Han: Wuhan University of Technology, 2011.

[10] 袁加妍, 潘莹, 张娥. 电动汽车充(换)电站选址评价体系的构建[J]. 电力与能源, 2014, 35(3): 390-393.

YUAN Jiayan, PAN Ying, ZHANG E. To establish evaluation system for location selection of electric vehicle charging and swapping station[J]. Power & Energy, 2014, 35(3): 390-393.

[11] DM Kim, JO Kim. Design of emergency demand response program using analytic hierarchy process[J]. IEEE Transaction on Smart Grid, 2012, 3(3): 635-644.

[12] W Pedrycz, M Song. Analytic hierarchy process (AHP) in group decision making and its optimization with an allocation of information granularity[J]. IEEE Transaction on Fuzzy Systems, 2011, 19(3): 527-539.

[13] Y Zhang, H Zhang, Z Zhong, et al. Objectively evaluating environmental comprehensive quality by improved AHP method[C]// IEEE, The International Conference on Bioinformatics and Biomedical Engineering, May, 2008.

[14]严世华, 田效. 基于层次分析法的判断矩阵一致性调整方法[J]. 兵工自动化, 2008, 27(4): 6-10.

YAN Shihua, TIAN Xiao. Method of comparison matrix consistency adjustment based on AHP[J]. Armament Automation, 2008, 27(4): 6-10.

[15]徐健, 边信黔, 常宗虎. 基于改进层次分析法的AUV重规划决策问题的研究[J]. 哈尔滨工程大学学报, 2007, 28(4): 28-32.

XU Jian, BIAN Xinqian, CHANG Zonghu. Optimizing replanning decisions for autonomous underwater vehicles through an improved analytical hierarchy process[J]. Journal of Harbin Engineering University, 2007, 28(4): 28-32.

[16] LI Zhan, SG Zhou, K Wang. A method for constructing perfectly consistent judgment matrix in AHP [J]. Journal of Zhengzhou University, 2008, 40(1): 10-14.

[17] L Yun, X Rui, B He, et al. Transfer matrix method for a two dimensional system[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(5): 712-720.

[18] 王广月. 基于改进的AHP方法进行地基处理方案的优选[J]. 水文地质工程地质, 2003, 5: 98-101.

WANG Guangyue. Improved AHP method for optimization of foundation treatment scheme[J]. Hydrogeology and Engineering Geology, 2003, 5: 98-101.

[19] 于强强. 基于行为的电动汽车充换电需求与服务容量的研究[D]. 济南: 山东大学, 2014.

YU Qiangqiang. The study of demand for electric vehicles and capability of services based on behavior[D]. Jinan: Shandong University, 2014.

[20]谢季坚, 刘承平. 模糊数学方法及其应用[M]. 武汉: 华中科技大学出版社, 2000.

XIE Jijian, LIU Chengping. Fuzzy mathematics method and its application[M]. Wuhan: Huazhong University of Science and Technology Press, 2000.

[21]张斌. 模糊物元分析[M]. 北京：石油工业出版社, 1997.

ZHANG Bin. The fuzzy matter-element analysis[M]. Beijing: Petroleum industry press, 1997.

[22] 王德荣, 王智源，李必鑫. 基于模糊物元分析的城市加油站选址决策方法研究[J]. 重庆科技学院学报(自然科学版), 2008, 10(3): 121-125.

WANG Derong, WANG Zhiyuan, LI Bi-xin. Study on method based on fuzzy-matter element analysis for location selection decision of service station in cities[J]. Journal of Chongqing University of Science and Technology (Natural Science Edition), 2008, 10(3): 121-125.

[23] H Luo, J Ruan, F Li. A fuzzy evaluation and AHP based method for the energy efficiency evaluation of EV charging station[J]. Journal of Computers, 2014, 9(5): 1185-1192.

Method Based on AHP and Fuzzy Matter-element to Solve Location Decision of Electric Ve-hicle Charging Station

WANG Zhe1, YIN Shuaibing1,WANG Junsheng1,ZHOU Jiyao2

(1. XJ Electric Co.,ltd, Henan Province，Xuchang 461000, China; 2. Hebei University of Technology, Tianjin 300401, China)

In order to improve the scientificity of electric vehicle charging station selecting in the city, and improve efficiency of city power operation and urban traffic operating conditions. AHP method combined with fuzzy matter-element analysis method are applied to the comprehensive decision on site selection of electric vehicle charging stations in the city. Translate the influence of related factors on electric vehicle charging station into weight function by AHP method. And build multi-dimensional complex fuzzy matter-element matrix of several location options by fuzzy matter-element method. The incompatible problem is transformed into a compatible problem through the associated transformation. So provide quantitative analysis for the several electric vehicle charging station alternatives and provide data support for electric vehicle charging station optimization. It shows that the results are obtained by using the method of AHP and fuzzy matter-element analysis are the same as traditional location selection model. The results verify the rationality and scientificity of the method, and provide a scientific and practical method for electric vehicle charging station selection in the city.

AHP method; fuzzy matter-element analysis method; electric vehicle; charging station; optimization

2017-08-11；

2017-09-30

王 哲(1990-)，男，硕士，助理工程师，研究方向为电力系统继电保护及电动汽车充换电产品的研发测试；E-mail: 790015244@qq.com

殷帅兵(1989-)，男，硕士，助理工程师，研究方向为电动汽车充换电系统、汽车链高速特性；E-mail: yinsb2016jlu@163.com

王军生(1963-)，男，本科，高级工程师，研究方向为电力系统产品设计与制造工艺及应用。E-mail: 553173754@ qq.com

工业和信息化部2015年智能制造专项一电力系统测控设备智能工厂标准化试验验证系统[2015—40]