True-Load 载荷反求算法研究与应用

李晓峰, 刘海东, 冯建军, Timothy G. Hunter

(1. 大连交通大学 交通运输工程学院，辽宁 大连 116028；2.Wolf Star Technologies,LLCMilwaukee,WI 53211)

0　引言

随着轨道车辆特别是高速动车组、快捷货车等干线运营车辆迅速发展，车辆设计、制造对车辆设计载荷提出了越来越高的要求.在车辆产品早期设计阶段由于无法获得车辆在实际运行中的载荷，因此只能依据相关标准开展设计工作，然而这些基础性的标准往往是基于经验而形成的对具体的产品设计、试验、考核、可靠性等方面的规定不够完善[1].如果产品设计要求载荷高于实际运营载荷将对产品造成不必要的成本浪费，如果产品设计要求载荷低于实际运营载荷，将对产品运营中的可靠性造成潜在的影响，设置造成运营安全事故[2].所以如何能准确、有效地获得车辆运行载荷是国内外每一个设计和研究人员的目标，只有准确掌握真实载荷输入才能设计出满足实际工程需要的考核的产品[3].多年来对于获得车辆运行载荷的主要方法是利用车辆上嵌入特制的力传感器直接获取所需载荷，但这种方法对传感器自身质量、体积、结构、制作工艺有很高的要求，其次也可以测得易变形部位的变形量(如应变)实现测量并计算出作用载荷.但这种方法也存在安装繁琐、使用寿命短、测试成本高等缺点[4-5].True-Load算法提供了一种与有限元计算相结合的很好的载荷反求方法.

本文以该载荷反求算法为工具，在一致结构响应情况下分析对比通过载荷反求算法求解振动试验中高速列车外在天线基座的真实加速度，为这种算法的研究、推广提供参考依据.

1　基本算法简介

1.1　计算应变模态

假设系统为无阻尼振动，物理坐标系下结构动力学用方程描述为：

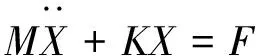
(1)

求方程(1)对应各阶模态向量Φ∈Rn×nq组成模态矩阵记为Φ=[φ1φ2φ3…φn]，模态叠加法坐标变换:

{x(t)}=[Φ]{q(t)}

(2)

其中,[Φ]为正则模态矩阵，对式(2)求导得到:

{ε(t)}=[ψε]{q(t)}

(3)

式中,[ψε]为模态应变矩阵.

1.2　确定应变片的最优位置及方向

通过对建立精确的有限元模型计算得到模态应变矩阵够构造矩阵[ψε]T[ψε]并依据D-Optimal算法遵循对应的行列式值最大的原则确定应变片的最优位置与方向[6].

1.3　实测应变信息并反求载荷

在最优贴片位置布置应变片，并获取相应的应变场数据，通过下式计算MPF:

(4)

返回到物理坐标系计算x(t):

(5)

返回系统动力学方程(1)通过下运用传递函数求得系统外载荷：

(ϖ)][F]

(6)

[M][a]=[F]

(7)

式中,α(ϖ)也称之为位移频响函数(DFRF).

2　天线基座载荷反求试验

下面以软件True-Load提供的载荷反求算法为工具，以高速动车组天线基座为研究对象进行载荷反求试验研究，以加深对该算法的进一步理解.

2.1　天线基座有限元模型建立

首先建立天线基座的有限元模型.基座由一块折弯平板、四根筋板组成，模型构成以壳单元网格划分为主，基座四周用于振动试验的四个质量块在有限元模型中以实体单元划分为主，与基座采用刚性单元连接.图1给出了天线基座的有限元模型，并给出了相应的约束.

图1　天线基座有限元模型

2.2　正向载荷及其约束

依据实际试验情况，在天线基座立板两侧共八个螺栓安装孔处约束6个自由度，整体模型X，Y，Z三个方向分别施加10 G单位加速度[7].此外在四个质量块与基座连接处分别在X，Y，Z三个方向施加1 000 N的单位预紧力，同时为了验证反求载荷需要，在试验过程在基座平板上布置了单向加速度传感器测试该处Z方向(即垂向)加速度值[8].

图2　天线基座有限元模型加载位置示意图

2.3　应变片群的布置

选取易于贴片部位的单元，在软件中设置单元筛选条件，并评估所选单元形成的[ψε]T[ψε]矩阵相关性，实现最优贴片.

试验选择的应变片群包括24个应变片，其位置如图3、图4所示.

图3　计算优化最佳贴片位置

图4　应变片群布置示意图

2.4　反求载荷数据及对比

通过模态迭加法计算正则模态并基于几何方程计算模态应变矩阵，由模态应变矩阵构造信息矩阵，使用D-Optimal准则确定最优的应变片的具体位置使用实测应变(计算应变均是主应变，它涵盖了应变的大小与方向信息)，从而求得结构实际载荷.

通过在天线基座上布置加速度传感器将测得的加速值与利用应变片测得数据反求出加速度值的载荷反求算法的计算值进行比较，图5给出了加速度测量值与计算值的对比.图中横坐标为时间坐标，纵坐标为加速度值，曲线2为将反求动态载荷加载在有限元模型上计算所得加速度，曲线1为实测加速度值大小.同时，为了进一步验证该算法，通过对加速度传感器布置点的动应变变化与施加了反求载荷的模型动应变变化进行比较如图6，图中横坐标为时间变化，纵坐标为动应变值，曲线1幅值较大为实测动应变，曲线2为反求载荷的模型动应变变化.

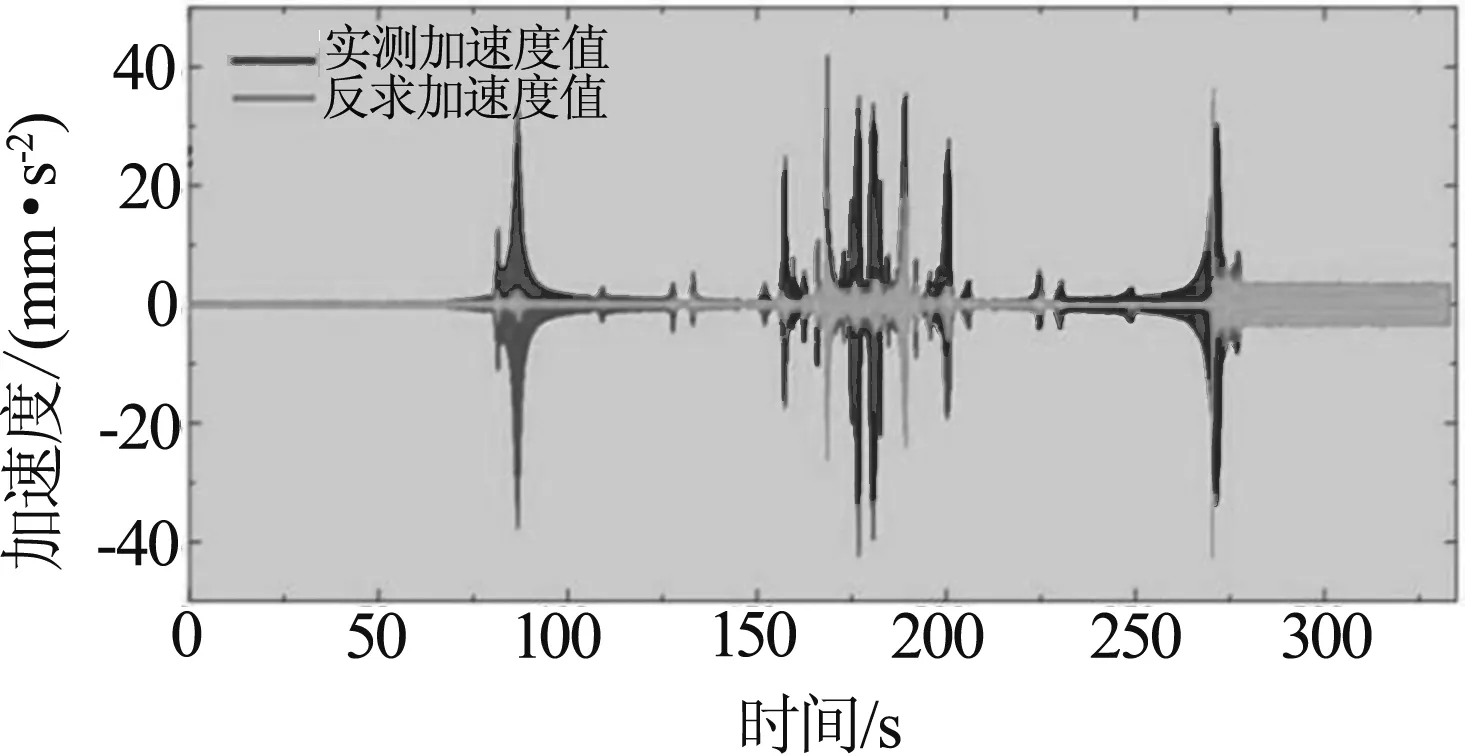
图5　第一测试点反求加速度与实测加速度对比

图6　第一测试点反求动应变与真实动应变对比

对比分析反求载荷值与实测相关数据可发现：

(1)反求载荷值与实测值变化趋势一致，但数值大小存在一定差异；

(2)贴片测量容易受到载荷变化幅值影响(图中在加速度变化较大点附近应变片测量值受到扰动).

3　结构优化设计

运用反求出的结构动态载荷，比对轻量化设计前后应力云图(图7)可以发现，两个角板的中心区域应力较小，分析可以对此结构处进行轻量化设计，且不影响整体基座的应力分布.

通过比对轻量化设计前后疲劳寿命图(图8)发现，其结构寿命满足要求，所求动载荷具有一定的可靠性及运用意义.

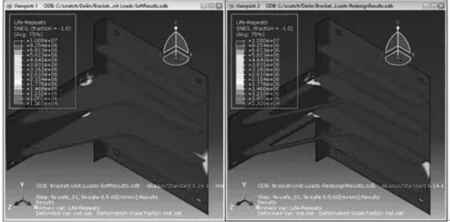
图7　轻量化设计前后结构应力云图对比

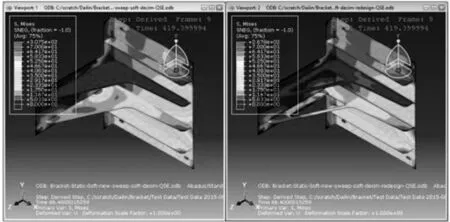
图8　轻量化设计前后结构寿命图对比

4　结论

论文以高速列车天线基座为研究对象，基于软件True-Load的算法进行了载荷反求研究，并以反求载荷为计算载荷，对原结构进行优化设计，在结构疲劳寿命不变前提下，减小了结构最大应力及结构质量.获得了很好的优化结构.但研究过程中也发现:

(1)建模的精度必须足够高；

(2)一旦初始应变实测数据不理想，载荷反求的误差将难以控制.

数据采集和应变片位置有很大联系，采用D-Optimal (行列式值最大化)算法本质只是数学明确的物理背景问题越复杂，越难保证初选的应变片贴片位置合理性[9].

参考文献：

[1]朱涛. 高速列车载荷反演技术及其运用研究[D].成都：西南交通大学,2012.

[2]毛玉明,林剑锋,刘靖华,等. 动载荷反演分析技术研究综述[J]. 动力学与控制学报,2014(2):97-104.

[3]朱涛,肖守讷,阳光武. 载荷识别研究进展及其运用于铁道轮-轨载荷研究概述[J]. 铁道学报,2011(10):29-36.

[4] 樊沿春.传感器技术及应用 [M]. 2版, 北京：北京航空航天大学出版社，2010.

[5]朱宁.200km/h客运机车转向架构架结构载荷系标定方案研究[D].北京：北京交通大学,2008.

[6]FU LI, ZHU YONGQUAN, WANG LINGLING, et al. A D-optimal Multi-position Calibration Method for Dynamically Tuned Gyroscopes[J]. Chinese Journal of Aeronautics,2011(2):210-218.

[7]王勖成，邵敏．有限单元法基本理论和数值方法[M]．北京：清华大学出版社，1997.

[8]RAO S S. 6.3 Influence Coefficients：Mechanical Vibration[M]. Upper Saddle River, NJ:Pearsion Hall, 2004: 455-57.

[9]KWAK. JIN HO, SUNGPYO HONG. Linear Algebra[M]. Boston: Birkhauserl, 1997.