黄土地基浸碱膨胀模型
朱 宏
(甘肃土木工程科学研究院,兰州 730020)
1 浸碱膨胀概念
浸碱黄土由于碱结晶及其生成物(包括生成的固体大结晶水化物)的增多,土孔隙体积随着时间增长而不断扩大,从而使黄土地基产生膨胀变形,这个过程称为黄土的浸碱膨胀[1-12]。
2 基本前提
在侧限条件下,设土样的初始高度为H0,浸碱过程中土样完全被饱和,膨胀后土样高度为H,则H=H0+S,S为膨胀力p作用下土样膨胀稳定后的变形量,假设土粒在浸碱过程中体积Vs不变,且设膨胀前初始孔隙比为e0,膨胀稳定后孔隙比为e。为求膨胀稳定后的孔隙比e,利用膨胀前后土粒体积和土样横截面面积不变的条件,得出

即
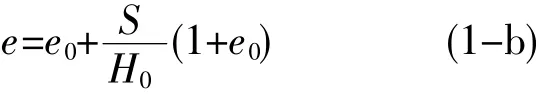
其中ds、ω0和γ0分别为土粒比重、土样的初始碱液含量(即土中碱液与水含量之和)和初始重度,这样,只要测得土样在膨胀力p作用下的稳定膨胀量S,就可按式(1-b)算出相应的孔隙比e,从而绘制出土样的膨胀曲线。
膨胀性不同的土,其e-p曲线的形状不同(图1),曲线上升愈快愈陡,说明随着膨胀力的增加,土孔隙比的增加愈显著,因而土的膨胀性愈大,所以,可用曲线上任一点的切线斜率a的大小来反映土的膨胀性大小。为此可将a定义为相应膨胀力p作用下的膨胀系数,即:


图1 土的e-p膨胀曲线
图1表示随着膨胀力p的增加,e逐渐增大,设膨胀力由 p1增至 p2,假定 p1、p2在 100~200kPa之间变化,相应的孔隙比由e1增至e2,则与膨胀应力增量Δp=p2-p1对应的孔隙比的变化量为Δe=e2-e1,此时,土的膨胀性可用图2割线M1M2的斜率近似表示。
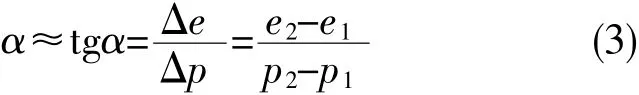
设割线与横坐标轴的夹角为α,则式中α为土的膨胀系数,p1为地基某深度处土中竖向膨胀应力,p2为同一深度处延续一段时间后土中的膨胀应力,e1相应于p1作用下膨胀稳定后的孔隙比,e2相应于p2作用下膨胀稳定后的孔隙比。

图2 以e-p膨胀曲线确定膨胀系数α
3 饱和土的浸碱膨胀
一般认为当土中孔隙体积的80%以上为液体填充时,土中虽有少量气体存在,但大部分是封闭气体,就可视为饱和土。
参照饱和土的渗透固结理论,可借助弹簧活塞模型来研究黄土地基浸碱膨胀规律,如图3所示由土骨架与土中碱液分担应力变化的简单模型可知,饱和土上的膨胀力初始时全部由土中碱液承担,随着时间的增加和碱液的不断渗入,膨胀产生,膨胀力逐渐转嫁给土骨架,直到全部由土骨架承担为止。
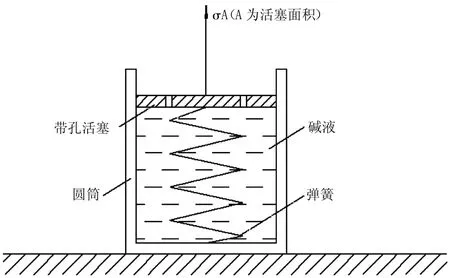
图3 土骨架与土中碱液分担应力变化的简单模型
在饱和膨胀过程中,一定压力下的膨胀应力σ总是等于有效应力σ'与孔隙碱液压力之和,由于孔隙碱液压力为负孔压;土骨架受拉,有效应力σ'为负,所以有

由上式可知,在膨胀的一瞬间,由于-u=σ,所以σ'=0;而当膨胀变形完全稳定时,则-σ'=σ,μ=0。因此,只要土在孔隙碱液压力还存在,就意味着土的浸碱膨胀尚未完成。
4 一维膨胀模型的建立
仿照K.Terzaghi关于一维(压缩)固结的理论方法[13-18],可在不同情况下得出相应于浸碱膨胀的一组公式和满足碱液应力的偏微分方程:假设土体孔隙中碱液主要沿竖向渗流,现考虑一维膨胀情形,设厚度为H的浸碱黄土层的顶面是透液的,而其底面是不透液的;又设土层在自重及顶面荷载p0的作用下,由碱液引起了土层的膨胀;并假设。
1)土是均质、各向同性的和完全被碱液饱和的。
2)土粒和孔隙中的碱液是不可压缩的,只有土的颗粒骨架可变形,膨胀系数α为常数。
3)荷载沿水平面是均匀无限分布的,而且是一次性加荷的,因此土层的膨胀和碱液的渗流都是唯一的。
4)土中碱液的渗流服从达西定律,V=K·i;其中k为渗透系数,i为渗透梯度。
在膨胀土层顶面z深度处的一个微元体(见图4),由于饱和固结渗流是自上而下,在附加荷载下某时刻t流入和流出微单元体的碱液q'和q"分别为
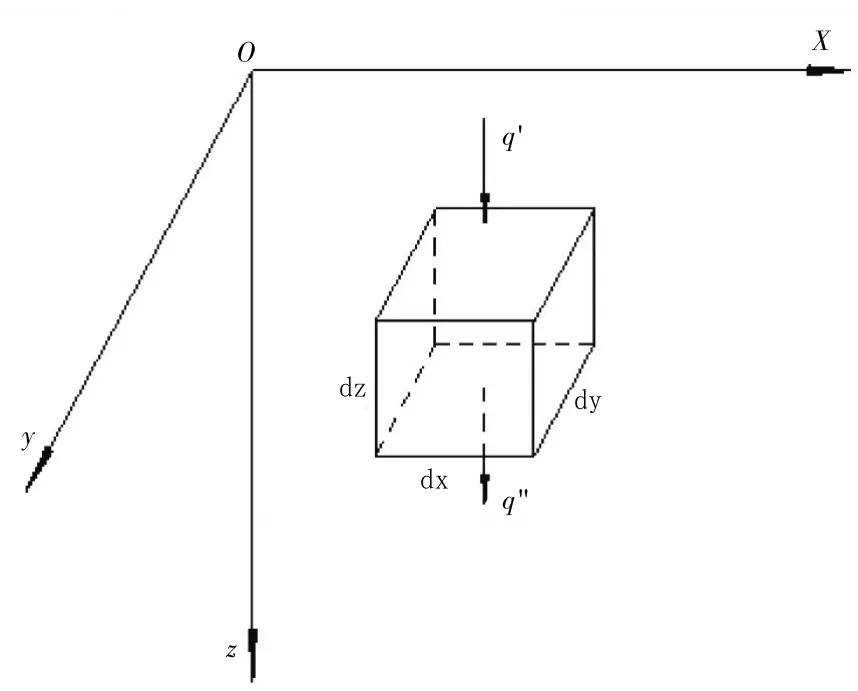
图4 微元体示意图

式中k——z方向的渗透系数,cm/s(1cm/s≈3×107年);
i——渗透梯度;
h——渗透面下z深度处的超静液压头cm;
A——为微元体的过液面积,cm2;A=dxdy。
其中(5-b)是个近似等式,它是借助拉格朗日微分方程中值公式得到的,
即 f(z+dz)-f(z)=f'(z+θdz)dz,0<θ<1
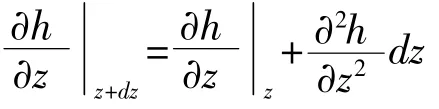
于是,在时刻t,在单位时间(dt=1)内微元体的液量变化为
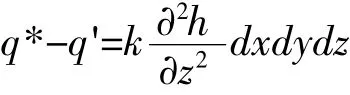
已知微元体中孔隙体积的膨胀率(增加)为
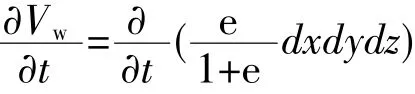
式中e为土的天然孔隙比。
根据膨胀渗流的连续条件,微元体在某时刻t,在单位时间(dt=1)内的碱液量变化等于同一时刻t,在单位时间内该微元体中孔隙体积和膨胀量的变化,即

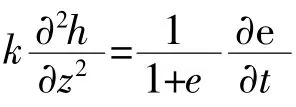
由土的应力——应变关系的侧限条件,(2)式有:
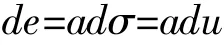
或



上式即浸碱黄土的一维膨胀偏微分方程,其中Cv称为土的竖向膨胀变形系数,它与竖向压缩固结系数不同的是,Cv计算式中a为膨胀系数,如(2)或(3)式所示。
5 模型方程的解
5.1 讨论模型方程所满足的初始条件和边界条件
当t=0和0≤z≤H时,u=σ,这相应于起始时刻浸碱土尚未膨胀且无生成物结晶时,膨胀应力全部由饱和土的碱液压力承担;
0<t<∞和z=0时,相应于顶层表面的碱液压力为零;
t=∞和0≤z≤H时,u=0,这时浸碱土达到稳定膨胀,土中孔隙的碱液压力已减为零。
在上述初始条件及边界条件下求方程(10)解的问题,称为膨胀模型方程(10)抛物型方程的混合问题。
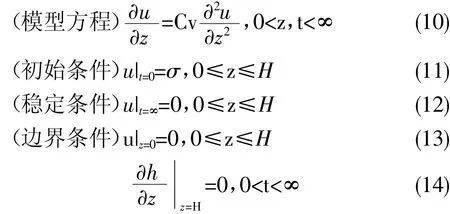
5.2 抛物型方程混合问题的解
下面利用富氏级数,以分离变量法对抛物型方程混合问题(10)求解。设方程(10)的通解形式为
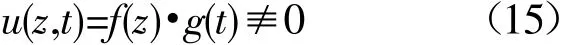
将(15)代入(10),有
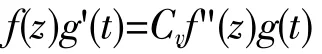
即
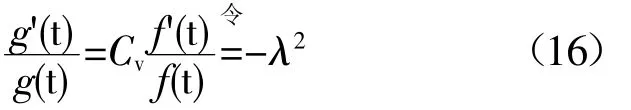
式中的λ与t和z无关,为常数,由(16)的第二等式,得

解上述微分方程,得通解
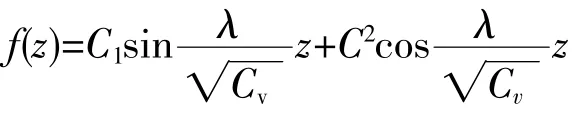
由边界条件(13),得C2=0,所以通解为
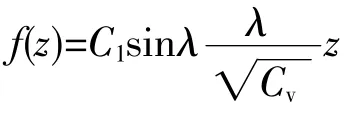
由上式得
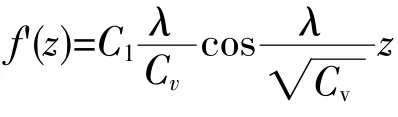
利用边界条件(14),由 C1≠0 得
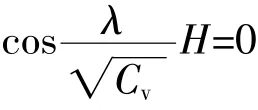
即
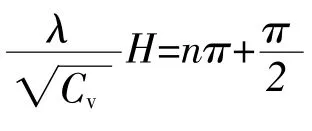
亦即
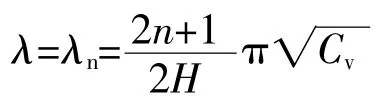
其中,n=0,1,2,…
于是得(17)的解为
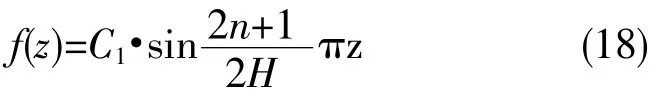
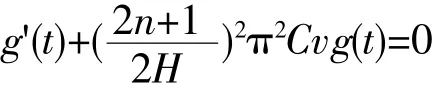
解得
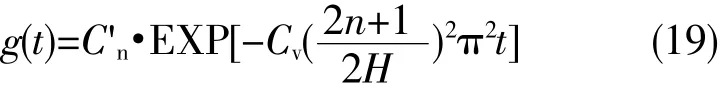
(19)式中的 C'n为常数。把(18)和(19)代入(15),并让n从0到∞迭加,再令C1·C'n=Cn,可得方程(10)满足边界条件(13)和(14)的解

利用初始条件(11),有
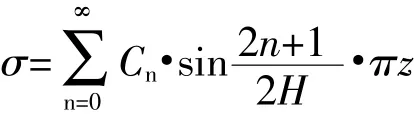
为了确定Cn两边乘以,并从0到关于z的积分,其中,求得
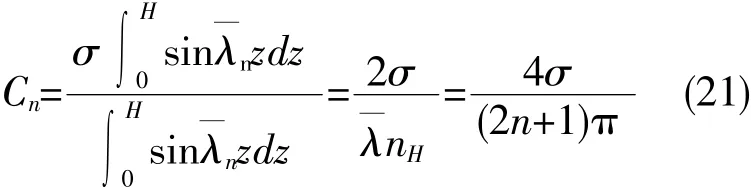
将(21)式中的Cn代入(20),便求出抛物型方程混合问题(10)~(14)的解为

由此看出,(22)中的解u也适合t→∞时的稳定条件(12),表达式(22)是混合问题(10)~(14)的唯一解。
当n增大时,由于(22)式中含有急降的指数因子,因此级数(22)收敛很快,通常可取其中第一项作为u的近似值,即在(22)中取n=0,可得
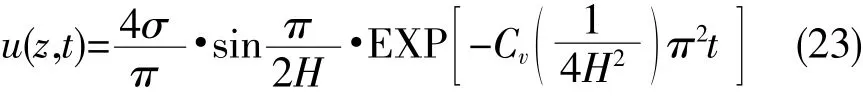
(23)式便是混合问题(10)~(14)的近似解析解。
由解得表达式(22)或(23)看出,当时间 t增加时,由于u含急降因子,u的值将随时间减少,并随t→∞而趋于零;又因为在膨胀发展过程中,土的膨胀应力不会减少,由(4)式

看出,这时有效应力σ'将随u的减小而逐渐增至σ,这与膨胀过程的实际相符。
为了进一步应用,现考虑土在完全侧限条件下的竖向膨胀应力与相应的变增量之比值,设a为土的膨胀系数,e0为相应于p0作用下膨胀稳定后的孔隙比,则称比值

为膨胀土的膨胀模量。
在内部膨胀力的作用和侧限条件下,土层的最终膨升量 S,由(1-a)式,解得
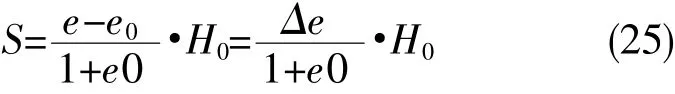
又由(3)式得膨胀系数

式中σ为一定压力下的膨升应力,由此得

将(26)式中的?e代入(25)式,并应用关系式(24),得
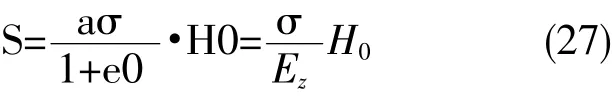
公式(27)可用于计算膨胀土层的最终膨升量S。
有了孔隙碱液压力u随时间t和深度z变化的函数关系式(22)或(23),便可求得地层在任一时刻的膨升量,为此,需用到地基的膨胀度U,即
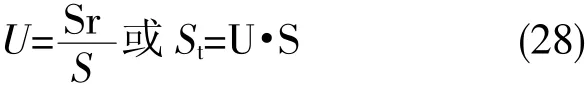
式中的St为地基在t时刻的膨升量,S为地基的最终膨升量。
地基土膨胀时,又(4)式知
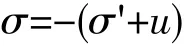
在某一压力下的膨升力为:

在竖向膨胀情况下,膨升量St与膨胀应力σ成正比;最终膨升量S与P成正比,由图5看出,由于σ'值随z变化,为了确定U,就用σ'在区间[0,H]上的积分平均值,来替代(28)中的St,于是
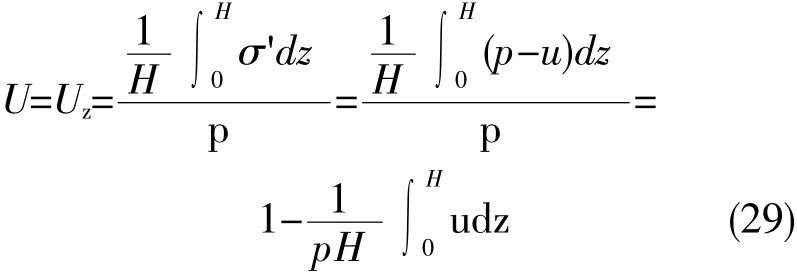
式中的Uz称为竖向平均膨胀度,u=u(z,t)为时刻t,深度z处的孔隙碱液应力,p为土层在一定均布荷载下的膨胀力。
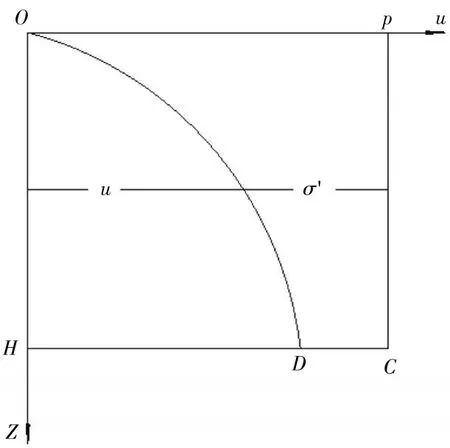
图5 一维膨胀情况

将(30)代入(29)式右端,取σ=p得到
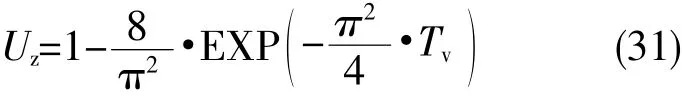
利用函数关系,可绘出图6中的Uz-Tv关系曲线,便于在图中求某Tv时间对应的Uz值,反之亦然。
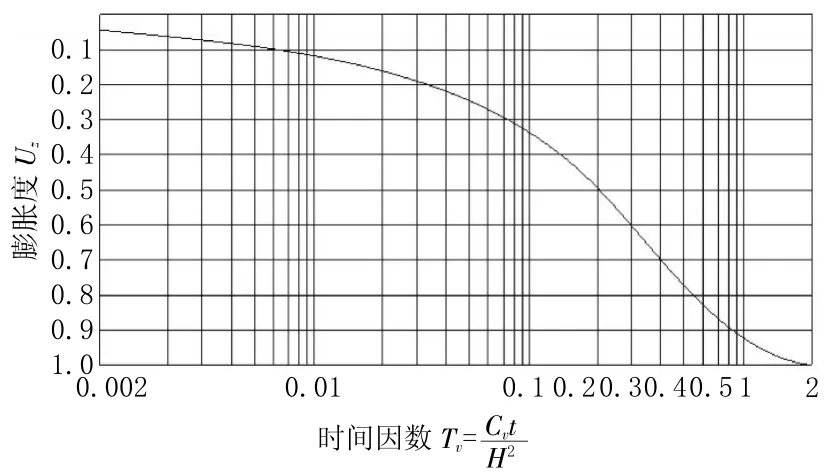
图6 膨胀度Uz与时间因数Tv的关系曲线
6 两个重要方程得建立
下面由前面的基本公式来推导瞬时膨升力pt与时间的函数关系,以及最终膨升量S与最终膨升力p的表达式。
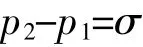
视p2=ptp1=p0(初始膨升力)
由(27)得
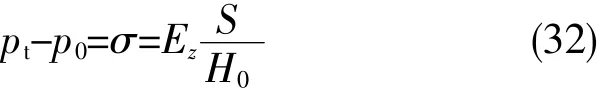
再利用(28),并认为t=0时,p0=0(尚未膨胀,膨升力为零),于是得出瞬时膨升力pt为

其中


令 t→∞,由于 Uz→1,St→S,由(33)式,得到(34)表示最终膨升p力与土层的相对膨升量成正比,其比例系数正好为土层的膨胀模量Ez。由此看出(34)式与弹性力学中著名的Hooke定律极其相似。
当最终膨升量S不变时,厚度H0越大,表明相对膨升量越小,所以最终膨升力p这时也越小,这表明最终膨升力p与H0成反比;同样,当H0固定时,(34)式表示p与S成正比,即瞬时膨升力p与相对膨升量成正比,其比例系数即为Ez。
7 应用举例
例题1 某饱和浸碱土层的厚度为1m,在大面积荷载p0作用下,设该土层的初始孔隙比e0=1,膨胀系数a=1MPa-1,膨胀模量Ez=6MPa,渗透系数k=0.75cm/年,对黄土层在单面浸碱条件下,已知p0荷载下膨胀力为120kPa。
求:(1)加荷半年时的膨升量;
(2)膨升量达10mm时所需的时间。
解:(1)求t=0.5年时的膨升量:

由公式(27)可求得黄土层的最终膨升量
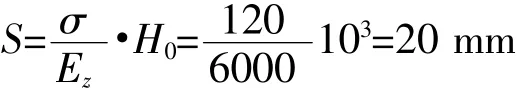
黄土层的竖向膨胀变形系数
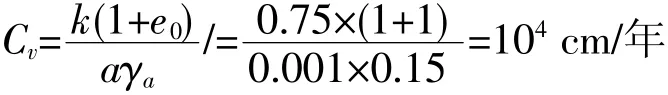
在单面浸碱条件下,竖向膨胀时间因数

由图6中的Uz-Tv曲线查得相应的膨胀度Uz=0.78,由(28)式,则得出t=0.5年时浸碱土的膨升量St=Uz·S=0.78×20=15.6mm
(2)求膨升量达10mm时所需的时间:
由图6中的Uz-Tv曲线查得相应的时间因数Tv=0.2;在单面浸碱的情况下,求得膨升量达10 mm所需的时间
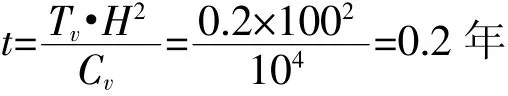
即为2.4月
该计算结果与现场实测值基本相符;
例题2 某饱和浸碱土层的厚度为1m,膨胀模量Ez=60MPa,浸碱120天,最终膨升量为4mm,求其最终膨升力pmax为多大?
解:由(34)式,知

则
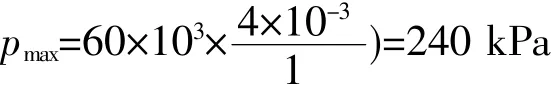
该计算结果与现场荷载试验实测值基本相符。
8 结语
本文通过用土力学中Terzaghi一维固结理论的方法,研究黄土地基浸碱膨胀变形规律,建立了黄土地基浸碱膨胀的数学模型,从而推导出膨胀变形与时间的关系方程,此外还建立了膨胀力与膨胀变形的关系表达式: 此式与弹性力学中著名的Hooke定律极其相似。此方法对地基浸碱膨胀的事故的处理,有一定的理论价值。
参考文献:
[1]郑世益.耐碱砼及地坪构造的研究[R].兰州:兰州有色金属建筑研究院,1995.
[2]廖修胜.黄土地基浸碱膨胀变形的研究[R].兰州:兰州有色金属建筑研究院,1993.
[3]YBJ-89,钢铁工业建(构)筑物可靠性鉴定规程[S].
[4]朱宏.山西铝厂三蒸发车间沉降开裂事故调查报告[R].兰州:兰州有色金属建筑研究院,1996.
[5]GBJ112-89,膨胀土地区建筑技术规范[S].
[6]梁俊勋.用灰色聚类法评判膨胀土胀缩等级的初步尝试[R].南宁:南宁市勘测院,1992.
[7]翟礼生.中国膨胀土地基承载力的选用[R].北京:中国建筑科学研究院地基所,1988.
[8]轻工业部上海轻工业设计院勘测室土建室技术组.土受碱液侵蚀后对强度影响的研究[R].1982.
[9]李宏义,刘洪平.碱液法加固新进堆积黄土地基的研究[R].石家庄:机电部北方勘察研究院,1990.
[10]李云章.湿陷性黄土地基碱液加固[J].建筑结构学报,1982(01).
[121]B.M.莫斯克文.混凝土和钢筋混凝土的腐蚀及其防护方法[M].北京:化学工业出版社,1984.
[13]T.Nilliam Lambe.,Robert V.Whitman.oil Mechanics[M].SI Version,1969.
[14]Terzaghi,K..Theoretical Soil Mechanics[M].New York:John wiley and Sons,1943.
[15]Terzaghi,K..From Theory to practicein Soil Mechanics[M].New York:John wiley and Sons,1960.
[16]Schiffman,R.L..Consolidation of soil under Time-Dependent Loading and Variable Permeability[J].Proc.Highway Research Board,1958(37).
[17]Schiffman,R.L.,A chen,and J.C.Jordan.The consolidation of a Half plane[R]U.ofIllinois(Chicagocicle)MATE Report,67-3,1967.
[18]Cryer,C.W.A Comparison of the Three-Dimensional Consolidations Theories of Biot and Terzaghi[J].Quarterly Journal of Mechanics and applied Mathmatics,1963(16).

