A modified multi-objective particle swarm optimization approach and its application to the design of a deep water composite riser
Y.Zheng·J.Chen
1 Introduction
Traditional multi-objective optimization problem(MOOP)methods attempt to find a set of non-dominated solutions using mathematical programming.The weighting method and theε-constraint method are the most commonly used techniques.Both methods transform an MOOP into a single objective problem,which can be solved using nonlinear optimization techniques.With the weighting method,nondominated solutions are obtained if all weights are positive.However,this method does not guarantee that all Pareto optimal solutions will be found.Another disadvantage of this method is its inefficiency,since numerous different sets of weights may produce the same solution.Theεconstraint method possesses similar drawbacks in dealing with MOOPs.
Evolutionary algorithms(EAs)are recommended candidates for MOOPs due to their ability to search simultaneously for multiple Pareto-optimal solutions,as well as their global search feature.Many types of EAs for multi-objective optimization have been proposed with varying degrees of success,such as the non-dominated sorting genetic algorithm II(NSGA-II)[1]and the strength Pareto evolutionary algorithm 2(SPEA2)[2].In addition,Kennedy and Eberhart[3]proposed a particle swarm optimization(PSO)algorithm.Because of its simplicity and fast convergence,PSO has been successfully applied to many single-objective optimization design problems.Works of Khalili-Damghani et al.[4]and Garg and Sharma[5]dealt with reliability redundancy allocation problems by using the multi-objective PSO(MOPSO)algorithm.Then,Zhang et al.[6]used a bare-bones MOPSO in solving an environmental/economic dispatch problem.One of the disadvant ages of MOPSO is its premature convergence.To overcome this,many researchers[7–9]suggested that the global best(gbest)solution should be chosen from the non-dominated solutions in the external archive in the current iteration.By limiting the case that the personal best(pbest)is far from gbest,Zhao and Suganthan[10]proposed a two-local best(lbest)based MOPSO to reduce the inefficient motion of a particle.On the other hand,several effective particle updating strategies are incorporated into MOPSO to improve the diversity of the Pareto-optimal solutions,such as the hyper-grid approach[9]and the Sigma method[11].
In many engineering optimization problems,objective functions or constraint functions are computationally expensive or implicit.Surrogate models are employed to fit these functions.Polynomial regression,Kriging meta-model,radial basis function(RBF)interpolation,neural networks,and support vector regression are commonly used.Numerous surrogate-based strategies are proposed to solve problems involving engineering design,e.g.,surrogate models are combined with EAs.Most implementations use surrogates only for single objective function problems.Only a few researchers have used surrogate models for multiple constraint functions[12],for multiple objectives[13–15],or introduce surrogate models to approximate simultaneously the objective functions and constraint functions in a multiobjective problem[16,17].
The true solution of an MOOP is generally a hyper surface,such as a curve for a bi-objective optimization problem or a surface for a tri-objective optimization problem.The hypersurface reflects a compromise between objectives,and is termed as thePareto front.Pareto-optimal solutions obtained by EAs are non-dominated by each other.They approach the Pareto front during iteration,but are not always exactly in the hypersurface due to the approximation of EAs.
In this paper,Kriging meta-models and the trapezoid index are introduced and integrated with MOPSO,i.e.,a modified multi-objective particle swarm optimization(MMOPSO)method is proposed.Kriging meta-models are used to match objectives and constraints,while the trapezoid index is employed to measure whether or not Pareto-optimal solutions converge to the Pareto front.In Sect.2,the traditional MOPSO is described.In Sect.3,Kriging meta-models and the trapezoid index are combined into MOPSO.Four illustrative examples are given in Sect.4.The design of a deepwater composite riser is discussed in Sect.5.Conclusions are drawn in Sect.6.
2 Multi-objective particle swarm optimization approach
In the traditional PSO method,candidate solutions are represented by a number of particles.These particles are attracted by the global optimum position of the crowdgbestand the personalpbest i.In each step,the velocity and position of a particle will be updated by Eq.(1):
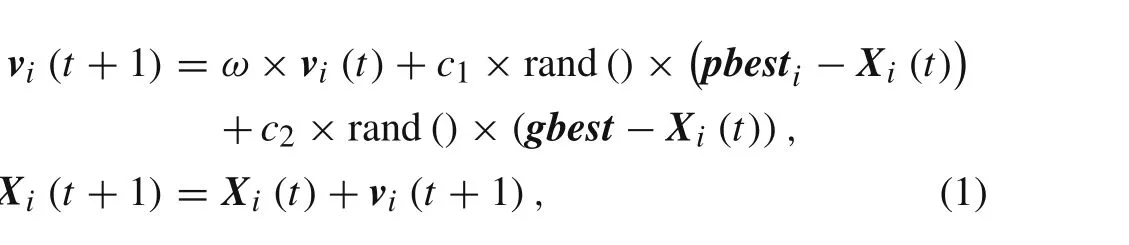
wherev i(t)andX i(t)are the velocity and position,respectively,of particleiat stept;ωis the inertia factor;c1andc2are acceleration coefficients;and rand()is a random number following a uniform distributionU(0,1).A maximum velocity valuevmaxis assigned forv i(t+1).As the iteration proceeds,all particles tend to move towardsgbestuntil the optimal is obtained.
In MOPSO,different updating rules are applied as compared to PSO,i.e.,pbest iandgbestare updated through a dominating principle.A solutionX(1)dominating another solutionX(2)means thatX(1)is not worse thanX(2)in all objectives,and strictly better thanX(2)for at least one of the objectives.So,three types of dominating cases exist:X(1)dominatesX(2),X(2)dominatesX(1),andX(1)andX(2)are non-dominated to each other.WhenX(1)andX(2)are non-dominated in a step of MOSPO,they should be saved and gathered in a set called anexternal archive.In the next step,gbest ifor particleiis selected randomly from the external archive.When updatingpbest i,ifX i(t+1)andpbest iare non-dominated to each other orpbest idominatesX i(t+1),pbest iwill be saved,otherwisepbest iis replaced byX i(t+1).
A nonnegative mutation parameterαmis used to control the probability of particle mutation.A particle will change its position randomly,when e−αmt/tmax>rand()at stept.The probability of mutation for a particle approaches zero as the iteration proceeds to the end.
A set of Pareto-optimal solutions can be obtained with the MOPSO mentioned above.These solutions are nondominated by any other solution in the whole search space.A decision-maker can select the required one from the Pareto optimal solutions according to his or her preference.In order to improve the computational efficiency of MOPSO,Kriging meta-models and the trapezoid index are introduced in the following sections.
3 A modified multi-objective particle swarm optimization approach
In MOPSO,particles evolve in each step and their fitness are evaluated.The Pareto-optimal solutions are obtained when the termination condition is reached.If an objective is an expensive or black-box function,great effort will be required to evaluate a particle.Even though only a small amount of time is needed when evaluating a particle,a large quantity of evaluations are necessary and much time will be spent on optimizing.Thus,decreasing the evaluation number constitutes a key issue in improving the computation efficiency.
In this section,Kriging meta-models and the trapezoid index are introduced into MOPSO in order to establish a convergence criterion and decrease the computational time.
3.1 Kriging meta-model
In recent years,surrogate models have been widely used in many fields.By using a small number of samples and their responses,a surrogate model can be built to match an expensive or black-box function.Through the surrogate model,the call number of the expensive or black-box function will be decreased and the computational efficiency will be improved.In this paper,the Kriging meta-model is used to match an expensive or black-box function.
The Kriging meta-model includes two parts,i.e.,the regression part and the correction part:

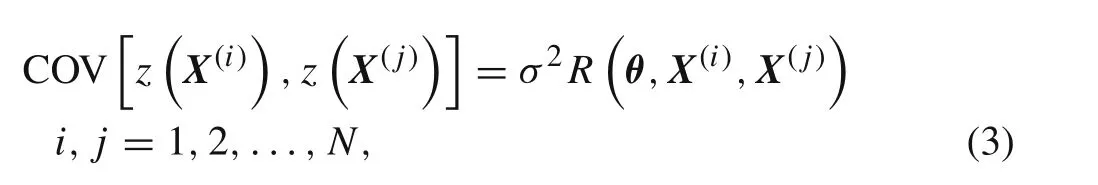
whereX(i)andX(j)are two of the samples;Nis the number of samples;andR?θ,X(i),X(j)?is a function about parameterθ,usually expressed as the type of Gaussian function:
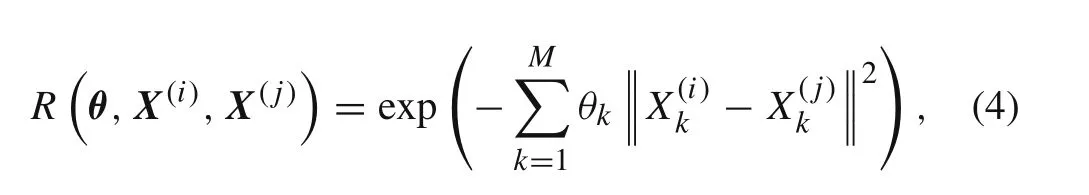
whereMis the dimensionality.
In a Kriging meta-model,the average of the predicted values’errors is required to be 0.Thus,θis determined by the maximum likelihood estimation:
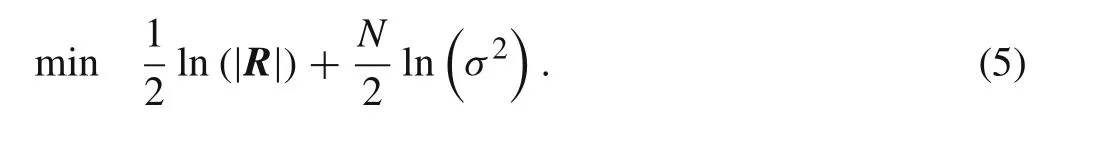
Through some manipulation,the black-box function’s predicted valueG?X∗?at pointX∗can be expressed as
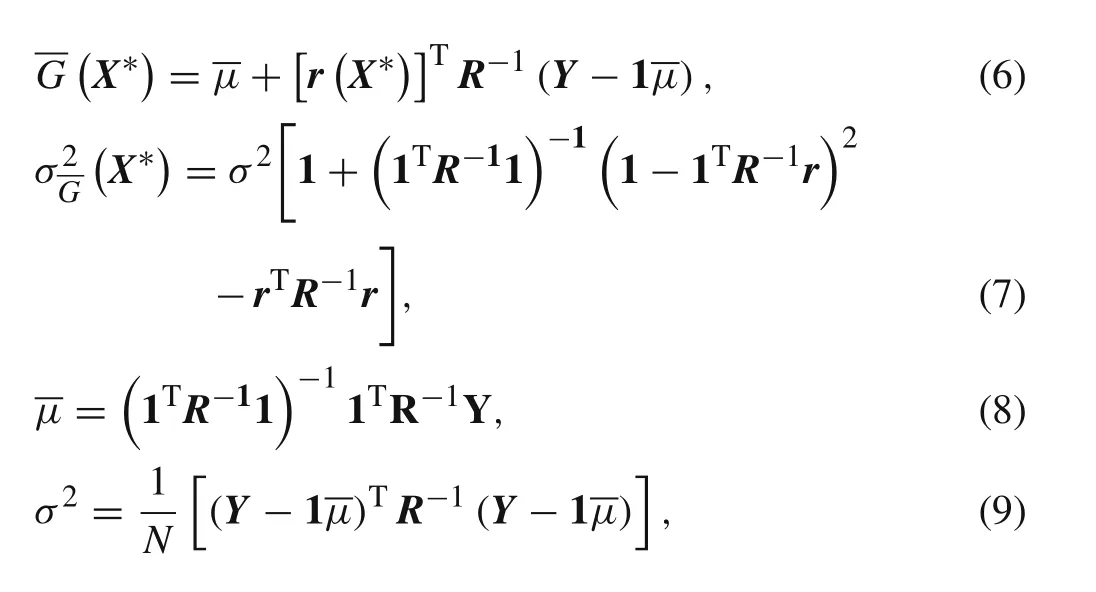
where 1 is a vector,which is composed by 1;Yis a vector of samples’function values;andr=r?X∗?is a vector of relative coefficientsRbetweenX∗and all sample points.
3.2 Trapezoid index
In a bi-objective optimization problem,for example,Paretooptimal solutions and the Pareto front can be shown in the objective space.Pareto-optimal solutions are obtained by some optimization method,while the Pareto front is regarded as th eactual curve,which is the optimal trade-off between the two objectives.Because of the approximation of EA,Paretooptimal solutions may not be on the Pareto front exactly.An ideal set of Pareto-optimal solutions are all on the Pareto front,and a diagram is shown in Fig.1.When every two neighbor Pareto-optimal solutions are linked,several trapezoids are formed between segments and one objective axis.The trapezoid index is defined as the sum of those trapezoids’areas.The trapezoid index measures how Pareto-optimal solutions converge to the Pareto front.After updating the Kriging meta-model by adding samples near the Pareto front,the precision of the Kriging meta-model is improved,and the trapezoid index of Pareto-optimal solutions obtained by MOPSO will approach the integral of the Pareto front to the objective axis.If the difference between the current trapezoid index and the previous one is small enough,the Kriging meta-model is regarded as being sufficiently precise,and the Pareto-optimal solutions converge to the Pareto front.
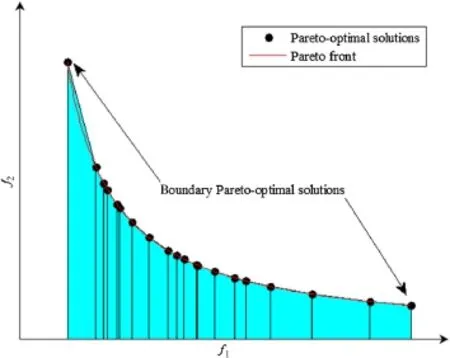
Fig.1 Trapezoid index
The trapezoid index of Pareto-optimal solutions is influenced by the boundary Pareto-optimal solutions(see Fig.1).If the boundary Pareto-optimal solutions change during the iteration,the trapezoid index will vary during the optimization process,even though the other Pareto-optimal solutions are unchanged.Since a boundary Pareto-optimal solution takes the minimal objective function value in a multiobjective optimization problem,the boundary Pareto-optimal solutions can be identified easily by optimizing each objective separately.Once the boundary Pareto-optimal solutions are achieved,the trapezoid index is calculated during the optimization process.A convergency criterion can be established based on the trapezoid index,i.e.,if the current trapezoid index differs from the previous one only slightly,the Paretooptimal solutions are considered to converge to the Pareto front,and the optimization completes in order to avoid redundant iterations and particles’evaluations.By combining the Kriging meta-model and the trapezoid index with MOPSO,a modified MOPSO methodology comes into being whose algorithm is described below.
3.3 The algorithm of M-MOPSO method
According to the discussion above,the flow of M-MOPSO is as follows
(1)Initialize samples using Latin Hypercube Sampling and evaluate them.Store samples and their responses in a database;
(2)Build Kriging meta-models for objectives based on the database;
(3)Calculate the boundary Pareto-optimal solutions by a single objective optimization approach;
(4)Evaluate the boundary Pareto-optimal solutions.Store them and their responses in the database and external archive;
(5)Prune the external archive;
(6)Calculate Pareto-optimal solutions through Kriging meta-model using MOPSO and the external archive;
(7)Evaluate Pareto-optimal solutions.Store them and their responses in the database and external archive;
(8)Prune the external archive;
(9)Calculate the trapezoid index for the external archive;
(10)If the trapezoid index is similar to that in the previous iteration,output the external archive.Otherwise,go to(2).
The database is used to store samples and their responses.In each iteration,obtained Pareto-optimal solutions should be evaluated,and then added into the database.During the optimization process,the number of samples increases,and Kriging meta-models have higher and higher accuracy around the Pareto-optimal solutions.
The external archive is used to store Pareto-optimal solutions.However,some Pareto-optimal solutions in the external archive may dominate some new ones or be dominated by some new ones.Thus,the external archive should be pruned after new members join.When running MOPSO,gbest iis selected from the external archive.
The trapezoid index tends to be stable as the process going on.If the trapezoid index is different only slightly from the one in previous step when new samples are added into the database and the Kriging meta-model updates,the optimization process is terminated.The trapezoid index can be regarded as a property of the Kriging meta-model.Trapezoid index’s stabilization means no more samples are needed and overshooting train of the Kriging meta-model is prevented.
4 Illustrative examples
In this section,four examples,taken from Ray and Liew’s study[18],are worked out based on M-MOPSO.The first is a two-objective minimizing problem with a discontinuous Pareto-optimal front.The second problem is the design of a welded beam.The third aims to design a multiple disc brake.The last problem deals with the designing of a four-bar truss.They are expressed as below
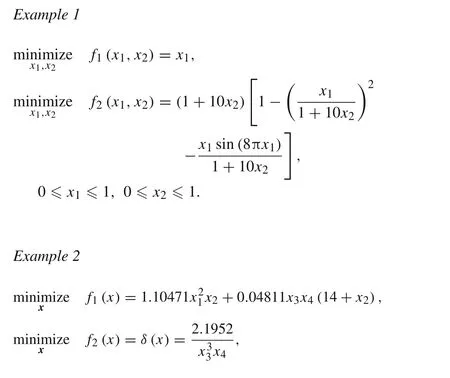

Assume that the maximum iteration is50.The number of particles for M-MOPSO and MOPSO is assigned to be 20 and 50,respectively.The group number of NSGA-II is assigned to be 50.The Pareto-optimal solutions obtained by M-MOPSO,MOPSO and NSGA-II are shown in Fig.2.
In each example,three sets of Pareto-optimal solutions obtained by M-MOSPO,MOPSO,and NSGA-II are shown in the objective space.For Example 1,there is little difference among the three sets of Pareto-optimal solutions.For Examples2 and 3,M-MOPSO can obtain the Pareto-optimal front more completely,while MOPSO and NSGA-II failed to do so.Regarding Example 4,the accuracy of the Paretooptimal solutions obtained by MOPSO and NSGA-II is much worse than that obtained by M-MOPSO.Evaluation number comparison is shown in Table 1.Using M-MOPSO,the evaluation number for each example is much less than when using MOPSO and NSGA-II.From these results,it is shown that computational efficiency and the accuracy of the Paretooptimal solutions have been greatly improved when using M-MOPSO as compared to MOPSO and NSGA-II.
For minimization problems,since the objectives are minimized,the corresponding trapezoid index is decreasing as the iteration proceeds.The decrease of trapezoid index for Example 4 is shown in Table 2.The optimization has been completed at the6th iteration.It can be seen that the trapezoid index at the 6th iteration is almost equal to the one at the 5th iteration.The convergence is judged,and no further iteration is needed.The trapezoid index of Pareto-optimal solutions obtained by MOPSO and NSGA-II is 24.8735 cm4/kN and 24.5903 cm4/kN,respectively,implying that although much greater evaluation number is involved,implying that the final Pareto-optimal solutions do not reach the Pareto front entirely for these two methods.
Since random coefficients are involved in MOPSO,50 optimization runs have been done for the illustrative examples.The expectations,standard deviations and coefficients of variation(COVs)of the trapezoid indexes are shown in Table 3.It can be seen that all of COVs for the four illustrative examples are small.It indicates that trapezoid indexes are similar to each other obtained by multiple optimization runs.The set of Pareto-optimal solutions obtained by M-MOPSO is reliable and the method proposed is robust enough.
5 Multi-objective optimization design for a deepwater composite riser
Nowadays,the offshore oil production industry is gradually moving into deeper water.Since the weight of a riser increases with water depth,traditional steel risers are heavy and require expensive tensioning and buoyancy systems.Compared to steel risers,composite risers offer many attractive properties,such as light mass,high corrosion resistance,and design flexibility.Because of the light mass,the demand of tension can be decreased.In addition,even though a composite’s cost is higher than that of steel,the cost of the entire ocean platform and tension riser may be substantially decreased.A tension riser system is shown in Fig.3.
Designing a composite riser involves difficulties due to the material’s anisotropy.In addition,multiple objectives conflict with each other.Traditional single objective optimization used in steel risers cannot reveal the relationship among multiple objectives.First,a composite riser works under toroidal pressure in the deepwater environment.The composite riser’s critical pressure should be greater than the toroidal pressure to avoid buckling.Second,a composite riser is under tension caused by the transportation of oil.A tension fracture will occur if a composite riser’s tensile strength cannot reach the requirement.Meanwhile,a lighter riser will decrease the cost of the tension riser and the ocean platform.These three factors conflict with each other.Thus,precisely how to design a composite riser to achieve a compromised relationship among these three factors is a challenge work that must be solved.In the following,M-MOPSO method proposed above is applied to solve the problem.
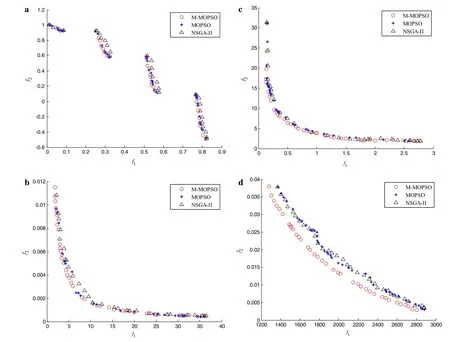
Fig.2 Pareto-optimal solutions obtained by M-MOPSO,MOPSO,and NSGA-II.a Example 1.b Example 2.c Example 3.d Example 4
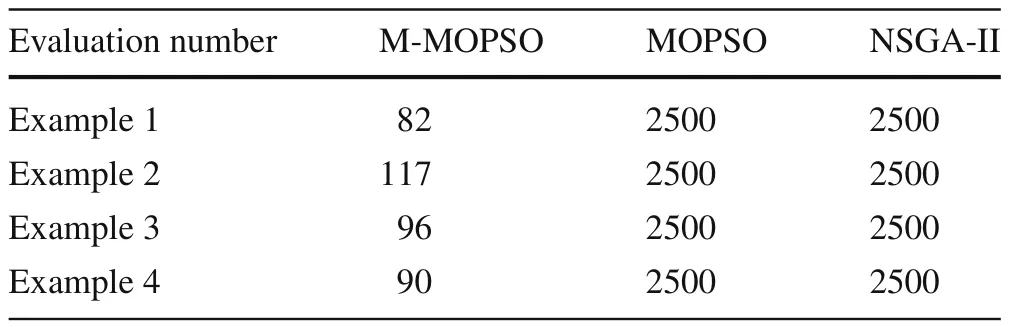
Table 1 Evaluation number comparison among M-MOPSO,MOPSO,and NSGA-II

Table 2 Trapezoid index in Example 4
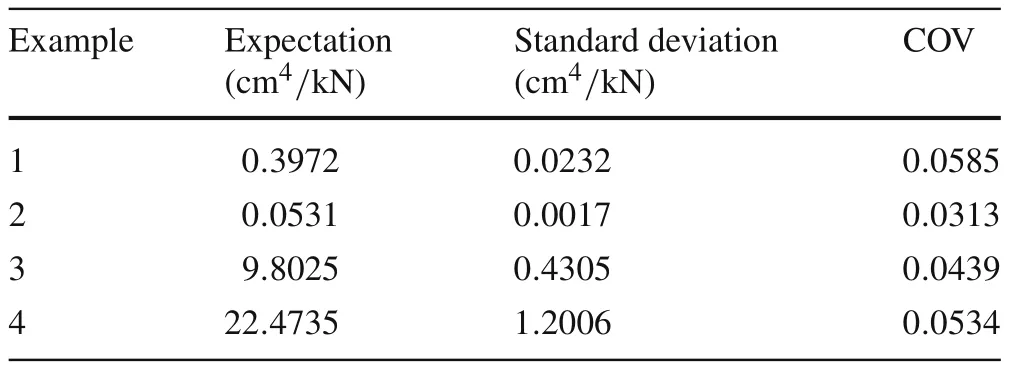
Table 3 Statistical analysis
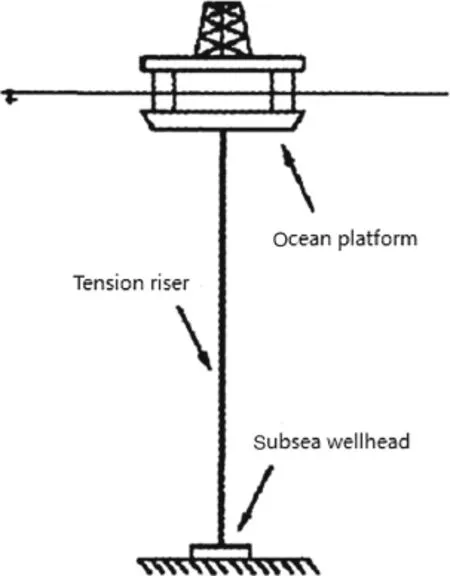
Fig.3 A tension riser system
In this paper,the Tsai–Wu failure criterion is used to estimate whether the composite riser exhibits a tensile fracture.
The Tsai–Wu failure criterion can be expressed as
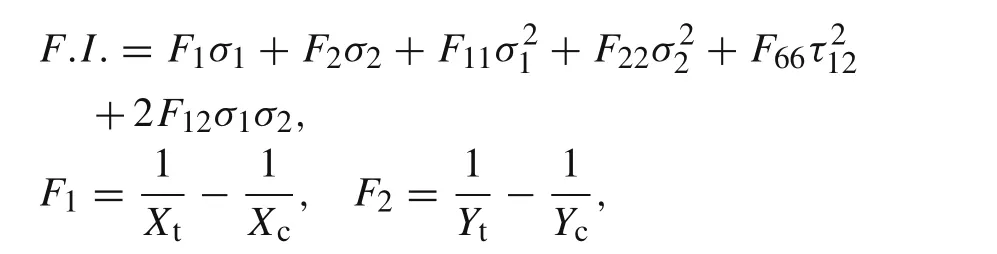

Fig.4 The finite element model of a composite riser
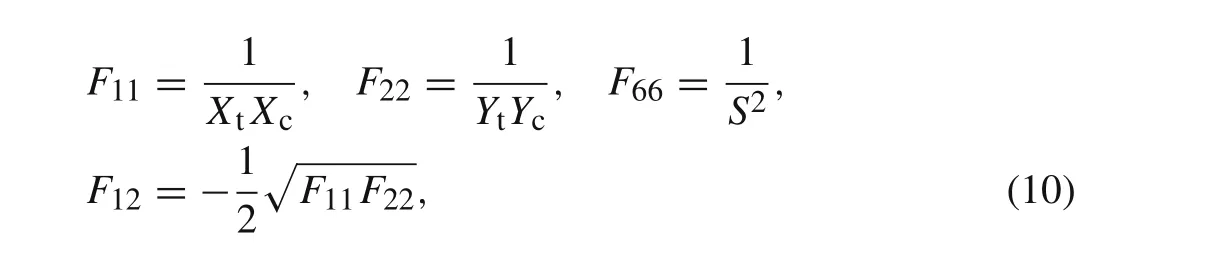
whereσ1andσ2are the fiber direction stress and transverse stress,respectively;andτ12is the shear stress.Five strength parameters take values as:Xt= 1516.9 MPa,Xc=1034.3 MPa,Yt=34.4 MPa,Yc=151.7 MPa,andS=69 MPa.
If the failure index(F.I.)of a layer is larger than 1,as a tensile fracture will occur.When the maximum F.I.of all layers is equal to 1,the tension that the composite riser sustains is defined as the tensile strengthT.
Filament’s material parameters take values as:E1=138.9 GPa,E2=6.62 GPa,υ=0.373,andG=2.96 GPa.
The design of the composite riser can be expressed as:

SinceT,V,andPreqare implicit,and their calculation requires calling finite element models,M-MOPSO method is used to solve Eq.(11).
The Kriging meta-models of tensile strengthT,material’s volumeV,and the critical pressurePreqare shown in Figs.5–7 based on the database in the last iteration.In Fig.5,the maximum tensile strengths are usually located at 0°regardless of the value ofh.Tensile strengthTincreases along withhincreasing.In Fig.6,it can be seen that the material’s volumeVis linear tohregard less ofθ.This comes from the fact that the composite riser is a shell structure,and both the cross-sectional area and the material’s volumeVare linear to the thickness.In Fig.7,it can be seen that the maximum critical pressure is usually located at the interval between 40°and 60°.The maximum critical pressure increases along withh.
Pareto-optimal solutions based on M-MOPS,MOPSO,and NSGA-II are shown in Fig.8,respectively.
In the objective space,there is a trade-off between the tensile strengthTand the material’s volumeV.There is an approximate linear relationship between the two objectives regardless of the methods used,i.e.,M-MOPSO,MOPSO,and NSGA-II.As the tensile strengthTincreases,the composite riser can sustain more tension under the condition that no buckling and fracture occur.However,the material’s volumeVincreases along with the tensile strengthT.Because of the increase of material’s volumeV,the cost of the composite riser will also increase.On the contrary,the decrease of tensile strengthTindicates that the oil’s transportation capability also decreases.The decision-maker can select a Pareto-optimal as the design solution among the Paretooptimal solutions.
As compared with MOPSO and NSGA-II,Pareto-optimal solutions obtained by M-MOPSO have larger tensile strengthTand smaller material’s volumeV.The function evaluation number is 94 as compared to 2500 in MOPSO and 2500 in NSGA-II.By applying MOPSO and NSGA-II,more evaluations are taken while the Pareto-optimal solutions are not as good as that of M-MOPSO,due to the premature convergency.This example is a black-box problem,and the function evaluation is based on finite element analysis.By introducing Kriging meta-models and the trapezoid index into MOPSO,the proposed M-MOPSO approach has a higher efficiency as compared to the MOPSO and NSGAII.
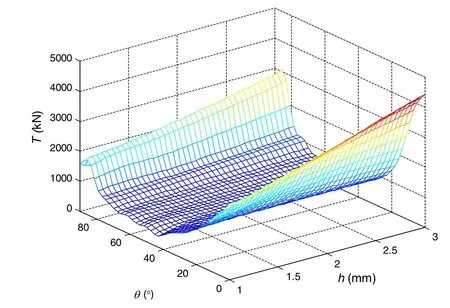
Fig.5 Kriging meta-model of tensile strength T
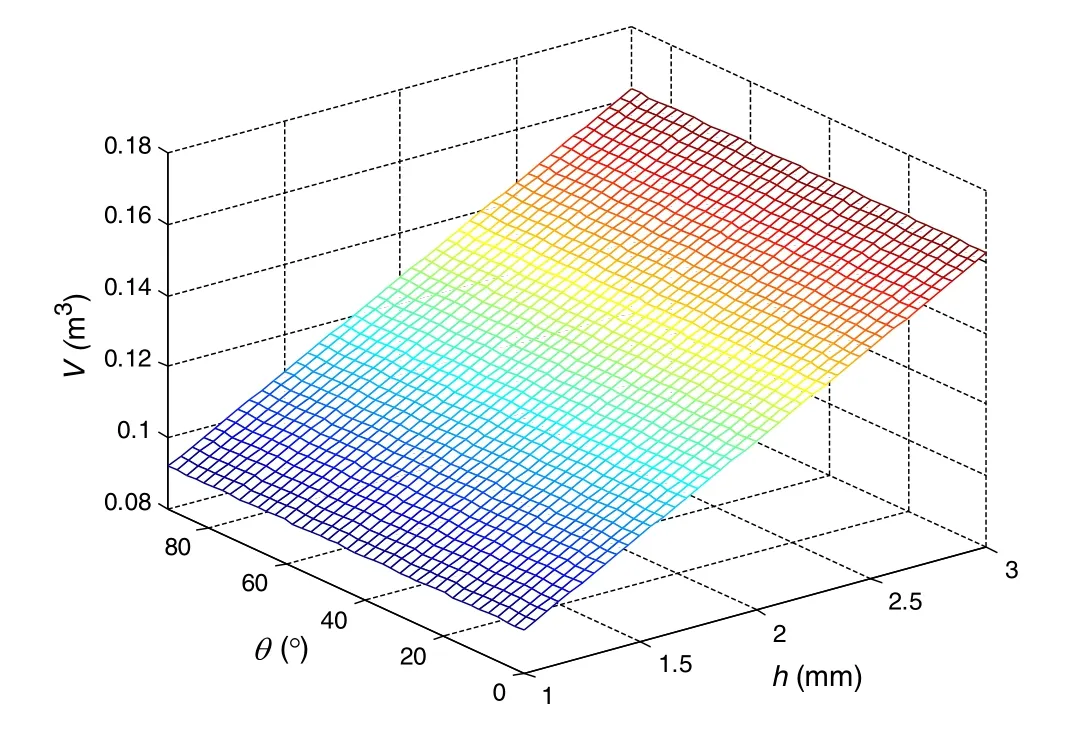
Fig.6 Kriging meta-model of materials volume V
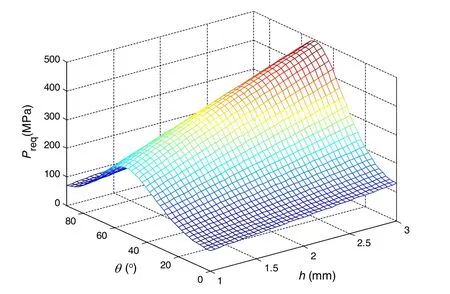
Fig.7 Kriging meta-model of critical pressure Preq
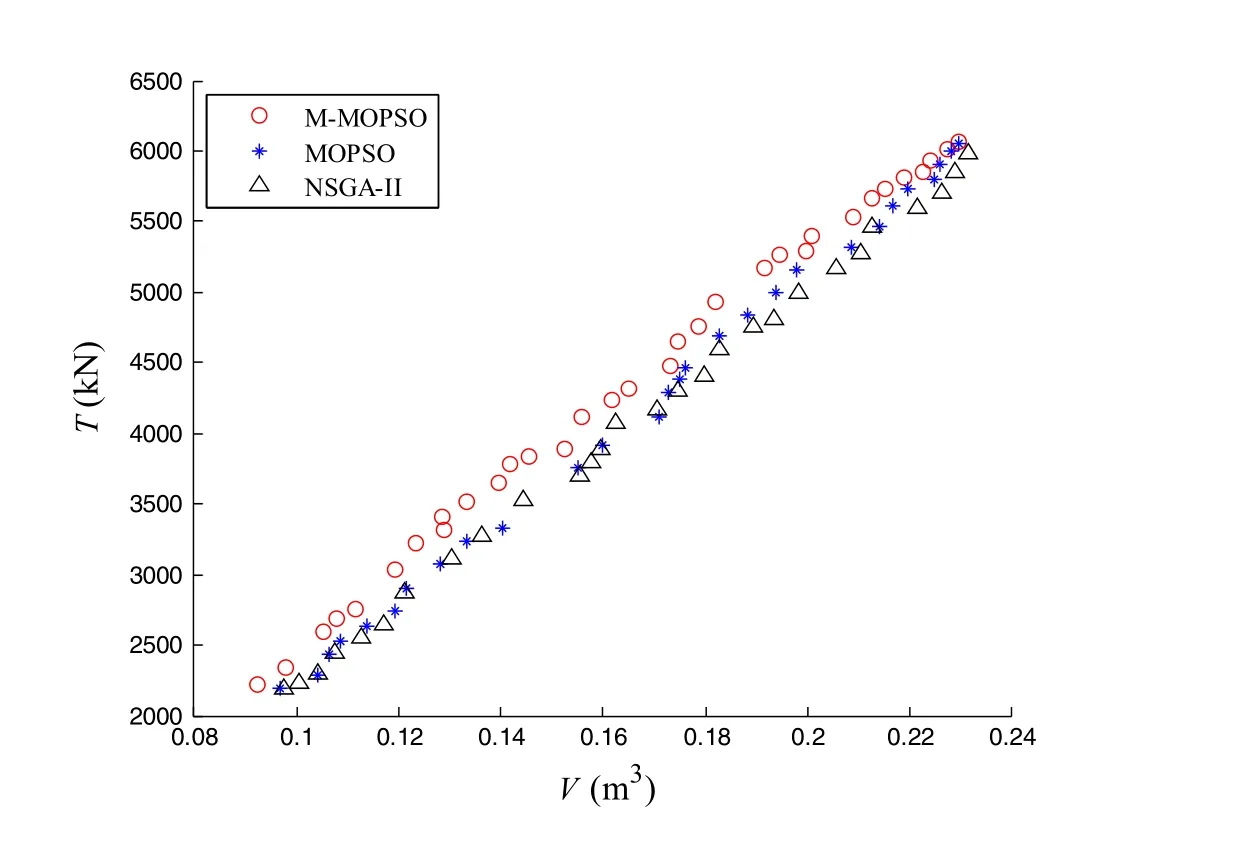
Fig.8 Pareto-optimal solutions in the objective space
The trapezoid index’s variation during the iteration using M-MOPSO is shown in Table 4.Different from the illustrative examples in Sect.4 in which both of two objectives are minimized,the tensile strengthTis maximized while material’s volumeVis minimized in this case.Therefore,the trapezoid index is increasing along with the iteration.It can be seen that the trapezoid index increases during the iteration and tends to be stable at the 5th iteration.By applying MOPSO and NSGA-II,the trapezoid indexes of the final Pareto-optimal solutions is 537.6567 and 534.1834 kN·m3,respectively,showing that the quality of their results is much worse than that of proposed method.
If the material’s volumeVis identified as the constraint,the multi-objective optimization problem will change to a single objective optimization problem.Only one solution can be obtained and it is one of the Pareto-optimal solutions.
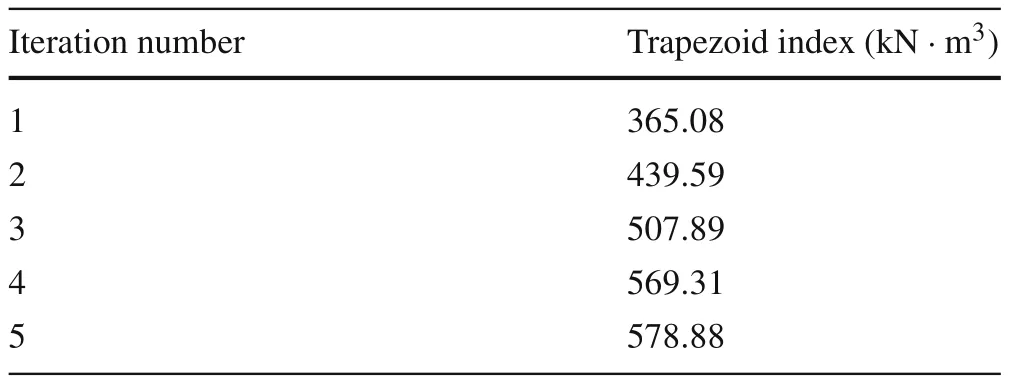
Table 4 Trapezoid index
6 Conclusions
In this paper,a modified multi-objective particle swarm optimization approach is developed in which Kriging meta models and the trapezoid index has been introduced into the traditional MOPSO.Kriging meta-models help to build surrogate models that replace expensive or black-box functions,and the trapezoid index assists to judge whether Paretooptimal solutions converge to the Pareto front and terminate the optimization process.Illustrative examples indicate that the evaluation number has been decreased largely by applying M-MOPSO as compared to the traditional MOPSO and NSGA-II.During the optimization process,the trapezoid index tends to be stable,indicating that the accuracy of the Kriging meta-model reaches a high level and the Paretooptimal solutions are closing to the Pareto front.The results of multiple optimization runs show that the variability of the trapezoid index of the final Pareto-optimal solutions is small enough,implying that the results are reliable and the proposed approach is robust.Considering a deepwater environment,a design of a composite riser has been presented.Its critical pressurePreq,tensile strengthT,and material volumeVshould be evaluated by finite element analysis.By using the proposed M-MOPSO,Pareto-optimal solutions are obtained by relatively small function evaluations with better quality.This indicates that M-MOPSO can handle these black-box multi-objective optimization problems effectively.How to define the trapezoid index for problems that include three or more objectives,and develop more efficient multi-objective optimization method constitute our future work.
AcknowledgementsThis work was supported by the National Natural Science Foundation of China(Grant 11572134).
1.Deb,K.,Pratap,A.,Agarwal,S.,et al.:A fast and elitist multiobjective genetic algorithm:NSGA-II.IEEE Trans.Evol.Comput.6,182–197(2006)
2.Zitzler,E.,Laumanns,M.,Thiele,L.:SPEA2:improving the strength Pareto evolutionary algorithm.Computer Engineering and Networks Laboratory(TIK)-Report 103,Switerland,May(2001)
3.Kennedy,J.,Eberhart,R.C.:Particle swarm optimization.In:Proceedings of the IEEE International Conference on Neural Networks,Piscataway,NJ,1942–1948(1995)
4.Khalili-Damghania,K.,Abtahil,A.R.,Tavana,M.:A new multiobjective particle swarm optimization method for solving reliability redundancy allocation problems.Reliab.Eng.Syst.Saf.111,58–75(2013)
5.Garg,H.,Sharma,S.P.:Multi-objective reliability-redundancy allocation problem using particle swarm optimization.Comput.Ind.Eng.64,247–255(2013)
6.Zhang,Y.,Gong,D.W.,Ding,Z.:Abare-bonesmulti-objective particle swarm optimization algorithm for environmental/economic dispatch.Inf.Sci.192,213–227(2012)
7.Abido,M.A.:Two-level of nondominated solutions approach to multiobjective particle swarm optimization.In:Proceedings of the Genetic and Evolutionary Computation Conference(GECCO-2007),London,UK,726–733.Assoc Computing Machinery,New York,July,2007
8.Branke,J.,Mostaghim,S.:About selecting the personal best in multi-objective particle swarm optimization.In:Proceedings of the 9th International Conference on Parallel Problem Solving from Nature(PPSNIX),Reykjavik,Iceland,523–532.Springer,Berlin(2006)
9.Coello,C.A.C.,Pulido,G.T.,Lechuga,M.S.:Handling multiple objectives with particle swarm optimization.IEEE Trans.Evol.Comput.8,256–279(2004)
10.Zhao,S.Z.,Suganthan,P.N.:Two-lbestsbased multi-objective particle swarm optimizer.Eng.Optim.43,1–17(2011)
11.Mostaghim,S.,Teich,J.:Strategies for Finding Good Local Guides in Multi-objective Particle Swarm Optimization.In:Swarm Intelligence Symposium 2003,Indianapolis,USA(2003)
12.Regis,R.G.:Evolutionary programming for high-dimensional constrained expensive black-box optimization using radial basis functions.IEEE Trans.Evol.Comput.18,326–347(2014)
13.Akhtar,T.,Shoemaker,C.A.:Multi objective optimization of computationally expensive multi-modal functions with RBF surrogates and multi-rule selection.J.Glob.Optim.64,17–32(2016)
14.Isaacs,A.,Ray,T.,Smith,W.:Multi-objective design optimization using multiple adaptive spatially distributed surrogates.Int.J.Prod.Dev.9,188–217(2009)
15.Ray,T.,Smith,W.:A surrogate assisted parallel multi-objective evolutionary algorithm for robust engineering design.Eng.Optim.38,997–1011(2006)
16.Emmerich,M.T.M.,Giannakoglou,K.,Naujoks,B.:Single-and multi-objective evolutionary optimization assisted by Gaussian random field meta-models.IEEE Trans.Evol.Comput.10,421–439(2006)
17.Singh,P.,Couckuyt,I.,Ferranti,F.,et al.:A constrained multiobjective surrogate-based optimization algorithm.In:Proceedings of 2014 IEEE Congress on Evolutionary Computation(CEC),3080–3087.IEEE(2014)
18.Ray,T.,Liew,K.M.:A swarm metaphor for multi-objective design optimization.Eng.Optim.34,141–153(2002)
- Acta Mechanica Sinica的其它文章
- Measurement of the flow structures in the wakes of different types of parachute canopies
- Effect of perforation on flow past a conic cylinder at Re=100:vortex-shedding pattern and force history
- Mobile bed thickness in skewed asymmetric oscillatory sheet flows
- Mechanical properties of gas hydrate-bearing sediments during hydrate dissociation
- Reliability-based multidisciplinary design optimization using incremental shifting vector strategy and its application in electronic product design
- Time-varying nonlinear dynamics of a deploying piezoelectric laminated composite plate under aerodynamic force

