Reliability-based multidisciplinary design optimization using incremental shifting vector strategy and its application in electronic product design

Z.L.Huang·Y.S.Zhou·C.Jiang·J.Zheng·X.Han

1 Introduction

Asa kind of advanced design method based on the integration of disciplinary analysis and optimization,multidisciplinary design optimization(MDO)is currently being widely applied in various industrial fields[1–4].The term “multidisciplinary”indicates that multiple engineering disciplines are involved in the design problem,where the result of analysis for each discipline is obtained using related theory as well as simulation tools.Meanwhile,complex coupling relationships between disciplines are also involved.By exploring and utilizing the coupling mechanisms of these interactions between disciplines,MDO methods[5]can address this type of complex problem.In recent years,MDO has become an important research direction in optimization design,and a series of theories and methods[6,7]have been developed in this area.These algorithms can be roughly grouped into two categories,viz.single-[8–10]and multilevel optimization methods[11–13].The former is mainly used to deal with problems with few design variables and disciplines,in which design optimization is performed by considering the system as a whole;in contrast,in the latter,the optimization is carried out for each discipline alone,then consistent design is carried out to obtain optimal solutions at system level.Commonly used single-level methods include the individual disciplinary feasible(IDF)approach[8],the all-at-once(AAO)approach[9],the multidisciplinary feasible(MDF)approach[10],etc.,while multilevel optimization methods mainly include the concurrent subspace optimization(CSSO)approach[11],the collaborative optimization(CO)approach[12],the bilevel integrated system synthesis(BLISS)approach[13],etc.The traditional MDO methods mentioned above were developed mainly to solve deterministic problems,in which all of the parameters are deterministic rather than random or uncertain.However,in practical engineering problems,there exist many uncertainties,including structural sizes,material properties,and loads.The combined effects of these uncertain factors can lead to large variations and even failure of the structure.Studies have shown that addressing such uncertainty-based multidisciplinary problems using conventional MDO methods may result in unreliable design[14].

Reliability-based design optimization(RBDO)can fully take into account the impacts of parametric uncertainties on the constraints during the optimization process[15–22],thereby achieving a reliable design.Thus,the RBDO method currently plays an important role in safe design of complex structures.In recent years,with the introduction of RBDO for multidisciplinary problems,reliability-based multidisciplinary design optimization(RBMDO)has been proposed and developed,becoming a significant research direction.An RBMDO algorithm in which the system reliability analysis was decoupled from the MDO and the efficiency was improved to a great extent was presented by Sues and Cesare[23].Monte Carlo simulation was selected as a suitable technique by Padmanabhan et al.[24]to easily calculate the analytical sensitivity of the failure probability,thereby overcoming to some extent the convergence problems caused by discontinuous constraint functions.Surrogate models were adopted by Agarwal and Renaud[25]to replace the time consuming computations of performance functions,greatly reducing the computational cost.Moreover,the BLISS strategy of MDO was integrated into the RBDO framework and the trust-region-based response surface methodology used to improve the efficiency of RBMDO analysis by Ahn and Kwon[26].An RBMDO framework based on sequential optimization and reliability assessment(SORA)was proposed by Du et al.[27],in which two decoupling strategies were considered for problems with different levels of complexity of multidisciplinary analysis.A subset-simulation based reliability analysis(SSRA)approach was employed by Meng et al.[28]to formulate a new RBMDO method and applied to the design of a hydraulic transmission mechanism.Transformation of each probabilistic constraint into multiple single-variable monotonic problems using a gradient-based transformation strategy was applied by Lin and Gea[29],using parallel computation for high efficiency.RBMDO analysis based on the adaptive response surface was carried out by Xiao et al.[30]for the structural design of a transport aircraft wing,effectively increasing the cruise range of the aircraft.The multidisciplinary problem of an aeroelastic system was analyzed by Nikbay and Kuru[31]by considering the coupling mechanism between structural mechanics and aerodynamics.The above-cited studies have effectively expanded the application of reliability-based design approaches to multidisciplinary problems,thus improving the engineering design capability for practical complex systems.However,due to the complexity of RBMDO problems,some crucial technical issues remain to be solved in this area.Firstly,even for traditional RBDO problems,the high computational cost caused by the nested optimization has proved to be a difficulty,while in RBMDO this efficiency problem is further exacer bated,because multiple simulation models corresponding to different disciplines are introduced,and more importantly,complex decoupling relationships exist among these models.This complexity results in great challenges to solution of RBMDO problems in terms of not only efficiency but also convergence.Secondly,although RBMDO methods have been applied to some engineering problems in literature,most of them are actually based on many simplifications and assumptions,and some disciplines in these applications are even based on empirical formulas or analytical functions.To date,few RBMDO models for practical engineering problems,in which high-precision simulation models are created for different disciplines and furthermore strong coupling relationships exist among these disciplines,have been described.Indeed,in recent years,the practicability of RBMDO has even been questioned to some extent.Thus,to promote development of RBMDO,not only more efficient and stable solution algorithms for RBMDO must be proposed,but also more convincing engineering applications must be considered.

In this paper,the incremental shifting vector(ISV)strategy[32],recently proposed by the authors,is expanded to the MDO problem,leading to the development of a new RBMDO algorithm with high efficiency and good convergence.Furthermore,the proposed method is successfully applied to the design of two actual electronic products,viz.an aerial camera and a car pad.The remainder of this paper is organized as follows:the general concept of MDO,as well as the mathematical model of RBMDO,is introduced in Sect.2;the proposed method is formulated in Sect.3;one simple numerical example and two complex engineering problems are investigated in Sect.4 to demonstrate the validity of the proposed method;finally,Sect.5 presents the conclusions of this work.

2 RBMDO problem statement

In this paper,a system involving three disciplines,as shown in Fig.1,is taken as an example to illustrate a conventional deterministic MDO problem.The input of the multidisciplinary system is ann d-dimensional deterministic design vectord,while the outputs are the objective functionfand the constraintsg j,j=1,2,...,n g,wheren gdenotes the number of constraints.Each solid-line box represents an analysis process of the corresponding discipline;the analysis for each discipline is assumed to output only one constraint for the sake of descriptive convenience;g j?0 indicatesthatthe design option meets the requirement of thej-th discipline;the general cases involving more constraints follow the same theory.fjdenotes the objective function based on the analysis of thej-th discipline,being viewed as part of the system objective functionf=f(d,f1,f2,f3).Unlike in conventional deterministic optimization,the state vectory jiexists in the MDO problem,denoting the output of thej-th constraint as well as the input of thei-th constraint;in other words,during the analysis for one discipline,the influence of the other disciplines must also be considered,and multiple disciplines are coupled through the interaction of the state vectorsy ji,whence the name “coupling vectors.”Moreover,fj,g j,andy jican be obtained according to the relevant theory or analysis tool of thej-th discipline.To provide a more intuitive explanation,the expanded forms of these items are listed in Table 1.The conventional deterministic MDO problem can then be formulated as[8]

Fig.1 Traditional deterministic MDO

where the superscripts “l”and “u”denote the range of the design variable values.

Practical multidisciplinary problems usually involve many uncertainties,e.g.,in material parameters,loads,etc.To meet the reliability requirements of such a multidisciplinary system,the effects of these uncertainties on system performance should be fully taken into consideration during the optimization process.An uncertain variable can usually be treated as a random variable that follows a given type of probability distribution.In this way,Eq.(1)can be transformed into an RBMDO,being generally expressed as follows[27]

whereXis then X-dimensional random design vector,Pdenotes then P-dimensional random parameter vector,μrepresents the mean vector of a random vector,Pr means the probability measure,R jrepresents the probability of constraint satisfaction,also called the reliability,andRtjis the target reliability degree of thej-th constraint.It should be pointed out that,due to the existence ofX,P,the objective function valuefjand the coupling vectory jiare both theoretically random.To reduce the problem complexity,μXandμPare generally used to calculatefjandy ji,respectively.

As shown in Fig.2,similar to the conventional RBDO,RBMDO involves a two-layer nested optimization[27],with the outer layer being the optimization for the design variables and the inner layer being the constraint reliability analysis.The difference lies in that the constraint reliability analysis involves multidisciplinary problems and that these disciplines are coupled via state variables;For example,the outputy12of the first discipline is a requisite input for the analysis of the second discipline,and vice versa.As a result,the multidisciplinary analysis must be repeated to coordinate the analysis result of each discipline to achieve consistency of the state variables.However,the performance functions of practical problems generally require time-consuming simulation techniques,thus such repeated calculations of the simulation models can lead to extremely low computational efficiency.Therefore,RBMDO represents a more challenging problem than conventional RBDO.

3 Proposed RBMDO method

To improve the computational efficiency,an RBMDO decoupling algorithm based on an ISV strategy[32],recently proposed by the authors,is developed herein.As shown in Fig.3,its basic idea is that the original RBMDO problem isfirst converted into a conventional RBDO formulation using the IDF approach,then the ISV strategy is used to solve the resulting RBDO efficiently.

Table 1 State variables,objective functions,and constraints in MDO

Fig.2 RBMDO problem involving three disciplines

3.1 Conversion to conventional RBDO form

The core issue in multidisciplinary analysis is to deal with the coupling relationships between the disciplines,namely to achieve consistent design of the state variables in each discipline.A series of important approaches for MDO have now been developed,including the IDF approach[8],the AAO approach[9],the CO approach[12],the BLISS approach[13],etc.Among these,the IDF approach is one of the MDO algorithms that are widely applied[33].In IDF,the multidisciplinary problem is decoupled by adding new design variables and consistency constraints,so that the analysis of each discipline can be carried out independently.The implementation of the IDF approach is simple and easy,and is particularly convenient when utilizing commercial simulation tools.Thus,the IDF strategy is employed in this study to deal with the multidisciplinary problem.Specifically,a new design variable is added for each state variable,and a corresponding consistency constraint is set to eliminate the difference between the state variable and the new design variable;For example,the deterministic design way,Eq.(2)can be transformed into a conventional RBDO problem

wherev jiis the newly added deterministic design vector,h vjiis the consistency constraint,and?·?denotes vector modulus.

Using this transformation process,the multidisciplinary analysis in Eq.(2)can be decoupled.However,Eq.(3)is still a nested optimization problem,and a large amount of calculations is required to solve it.Moreover,a certain number of design variables and constraints are newly introduced into Eq.(3)compared with Eq.(2),further increasing the difficulty of solving the problem.

3.2 Decoupling strategy

Fig.3 Framework of proposed method

The ISV approach[32]is a decoupling algorithm,recently proposed by the authors,exhibiting good overall performance in terms of efficiency and convergence for problems with relatively large number of variables and constraints.In ISV,the nested optimization problem in Eq.(3)is decoupled into a sequential iteration process composed of design optimization and reliability analysis.In the design optimization stage,each probabilistic constraint is transformed into a deterministic constraint,and a new design point is obtained by solving the deterministic optimization problem.In the reliability analysis stage,reliability assessment is carried out on the new design point,and a shifting vector is calculated,providing the information required for the equivalence of the constraints in the next iteration.The design optimization and reliability analysis are conducted alternately until convergence is achieved.

Fig.4 The equivalence process of the deterministic constant

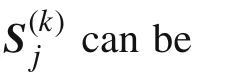
whereh Z(Z)denotes the joint probability density function(PDF)ofZ.

The reliability index approach(RIA)[34,35],which is one of the first-order reliability methods(FORMs),is used to deal with the problem in Eq.(6).Firstly,the random variableZ iis transformed to the standard normal random variableUi,which can be expressed as follows

whereG jrefers to the constraint functiong jin theU-space,h Ustands for the joint PDF ofU,andβtjis the target reliability index of thej-th constraint.Note thatG jis related tok,because the design point is updated.Secondly,the linear approximation ofG jis established at the most possible point(MPP);geometrically,the distance from the MPP to the originU0is the smallest distance betweenG jandU0,and the value of this distance is the reliability indexβ(k)j.This mathematical model can be expressed as follows

Fig.5 Approximate reliability analysis

In RIA,Eq.(9)can also be formulated as an optimization problem[34,35]

wherenrepresents the Newton iteration step.

3.3 Computational procedure

To summarize,a flowchart of the proposed RBMDO method is provided in Fig.6 and summarized in the following steps:

Step 1:Formulate the RBMDO model shown in Eq.(2)by analysis of the engineering problem.

Step 2:Decouple the multidisciplinary analysis,and transform Eq.(2)into the conventional RBDO problem in Eq.(3).

Fig.6 Computational flowchart of proposed method

畜作为畜牧系统来说，局档案是一个非常重要的东西，她是关系到畜牧业研究和建设的重要材料。它涉及到的范围比较广泛，比如，育种、饲养和防治等等。因此，作为畜牧局档案工作是国家的一个十分珍贵的科技资料财富，更是难得的科技资源。如何做好畜牧局档案工作是一项非常重要的工作。本文笔者就此进行了认真地尝试和总结。

Step 4:Carry out the constraint reliability analysis,and setk:=k+1;Equation(12)is adopted to conduct the reliability analyses for each constraint on the optimal solution in the previous iteration.Then,the reliability indexesβ(k)j,j=1,2,...,n gare obtained.

Step 5:Calculate the shifting vector.The reliability is judged

Step 7:Repeat the fourth to sixth step until the following two convergence conditions are met

It is worth noting that,in the above process,all random variables inXorPare assumed to be independent.If this is not so,the orthogonal transformation[38]can be applied to eliminate the correlation between them,so that the proposed method can still work.

4 Numerical examples and discussion

4.1 Test example

The test example displayed in Eq.(17)is first considered,modified from an existing example in Ref.[27].The example includes a three-dimensional random design vectorX=[X1,X2,X3]and a three-dimensional random parameter vectorP=[P1,P2,P3];the mean and standard deviation of the random vectors are denoted byμandσ,respectively.Also,two disciplines,which are coupled by the state variablesy12,y21,are involved in this computation example;the constraint reliability valuesR1andR2and the objective functional valuesf1andf2are obtained by analysis of the two disciplines.Furthermore,the objective functionfof the system is formulated by the summary off1andf2.This RBMDO problem can be expressed as follows

Table 2 Computational results for test example

The IDF strategy is employed to decouple the multidisciplinary analysis,then Eq.(17)is transformed into the following equation

To investigate the characteristics of the proposed method,the IDF-SORA method[27]was used for comparison.IDFSORA is an efficient decoupling algorithm for RBMDO,in which the SORA strategy is introduced to decouple the nested optimization while the IDF algorithm is adopted to handle the multidisciplinary problems in both the design optimization a few iterative steps.Secondly,the solution of the proposed method is very close to that of IDF-SORA,with almost no difference between their objective functional values.Thirdly,the number of evaluations of the performance functional(141 times)in the proposed method is about one-third that of the IDF-SORA method(438 times).Compared with IDF-SORA,this shows to some extent that the proposed method possesses not only similar properties in terms of convergence and accuracy but also a significant advantage in terms of efficiency.

4.2 Structural design of aerial camera

An aerial camera system[39],as a new widely applied technology,usually uses an unmanned aerial vehicle as its aerial platform and an aerial camera to acquire ground image information.As one of the most important electronic devices in the aerial camera system,the aerial camera must continue to offer stable and reliable performance under extreme conditions.In the design of the aerial camera,several electronic modules are highly integrated,including a high-definition image sensor,signal processor,and codec.During the operation of such a camera,various extreme conditions are coupled with each other,including vibration of the aerial platform,changes of ambient temperature,and fluctuation of power consumption.Consequently,the structural design of the aerial camera generally involves multidisciplinary analysis,with the design results playing a key role in the overall performance of the camera.

As shown in Fig.7,an ultrahigh-definition aerial camera is considered in this paper,mainly comprising the following modules:lens,motherboard,filter,and housing.During the operation of the camera,two extreme conditions,viz.high temperature and vibration,are to be faced simultaneously.Temperature–displacement analysis for the high-temperature condition reveals that,under the interaction of the changing ambient temperature and the self-heating of components,significant temperature differences and thermal deformations will occur inside the camera.At the same time,dynamic mechanical analysis under vibration shows that different stress–strain responses of the camera structure will be generated for vibrations at different frequencies.When the conditions of high temperature and vibration coexist,the thermal deformation will exert a significant effect on the dynamic mechanical analysis,thereby becoming its required input.Meanwhile,the stress–strain response caused by vibration will also change the analysis result for the temperature and displacement of the camera;For example,deformation of the motherboard of the camera will lead to fluctuation of the power dissipation from the central processing unit(CPU),thus changing the internal temperature response of the camera.

Fig.7 Camera on unmanned aerial vehicle.a An unmanned aerial.b The aerial camera

Fig.8 Multidisciplinary analysis of aerial camera

Table 3 Random variables and distributions in aerial camera design

Fig.9 FEM model of aerial camera.a Profile view.b Sectional view

Fig.10 FEM analysis of aerial camera under different conditions.a High-temperature condition.b Vibration condition

The multidisciplinary analysis for the structural design of the aerial camera is decoupled using the IDF strategy,thus Eq.(19)is transformed into the following equation

wherev12andv21are the newly added design variables,corresponding to the coupling variablesDCPUandPCPU,respectively.

An FEM for the aerial camera was built as shown in Fig.9,including seven parts and 204,160 eight-node coupled temperature–displacement elements.By setting different boundary conditions,the FEM of temperature–displacement under the high-temperature condition and the FEM of dynamic mechanical response under the vibration condition can be obtained,as presented in Fig.10.To parameterize the solving process,the second-order polynomial response surfaces of the performance functionsTCPU,DMB,DCPU,PCPUwere obtained based on sampling of the FEMs for 65 times,as formulated in Table 4.Note that the formulation of such a response surface is not a necessary step for the proposed method.To test the accuracy of the response surfaces,six points were randomly selected in the design space and the results of the response surfaces and the FEMs were compared at these points,as presented in Table 5.The results show that,to some extent,each response surface exhibits acceptable accuracy with maximal error not exceeding 5%.

Table 4 Response surfaces of performance functions in aerial camera design

Table 5 Accuracy test of response surface models of aerial camera design

Table 6 Optimization results for aerial camera design

Fig.11 RBMDO iteration process of aerial camera design

4.3 Structural design of car pad

A car pad can provide various auxiliary functions for drivers,such as parking assistance,navigation,communication,and entertainment for the driver,thereby promoting their driving experience to a great extent.Car pads are now widely applied in various car electronic systems[41].Compared with general consumer electronic products,a car pad must adapt to various extreme working environments,including changing ambient temperature,multifrequency vibration,exposure to complex electromagnetic radiation,etc.Besides,the structural size of the car pad usually faces strict limits,thus being characterized by high integration and high power density.The structural design of an eight-inch car pad,as illustrated in Fig.12,is considered herein.The car pad mainly comprises the following parts:touch panel,display,power supply,motherboard,driver board,bracket,front housing,back housing,etc.As the core device of the car electronic system,the car pad must operate stably and reliably under conditions of high temperature and multifrequency vibration.Under conditions of high temperature and heat dissipation from internal electronic components,thermal stress and deformation will occur inside the car pad.Meanwhile,under vibrations at different frequencies,different stress–strain responses will emerge in the internal structure of the car pad.Note that the overall heat dissipation from the car pad depends primarily on the heat exchange between the back housing and the installation platform for the car pad,with surface contact stress having very important effects on such heat exchange.Furthermore,the power consumption of the motherboard will fluctuate due to the change of its own temperature and stress,thereby exerting reverse influences on the temperature and stress responses in the car pad.

As shown in Fig.13,the design vectorX=(X1,X2,X3,X4)for this multidisciplinary problem includes the front housing side-wall thicknessX1,the front-housing end-wall thicknessX2,the back-housing wall thicknessX3,as well as the bracket thicknessX4.In the parameter vectorP=?PD,EC?,PDrepresents the power dissipation of the driver board andECdenotes the elasticity modulus of the housing material.The objective function is the weight of the car pad.This multidisciplinary problem involves three disciplines coupled with each other:discipline_1 is the temperature–displacement analysis under the condition of ambient temperature of 55°C;discipline_2 is dynamic mechanical analysis under the condition of vibration in the frequency range of(40 Hz,160 Hz);discipline_3 is the power dissipation analysis for the graphics processing unit(GPU)and CPU on the motherboard.Among these,discipline_1 is coupled with discipline_2 throughDMB,σC,where the variableDMBstands for the maximal thermal deformation of the motherboard under high-temperature loading and the vectorσCrefers to the stress response of the housing under vibrational loading.For analysis conve-the design vectorXand parameter vectorPare random vectors,whose specific distribution information is presented in Table 7.The target reliability values for the constraints are set asβt1=βt2=2.5.To sum up,the RBMDO mathematical model can be constructed as follows

Fig.12 Eight-inch car pad.a Profile view.b Exploded view

Fig.13 Multidisciplinary analysis for car pad

Table 7 Random variables and distributions in car pad design

Fig.14 FEM model of car pad.a Profile view.b Sectional view

The FEM was built as shown in Fig.14 for the design of the car pad,containing ten parts and 285,708 eight-node coupled temperature–displacement elements.By setting different boundary conditions for the FEM,the FEMs shown in Fig.15 under the two conditions of high-temperature and vibration were obtained,while by constructing a test model for the power dissipation of the car pad,actual test values including the temperature,stress,as well as CPU and GPU power dissipation can be obtained.Furthermore,to parameterize the optimization,the second-order polynomial response surfaces of each performance function were formulated based on sampling of the FEMs or the actual test model for 65 times.Information related to the response surfaces is provided in Table 8.Subsequently,to test the accuracy of the response surfaces,six points were randomly selected in the design space,and the results of the response surfaces and the FEMs(or test models)were compared at these points,as presented in Tables 9 and 10.It can be seen that the maximal error was less than 5%,and the accuracy of the response surfaces is acceptable for the application to some extent.

To further indicate the importance of performing RBMDO,two solving situations for the practical problem were considered.In situation_1,the proposed method was used to carry out the RBMDO for Eq.(22);similarly,the reference solution from the double-loop method was employed to verify the accuracy of the proposed method.In situation_1,the coupling variables are assumed to be constants to avoid the original multidisciplinary analysis,hence the RBDO method can be conducted directly to solve Eq.(21).Specifically,engineering experience shows that,the larger the power dissipation of the car pad and the smaller the contact stress between the heat transfer surfaces,the easier it will be for the two constraints to fail.Therefore,it is reasonable that the maximal power dissipation of the chips obtained based on the actual test models and the minimal contact stress on the back-housing surface can be set as assumptive constants for the corresponding coupling variables,which is selected for the two solving situations.All the results are presented in Table 11,while the iterative process of the proposed method is shown in Fig.16.Firstly,the following findings can be made based on comparison of the results of the two RBMDO methods:in terms of accuracy,the optimal car pad weight obtained using the proposed method and the double-loop method are very close,namely 1.604 kg and 1.605 kg,respectively;in terms of convergence,the proposed method achieves convergence to the stable solution after only three iteration steps;in terms of efficiency,the number of evaluations of the performance functional(1210)for the proposed method is only 2.6%of that(47,369)of the double-loop method.These results show objectively that the proposed method can not only ensure convergence and accuracy but also achieve high efficiency.Secondly,it is found that,without considering the coupling relationships existing between disciplines,no feasible solution can be obtained by the conventional RBDO.According to the comparison between the com-0.20 MPain the RBDO,obvious difference can be seen between each computational value and the corresponding hypothetical constant.This occurs because engineers usually set hypothetical constants as conservative values,to ensure a safe design,whereas in the design of complex products,conservative assumptions for loads may lead to the feasible domain becoming smaller,and even disappearing.Thus,the necessity and effectiveness of RBMDO in practical applications are further verified.

Fig.15 FEM analysis of car pad under different conditions.a High-temperature condition.b Vibration condition

Table 9 Points for accuracy testing of response surfaces in car pad design

Table 10 Accuracy test of response surface models in car pad design

Table 11 Optimization results for car pad design

Fig.16 RBMDO iteration process of car pad design

5 Conclusions

An RBMDO approach is proposed to provide an efficient potential tool for reliability-based design of complex systems or products.The IDF strategy is employed to decouple the multidisciplinary analysis,transforming the original RBMDO into a conventional RBDO problem.The ISV strategy is then used to solve the resulting RBDO problem by converting the nested optimization into a sequential iterative process composed of deterministic optimization and reliability analysis stages.The proposed method was successfully applied to the design of two actual electronic products,an aerial camera and a car pad.For these two applications,high-precision simulation models were created for different disciplines with relatively strong coupling relationships among the involved disciplines.The analysis results show that,compared with the conventional double-loop method,the proposed method not only offers a significant advantage in terms of efficiency but could also meet the requirements of practical applications in terms of both accuracy and convergence.In the future,the proposed method could be further expanded to other MDO strategies,such as AAO,CO,and BLISS,to create corresponding RBMDO algorithms.

AcknowledgementsThe project was supported by the Major Program of the National Natural Science Foundation of China(Grant 51490662),the Funds for Distinguished Young Scientists of Hunan Province(Grant 14JJ1016),the State Key Program of the National Science Foundation of China(11232004),and the Heavy-duty Tractor Intelligent Manufacturing Technology Research and System Development(Grant 2016YFD0701105).

1.Jaroslaw,S.,Raphael,T.H.:Multidisciplinary aerospace design optimization:survey of recent developments.Struct.Multidiscip.Optim.14,1–23(1997)

2.Duddeck,F.:Multidisciplinary optimization of car bodies.Struct.Multidiscip.Optim.35,375–389(2008)

3.Li,F.,Li,G.,Sun,G.,et al.:Multidisciplinary optimization for multi-objective uncertainty design of thin walled beams.Comput.Mater.Contin.19,37–56(2010)

4.Ma,M.:Multidisciplinary design optimization for complex product review.Chin.J.Mech.Eng.44,15–26(2008)

5.Balling,R.J.,Sobieszczanski-Sobieski,J.:An algorithm for solving the system-level problem in multilevel optimization.Struct.Optim 9,168–177(1995)

6.Viana,F.A.C.,Simpson,T.W.,Balabanov,V.,etal.:Specialsection on multidisciplinary design optimization:meta modeling in multidisciplinary design optimization:how far have we really come?AIAA J.52,670–690(2014)

7.Tedford,N.P.,Martins,J.R.R.A.:Benchmarking multidisciplinary design optimization algorithms.Optim.Eng.11,159–183(2010)

8.Lewis,R.M.,Shubin,G.R.,Cramer,E.J.,et al.:Problem formulation for multidisciplinary optimization.SIAMJ.Optim.4,754–776(1993)

9.Garza,A.D.L.,Darmofal,D.:An all-at-once approach for multidisciplinary design optimization.In:Proceedings of 16th AIAA Applied Aerodynamics Conference,Albuquerque,June 15–18(1998)

10.Allison,J.,Kokkolaras,M.,Papalambros,P.:On the impact of coupling strength on complex system optimization for single-level formulations.In:Proceedings of ASME 2005 International Design Engineering Technical Conferences and Computers and Informa-tion in Engineering Conference,Long Beach,September 24–28(2005)

11.Wujek,B.A.,Renaud,J.E.,Batill,S.M.,et al.:Concurrent subspace optimization using design variable sharing in a distributed computing environment.Concurr.Eng.Res.A 4,361–377(1996)

12.Alexandrov,N.M.,Lewis,R.M.:Analytical and computational aspects of collaborative optimization for multidisciplinary design[J].AIAA J.40,301–309(2002)

13.Sobieszczanskisobieski,J.,Altus,T.D.,Phillips,M.,et al.:Bilevel integrated system synthesis for concurrent and distributed processing.AIAA J.41,1996–2003(2012)

14.Batill,S.,Renaud,J.,Gu,X.:Modeling and simulation uncertainty in multidisciplinary design optimization.In:Proceedings of 8th Symposium on Multidisciplinary Analysis and Optimization,Multidisciplinary Analysis Optimization Conferences,Long Beach,September 6–8(2000)

15.Enevoldsen,I.,Sørensen,J.D.:Reliability-based optimization in structural engineering.Struct.Saf.15,169–196(1994)

16.Wu,Y.-T.,Wang,W.:Efficient probabilistic design by converting reliability constraints to approximately equivalent deterministic constraints.J.Integr.Des.Process Sci.2,13–21(1998)

17.Li,G.,Cheng,G.:Optimal decision for the target value of performance-based structural system reliability.Struct.Multidiscip.Optim.22,261–267(2001)

18.Youn,B.D.,Choi,K.K.:A new response surface methodology for reliability-based design optimization.Comput.Struct.82,241–256(2004)

19.Du,X.,Chen,W.:Sequential optimization and reliability assessment method for efficient probabilistic design.J.Mech.Design 126,871–880(2004)

20.Liang,J.,Mourelatos,Z.P.,Tu,J.:A single-loop method for reliability-based design optimization.Int.J.Prod.Dev.5,76–92(2004)

21.Cheng,G.,Xu,L.,Jiang,L.:A sequential approximate programming strategy for reliability-based structural optimization.Comput.Struct.84,1353–1367(2006)

22.Shan,S.,wang,G.:Reliable space pursuing for reliability-based design optimization with black-box performance functions.Chin.J.Mech.Eng.22,27–35(2009)

23.Sues,R.,Cesare,M.:An innovative framework for reliability-based MDO.In:Proceedings of 4 1st Structures,Structural Dynamics,and Materials Conference and Exhibit,Atlanta,April 3–6(2000)

24.Padmanabhan,D.,Tappeta,R.,Batill,S.:Monte Carlo simulation in reliability based optimization applied to multidisciplinary system design.In:Proceedings of 44th Structures,Structural Dynamics,and Materials Conference,Norfolk,April 7–10(2003)

25.Agarwal,H.,Renaud,J.:Reliability based design optimization using response surfaces in application to multidisciplinary systems.Eng.Optim.36,291–311(2004)

26.Ahn,J.,Kwon,J.H.:An efficient strategy for reliability-based multidisciplinary design optimization using bliss.Struct.Multidiscip.Optim.31,363–372(2006)

27.Du,X.,Guo,J.,Beeram,H.:Sequential optimization and reliability assessment for multidisciplinary systems design.Struct.Multidiscip.Optim.35,117–130(2008)

28.Meng,D.,Li,Y.F.,Huang,H.Z.,et al.:Reliability-based multidisciplinary design optimization using subset simulation analysis and its application in the hydraulic transmission mechanism design.J.Mech.Design 137,051402(2014)

29.Lin,P.T.,Gea,H.C.:Reliability-based multidisciplinary design optimization using probabilistic gradient-based transformation method.J.Mech.Design 135,021001(2013)

30.Xiao,Q.,Sues,R.,Rhodes,G.:Multi-disciplinary wing shape optimization with uncertain parameters.In:Proceedings of 40th Structures,Structural Dynamics,and Materials Conference and Exhibit,St.Louis,April 12–15(1999)

31.Nikbay,M.,Kuru,M.N.:Reliability based multidisciplinary optimization of aeroelastic systems with structural and aerodynamic uncertainties.J.Aircr.50,708–715(2013)

32.Huang,Z.L.,Jiang,C.,Zhou,Y.S.,et al.:An incremental shifting vector approach for reliability-based design optimization.Struct.Multidiscip.Optim.53,523–543(2016)

33.Yi,S.I.,Shin,J.K.,Kim,Y.I.,et al.:Comparison of MDO methods with mathematical examples.Struct.Multidiscip.Optim.35,391–402(2008)

34.Hasofer,A.M.:Exact and invariant second-moment code format.J.Eng.Mech.100,111–121(1974)

35.Rackwitz,R.,Flessler,B.:Structural reliability under combined random load sequences.Comput.Struct.9,489–494(1978)

36.Madsen,H.O.,Krenk,S.,Lind,N.C.:Methods of Structural Safety.Prentice-Hall,Englewood cliffs(1985)

37.Burden,R.L.,Faires,J.D.:Numerical Analysis,4th edn.PWS Publishing Co.,Boston(1988)

38.Kearsley,S.K.:On the orthogonal transformation used for structural comparisons.Acta Crystallogr.A 45,208–210(1989)

39.Brewer,T.:Digital airborne camera:introduction&technology.Soil Use Manage.26,379–379(2010)

40.Fletcher,R.:Practical Methods of Optimization,2nd edn.Wiley-Interscience,New York(1987)

41.Abelein,U.,Lochner,H.,Hahn,D.,et al.:Complexity,quality and robustness–the challenges of tomorrow’s automotive electronics.In:Proceedings of Design,Automation&Test in Europe Conference&Exhibition,Dresden,March 12–16(2012)