Mobile bed thickness in skewed asymmetric oscillatory sheet flows
Xin Chen·Yong Li·Fujun Wang
1 Introduction
Sheet flow happens as an important sediment transport regime when the Shields parameter over a mobile bed is larger than about0.8–1.0,where sediment concentrations are very high and the sediment flux is large.Measurement difficulties exist in the rather thin sheet flow layer with mobile bed thickness from millimeters to centimeters[1],and the actual knowledge is relatively weak in the sheet flow layer compared to the outer layer.The relevant mobile bed thickness is very crucial,because the sediment transport rate is usually obtained by the product of mobile bed thickness and averaged velocity.Both steady and unsteady flow studies about mobile bed thickness have been conducted widely in the recent quarter-century[1–3],and applied in instantaneous sediment transport rate models,but limitations exist,such as suspended sediment,phase-lag effects,and asymmetric boundaries in skewed asymmetric oscillatory flows.Improvement of the instantaneous mobile bed thickness theory is necessary.
A linear relationship between dimensionless mobile bed thickness and the Shields parameter is widely accepted,but suspended sediment is usually not included,which leads to unrealistic constants or even increasing erosion depth with increments of sediment diameter[4].Furthermore,mobile bed thickness is zero near flow reversal when a linear relationship is applied,and the difference between onshore and offshore flows is always absent in asymmetric flows.However,its non-zero mobile bed thickness can be seen when phase-lag is comparatively large[1],along with obvious differences between onshore and offshore flows in asymmetric development of the flow boundary.For accurate prediction of the instantaneous mobile bed thickness in unsteady flows,it is necessary to consider the suspended sediment,phase-lag effects[1,5,6],and asymmetric development of the boundary layer.
Figure 1 shows the typical sediment concentration profile in sheet flows.The mobile bed thickness for sediment transport in sheet flow is represented by erosion depthZand sheet flow layer thicknessδ.The immobile bed surface is com-monly defined to be where the volumetric concentrationSis 0.99Sm,wheremdenotes the maximum value.Erosion depth is commonly defined as the distance between initial still bed level and the top of the immobile bed surface,below which is the immobile layer.Sheet flow layer thickness is defined as the distance between the top of immobile bed surface and the level at whichS=0.08,where averaged particle spacing is almost one particle diameter and particle interactions are negligible,above which is the suspension layer.Previous studies can generally be divided into models referring only to the erosion depth[1,6–8],only to the sheet flow layer thickness[3,5,9,10]or referring to both[4].The relationship between erosion depth and sheet flow layer thickness has not been obtained,even though they both represent the mobile bed thickness.Conflict exists between erosion depth and sheet flow layer thickness[4]without mass conservation in previous studies,so mass conservation[5]must be considered.
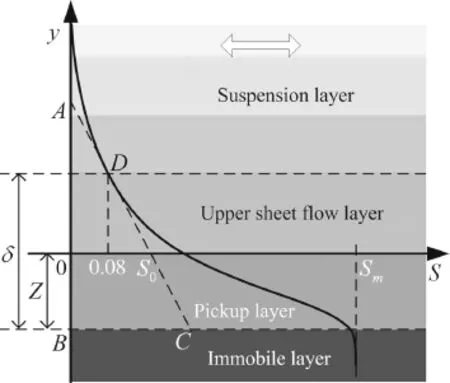
Fig.1 Nearbed concentration profile of oscillatory sheet flow
The present study aims to develop an instantaneous mobile bed thickness model for sediment transport in sheet flow conditions.Special attention is paid to the effects of suspended sediment,mass conservation,phase-lag,and asymmetric boundary development.Finally,the new model is applied to sediment transport rate prediction.In the following,we introduce the new model in Sect.2,and discuss the validity of the new model and its application in sediment transport rate in Sects.3 and 4.After that the conclusions are drawn in Sect.5.
2 New mobile bed thickness model
Defined in Fig.2a,the analytical approximation of skewed asymmetric free steam velocity[11]is
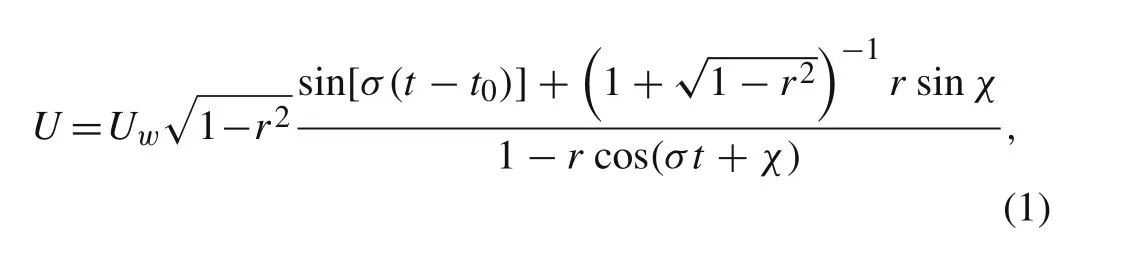

Typical skewed asymmetric flow happens when 0<r<1 and−π/2<χ<0.Otherwise,Eq.(1)reduces to sinusoidal flow whenr=0,to pure velocity-skewed flow whenχ=−π/2 and to pure acceleration-skewed flow whenχ=0 in Fig.2b.
2.1 New erosion depth
The new erosion depth,Z,is derived with the consideration of suspended sediment,phase-lag,and asymmetric boundary development.The erosion depth includes a bed load part Zband suspended load partZ s,which are

Fig.2 Free stream velocity U.a Definition of skewed asymmetric U.b Special flow type

whereτis the shear stress on the immobile bed surface,ρis the water density,sis the sediment specific gravity,gis the gravitational acceleration,θis the sediment internal friction angle,ηis the energy efficiency for suspended sediment transport,andwis the sediment falling velocity[12].The instantaneous Shields parameter is
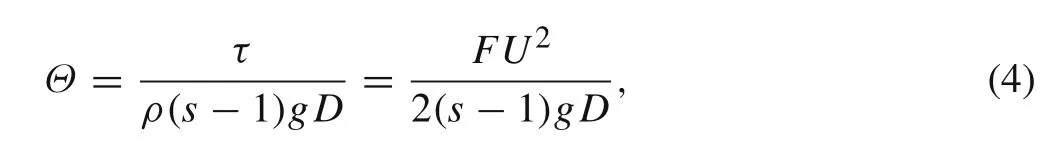
whereDis the sediment diameter,F=(U w f+U0f0)/(U w+U0)is the friction factor for combined wave and current[13],U w=(Uc+Ut)/2,U0is the current velocity,andf0is the current friction factor[13].The wavefis given by Ref.[14]with acceleration modification[3].Considering the asymmetric development of the boundary layer forU,fat the flow peak(U=UcorU=Ut)is given by
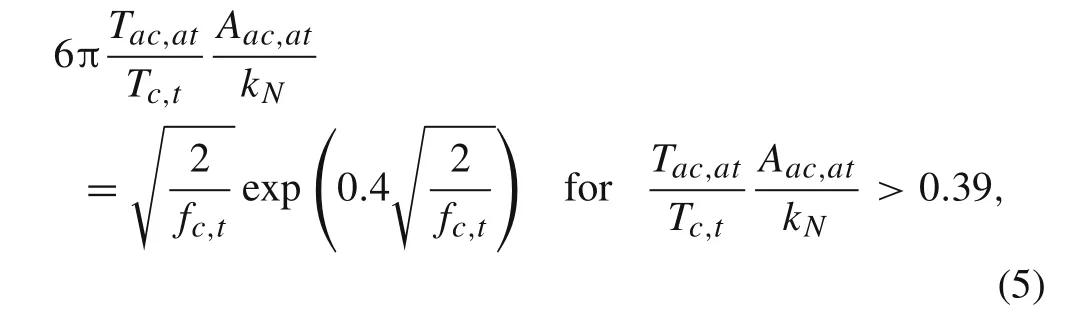
and the flow reversal(U=0)is given with the subscriptabeing replaced bydin Eq.(5);Ais the oscillatory flow orbital amplitude,Aa c,at=2Uc,tTac,a t/π;k N/D=5Θ?1 is the roughness height of mobile bed[14],and iterations are necessary for Eqs.(4)–(5)andkN.InstantaneousAandfare linearly interpolated between flow peak and reversal.
Sensitivity ofSm,η,andθare not focused on here.Instead we take the widely usedSm=0.6 andη=0.02.Averagedθ=28°is simply given by data from[1,4,7,8,15].The total erosion depth is

Considering the phase-lag[1],the instantaneous erosion depth is rewritten based on Eq.(6)

whereβ1andβ2are related to the phase-lag parameterΨ=σ Z m/w,representing the time ratio between sediment falling
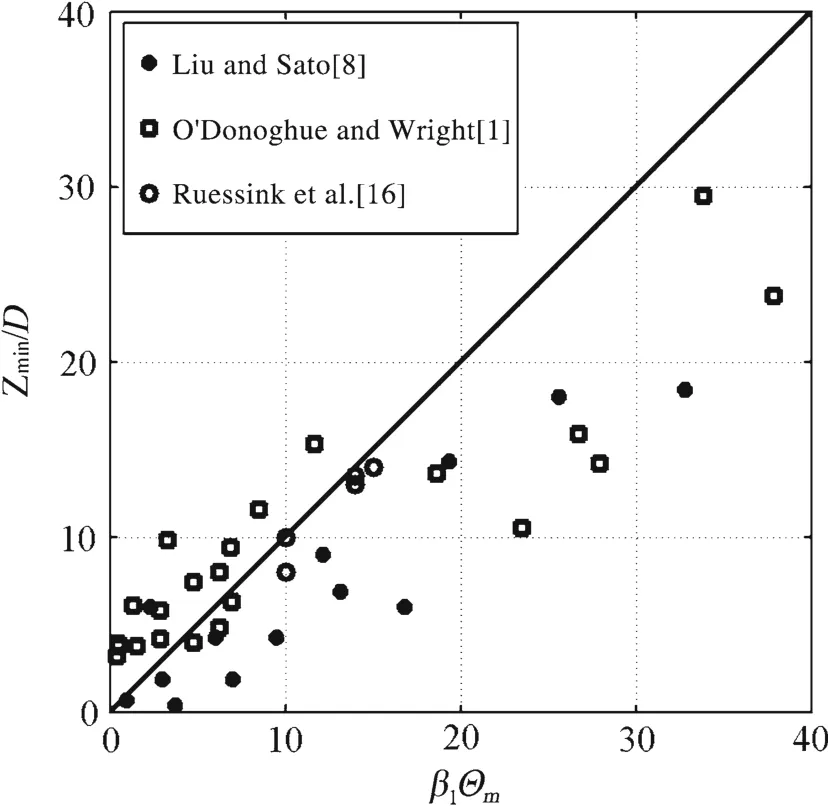
Fig.3 Phase-residual calibration
down and the wave period,Z mis the maximum erosion depth in Eq.(6).Θmis the maximumΘgiven by Eq.(4);β1Θmrepresents the residual sediment amount after flow reversal,andβ1=exp(−0.2/Ψ)is calibrated by the data[1,8,16]in Fig.3,where“Zmin”is the measured minimal erosion depth,β2denotes the variation inZsatisfyingβ1+β2=3.2.
2.2 New sheet flow layer thickness
New sheet flow layer thickness,δ,is obtained by erosion depth due to mass conservation.Considering the mass conservation,the concentration profile is approximated by exponential law or power law[6]
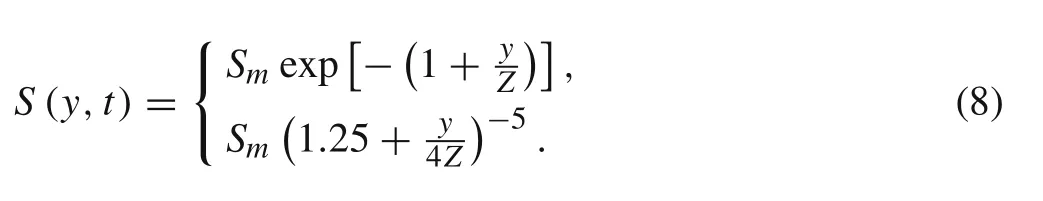
We can derive the top of the sheet flow layery(0.08)=Zby settingS=0.08 andSm=0.6 in Eq.(8).Noticeδ=y(0.08)+Z,thus theδis
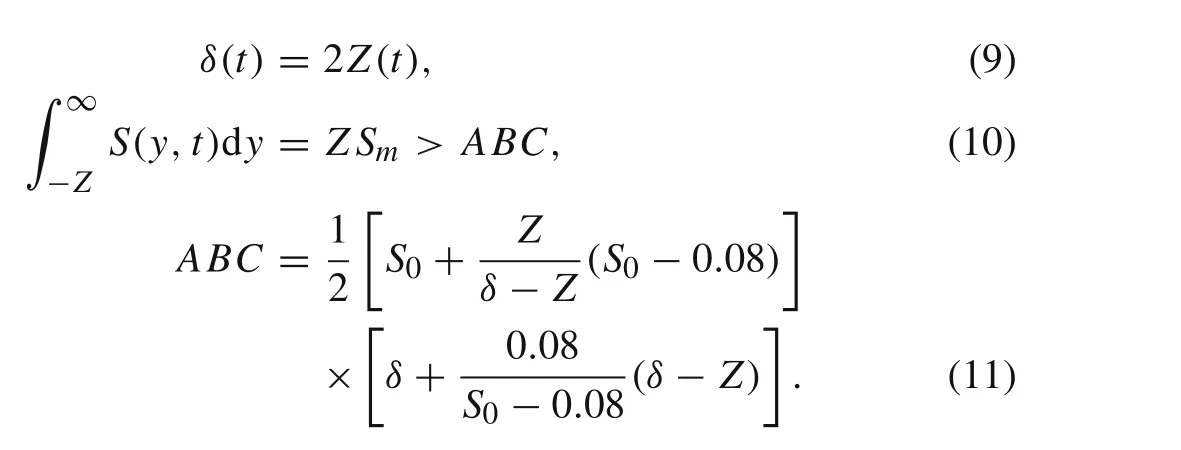
Conservation of sediment mass requires relationship in Eq.(10)with a downward convex profile ofS<0.3,where triangle areaABC,seen in Eq.(11),is the possible minimum eroded sediment amount given byZandδ.Points“A”and“C”are located at theyaxis and the immobile bed surface in Fig 1,and point“B”is the intersection point of theyaxis and the immobile bed surface.ACis a tangent line ofSacross the initial bed withS0,and“D”is the tangent point located at the top of the sheet flow layer.Equations(10)and(11)show a restriction betweenZandδ.Consideration of mass conservation makesZandδin Eq.(9)compatible for most 0.08<S0<0.3,asZ Sm/ABC>1 seen in Fig.4.ButZ/D=7.8Θmandδ/D=35Θmin Ref.[4]do not match each other for case 0.13 mm(Fig.4),whereZ Sm/A B C<1 for every possibleS0.
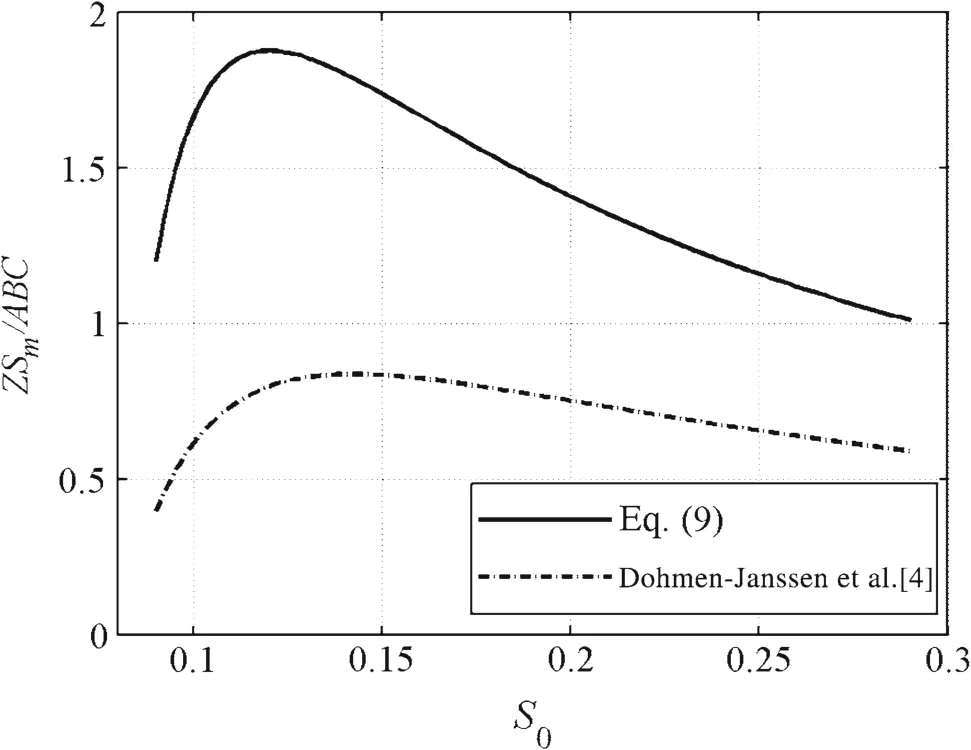
Fig.4 Match performance of Z and δ

Fig.5 Mobile bed thickness comparison
3 Validation of mobile bed thickness
The maximum values(Z/Dandδ/D)are first validated by data in Table 1,which includes the skewed asymmetric flows:pure velocity-skewed flow[1],pure acceleration-skewed flow,and mixed flow].We did not study the characteristic of plug flow[7]when the mobile bed thickness suddenly increases,so data in the range ofσUm/[(s− 1)g]>0.2 are excluded.
Figure 5 is the comparison ofZ/Dandδ/Dbetween present predictions and measurements,where the dash dotted lines represent the two-fold deviation.Measurement uncertainties exist in the rather thin sheet flow layer of millimeters to centimeters[1],and the sensitivity ofSm,η,andθare neglected.However,data ofZ/Dbetween the dash-dotted lines are 94.39%,which reasonably confirms the validity of suspended sediment and asymmetric boundary development in Eq.(6).Meanwhile,the consideration of mass conservation is also reasonable,because 92.52%data ofδ/Dderived from mass conservation are between the twofold deviation lines.
Periodic variation of mobile bed thickness is important to understand the sediment pick-up and fall-down processes.Collected instantaneous data for validation are listed in Table 2,which includes 4 types of flows in Fig.2b.Respecting the authors,Uis given by Eq.(1)for sinusoidal flow(W36 and LS1),pure acceleration-skewed flow(A1 and A3)and mixed flow(C1),andU=1.2cos[2π(t/T−0.214)]+0.3cos[4π(t/T−0.214)]in pure velocity-skewed flow(FA7515–MA5010).
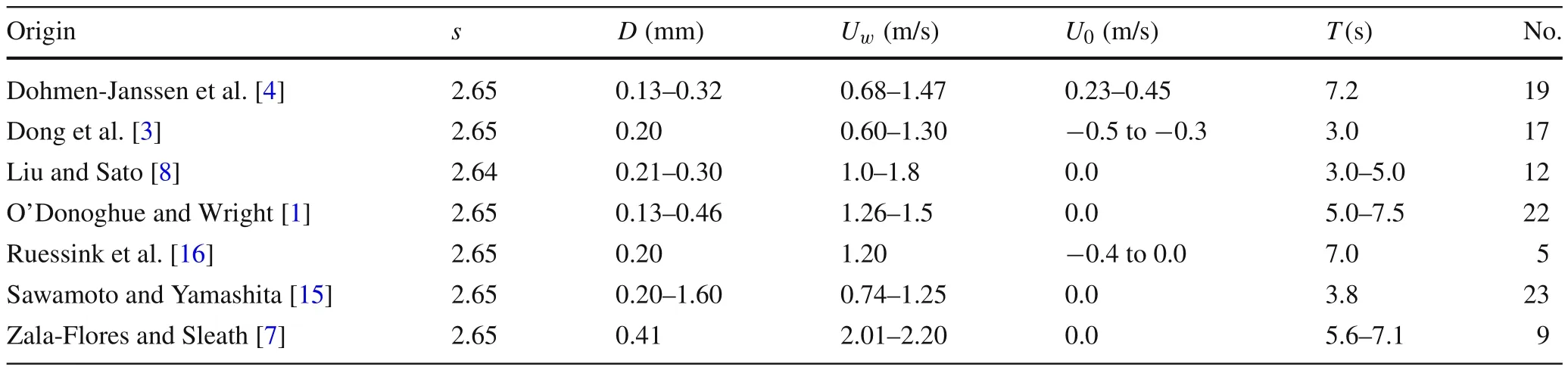
Table 1 Cases for mobile bed thickness validation

Table 2 Cases for instantaneous sediment transport validation
The instantaneous mobile bed thickness comparison between present predictions(Pred.)and measurements(Meas.)is shown in Fig.6,where the bottom and top lines,respectively,correspond to the immobile bed surface(−Z)and the top of the sheet flow layer[y(0.08)=Z]in Fig.1.Reasonably good agreement between present predictions and measurements confirms the validity of a phase-residual ofβ1Θmand a phase-shift ofΨin Eq.(7).Again,classicalZ/Z m=Θ/Θm[2,7]is not valid in oscillatory sheet flow due to the phase-lag.For example,in pure velocity skewed flows,Z t/Z c=0.90(Fig.6b)is much larger thanΘt/Θc=0.36(Fig.2b);this is also true in mixed flows(Fig.6f).The minimalZis not 0,even thoughΘ=0,because phase-residual exists,and it occurs a phase-shift aftert/T=0.In sinusoidal flow(Fig.6a),the mobile bed thickness is symmetric betweent/T=0−0.5 andt/T=0.5−1.In pure acceleration-skewed flow(Fig.6d–e),maximumZnear the flow crest(t/T=0.2−0.3)is larger than that near the flow trough(t/T=0.8−0.9)evenUc=Ut,because the acceleration skewness leads to a shear stress near the flow crest larger than that near the flow trough].The effect is considered in Eq.(5),so present predictions can well recognize the difference.Without loss of generality,data of W36,FA5010,and MA5010 are not shown in this section.Instead,their sediment transport rate results are studied in Sect.4.
4 Sediment transport rate
Equation(7)provides a solid foundation for developing a unified and summarized instantaneous formula for sediment transport in skewed asymmetric flows.According to Wilson[19],the velocity at the top of the sheet flow layer is found at about 8.2u∗.With the averaged sediment velocity being about half its value,the dimensionless sediment transport rate formula is
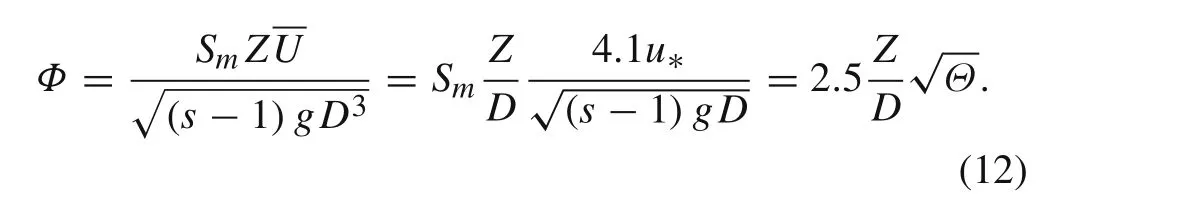

In unsteady flow,the instantaneousΦis usually approximated by Sign(U)|U/Um|n.Various velocity power function exponentsn=1−3 can be unified and summarised in the present study by neglecting phase-shift:ndecreases as the phase-residualβ1increases(Fig.8a).If the phase-lag is as small asβ1=0,Eq.(7)reduces toZ∝U2,and Eq.(12)becomes
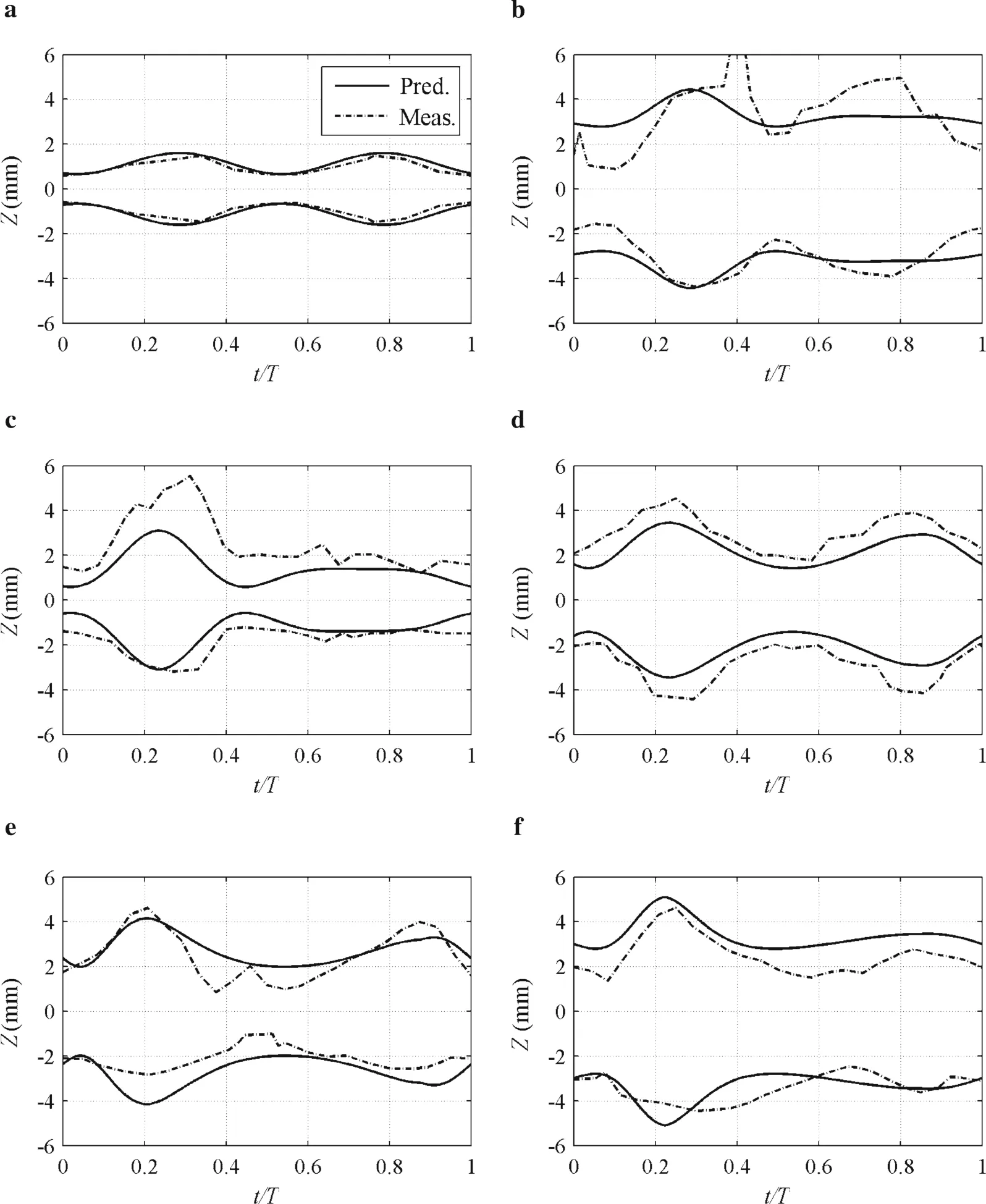
Fig.6 Instantaneous erosion depth and sheet flow layer.a LS1.b FA7515.c MA7515.d A1.e A3.f C1

Table 3 Data for sediment transport rate validation in steady flows
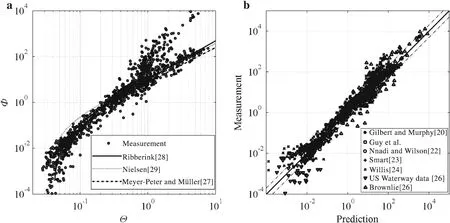
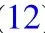
Fig.7 Sediment transport rate in steady flow.a Φ Against Θ .b Prediction by Eq.(12)

Table 4 Sediment transport rate errors in steady flows

Thus,n=3(Fig.8a),which is in agreement with classical instantaneous formulas.If the phase-lag is extremely large,such thatβ1=3.2,the periodicZin Eq.(7)is constant,and Eq.(12)becomes

n=1(Fig.8a).Equation(14)agrees with the large phase-lag cases[1,2].Furthermore,n=2 can be used for approximation of Eq.(12)whenβ1=1.3(Fig.8a).Other studies,such as W36 in Fig.8b,1.3<β1=1.86<3.2,andn=1.7 is calibrated in agreement with Trow bridge and Young[30].In Figs.8b and 9,the result ofn=1(dashes-dotted)also represents the free streamU;n=3(dashed line)represents classical instantaneous formulas;Nielsen[29](dotted line)represents the bed load formulas.
In previous studies,most of the formulas are invalid for instantaneous sediment transport rate in skewed asymmetric flow.Figureshows the instantaneous sediment transport rates in pure velocity-skewed flow(Table 2),where only Eq.(12)fits all cases.Nielsen[29]bed load formula always underestimates the results without the suspended sediment,and classical instantaneous formulan=3 fails at the flow trough(t/T=0.5−0.9)when phase-residual is obvious withβ1=2.65 and 2.28(Fig.9a,b).Due to the phase-shiftΨin erosion depth,the maximumΦin the present model is not located att/T=0.214 whenUis maximal,and Eq.(12)is very close ton=1,even thoughβ1=2.65<3.2 in Fig.9a.Since the sediment transport rate is a product of mobile bed thickness,the good agreement between Eq.(12)and the measurements again confirms the validity of instantaneous Eq.(7).However,the periodic integration of Eq.(12)is still not enough for net sediment transport rate in skewed asymmetric flow,because the net current generated by skewed asymmetric flow[1,18]has not been presented,and net current would generate an extra net sediment transport rate.
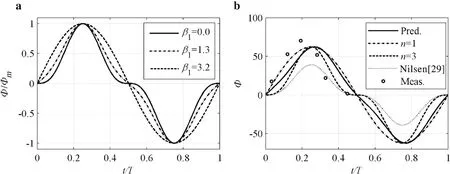
Fig.8 Instantaneous sediment transport in sinusoidal flow a Velocity exponents n and β1.b W36,β1=1.86

Fig.9 Instantaneous sediment transport rate in 2nd Stokes flow.a FA5010,β1=2.65.b FA7515.β1=2.28.c MA5010.β1=1.25.d MA7515.β1=0.60
5 Conclusions
This paper develops a new instantaneous mobile bed thickness model for skewed asymmetric oscillatory sheet flows,and derives the relationship between erosion depth and sheet flow layer thickness,both of which represent the mobile bed thickness.The new model is validated by data covering a wide range of sediment diameters,periods, flow strengths and types.Comprehensive consideration of suspended sediment,mass conservation,phase-lag,and asymmetric boundary layer development ensures the model accuracy.In addition,an instantaneous sediment transport formula is obtained based on the new mobile bed thickness model in skewed asymmetric flows.The instantaneous sediment transport rate proportional to various velocity power function exponents 1–3 are unified and summarised by neglecting phase-shift,i.e.,the exponent decreases as the phase-residual increases.
AcknowledgementsThe project was supported by the National Natural Science Foundation of China(Grants 51609244,11472156,and 51139007)and the National Science-Technology Support Plan of China(Grant 2015BAD20B01)
1.O’Donoghue,T.,Wright,S.:Concentrations in oscillatory sheet flow for well sorted and graded sands.Coast.Eng.50,117–138(2004)
2.Dick,J.E.,Sleath,J.F.A.:Sediment transport in oscillatory sheet flow.J.Geophys.Res.97,5745–5758(1992)
3.Dong,L.,Sato,S.,Liu,H.:A sheet flow sediment transport model for skewed-asymmetric waves combined with strong opposite currents.Coast.Eng.71,87–101(2013)
4.Dohmen-Janssen,C.M.,Hassan,W.N.,Ribberink,J.S.:Mobilebed effects in oscillatory sheet flow.J.Geophys.Res.106,103–115(2001)
5.Malarkey,J.,Pan,S.,Li,M.,et al.:Modelling and observation of oscillatory sheet-flow sediment transport.Ocean Eng.36,873–890(2009)
6.Chen,X.,Niu,X.,Yu,X.:Near-bed sediment condition in oscillatory sheet flows.J.Waterw.Port.Coast.Ocean.Eng.139,393–403(2013)
7.Zala-Flores,N.,Sleath,J.:Mobile layer in oscillatory sheet flow.J.Geophys.Res.103,12783–12793(1998)
8.Liu,H.,Sato,S.:Laboratory study on sheet flow sediment movement in the oscillatory turbulent boundary layer based on image analysis.Coast.Eng.J.47,21–40(2005)
9.Wilson,K.C.:Analysis of bed-load motion at high shear stress.J.Hydraul.Eng.ASCE.113,97–103(1987)
10.Sumer,B.M.,Kozakiewicz,A.,Fredsøe,J.,etal.:Velocity and concentration profiles in sheet-flow layer of movable bed.J.Hydraul.Eng.ASCE.122,549–558(1996)
11.Abreu,T.,Silva,P.A.,Sancho,F.,et al.:Analytical approximate wave form for asymmetric waves.Coast.Eng.57,656–667(2010)
12.van Rijn,L.C.:Principles of Sediment Transport in Rivers,Estuaries and Coastal Seas.Aqua Publications,Blokzijl(1993)
13.Madsen,O.,Grant,W.:Sediment transport in the coastal environment.Technical Report 209,M.I.T.,Cambridge,Massachusetts,USA(1976)
14.Wilson,K.C.,Andersen,J.S.,Shaw,J.K.:Effects of wave asymmetry on sheet flow.Coast.Eng.25,191–204(1995)
15.Sawamoto,M.,Yamashita,T.:Sediment transport rate due to wave action.J.Hydrosc.Hydraul.Eng.4,1–15(1986)
16.Ruessink,B.G.,Michallet,H.,Abreu,T.,et al.:Observations of velocities,sand concentrations,and fluxes under velocity a symmetric oscillatory flows.J.Geophys.Res.Oceans.116,C03004(2011)
17.van der Zanden,J.,Alsina,J.M.,Cáceres,I.,et al.:Bed level motions and sheet flow processes in the swash zone:observations with a new conductivity-based concentration measuring technique(CCM+).Coast.Eng.105,47–65(2015)
18.Yuan,J.,Madsen,O.S.:Experimental and theoretical study of wave-current turbulent boundary layers.J.Fluid.Mech.765,480–523(2015)
19.Wilson,K.C.:Analysis of contact-load distribution and application to deposition limit in horizontal pipes.J.Pipelines.4,171–176(1984)
20.Gilbert,G.K.,Murphy E.C.:The transportation of debris by running water.Technical Report 86,U.S.Geological Survey(1914)
21.Guy,H.P.,Simons,D.B.,Richardson,E.V.:Summary of alluvial channel data from flume experiments.J.Biol.Chem.283,5148–5157(1966)
22.Nnadi,F.N.,Wilson,K.C.:Motion of contact-load particles at high shear stress.J.Hydrol.Eng.118,1670–1684(1992)
23.Smart,G.:Sediment transport formula for steep channels.J.Hydraul.Eng.ASCE.111,267–276(1984)
24.Willis,J.C.,Coleman,N.L.,Ellis,W.M.:Laboratory study of transport of fine sand.J.Hydraul.Div.ASCE.98,489–501(1972)
25.Willis,J.C.:Suspended load from error-function models.J.Hydraul.Div.ASCE.105(7),801–816(1979)
26.Brownlie,W.:Compilation of alluvial channel data:laboratory and field.Technical Report KH-R-43B,California Institute of Technology,Pasadena(1981)
27.Meyer-Peter,E.,Müller,R.:Formulas for bed-load transport.In:Report on the 2nd Meeting International Association Hydraulic Structure Research,Stockholm(1948)
28.Ribberink,J.S.:Bed-load transport for steady flows and unsteady oscillatory flows.Coast.Eng.34,59–82(1998)
29.Nielsen,P.:Sheet flow sediment transport under waves with acceleration skewed and boundary layer streaming.Coast.Eng.53(9),749–758(2006)
30.Trowbridge,J.,Young,D.:Sand transport by unbroken water waves under sheet flow conditions.J.Geophys.Res.94,10971–10991(1989)
- Acta Mechanica Sinica的其它文章
- Measurement of the flow structures in the wakes of different types of parachute canopies
- Effect of perforation on flow past a conic cylinder at Re=100:vortex-shedding pattern and force history
- Mechanical properties of gas hydrate-bearing sediments during hydrate dissociation
- A modified multi-objective particle swarm optimization approach and its application to the design of a deep water composite riser
- Reliability-based multidisciplinary design optimization using incremental shifting vector strategy and its application in electronic product design
- Time-varying nonlinear dynamics of a deploying piezoelectric laminated composite plate under aerodynamic force

