Maple软件的动态可视化功能在大学数学教学中的应用探索

孔祥强，刘秀英

（菏泽学院 数学与统计学院，山东 菏泽 274015）

0 引言

Maple软件作为重要的数学类软件，不仅具有较强的符号计算功能和数值计算功能，而且具有强大的动态绘图功能［1］。其动态绘画功能使得图形的绘制具有可视化的效果，因而已广泛应用于数学的各大分支［2-6］。由于大学数学课程内容比较抽象，部分概念较难理解，某些函数的图像也很难手工完成，因此为了使学生更好地掌握大学数学的内容，提高学习的积极性，在课堂上应用Maple软件的动画作图功能是十分必要的。本文重点从3个方面探讨了Maple软件在大学数学中的具体应用。

1 平面图形动态作图的可视化效果

在同一坐标系下，依据Maple软件可同时作出函数及其各阶导数的动态图，从而可更好地理解函数的一系列性质，如单调性、凹凸性、极值和最值等［7］。通过单击动画播放的“开始／继续”按钮调节播放的进度，通过“前一帧”“下一帧”按钮控制动画的输出。动画可自动播放，也可手动控制。

1.1 直角坐标系下函数及其一阶、二阶导数的动态作图应用

例1 作出函数y=0.4x+2cosx，x∈[0,7]的图像，并在同一坐标系中作出其一阶、二阶导数的图形。利用Maple软件编程，源代码如下：

在所得图像上单击鼠标右键，选择“动画”，根据其下拉菜单即可选择“播放”“加速播放”“减速播放”“向前”“向后”等不同的动画播放方式。当帧数为100时，所得图像见图1；当帧数为200时，所得图像见图2。

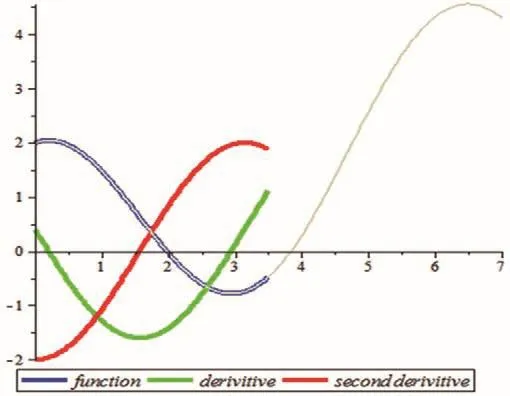
图1 函数及其导数的部分图Fig.1 Partial figure of function and its derivative

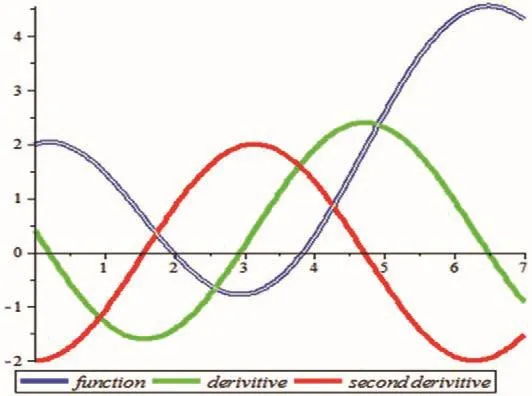
图2 函数及其导数的整体图Fig.2 Whole figure of function and its derivative

1.2 极坐标系下函数的动态作图应用

极坐标系下常见的曲线如对数螺线、双纽线、玫瑰线、旋轮线等，用手工作图很难完成，为了更直观、更高效地学习曲线的生成过程，借助Maple软件很容易达到目的［8］。

例2 作出等速螺线ρ=aθ的动态图。利用Maple软件编程，源代码如下：

程序中给出了两个不同颜色的等速螺线图形。取帧数为44时，所得动态图见图3；帧数为87时，所得动态图见图4。

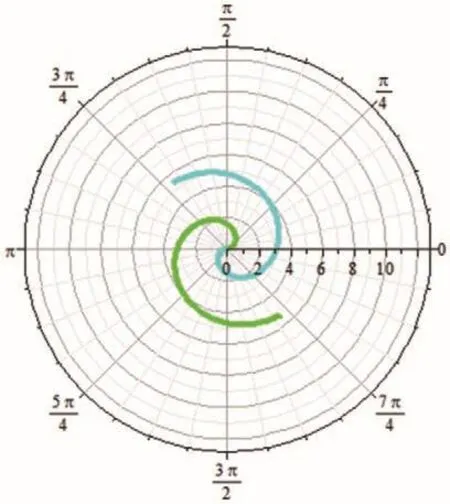
图3 等速螺线的部分图Fig.3 Partial figure of uniform speed spiral

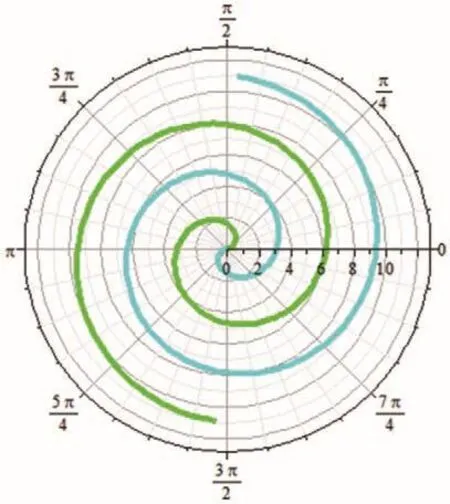
图4 等速螺线的整体图Fig.4 Whole figure of uniform speed spiral

2 空间图形的动态可视化效果

空间中的曲线、曲面及空间立体图形的描绘是大学数学中的难点，为了更好地掌握这部分内容，可充分利用Maple软件作图的动画功能，并且可选择不同的视角对图形进行深入的观察，也可添加图形的辅助效果等，从而锻炼学生的空间逻辑思维能力，提高学习的效率。

2.1 空间立体图形动态作图的应用

例3 作出由θ=β和r=2acosβ所围成的动态球顶锥体，其中的参数a在具体作图时可以取不同的值,如取a=2时，由Maple软件编程，源代码如下：

帧数为36时，所得图形见图5；帧数为63时，所得图形见图6。当半顶角发生变化时，便可得到不同的球顶锥体,图5和图6是半顶角为两个特殊值时的立体图形。

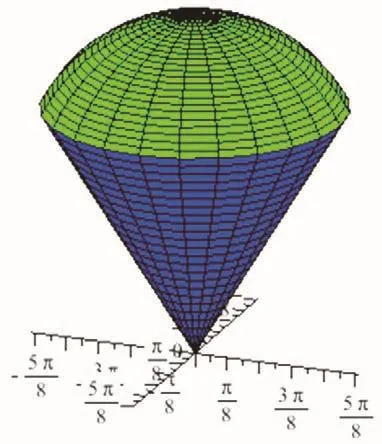
图5 球顶锥体1Fig.5 The first spheroid pyramid graph

图6 球顶椎体2Fig.6 The second spheroid pyramid graph

同时，在图形上单击鼠标左键，可任意旋转立体图形，从不同的视角全方位了解所作的图形；单击右键，选择“光泽度”“照明”“颜色”等，可得到不同的图形效果，若选择“样式”下拉菜单中的“带等高线的曲面”，则可为图形添加等高线。图形的透视化效果也可轻松实现。因此，可根据实际情况需要，做出恰当的选择。

2.2 空间曲面图形动态作图的应用

利用Maple软件，可动态化地作出空间旋转曲面，如旋转椭球面、旋转抛物面、旋转双曲面等［8］；也可作出用平面截曲面所得截口的动态效果图；还可根据题目需要，作出具有特殊效果的部分或整体空间曲面。

例4 作出由x=q,y=q,z=3q绕z轴旋转所得旋转单叶双曲面的动态图，且图像具有“跳动”的效果。由Maple软件编程，源代码如下：

利用上面程序display语句中的3*floor（i∕3），即每3帧变化1次，便可实现图形的跳动效果。帧数为37时，所得图形见图7；帧数为98时，所得图形见图8。

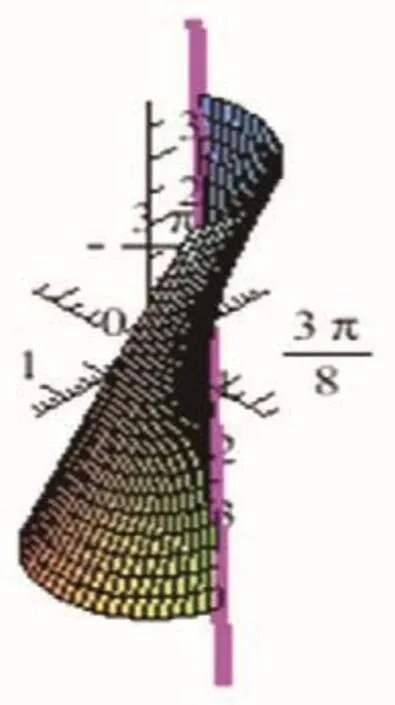
图7 带有直纹的单叶双曲面部分图Fig.7 Partial figure of single-leaf hyperboloid with straight lines

图8 带有直纹的单叶双曲面整体图Fig.8 Whole figure of single-leaf hyperboloid with straight lines

对于动态图形，可用“连环画”的形式输出各帧的图像，以便更好地了解图形产生的过程。

上面程序的输出结果为“连环画”形式，由于程序中T值为4，所以输出为4帧图画，见图9。

图9 单叶双曲面的“连环画”输出Fig.9 Dynamic output of single-leaf hyperboloid

3 利用软件动态解释数学中的抽象定义

对数学概念的准确把握是学好数学的关键，Maple的可视化功能将抽象的问题具体化、复杂的问题简单化，从而达到正确理解概念的目的。以定积分的定义为例进行说明。

定积分的定义可以用“分割、近似、求和、取极限”四步概括，最关键的步骤是“近似”过程，体现了“以直代曲”的数学思想，即用小矩形的面积近似代替小曲边梯形的面积。矩形的高可以用区间左端点处的函数值代替，也可用区间右端点处的函数值代替，还可用区间中点处的函数值代替。本文利用Maple软件编程动态可视化地展现这一过程。

例5 对函数y=x2-x，动态展示其在区间［-1，2］上的黎曼和。

1）以区间左端点处的函数值代替矩形的高，帧数为20时动态图见图10。

2）以区间中点处的函数值代替矩形的高，帧数为23时动态图见图11。

3）以区间右端点处的函数值代替矩形的高，帧数为26时动态图见图12。

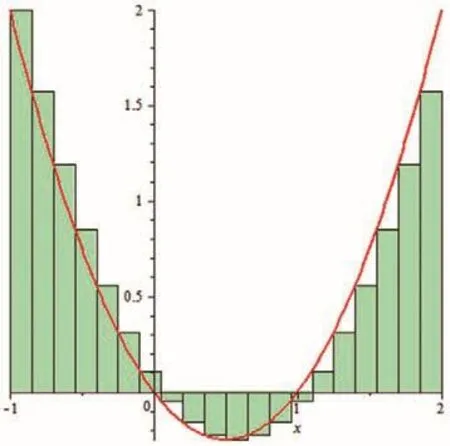
图10 左端点处的函数值为高时的动态图Fig.10 Dynamic graph of function value as high at the left endpoint

图11 区间中点处函数值为高时的动态图Fig.11 Dynamic graph of function value as high at the midpoint of the interval

图12 右端点处的函数值为高时的动态图Fig.12 Dynamic graph of function value as high at the right endpoint

4 讨论

在Maple软件中，可利用编程实现动态作图，如用plot3d（）函数等；也可利用交互式绘制器Plot Builder绘制图形。利用Maple提供的对象函数可实现空间曲面的变位变形动画；利用变换函数、绘图函数可实现步进踪迹动画，匀步长和变步长均可；绘图函数结合display（）函数可绘制动态的曲线图，通过控制参数达到控制整个动画的目的。以Maple软件为依托，大学数学中与空间图形有关的知识难点均可得到可视化的展现。除了本文所讨论的几个方面，Maple软件的动态可视化功能在重积分、线面积分等方面也有很好的应用［10］。将数学软件和传统的教学方式结合起来，使学生更容易理解晦涩的数学概念和定理，多种教学手段并用更能激发学生的兴趣和潜能，同时也提高了教学质量和效率，很大程度上培养了学生的探索能力和创新能力。

参考文献（References）

［1］ 张晓丹，堵秀凤，李祥林，等.Maple的图形动画技术［M］.北京：北京航空航天大学出版社，2005.

［2］ 李静，腾兴虎.Maple软件在高等数学中的应用［J］.大学数学，2014，30（S1）：95-97.

［3］ 李姝妹.数学软件Maple在常微分方程教学中的应用［J］.阴山学刊，2013，27（4）：55-57.

［4］ 额尔敦布和，白秀，王海清.Maple软件在数学分析教学中的应用研究［J］.内蒙古民族大学学报（自然科学版），2013，28（2）：146-149.

［5］ 李银，位瑞英.基于Maple软件《常微分方程》一体化教学的探讨［J］.韶关学院学报，2016，37（12）：73-77.

［6］ 曹建莉，刘媛媛，赵梦亚.一类孤立子方程的Maple软件求解［J］.数理化研究，2015（8）：287.

［7］ 科罗夫斯基威茨·瑞伊.微积分：Maple实验教程［M］.北京：机械工业出版社，2008.

［8］ 孔祥强.Maple软件在大学数学教学中的应用［J］.赤峰学院学报，2016，32（2）：6-8.

［9］ 孔祥强.Maple在高等数学教学中的应用探索［J］.钦州学院学报，2016，31（1）：54-57.

［10］王剑侠，龚力强，万丽.Maple在重积分教学中的应用［J］.工科数学，2002，18（6）：38-40.