Parameters Sensitivity Analysis and Correction for Concrete Damage Plastic Model
Yaqin Jiang, Pengfei Xu, Chengzhi Wang and Dianshu Liu
(1.School of Mechanics and Civil Engineering, China University of Mining and Technology, Beijing 100083,China; 2.College of Civil Engineering and Architecture, Henan University of Technology, Zhengzhou 450001, China; 3.School of Materials Science and Engineering, Beijing Institute of Technology, Beijing 100081, China)
Currently,many concrete models have been established to simulate nonlinear responses, which include Geological Damage (MAT25), Concrete Damage Rel3(MAT72R3), Winfrith Concrete(MAT84), Johnson Holmquist Concrete (MAT111), Schwer Murray Cap (MAT145), CSCM Concrete (MAT159) and RHT (MAT272)[1]. Most models are based on plasticity mechanism, damage mechanism, or combination of plasticity and damage[2]. Plasticity models fail to describe stiffness degradation during unloading tests, while isotropic damage models can describe irreversible deformations in experiments. In 2006, Grassl[3]et al. introduced a damage-plastic model for concrete, which combined plastic effective stress and isotropic damage. The plastic part adopts a strength envelope yield surface proposed by Menetrey and Willam[4]. The damage part employs tensile damage variables and compressive principal stress state proposed by Ortiz[5].
Then LS-DYNA material library added a damage plastic concrete model based on the work of Grassl et al. These model parameters are mainly classified into three categories, which control elastic phase, hardening phase and softening phase of the stress-strain curve, respectively. Most of them have default values from experimental tests[1]. Hardening ductility parameters AH, BH, CH, DH control the hardening phase, while the damage softening phase is controlled by the damage ductility parameter AS and damage ductility exponent BS. However, the effect of these parameters on the mechanical responses of concrete is still not clear[3, 6-7]. Moreover, it is complicated to directly obtain these parameters through experiments, and the sensitivity and reliability of nonlinear finite element analysis is not only determined by the corresponding nonlinear model, parameter setting, but affected by the unit size[8].
Therefore, herein a cube unit testing through the LS-DYNA finite element software was conducted to analyze the sensitivity of the hardening and softening ductility parameters, and correction of these parameters was eventually made. The study can provide a reliable reference and basis for the concrete structural analysis using the concrete damage plastic model.
1 Concrete Damage Plastic Model
The parameters[1]of the concrete damage plastic model are listed in Tab.1.

Tab.1 Damage plastic concrete model parameters
Hereρis the mass density;Eis Young’s modulus;υis the Poisson’s ratio;ftis the uniaxial tensile strength (stress);fcis the uniaxial compression strength (stress); HP is the hardening parameter; QH0is the initial hardening defined asfc0/fc, wherefc0is the compressive stress at which the intimal yield surface is reached. AH, BH, CH, DH are hardening ductility parameters 1,2,3,4, respectively; AS is the ductility parameter during damage; BS is the damage ductility exponent during damage; STRFL is the strain rate flag. EQ.1.0 is the strain rate dependent. EQ.0 is no strain rate dependency.
The stress-strain relation for the concrete damage plastic model is
(1)
(2)
where Deis the elastic stiffness;εis the total strain;εpis the plastic strain.
The plasticity model of the present model is based on effective stress, described by the yield function, the flow rule, the evolution law for the hardening variable and the loading-unloading conditions.
The yield function is formulated as
(3)
whereqh1(κp) andqh2(κp) are dimensionless functions that determine the size and shape of the yield surface.
The flow rule is expressed as
(4)
The loading-unloading conditions:
(5)
The damage model of this model is described by the damage loading function, the evolution law for the damage variable, and the loading-unloading conditions. The damage model is described by
(6)
(7)
ω=gd(κd,κd1,κd2)
(8)
2 Sensitivity Analysis

Fig.2 Relationship between peak strength strain of concrete and hardening parameter AH, BH, CH, DH under uniaxial tension, uniaxial compression, and triaxial compression, respectively
In order to understand the effect of hardening and softening ductility parameters on the concrete mechanical response, it is necessary to conduct a parameter sensitivity analysis. The cube unit testing method was employed to conduct numerical simulations in three different loading conditions. The sensitivity of AH, BH, CH, DH and AS, BS was analyzed under uniaxial tension, uniaxial compression, triaxial compression, respectively. The cube unit size is 150 mm×150 mm×150 mm. The unit test boundary constraint condition is shown in Fig.1.
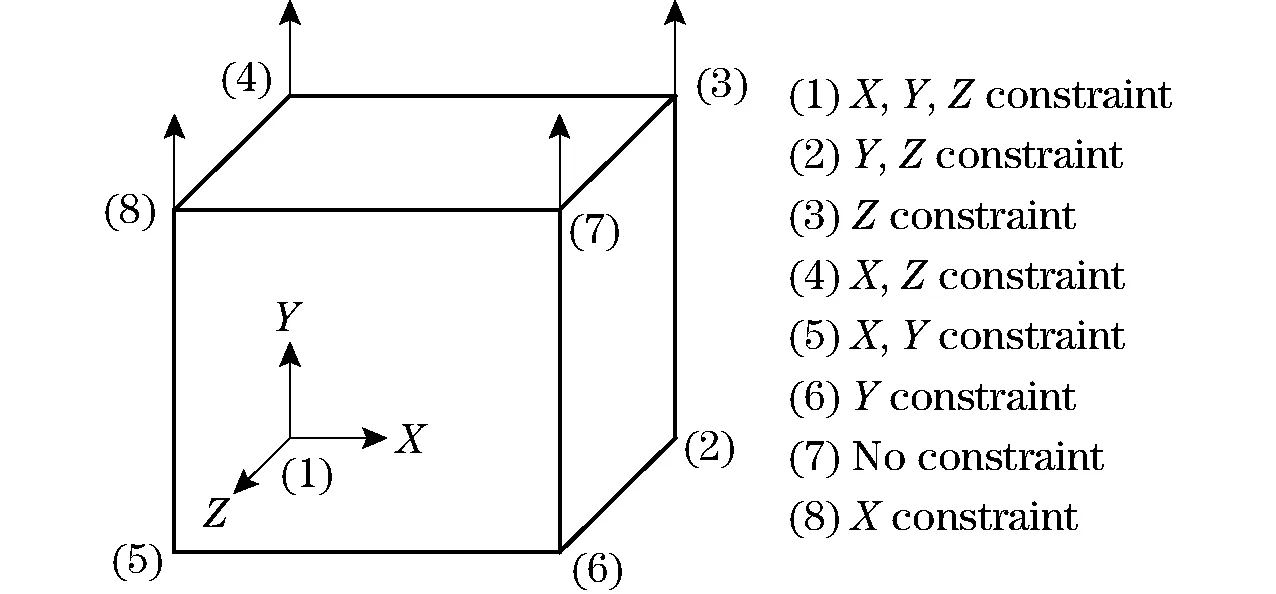
Fig.1 Unit test boundary constraints condition
2.1 Hardening ductility parameters sensitivity analysis
According to the work of Grassal et al., hardening ductility parameters control hardening phase of concrete stress-strain curve. To analyze the sensitivity, the peak strength strain under three load conditions was tested against the hardening ductility parameters AH, BH, CH, DH, respectively.It was shown in Fig. 2 that the peak strength strain was sensitive to AH, BH, CH, but independent of DH under three load conditions. Under the uniaxial tension load, the peak strength strain decreased sharply at lower AH values, rapidly increased at higher BH and CH values. Under the uniaxial compression load, the peak strength strain linearly decreased with AH, and linearly increased with BH and CH. Under the triaxial compression, the peak strength strain linearly climbed up with AH and BH, but nonlinearly decreased with CH.
2.2 Softening ductility parameters sensitivity analysis
In LS-DYNA, the softening phase of the concrete stress-strain curve was controlled by the softening ductility parameter AS and the softening ductility exponent BS. Herein, a softening modulus was used to reflect concrete softening ductility and calculated by the concrete stress, strain at peak strength and the stress, strain as peak intensity dropping 15%. The softening modulus was collected with different AS, BS values to analyze the sensitivity under three load conditions. The relation between the softening modulus and AS, BS was presented in Fig. 3. It can be seen in Fig. 3a that, only under the uniaxial compression and triaxial compression load, the softening modulus nonlinearly decreased with AS. Under the uniaxial tension load, AS has no effect on the softening modulus. As shown in Fig. 3b, the softening modulus is independent of BS in three load cases.

Fig.3 Relationship between softening modulus and softening parameter AS and BS under uniaxial tension, uniaxial compression, and triaxial compression, respectively
3 Model Parameters Correction and Verification
3.1 Model parameters correction
According to the designing code of concrete structures[9], the concrete stress-strain curve in the uniaxial compression is expressed by the following formulas:
σ=(1-dc)Ecε
(9)
(10)
(11)
(12)
(13)
wheredcis the damage evolution parameter in the uniaxial compression;αcis the decreasing phase parameter value of the stress-strain curve in compression;fc,ris the representative value of the uniaxial compressive strength;εc,ris the peak strength strain.
In the case of C30 concrete, the uniaxial compressive stress-strain curve was simulated by the model with default parameters and optimized parameters, respectively. As shown in Fig. 4, the curve simulated by the default model was in good accordance with the standard curve by concrete code model in elastic phase, but exhibited slight difference in hardening phase. In soften phase, the compressive strength simulated by the default model was much higher than that by the code model, which indicated the failure of default parameter model in describing the soften phase in the concrete stress-strain curve. Considering the result in Fig. 3, the softening phase was mainly affected by the softening ductility parameter AS and independent of the softening ductility exponent BS in the uniaxial compression. An optimized model was developed by adjusting the value of AS. Compared with the default mode (AS=15), the optimized model with AS=2 exhibited good consistence with the standard code model in the softening phase. Thus, the simple optimized model with AS correction could be used for accurate prediction of concrete stress-strain curves.
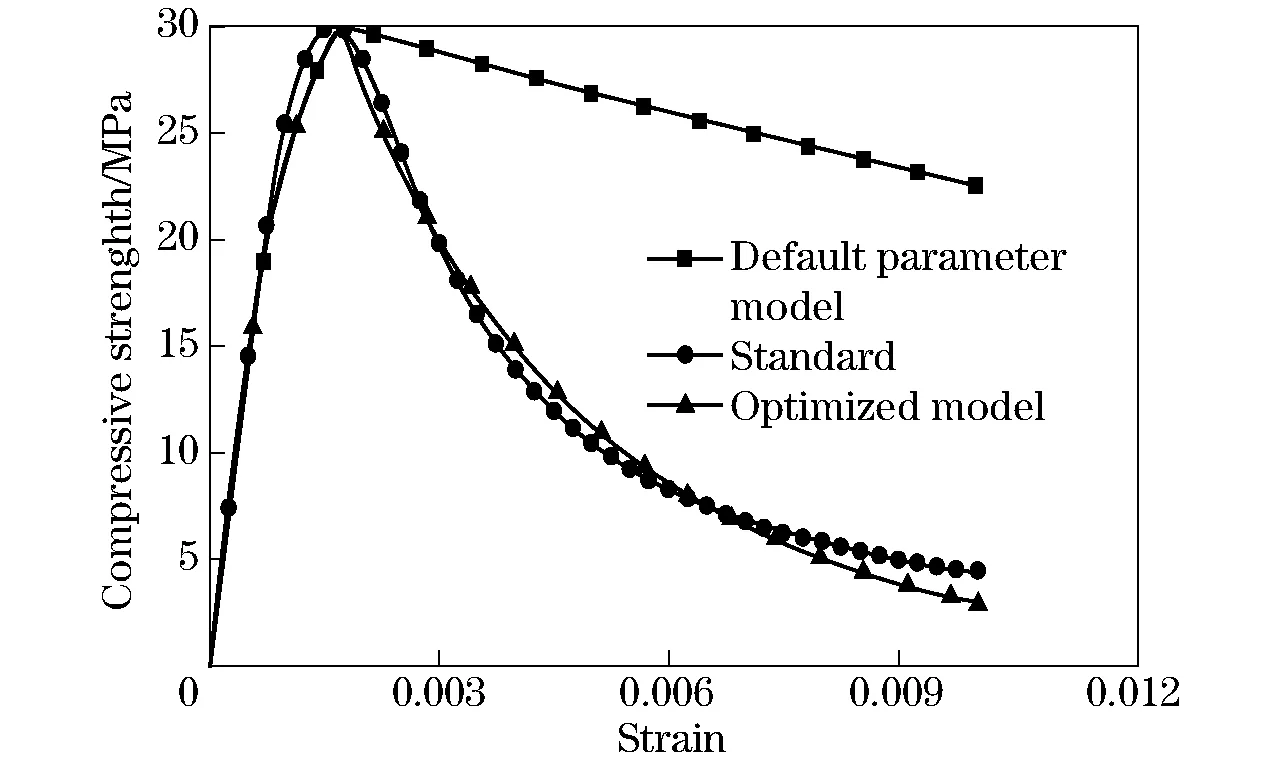
Fig.4 Strain-compressive strength curves simulated by the model with default parameter values, the optimized model with parameter correction, and the standard code model
3.2 Verification
To verify the feasibility of the model with AS correction, the stress-strain curves of concrete with different grades were compared between the code model and the corrected model. As shown in Fig. 5, the corrected model could describe the stress-strain curves of each grade concrete well , only exhibiting slightly higher compressive strength in softening phase for C60 concrete. Therefore, the corrected model demonstrated high versatility in predicting the stress-strain curves for different grades of concrete.
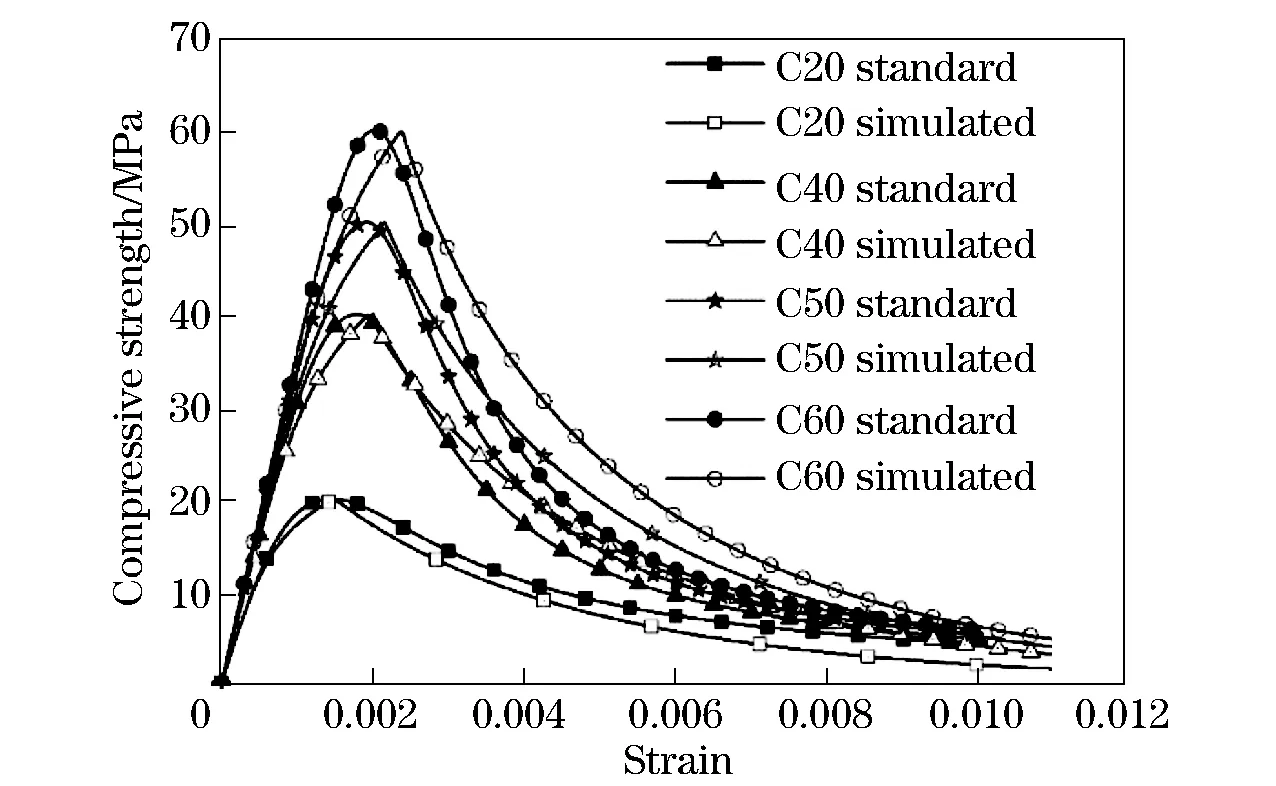
Fig.5 Comparison of the strain-compressive strength curvesbetween the standard codemodel and the optimized model with parameter correction for different grade concretes
In order to further validate the practicability of the corrected concrete model, a conventional triaxial compression test of 5 MPa concrete cylinder was designed with the diameter of 50 mm and the height of 100 mm[10-11]. The testing concrete adopted C20 grade concrete made of 42.5 fast hard sulphate cement, stones (maximum 10 mm) and sand (maximum size 0.5 mm) with the mixed proportion of cement∶sand∶gravel∶water=1.00∶1.91∶2.98∶0.46. The test was carried out on the rock servo triaxial pressure test machine. First, a lateral pressure was applied at the same time with the loading rate of 0.05 MPa/s. After reaching the specified lateral pressure value,the axial pressure continued to be loaded with the loading rate of 0.5-1.0 MPa/s until the specimen was completely destroyed. Fig. 6 exhibited the comparison of the trial curve and simulated curve. It could be seen that the simulated result matched well with the trial result, indicating the accuracy of the corrected model.
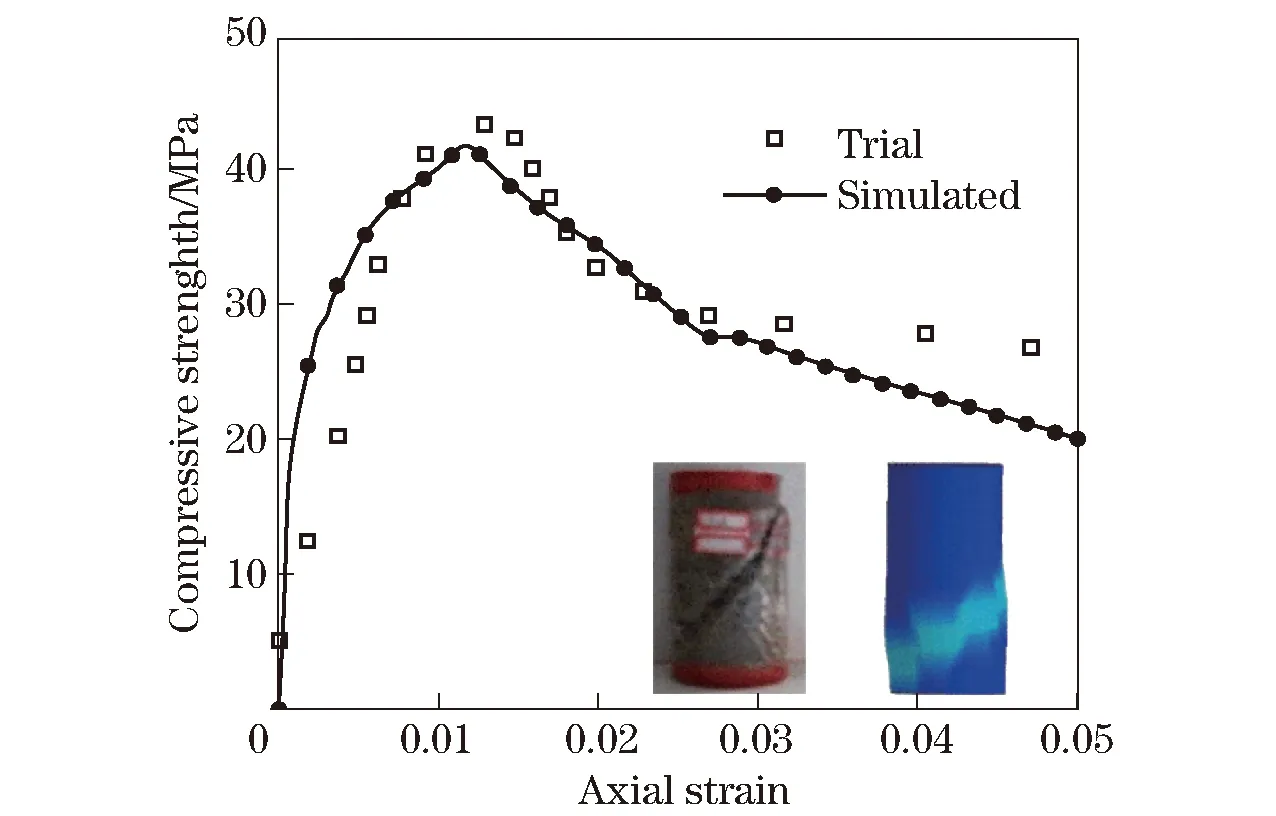
Fig.6 Comparison of axial strain-compressive strength curves between the trial result and simulated result by the optimized model
4 Conclusion
In summary, the sensitivity of hardening ductility parameters (AH, BH, CH, DH) and softening ductility parameter and exponent (AS and BS)in the currently-used concrete damage plastic model was investigated in three load conditions (uniaxial tension, uniaxial compression, triaxial compression) through the convenient cube unit test. The results indicated that the peak strength strain was affected by AH, BH, and CH, but independent of DH.The softening modulus was related with AS in uniaxial compression and triaxial compression, but not affected by AS in uniaxial tension and BS in all three load conditions. Considering the large deviation of the current model using default parameters in LS-DYNA from the standard code model in softening phase, an optimized model with AS correction was proposed. The corrected model with AS=2 (default AS=15) matched well with the code model, and exhibited good feasibility in predicting the stress-strain curve of different grades of concrete. Moreover, the practicability of the corrected model was further validated by the conventional triaxial test. The simulated curve exhibited favorable consistence with the trial curve. Therefore, the model with parameter correction could provide a prospective reference for predicting the mechanical properties of concrete.
[1] Livermore Software Technology Corporation. LS-DYNA keyword user’s manual-Volume Ⅱ material models[M].LS-DYNA R7.1. Livermore, USA: Livermore Software Technology Corporation, 2016.
[2] Sun Xiaowang, Li Yongchi, Huang Ruiyuan, et al. Viscoplastic damage-softening constitutive model for concrete subjected to uniaxial dynamic compression[J]. Journal of Beijing Institute of Technology, 2017, 26(4): 427-433.
[3] Grassl Peter, Jirasek Milan. Damage-plastic model for concrete failure [J]. Science Direct, 2006, 43: 7166-7196.
[4] Menetrey P, Willam K J. A triaxial failure criterion for concrete and its generation [J]. ACI Struct J, 1995, 92: 311-318.
[5] Ortiz M. Constitutive theory for the inelastic behavior of concrete [J]. Mechanics of Materials, 1985, 4: 67-93.
[6] Grassl Peter, Xenos Dimitrios, Nystrom Ulrika, et al. CDPM2: a damage-plasticity approach to modelling the failure [J]. International Journal of Solids and Structures, 2013, 50: 3805-3816.
[7] Kang H, Willam K. Localization characteristics of triaxial concrete model [J]. Journal of Engineering Mechanics, 1999, 125(8):941-950.
[8] Xenos Dimitrios, Grassl Peter. Modelling the failure of reinforced concrete with nonlocal and crack band approaches using the damage-plasticity model CDPM2 [J]. Finite Elements in Analysis and Design, 2016, 57:1-10.
[9] National Standard of the People’s Republic of China. GB 50010—2010 Code for design of concrete structures[S]. Beijing: China Building Industry Press, 2010. (in Chinese)
[10] Jiang Hua, Zhao Jidong. Calibration of the continuous surface cap model for concrete [J]. Finite Elements in Analysis and Design, 2015, 97:1-19.
[11] Li J, Zhang Y X. Evolution and calibration of a numerical model for modelling of hybrid-fibre ecc panels under high-velocity impact [J]. Composite Structures, 2011, 93:2714-2722.
 Journal of Beijing Institute of Technology2018年1期
Journal of Beijing Institute of Technology2018年1期
- Journal of Beijing Institute of Technology的其它文章
- Recommending Personalized POIs from Location Based Social Network
- Dielectric Properties and Microwave Heating of Molybdenite Concentrate at 2.45 GHz Frequency
- Layer-Constrained Triangulated Irregular Network Algorithm Based on Ground Penetrating Radar Data and Its Application
- Online Observability-Constrained Motion Suggestion via Efficient Motion Primitive-Based Observability Analysis
- Particle Filter Object Tracking Algorithm Based on Sparse Representation and Nonlinear Resampling
- Mechanical Performances and Morphology of LDPE/UHMWPE Single-Polymer Composites Produced by Extrusion-Calendering Method
