基于吸收Markov链的网络入侵路径预测方法
胡 浩 刘玉岭 张红旗 杨英杰 叶润国
1(解放军信息工程大学 郑州 450001) 2(中国科学院软件研究所可信计算与信息保障实验室 北京 100190) 3(河南省信息安全重点实验室 郑州 450001) 4 (中国电子技术标准化研究院 北京 100007) (wjjhh_908@163.com)
网络入侵是指攻击者利用目标网络中的一些漏洞,通过实施蓄意的多步骤攻击行为来达到最终的攻击目的,使得网络安全领域面临严峻的考验与挑战[1-3].如臭名昭著的Zeus僵尸网络[2]实施扫描探测、溢出攻击、感染目标主机、病毒传播和窃取用户信息这5个步骤使国家、企业和个人遭受了无法挽回的经济损失.日益泛滥的蠕虫攻击[3]也属多步攻击范畴,防护基于多步攻击的网络入侵刻不容缓.入侵路径预测旨在通过分析网络节点的脆弱性关系,从攻击者角度出发,分析可能的攻击路径,预测潜在的攻击行为,挖掘关键威胁节点,为网络安全主动防御提供重要依据,受到国内外学者的广泛关注[4-20].
早期研究主要围绕设计随机模型来描述多步攻击状态变迁过程,进而利用概率论及数学推理的相关知识来预测可能的状态转移情形.Yu等人[4]利用隐彩色Petri网区分不同攻击行为节点,对告警进行关联,能够预测潜在的攻击路径.吕慧颖等人[5]构造了威胁状态转移图来分析威胁事件的时空关联,实时识别威胁状态,并预测攻击路径.考虑到不同攻击步骤间存在因果关联,王硕等人[6]将单步攻击间的转移概率表示为因果知识,设计了因果知识网络描述网络入侵过程,并利用Dijkstra算法预测不同能力的攻击者在入侵路径选择上的差异性.刘玉岭等人[7]融合攻击方、防护方和网络环境信息,通过时空维度分析,预测了基于攻击威胁的网络安全态势的变化趋势,辅助攻击意图识别和路径预测的研究.
近年来,攻击图(attack graph, AG)[8-22]作为一种基于图论的脆弱性评估模型,已成为研究多步攻击的主流方法,它从攻击者的角度出发,在综合分析多种网络配置和脆弱性信息的基础上,枚举所有可能的攻击路径,从而帮助防御者直观地理解目标网络内各个脆弱性之间的关系,以及由此产生的潜在威胁.目前研究者已开发多种攻击图自动生成工具(如MulVAL,TVA,NetSPA等[8]),兴起了攻击图研究的新一轮热潮.
Kerem[8]综述了攻击图的研究现状,指出攻击图的可达性分析和路径研究是攻击图研究的重点之一.Sheyner等人[9]最早将概率论与攻击图相结合,基于Markov决策过程,利用条件转移概率分析非确定性节点,指出攻击者倾向于选择最有利于实现攻击目标的路径完成状态转移.Sarraute等人[10]改进了Floyd-Warshall算法来预测最短攻击路径.Abraham等人[11]通过分析漏洞生命周期,预测了路径长度随时间的变化规律.针对攻击发生的不确定性问题,刘强等人[12]引入不确定攻击图,利用最佳漏洞利用链,衡量最有可能的攻击路径.陈小军等人[13]在攻击图模型中引入转移概率表,利用观测事件推理单步攻击的不确定性,通过累积概率预测最有可能的攻击路径.Zhu等人[14]利用聚类告警关联分析,借鉴神经网络技术构建完整攻击场景,挖掘潜在的攻击策略.相关研究还包括路径数量评估[15]、路径长度的中位值分析[16]、平均路径长度度量[17]、最短耗时路径预测[18].在实际应用方面,Dai等人[19]分析了如何利用攻击图中的最大风险流路径来预测潜在威胁.通过阻断最大可能攻击路径,Nayot等人[20]设计了网络安全风险的动态评估方法.
梳理以上研究成果发现,尽管现有研究很多,但主要围绕理想攻击场景下的路径预测展开研究,默认每次漏洞利用都能成功实施,包括了最大可能攻击路径、成功概率和路径数量等,然而理想的最大可能攻击路径不一定是攻击者采用的攻击路径,需对攻击路径的概率分布、原子攻击次数和节点威胁度等进行全面感知分析,更全面地辅助安全管理员决策.
针对此问题,本文将吸收Markov链 (absorbing Markov chain, AMC)引入到攻击图研究领域,由于AMC中状态转移具有无后效性和吸收性质,符合网络攻击的随机性和目标状态节点的可达性特点,提出基于吸收Markov链的攻击路径预测方法.首先证明完整攻击图可以映射到吸收Markov链,然后基于通用漏洞评分标准(common vulnerability scoring system, CVSS)[21]提出状态转移概率度量方法,分析并构造状态转移概率矩阵,在此基础上设计2种预测算法,计算节点访问次数期望值和攻击路径长度期望值,最后通过实验验证本文方法的有效性.
本文的主要贡献:1)预测不同攻击状态节点访问次数的期望值,并对节点的威胁进行排序;2)分析不同长度攻击路径的概率分布,并计算路径长度的期望值.前者可用于指导网络安全管理员实施脆弱性修复的优先顺序;后者利于掌握攻击者利用不同路径入侵的可能性,并预测完成攻击目标所需攻击步骤的数量.
1 基于吸收Markov链的攻击图
吸收Markov链适用于随机模型的状态转移预测问题,基本思想是将攻击图映射到吸收Markov链,建立基于吸收Markov链的攻击图模型.一方面Markov链的无后效性符合攻击状态转移仅与相邻状态有关的特点;另一方面,网络攻击至少存在一种终止状态,与吸收Markov链的吸收态相符.
1.1 预备知识
为方便描述,文中主要符号及表达式的含义如表1所示:

Table 1 Symbols and Their Descriptions in This Paper表1 本文主要符号及其描述
定义1. 原子攻击a.指攻击者在网络中实施的单个攻击动作,其可能是对主机服务的扫描或对主机漏洞的1次利用,每个原子攻击动作触发攻击者转移到1个攻击状态S,原子攻击发生的概率为p(a).
定义2. 攻击路径AR.指攻击者从初始状态节点到目标状态节点有向边的集合,攻击路径AR=S1→S2→…→Sn.
定义3. 攻击路径长度RL.指攻击路径中包含的边的数量,即RL=n-1.
定义4. 攻击成功概率p(AR).指攻击路径中所有状态转移都成功的概率p(AR)=p(a1)×p(a2)×…×p(aRL).
定义5. 攻击路径期望长度EARL.指攻击者为实现攻击目标所实施的攻击步骤的数学期望值.
定义6. 状态访问期望次数.指实现攻击目标过程中,某个状态节点访问次数的数学期望值.
定义7. 状态节点威胁排序.指不同状态节点对实现攻击目标的贡献排序,节点排序越靠前,表明该节点的威胁越大.
关于上述定义的3点补充说明:
2) 在定义6中,理想情况下每次状态转移都能成功(对应原子攻击成功实施),而实际情况下,由于攻击者对网络结构不熟悉,原子攻击存在概率,若攻击状态转移失败,看作是对原状态的重复访问,在存在状态重复转移的情况下,求解EARL存在困难性.
3) 在定义7中,对于攻击者而言,漏洞利用越频繁的节点对于实现攻击的贡献值越高,因而对网络安全的威胁越大.本文利用定义6中不同状态节点访问次数期望值的高低对节点威胁进行排序.
1.2 攻击图的概念
攻击图是对多步攻击行为关联建模的有效方法,从攻击者角度出发,描述了攻击状态转移过程,是一个有向图,如图1所示:

Fig. 1 Model of attack graph图1 攻击图模型
定义8. 攻击图AG.使用一个四元组AG=(S,A,E,Δ)来表示,其中,S表示状态节点集合,A表示原子攻击节点集合,E表示为状态节点间的有向边集合,Δ表示状态转移概率集合.
1)S={Si|i=1,2,…,n}表示n个不同状态节点构成的集合;
2)E⊆S×S,∀ei,j∈E,ei,j表示连接节点Si和Sj的边,其中Si表示ei,j的起始状态节点,Sj表示ei,j的目的状态节点,实现状态转移ei,j依赖的原子攻击为a;
3) ∀Δ(ei,j)∈Δ,Δ(ei,j)表示攻击者由状态Si转到状态Sj的概率p(Sj|Si),且Δ(ei,j)等于原子攻击a的发生概率p(a).
利用脆弱性扫描工具如Nessus,Retina[22]对网络进行漏洞扫描,依据部署网络的拓扑结构与采集到的脆弱性集,结合攻击图自动生成工具MulVAL[23]构建攻击图,避免了手动构建的复杂性,是目前的主流构造方法.
1.3 吸收Markov链的相关定义
定义9. Markov链MC[24].对于一个离散的包含有限状态的随机序列集合X={x1,x2,…,xn},如果每个状态值仅与前一个相邻的状态值有关,而与再之前的状态无关,称为Markov链.
p(xi|xi-1,xi-2,…,x1)=p(xi|xi-1).
定义10. 状态转移概率矩阵P.将Markov链中的状态转移概率用邻接矩阵P表示,其中pi,j表示状态xi→xj的概率,若xi→xj不可达,令pi,j=0,矩阵P满足

其中,0≤pi,j≤1(1≤i,j≤n).
定义11. 初始状态.表示攻击者的出发状态,该状态节点只有流出边,没有流入边.
定义12. 吸收状态.表示攻击者的目标状态,该状态节点只有流入边,没有流出边.
定义13. 过渡状态.状态序列中,除去吸收状态的其他状态称为过渡状态.
定义14. 吸收Markov链AMC[24].含有吸收状态的Markov链称为吸收Markov链,对应状态转移概率矩阵表示为

其中,Q是t×t的矩阵,表示过渡状态间的转移概率;0是r×t的零矩阵;R是t×r的非零矩阵,表示过渡状态到吸收状态的转移概率;I是r×r的单位矩阵;所有状态数量n=t+r.
1.4 攻击图到吸收Markov链的映射
本节给出攻击图中状态转移概率的归一化处理算法,并生成状态转移概率矩阵,在此基础上证明完整的攻击图可以映射到吸收Markov链.
命题1. 1个完整的攻击图中至少包含1个吸收状态.
证明. 由于攻击图描述了网络的脆弱性利用关系,通过基于脆弱性利用的多步关联,攻击者最终将达到稳定的终止状态,因此攻击图的终止状态即吸收状态,且至少包含1个吸收状态.
证毕.
攻击图边值归一化处理的具体算法步骤如下:
算法1. 状态转移概率归一化算法.
输入:攻击图AG=(S,A,E,Δ);
输出:吸收Markov链AMC的状态转移概率矩阵P.
步骤1. 令i,j=1,G=S,其中i和j分别表示矩阵P的第i行和第j列;
步骤2. 令k=1,k表示节点Si的第k条流出边的编号;
步骤4. 对于节点Si∈S,从节点集合G中随机选取1个节点Sj,令G={G-Sj};
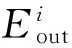
步骤6. 令j=j+1,若j≤n,则转至步骤4,否则该步骤结束,令j=1,k=1,G=S;

按序赋值给矩阵P中第i行位置(i,j1),(i,j2),…,(i,jk)上的元素值pi,j1,pi,j2,…,pi,jk,该步骤结束;
步骤8. 令i=i+1,若i≤n,则转至步骤1,对于每个状态节点Si,重复步骤4~6,完成节点Si流出边的概率值归一化处理,并生成矩阵P的第i行;若i>n,则该步骤结束;
步骤9. 输出状态转移概率矩阵P,算法结束.

命题2. 1个完整的攻击图可以映射为1个吸收Markov链,若以下2个条件成立:
1) 对于任意状态节点Si满足定义10,即该节点的所有流出边的概率之和等于1;
2) 至少包含1个吸收状态节点.
证明. 1)利用算法1,得到任意节点Si满足:
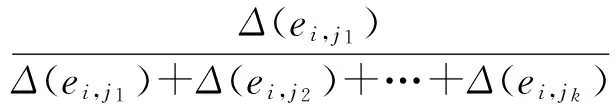
2) 由命题1可知条件2)满足.
综上,命题2成立.
证毕.
图1攻击图对应的Markov链的状态转移概率矩阵如下:

Fig. 2 Exploitability scoring standard of CVSS图2 CVSS的漏洞可利用性评分标准
2 攻击路径预测
在第1节的基础上,本节首先给出一种通用的基于CVSS的转移概率度量方法,然后分析节点访问次数的期望值,最后计算攻击路径长度的期望值.
2.1 基于CVSS的转移概率度量
CVSS由美国国家基础建设咨询委员会发布,是漏洞评估的行业公开标准,其制定的漏洞可利用性评分准则(如图2所示)全面衡量了漏洞的利用难度,通过查询美国国家漏洞数据库(national vulner-ability database, NVD)[25]可以得到具体值.本文利用攻击难度来度量状态转移概率,给出一种基于CVSS的转移概率度量方法,以增强研究的通用性.
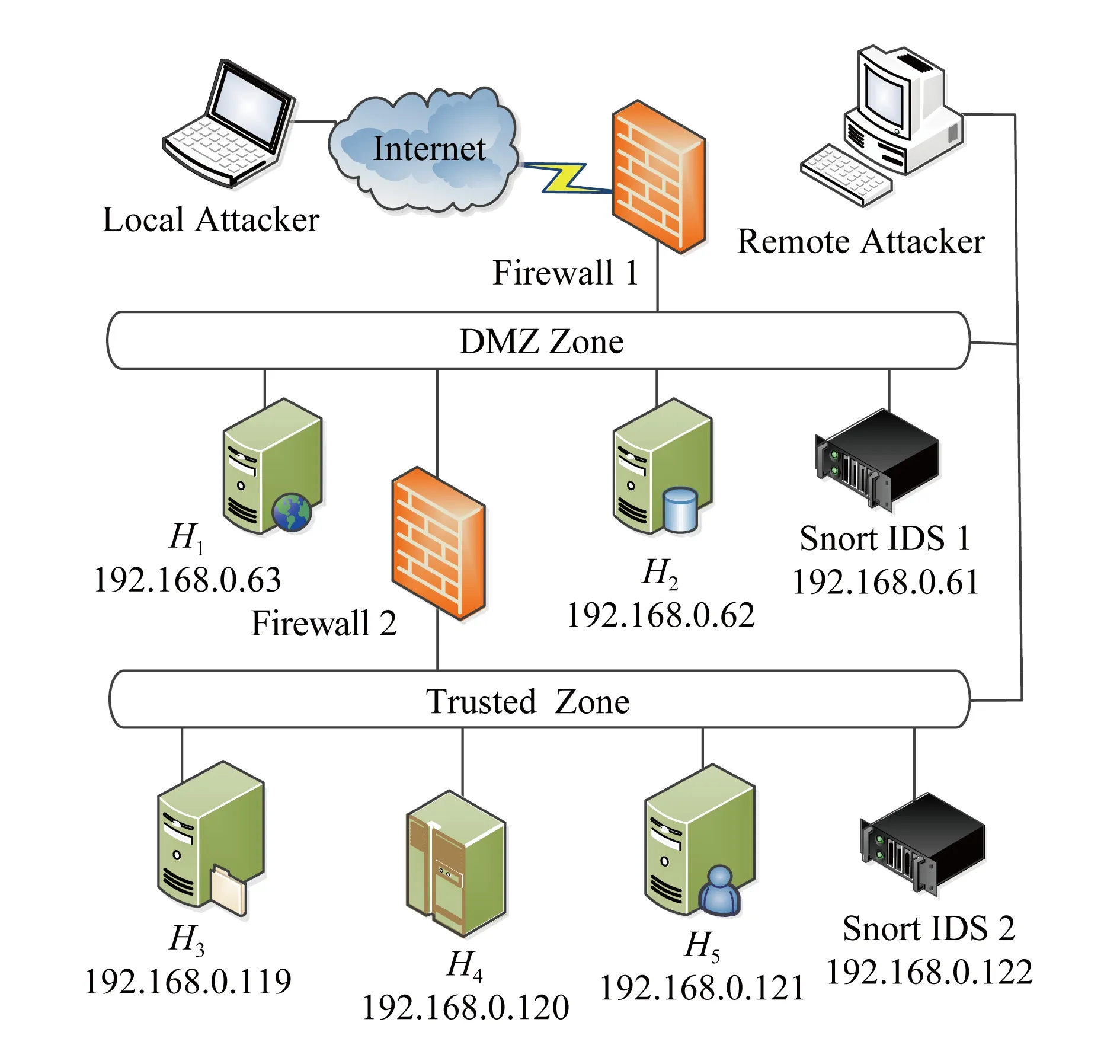
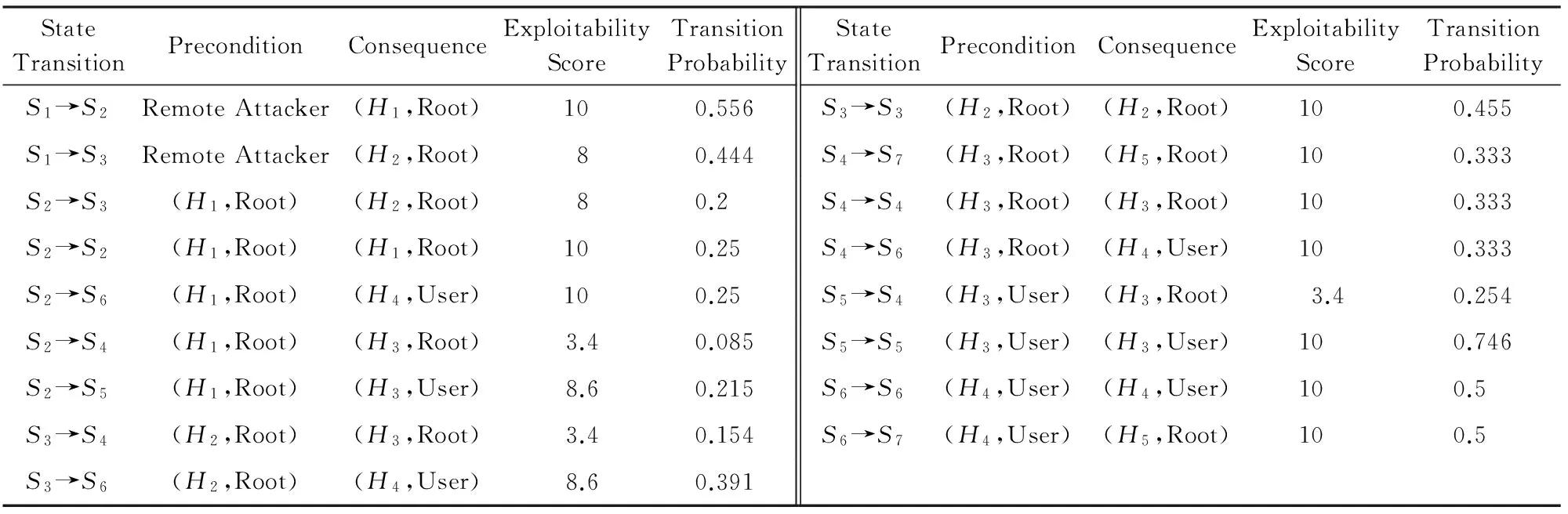
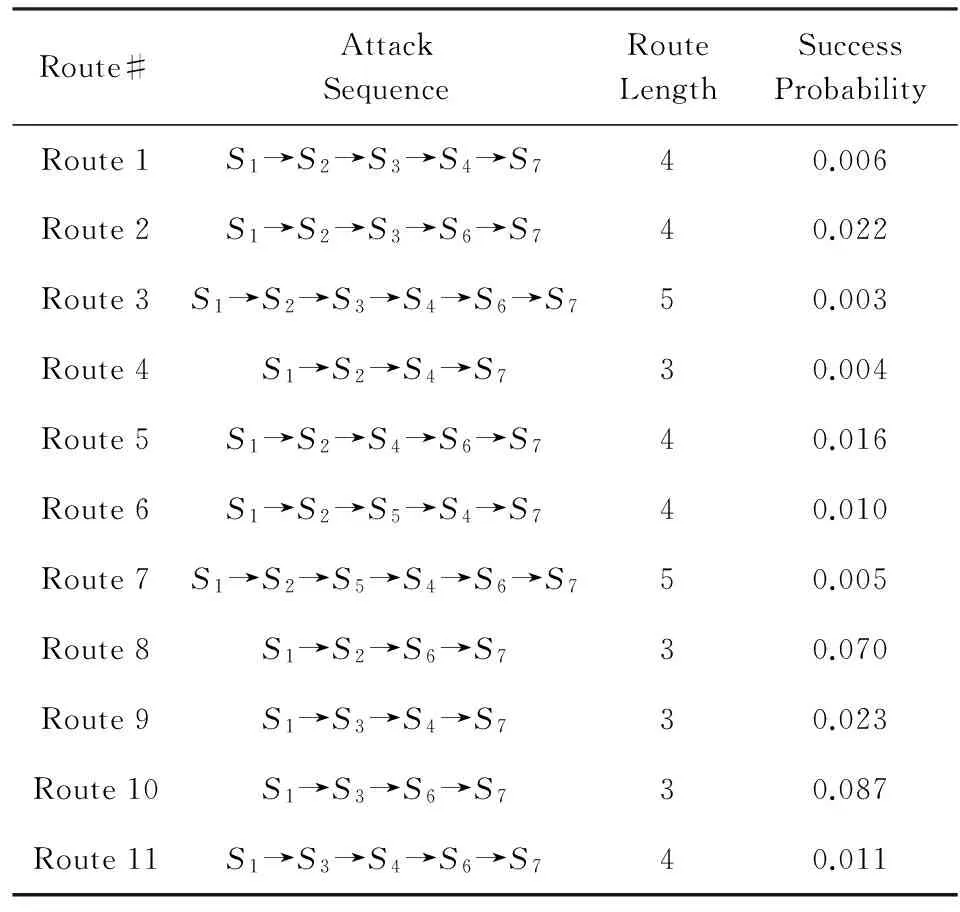
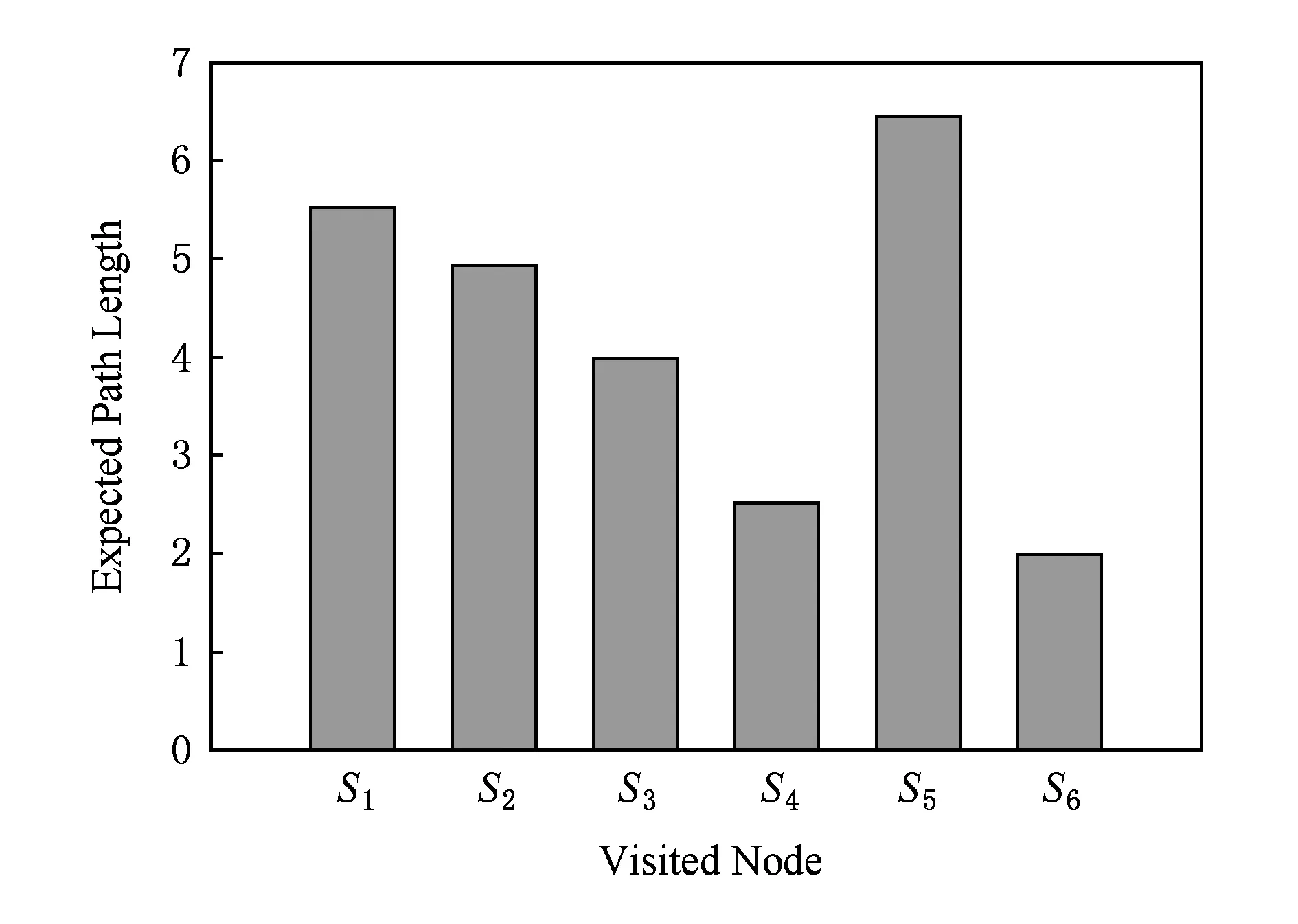
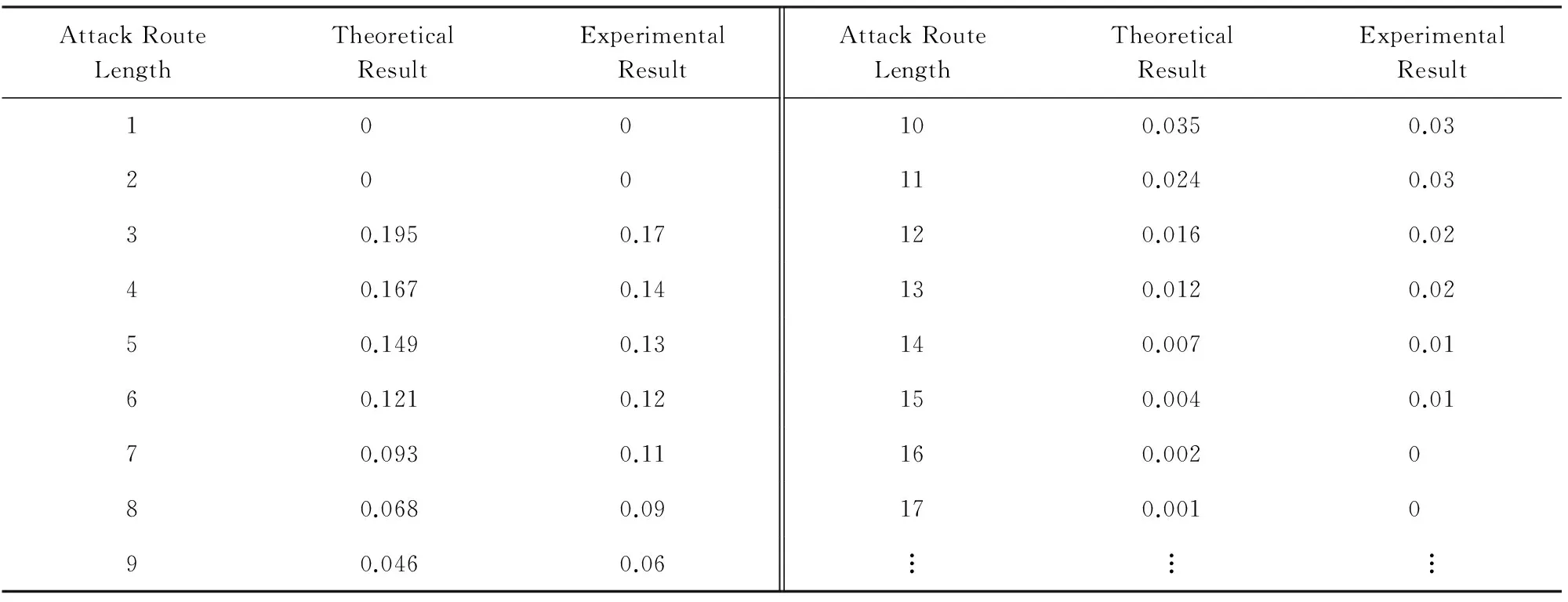
由图2可知,CVSS给出原子攻击a依赖漏洞的可利用性得分score(a)=20×AV×AC×AU,且0 设攻击图AG中状态转移边e的概率值与依赖原子攻击a的可利用性得分score(a)成正比,即Δ(e)=f×score(a),其中f是比例系数.对于任意节点Si的流出边ei,j1,ei,j2,…,ei,jk,利用算法1标准化处理后的转移概率为 本节首先给出吸收Markov链中状态转移满足的若干引理,其中引理1给出n步攻击后的AMC的状态转移概率矩阵,引理2证明经过n(n→∞)步后,过渡状态间的转移概率为0,在此基础上结合概率论,定理1得到状态节点访问次数的期望值求解矩阵,最后给出节点访问次数期望值计算流程. 证明. 利用数学归纳法进行证明: 1) 当m=2时,由下式可知结论成立 2) 假设当m=m-1时结论成立,即: 则满足: 因此假设成立,由1)2)可知引理1成立. 证毕. 引理2. 攻击者从任意非吸收状态出发,最终都会到达吸收状态,即经过m(m→∞)步后,过渡状态间的期望转移概率为0,满足: 证毕. 定理1. 攻击者从过渡状态Si出发,在吸收前访问过渡状态Sj的次数期望值用Ni,j表示,其中1≤i,j≤t,设N为大小为t×t的矩阵,将Ni,j赋值给矩阵N中位置(i,j)元素,称N为攻击次数期望值矩阵,则N=(I-Q)-1. 证明. 1) 攻击者从节点Si出发,分别经过m=0,1,2,3,…步,访问节点Sj的次数期望值总和 综合1)2)可知,定理1成立. 证毕. 基于网络拓扑结构和漏洞扫描信息,利用自动生成工具MulVAL生成攻击图AG,通过查询NVD数据库得到漏洞可利用性得分,在此基础上给出节点访问次数的期望值预测步骤如下: 方法1. 节点访问次数的期望值预测方法. 输入:攻击图AG、所有漏洞的可利用性得分score(a); 输出:以状态节点Si为初始节点,在吸收前转移到节点S1,S2,…,St的期望次数Ni,1,Ni,2,…,Ni,t,以及节点威胁排序. 步骤1. 依据算法1,利用2.1节转移概率度量方法,结合AG的漏洞可利用性得分生成AMC的n×n的状态转移概率矩阵P,其中矩阵P的第i行向量的位置(i,j1),(i,j2),…,(i,jk)上的元素值为 其余位置的元素值为0; 步骤2. 由矩阵P构造t×t的过渡状态间的转移概率矩阵Q; 步骤3. 计算t×t期望值矩阵N=(I-Q)-1,输出行向量(Ni,1,Ni,2,…,Ni,t); 步骤4. 依据(Ni,1,Ni,2,…,Ni,t)中元素值大小对节点S1,S2,…,St的威胁进行排序,步骤结束. 下面以图3攻击图为例,简要说明方法流程. The value next to the arrow line means the transition probability from one state to another.Fig. 3 Example of attack graph图3 攻击图实例 为简化说明,图3中状态转移概率值已归一化处理,过渡状态为S1,S2,S3,吸收状态为S4,得到状态转移概率矩阵Q和P,并计算期望值矩阵N. 由N的第1行可知,从初始状态S1出发,访问节点S2,S3次数的期望值为87,57,此时节点的威胁排序为S2>S3. 本节在2.2节的基础上,首先给出求解攻击路径长度的期望值向量的推论,在此基础上分析路径长度的期望值计算过程. 推论1. 攻击者从节点Si(1≤i≤t)出发,吸收前转移总次数的期望值(期望路径长度)用Ti表示,设T是大小为t×1的矩阵,C是大小为t×1的单位矩阵,将Ti赋值给T位置(i,1)的元素,称T为期望路径长度矩阵,则T=N·C. 证明. 由定理1可知,对于任意节点Si,在吸收前转移到节点S1,S2,…,St的次数分别为Ni,1,Ni,2,…,Ni,t,则从节点Si出发的期望攻击路径长度Ti=Ni,1+Ni,2+…+Ni,t,因此T=(Ti)=(Ni,1+Ni,2+…+Ni,t)=N·C. 结合拓扑分析和漏洞扫描,利用工具MulVAL生成攻击图,查询NVD数据库得到漏洞信息,并设计攻击路径长度的期望值预测方法如下: 方法2. 攻击路径长度的期望值预测方法. 输入:攻击图AG、所有漏洞的可利用性得分score(a); 输出:状态节点Si作为初始节点,攻击路径长度的期望值Ti. 步骤1. 结合算法1和方法1,构造AMC的n×n状态转移概率矩阵P,位置(i,j1),(i,j2),…,(i,jk)值为 第i行其余元素值为0; 步骤2. 构造AMC的过渡状态间的转移概率矩阵Q,大小为t×t; 步骤3. 计算t×t的访问次数期望值矩阵N=(I-Q)-1; 步骤4. 令C=(1,1,…,1)T,大小为t×1,计算t×1的路径长度期望值向量T=N·C,输出节点Si出发的路径长度的期望值EARL(Si)=Ti,步骤结束. 计算复杂度分析如下: 1) 算法执行包含矩阵求逆、矩阵相加和矩阵相乘过程,其中矩阵相乘的时间复杂度最高,当2个n×n矩阵相乘时,包含2n3次乘法运算,因此时间复杂度的阶数为O(n3). 2) 算法需要维护n×n矩阵P、t×t矩阵Q、t×t矩阵N、t×1矩阵T和C,因此存储复杂度为O(n2). 综上,算法复杂度符合多项式时间级别,在当前计算环境下能够执行实时运算. 对于图3的攻击图, 则从节点S1,S2,S3出发的攻击路径长度的期望值为207,127,157. 结合引理2及定理1, 结合定义14,[Ν·R]i,j表示攻击者由过渡状态Si转移到吸收状态Sj的概率.计算 验证任何过渡状态最终都会以概率1转移到吸收状态. 为了验证本文方法的有效性和适用性,我们设计了2个实验对该方法进行了测试分析.其中实验1参照文献[6]搭建了一个小型模拟攻防环境;实验2选用林肯实验室提供的经典DARPA2000标准测试集[26],分析DDOS攻击场景下的实验结果.最后给出本方法与现有方法的综合对比分析. Fig. 4 Experimental network topology图4 实验网络拓扑结构 为验证本文方法的有效性,搭建了一个实际网络来进行测试.实验拓扑如图4所示,网络中包括防火墙、入侵检测系统Snort IDS、2台主机以及3台服务器.防火墙预先设置策略将网络分为2个子网,使得服务器H1,H2分布在DMZ Zone,服务器H3,H4,H5分布在Trusted Zone.防火墙1禁止外部主机访问Trusted Zone中的服务器,仅可以利用HTTP协议(80端口)与DMZ Zone内的主机H1和H2进行通信.防火墙2允许DMZ Zone内的主机和Trusted Zone中的服务器进行通信,且Trusted Zone内的服务器仅可以被动接收服务请求.依据攻击发起的初始位置,攻击分为内部和外部攻击2种. 3.1.1 实验环境信息 利用脆弱性扫描工具Nessus对各网段进行扫描,并通过查询NVD得到各主机包含的漏洞信息如表2所示: Table 2 Host Configuration and Vulnerability Information in Network表2 网络主机配置及漏洞信息 依据部署网络的拓扑结构与采集的脆弱性集,利用工具MulVAL生成攻击图如图5所示,不同状态间转移依赖的漏洞已标注,到节点自身的状态转移边用虚线标出,边值标注为状态转移的可利用性得分,共有7种不同的攻击状态,S1表示外部攻击者的初始状态,各状态信息描述如表3所示: The value next to the arrow line means the exploitability score of vulnerability. Fig. 5 Attack graph of experimental network图5 实验网络攻击图 No.DescriptionNo.DescriptionS1RemoteAttackerS5(H3,Root)S2(H1,Root)S6(H4,User)S3(H2,Root)S7(H5,Root)S4(H3,User) 3.1.2 计算过程描述 步骤1. 基于CVSS的转移概率度量. 利用2.1节状态转移概率归一化方法,生成吸收Markov链的状态转移概率表,如表4所示,对应吸收Markov链攻击图如图6所示. Table 4 Probability Table of State Transition表4 状态转移概率表 Fig. 6 Absorbing Markov chain attack graph图6 吸收Markov链攻击图 步骤2. 节点访问次数的期望值预测. 理想情况下,若入侵场景中的每次漏洞利用都成功实施,所有可能的11条入侵路径及其概率分布如表5所示,其中最短路径长度为3,最长路径长度为5,路径长度的中位值为4,理想路径长度的平均值为(4+4+5+3+4+4+5+3+3+3+4)11=3.818.最大可能攻击路径为S1→S3→S6→S7,累积成功概率为0.444×0.391×0.5=0.087,该攻击过程描述如下:为获得服务器H5的root权限,攻击者首先对目标网络进行IPsweep地址扫描,搜寻有效主机,发现有效主机H2,通过端口扫描,发现其通信端口为80,利用postgresql服务上的漏洞CVE 2014-0063,获得root权限;随后攻击者利用bmc服务上的漏洞CVE 2013-4782获得服务器H4的用户权限;进一步以服务器H4为跳板,利用radius服务上的漏洞CVE 2014-1878获得服务器H5的root权限,实现攻击目标. Table5LengthandProbabilityDistributionofIdealAttackRoute 表5 理想攻击路径长度及其概率分布 在实际情况下,若单步攻击的某次漏洞利用不成功,则状态转移失败,看作到自身状态的1次转移,路径长度加1,因而实际的攻击路径长度往往高于理论的攻击路径长度,下面利用本文方法分析实际网络环境中的路径预测信息. 由图6得到状态转移概率矩阵P和Q,结合方法1和方法2计算期望矩阵N和T如下所示: 期望值矩阵N的不同行代表从不同初始状态出发访问各节点次数的期望值分布,如图7所示.若节点访问次数越高,表明该节点的威胁程度越大,不同节点的访问次数分布不均匀,表明各节点的威胁程度差别较大.例如外部攻击者从状态S1出发,访问节点S2,S3,S4,S5,S6的次数分别为0.741,1.087,0.584,0.628,1.610,此时节点威胁排序为S6>S3>S2>S5>S4,因此在漏洞修复时应首先考虑状态S6(H4上的漏洞CVE 2013-4782). Fig. 7 Distribution of expected number of visits to different state nodes图7 不同状态节点访问次数的期望值分布 步骤3. 攻击路径长度的期望值预测. 结合图6,由矩阵T可知,从不同节点S1,S2,S3,S4,S5,S6出发,到达攻击目标S7的期望路径长度分布如图8所示,例如初始状态为S1时的期望攻击路径长度为5.65,表示攻击者平均需要实施5.65次原子攻击才能实现攻击目标.通过实时检测攻击发生的位置,确定攻击者的状态,可以预测后续攻击的期望路径长度,对于安全管理员实时掌握当前的攻击状况、制定安全防护措施具有重要意义. Fig. 8 Expected attack route length starting from different initial state nodes图8 从不同状态节点出发的期望攻击路径长度 3.1.3 测试结果分析 借鉴文献[6]的实验方法,从课题依托信息安全重点实验室中随机挑选100名学员作为攻击者,分别在部署环境(如图4所示)中进行攻击测试实验,攻击者的初始状态为S1,公开网络的拓扑结构及漏洞信息,既定攻击目标为S7,实验时间为2 h.通过实时采集网络中运行的防火墙、Snort IDS和主机日志的告警信息,进一步利用自动化工具ArCSight[27]分析告警信息,得到100条攻击序列,由于4名攻击者未在规定时间内完成攻击目标,剔除未成功的4条攻击序列后,统计长度为3~17的路径数量分别为17,14,13,12,11,9,6,3,3,2,2,1,1,0,0. Table 6 Probability Distribution of Attack Route Length by Our Method表6 本文攻击路径长度的概率分布 从图9可以看出: 1) 长度为3的路径出现概率最大,与本文理论预测结果一致,同时概率值随着路径长度的增大而不断减小,理论值表明当路径长度不断增大时出现概率逐渐趋于0,验证了本文方法的有效性. 2) 实验包含100名攻击者,采集到100个样本,受攻击者自身因素(知识水平、攻击技能、攻击经验等)的影响,不同路径长度出现概率的测试值与理论值不完全相等,但从整体上看,路径长度概率分布的测试结果与理论结果的变化趋势基本一致,符合预期结果. Fig. 10 Attack graph of LLDOS1.0 scenario图10 LLDOS1.0场景的攻击图 本节以林肯实验室提供的DARPA2000数据集中LLDOS1.0攻击场景作为实验对象,文献[14]通过基于聚类的告警关联分析,挖掘了该数据集包含的完整攻击场景,如图10所示,受到广泛认可,并给出如下状态转移概率,本文借鉴该攻击场景进行实验分析: Δ(e2,5)=0.15, 利用算法1构造吸收Markov链的转移矩阵P,进一步利用算法2和算法3计算矩阵N和T: 吸收状态节点为S5,Ni,j表示状态Si出发,在到达目标状态之前访问状态Sj的次数,例如从初始状态节点S1出发,到达节点S2,S3,S4的次数分别为0.84,5.38,0.98,此时过渡状态节点威胁排序为S3>S4>S2,应首先修复状态S3的漏洞.由矩阵T可知,从不同节点S1,S2,S3,S4出发,到达目标节点的期望攻击路径长度分别为8.198,7.2,7.692,7.197,结果表明从节点S1出发的攻击者,到达目标状态节点所实施漏洞攻击的平均次数最多. 表7给出了LLDOS1.0攻击场景中理想度量方法和实际度量方法的结果比较,在理想情况下,由于不存在重复状态转移行为,统计得到可能路径数量为8,最短路径长度为2,路径长度类型有2,3,4,所有路径长度的中位值及平均值都是3,攻击意图的累积成功概率为0.14. 相反,在实际情况下,实现攻击意图的期望概率为1,最长和最短期望路径长度分别为8.198和7.197,前者表明平均需要实施8.198次漏洞攻击才能实现目标,后者表明所需要的最少漏洞攻击次数为7.197,该结果显然大于理想路径长度值,与预期相符.因此,利用本文度量方法可以科学评估攻击者当前状态,并准确预测后续攻击行为. 表7 Structural Metrics of LLDOS1.0 Attack Scenario表7 LLDOS1.0攻击场景的结构化度量 本文与典型相关研究的特点比较如表8所示,从表8中可以看出,多数文献均有研究最大可能攻击路径及其概率值.针对理想攻击场景(每次漏洞利用都成功),本文和文献[6,10,16-17]进一步分析了最短路径,除此之外,本文和文献[6,15-17]能够度量理想攻击路径的数量,其中文献[16-17]和本文又分析了理想路径长度的平均值,且本文和文献[16]进一步讨论了理想路径长度的中位值. Table 8 Comparison of Features Among Our Method and Others表8 本文与典型方法的特点比较 特别地,针对实际网络环境(单步攻击实现依赖多次漏洞利用),本文重点研究了期望路径长度及其概率分布,并给出了状态节点访问次数的期望值预测方法,用于分析节点的威胁排序,更加准确全面地预测攻击路径信息,辅助安全管理员决策,为实际网络环境中应对网络多步攻击威胁提供更多指导. 由于网络入侵者的攻击状态转移过程复杂,因此攻击路径预测对于安全管理员直观地了解攻击过程具有重要意义.考虑到现有方法主要围绕理想攻击路径展开研究,本文将攻击图映射为吸收Markov链,给出了基于通用漏洞评分标准的转移概率量化方法,在此基础上着重研究了实际网络环境中不同状态节点的期望访问次数,用于分析节点的威胁排序,并计算期望攻击路径长度及其概率分布,辅助安全管理员全面分析不同攻击路径的发生概率,掌握攻击者可能实施的原子攻击次数,并预先制定安全防护措施,为防御网络入侵提供指导. 如何结合网络中采集的告警序列,客观地衡量状态转移概率,预测攻击路径长度的期望值,并依据实时观察结果动态修正后续路径长度的期望值,提高复杂攻击场景中预测的准确性和适用性是下一步研究的主要工作. [1]Zhang Huanguo, Han Wenbao, Lai Xuejia, et al. Survey on cyberspace security[J]. Scientia Sinica Informationis, 2016, 46(2): 125-164 (in Chinese)(张焕国, 韩文报, 来学嘉, 等. 网络空间安全综述[J]. 中国科学: 信息科学, 2016, 46(2): 125-164) [2]Jiang Jian, Zhuge Jianwei, Duan Haixin, et al. Research on botnet mechanisms and defenses[J]. Journal of Software, 2012, 23(1): 82-96 (in Chinese)(江健, 诸葛建伟, 段海新, 等. 僵尸网络机理与防御技术[J]. 软件学报, 2012, 23(1): 82-96) [3]Liu Yuling, Feng Dengguo, Wu Lihui, et al. Performance evaluation of worm attack and defense strategies based on static Bayesian game[J]. Journal of Software, 2012, 23(3): 712-723 (in Chinese)(刘玉岭, 冯登国, 吴丽辉, 等. 基于静态贝叶斯博弈的蠕虫攻防策略绩效评估[J]. 软件学报, 2012, 23(3): 712-723) [4]Yu Dong, Frincke D. Improving the quality of alerts and predicting intruder’s next goal with hidden colored Petri-net[J]. Computer Networks, 2007, 51(3):632-654 [5]Lü Huiying, Peng Wu, Wang Ruimei, et al. A real-time network threat recognition and assessment method based on association analysis of time and space[J]. Journal of Computer Research and Development, 2014, 51(5): 1039-1049 (in Chinese)(吕慧颖, 彭武, 王瑞梅, 等. 基于时空关联分析的网络实时威胁识别与评估[J]. 计算机研究与发展, 2014, 51(5): 1039-1049) [6]Wang Shuo, Tang Guangming, Kou Guang, et al. Attack route prediction method based on causal knowledge[J]. Journal on Communications, 2016, 37(10): 188-198 (in Chinese)(王硕, 汤光明, 寇广, 等. 基于因果知识网络的攻击路径预测方法[J]. 通信学报, 2016, 37(10): 188-198) [7]Liu Yuling, Feng Dengguo, Lian Yifeng, et al. Network situation prediction method based on spatial-time dimension analysis[J]. Journal of Computer Research and Development, 2014, 51(8): 1681-1694 (in Chinese)(刘玉岭, 冯登国, 连一峰, 等. 基于时空维度分析的网络安全态势预测方法[J]. 计算机研究与发展, 2014, 51(8): 1681-1694) [8]Kerem K. A taxonomy for attack graph generation and usage in network security[J]. Journal of Information Security and Applications, 2016, 29(C): 27-56 [9]Sheyner O, Haines J, Jha S, et al. Automated generation and analysis of attack graphs[C]Proc of the 2002 IEEE Symp on Security and Privacy. Piscatawary, NJ: IEEE, 2002: 273-284 [10]Sarraute C, Richarte G, Lucángeli O J. An algorithm to find optimal attack routes in nondeterministic scenarios[C]Proc of the 4th Int ACM Workshop on Security and Artificial Intelligence. New York :ACM, 2011: 71-80 [11]Abraham S, Nair S. A predictive framework for cyber security analytics using attack graphs[J]. International Journal of Computer Networks & Communications, 2015, 7(1): 1-17 [12]Liu Qiang, Yin Jianping, Cai Zhiping, et al. Uncertain-graph based method for network vulnerability analysis[J]. Journal of Software, 2011, 22(6): 1398-1412 (in Chinese)(刘强, 殷建平, 蔡志平, 等. 基于不确定图的网络漏洞分析方法[J]. 软件学报, 2011, 22(6): 1398-1412) [13]Chen Xiaojun, Fang Binxing, Tan Qingfeng. Inferring attack intent of malicious insider based on probabilistic attack graph model[J]. Chinese Journal of Computers, 2014, 37(1): 62-72 (in Chinese)(陈小军, 方滨兴, 谭庆丰. 基于概率攻击图的内部攻击意图推断算法研究[J]. 计算机学报, 2014, 37(1): 62-72) [14]Zhu Bin, Ghorbani A A. Alert correlation for extracting attack strategies[J]. International Journal of Network Security, 2006, 3(3): 244-258 [15]Ortalo R, Deswarte Y, Kaaniche M. Experimenting with quantitative evaluation tools for monitoring operational security[J]. IEEE Trans on Software Engineering, 1999, 25(5): 633-50 [16]Idika N, Bhargava B. Extending attack graph-based security metrics and aggregating their application[J]. IEEE Trans on Dependable & Secure Computing, 2012, 9(1):75-85 [17]Li Wei, Vaughn R B. Cluster security research involving the modeling of network exploitations using exploitation graphs[C]Proc of the 6th IEEE Int Symp on CLUSTER Computing and the Grid. Piscatawary, NJ: IEEE, 2006: 26-26 [18]Lucangeli J, Sarraute C, Richarte G. Attack planning in the real world [JOL]. Computer Science, 2013[2017-06-17]. http:sciencewise.infoarticles1306.4044 [19]Dai Fangfang, Hu Ying, Zheng Kangfeng, et al. Exploring risk flow attack graph for security risk assessment[J]. IET Information Security, 2015, 9(6): 344-353 [20]Nayot P, Rinku D, Indrajit R. Dynamic security risk management using Bayesian attack graphs[J]. IEEE Trans on Dependable & Secure Computing, 2012, 9(1): 61-74 [21]Schiffman M. Common vulnerability scoring system (CVSS)[EBOL]. [2017-06-17]. https:www.first.orgcvss [22]Tenable N. Nessus vulnerability scanner[EBOL]. [2017-06-17]. http:www.tenable.comproductsnessus-home [23]Ou Xinming, Govindavajhala S, Appel A W. MulVAL: A logic-based network security analyzer[C]Proc of the 14th USENIX Security Symp. Berkeley, CA: USENIX Association, 2005: 8-8 [24]Dimitri P, Bertsekas J N. Introduction to probability[EBOL]. [2017-06-17]. http:www.sciencedirect.comsciencebook9780128000410 [25]NIST. National vulnerability database[DBOL]. [2017-06-17]. https:nvd.nist.gov [26]MIT Lincoln Laboratory. 2000 DARPA intrusion detection scenario specific data sets[EBOL]. [2017-06-17]. http:www.ll.mit.eduidevaldata2000data.html [27]Hewlett-Packard. ArcSight ESM enterprise security manager[OL]. [2017-06-17]. https:saas.hpe.comen-ussoftwaresiem-security-information-event-management HuHao, born in 1989. PhD candidate. His main research interests include network security assessment and visual cryptography. LiuYuling, born in 1982. PhD. Associate professor. His main research interests include network and system security assessment and network security situation awareness. ZhangHongqi, born in 1962. PhD, professor. His main research interests include network security and classification protection. YangYingjie, born in 1971. PhD, professor. His main research interests include security management and situation awareness. YeRunguo, born in 1976. PhD. Engineer. His main research interest is the big data security.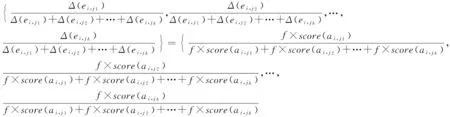
2.2 节点访问次数的期望值预测

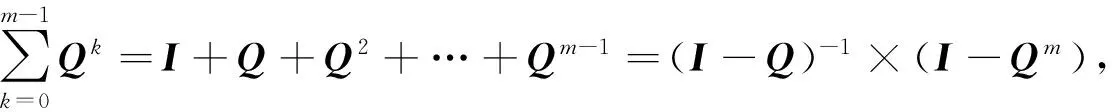
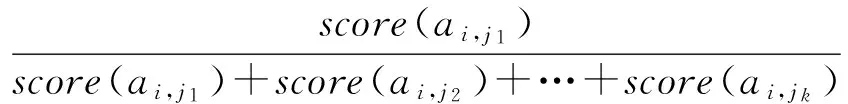

2.3 攻击路径长度的期望值预测
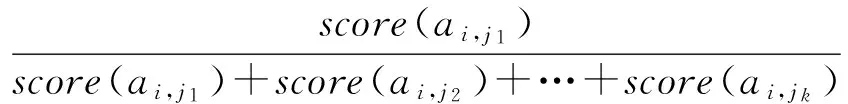
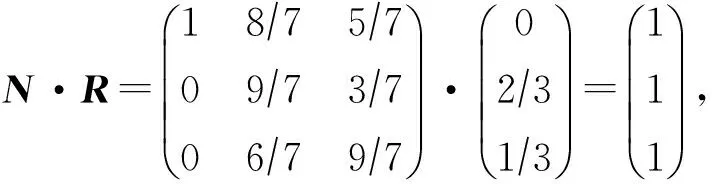
3 实验与分析
3.1 实验1






3.2 实验2

Δ(e2,3)=0.28,
Δ(e3,5)=0.1,
Δ(e1,2)=0.29,
Δ(e2,2)=0.2,
Δ(e2,4)=0.28,
Δ(e4,2)=0.18,
Δ(e4,3)=0.42,
Δ(e4,5)=0.15,
Δ(e5,5)=1,
Δ(e1,4)=0.33,
Δ(e4,4)=0.18.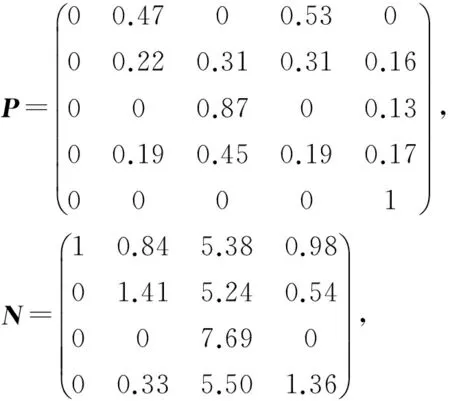

3.3 方案综合对比
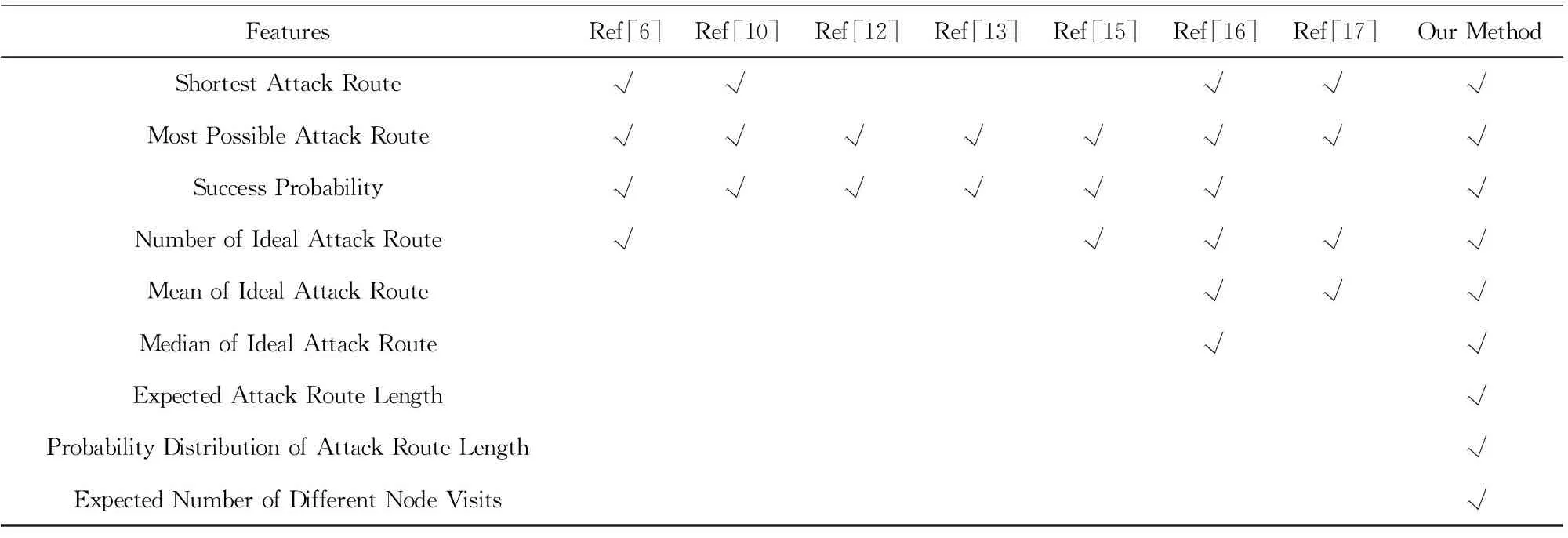
4 结束语






