基于链路状态数据库的数据中心网络异常检测算法
许 刚 王 展 臧大伟 安学军
1(中国科学院计算技术研究所高性能计算机研究中心 北京 100190) 2 (中国科学院大学 北京 100049) (xugang10@ict.ac.cn)

Fig. 1 Traditional data-center topology图1 传统数据中心拓扑结构
随着云计算和大数据的发展,数据中心(Internet data center, IDC)建设迎来高潮.当前数据中心应用如在线零售、搜索、社交网络、云盘、广告推荐系统等通常需要高带宽的稳定网络,然而在网络故障或路由抖动时,这些应用系统经常会在用户访问和业务服务器之间产生路由频繁抖动的情况,路由抖动会导致用户访问和企业收入明显减少.
数据中心网络会频繁发生网络抖动,导致丢包增多、时延增大和吞吐量下降,已成为数据中心的性能瓶颈,严重影响业务的性能和服务质量.当网络发生故障时,故障定位对网工来说是一个非常棘手的问题,现有的解决方案主要包括2种:1)通过搜集网络设备上系统日志使用3-sigma、分段3-sigma、Holt-winters和 ARIMA等机器学习方法进行异常检测[1];2)经验丰富的网工根据自身经验结合故障特征手动解决.然而无论是通过算法还是经验进行故障发现和设备定位普遍都是预测性的,仍然会出现误判和误报的问题,且实时性不高.
针对这一问题,我们提出基于链路状态数据库(link state database, LSDB)的数据中心网络异常检测方法LSAP,通过搜集LSDB,利用改进Dijkstra算法重计算全网路由形成路由择域信息库(routing information base, RIB),根据LSDB快照和RIB快照比对关联链路变化和路由变化进行异常定位,发现网络问题.
1 背景和相关工作
1.1 数据中心的网络
传统数据中心网络是由核心层、汇聚层和接入层3层网络设备组成[2].如图1所示,网络呈现出由底层网络的物理服务器到上层网络的核心路由器所组成的3层网络层次结构,其中核心层设备接入上层网络,核心层设备与汇聚层设备相连,汇聚层设备与接入层设备相连,接入层设备与底层物理服务器相连.核心层位于全局网络的顶端,核心层的路由连接在整个数据中心网络中起到关键的作用,通常会在设备之间建立冗余连接提高网络稳定性.
伴随着业务访问量的增长,数据中心所需的服务器数量也在持续增长,为满足用户访问BAT(Baidu Alibaba Tencent)数据中心平均每月就有2 000台以上的服务器上线.为降低数据中心计算节点间的通信延时,减少网络中间层次、网络扁平化势在必行.如图2所示,网络扁平化后对核心设备交换能力要求降低,网络既能快速收敛,又能满足服务器快速上线的需求.
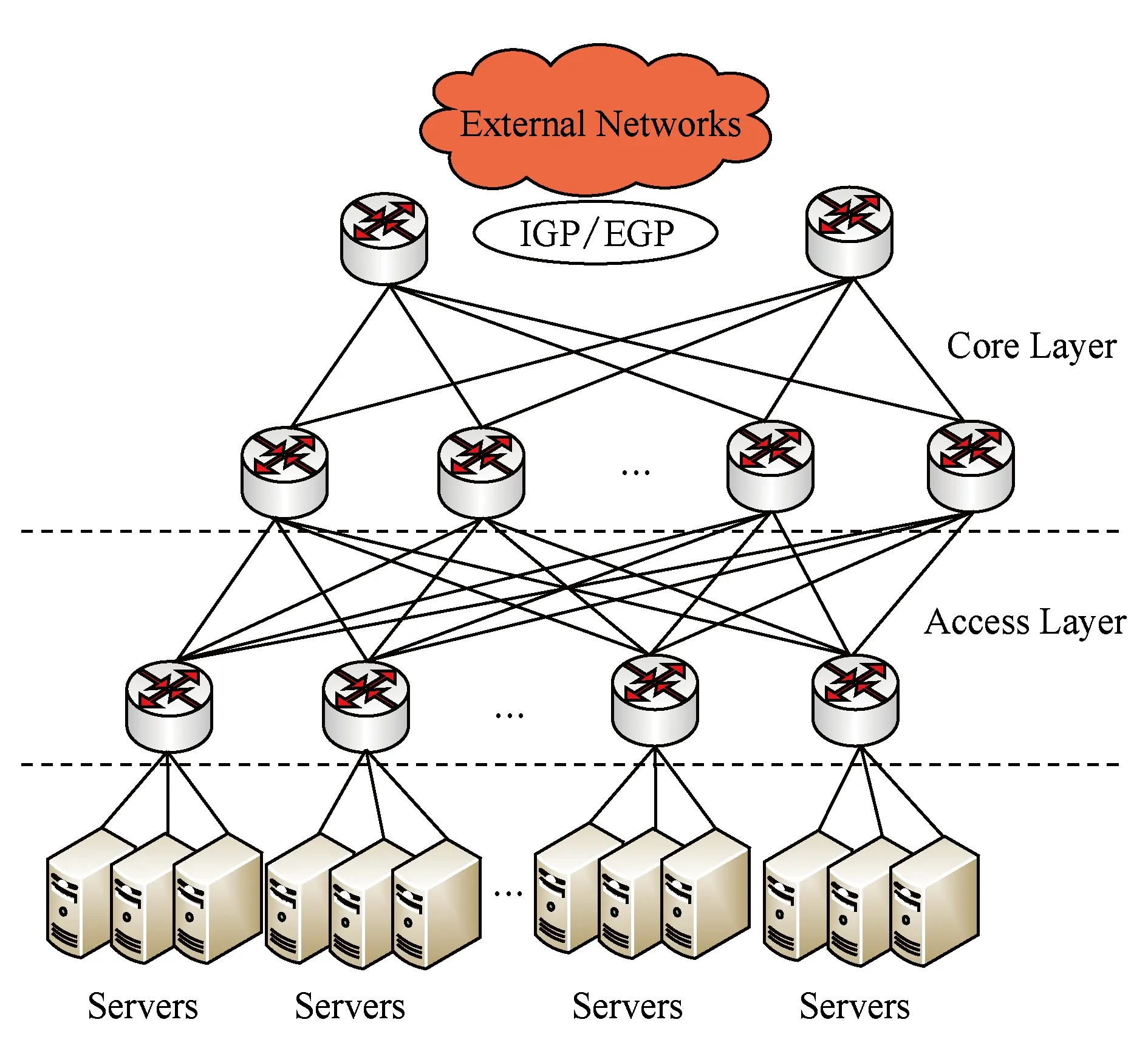
Fig. 2 Flat topology图2 扁平拓扑结构
1.2 数据中心的网络数据
网络数据是进行故障检测、故障定位和流量分析的原始数据,它能够体现出当前网络状态和流量特征,通过对多维度网络数据的分析、统计和计算,建立网络模型,实时监控网络,具体数据分类如表1所示:
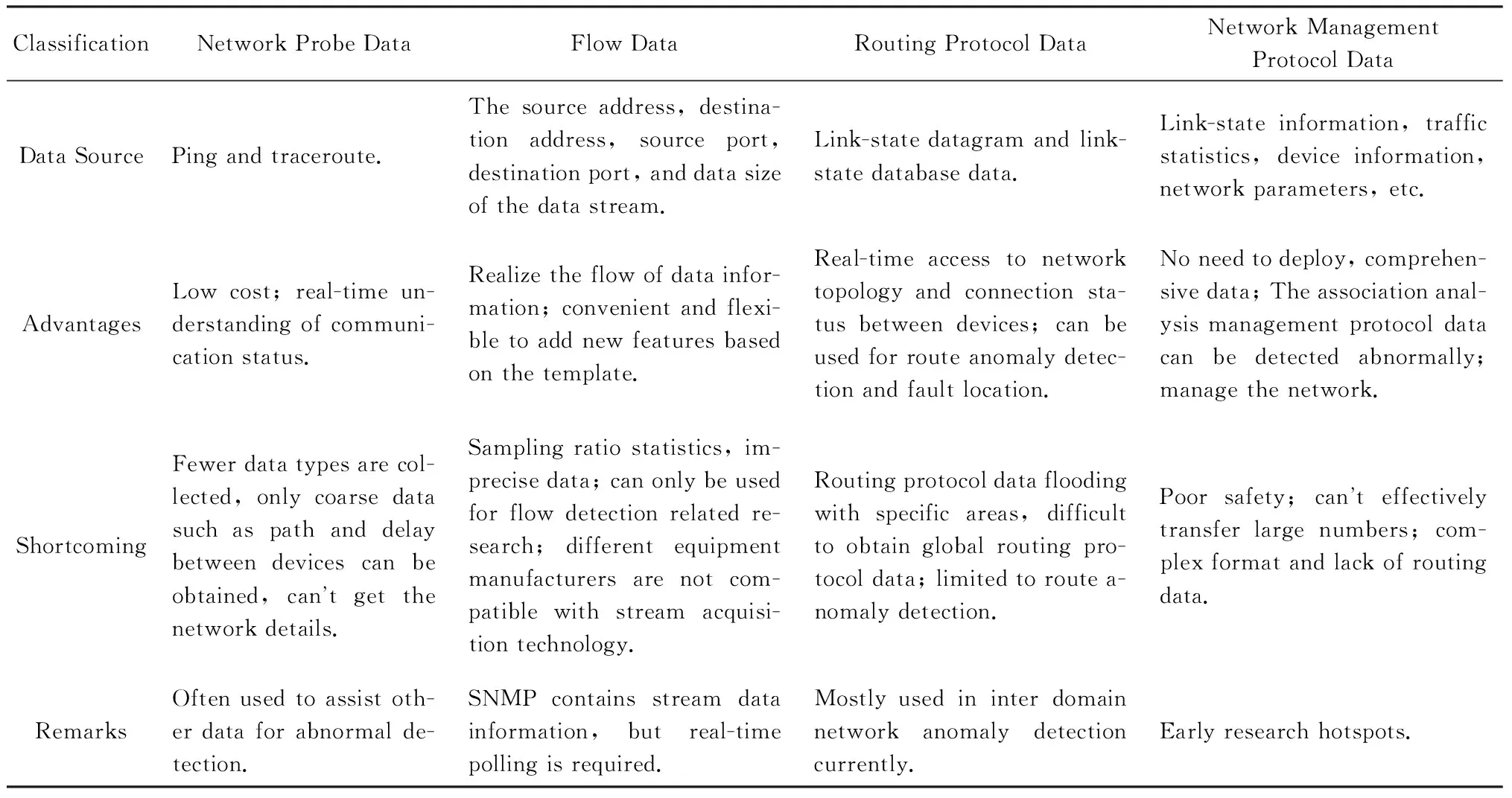
Table 1 Network Data Classification表1 网络数据分类
1) 网络探针数据[3]
2) 流数据
流数据是指通过对流经网络设备的数据包的头部进行分析,采集经过设备的流信息.流数据并不检测流经设备的所有数据包,而是根据采样比进行采样、分析和统计.流数据主要包括数据流的源地址、目的地址、源端口、目的端口和数据大小,通过流数据能够用来检测异常的数据流[4-5].目前成熟的流数据采集技术包括Cisco的NetFlow技术、Huawei的NetStream技术和Juniper的sFlow技术等,NetFlow技术应用范围最广,一共包括V1,V5,V7,V8,V9这5个主要的实用版本.
3) 路由协议数据
路由协议是指通过在路由器之间共享路由信息来支持可路由协议.路由信息通过在相邻路由器之间泛洪,确保所有路由器同步路由信息并进行路由收敛,从而知道到达目的路由器的路径.通过与数据中心内网络设备建立连接关系,就可以采集到域内路由信息并构建网络拓扑和获取设备间链接状态.路由协议数据能够进行异常检测和故障定位,但是难点在于如何获取全网路由信息,利用采集的路由信息检测异常和定位.本文进行异常检测和故障定位的源数据就是数据中心网络中链路状态数据库(LSDB)数据,通过LSDB复原路由表,比对LSDB快照和路由表快照进行检测和监控.
4) 网络管理协议数据
网络管理协议是一种提供给网络管理员用于网络监控的工具,具体包括链路状态信息、网络流量统计、设备信息、网络参数等多维度全方面信息,是进行异常检测中普遍使用的监测数据.由于该类型数据能够提供详细的网络信息,因而通过将不同设备间的网络管理协议数据进行关联分析就能够进行异常检测[6-9].简单网络管理协议(SNMP)是基于TCPIP的网络上使用最为广泛网络管理模型,既可以管理最简单的网络实现基本的管理功能,又满足大型复杂网络的管理需求.SNMP是由一系列协议组和规范组成的,提供了一种从网络设备中收集网络管理信息的方法.
1.3 相关工作
近年来,国内外在路由异常检测及分析方面的研究工作有很多,相关方向的研究、文章有很多.现在数据中心中还没有成熟的路由异常检测和分析工具,在路由异常定位方面相关研究也非常有限.国外的公司和大学如Google,Facebook,AT&T、哥伦比亚大学大学等高校已经对路由检测开展了一些研究,国内清华大学、国防科技大学等大学在协议主动测试和被动测试方面进行了大量的研究和开发,阿里巴巴数据中心和百度数据中心也在进行路由异常检测方面相关研究.从这些研究成果中总结出以下3种路由检测方法:
1) 基于SNMP协议的网络监测系统利用SNMP MIB库提供的网络信息构建网络拓扑和监控端口等,使用trap功能实现异常发现和告警.现在比较成熟产品包括Tivoli NetView和MasterScope等,该类产品优势在于能够实现拓扑构建、网络性能分析和异常告警,但是路由异常功能在异常检测中实现的功能较少,未实现路由异常定位且需要使用日志信息和其他监测工具辅助,增加了网络负担和部署负担.
2) Shaikh等人[10-11]和Zhang等人[12]在IGP(内部路由协议)路由异常检测方面贡献突出,分别阐述了IGP内路由检测方法并进行了实验验证.Shaikh在OSPF协议方面进行大量研究,他首先从运行OSPF协议的大型网络中学习OSPF协议运行行为,主要是对链路状态通告行为的分析.在进行大量实验后,Shaikh开始研究利用OSPF协议构建网络拓扑,通过被动监听网络数据流构建拓扑结构,最后比较了利用OSPF协议构建拓扑和利用SNMP协议构建拓扑在可靠性和实时性上的差异[10],总结出由拓扑结构改变或其他原因产生的网络异常信息,并提出一种OSPF路由监测系统的实现方法.Shaikh等人[10-11]指出该系统能够有效地发现网络中的拓扑异常.但是Shaikh等人[10-11]只是通过协议获得了网络拓扑信息,并只能发现拓扑改变,在功能上和性能上不能完全用来检测路由异常.
3) 在域间路由协议(border gateway protocol, BGP)路由异常监测工作中,以Oregon大学的Route Views项目[13]、RIPE NCC的RIS项目[14]、UCLA的Zhang[15]以及哥伦比亚大学的Al-Musawi等人[16]为代表主要进行域间路由异常检测工作,这些工作主要面向公共的BGP 路由数据服务、BGP路由动态行为的可视化、基本的安全监测服务3个方面.
本文研究与上述研究不同之处主要存在于4个方面:
1) 提出一种新型方法导出数据中心OSPF和ISIS网络内的全网路由信息,为复原路由表提供原始链路状态信息.
2) 利用改进Dijkstra算法复原路由表,提出改进算法并给予理论验证.
3) 相比于Shaikh等人[10-11]、Zhang等人[12]、Al- Musawi等人[16]研究的内容都是路由异常问题,本文研究内容基于数据中心内部路由异常,而不是域间路由异常;与Shaikh等人[10-11]和Zhang等人[12]不同的是不仅仅能够发现路由异常,还能够迅速进行异常源头定位.
4) 除路由异常检测外,利用链路状态数据库实现路由攻击和异常定位.
2 LSAP系统设计
本节主要介绍如何通过LSAP进行路由异常检测.如图3所示系统的主要组成部分.首先通过软件路由器或者开启BGP-LS协议采集网络路由信息,导出IGP协议中的LSDB,由于在每个区域内路由器定期同步链路状态数据库,因而我们只需要采集所有区域而不是所有路由设备的LSDB,采集方案我们优先选择BGP-LS,软件路由器作为备选采集方案,然后根据改进的Dijkstra算法计算路由表(RIB),最后比对LSDB 快照和RIB快照进行快速发现链路状态变化和路由变化等.
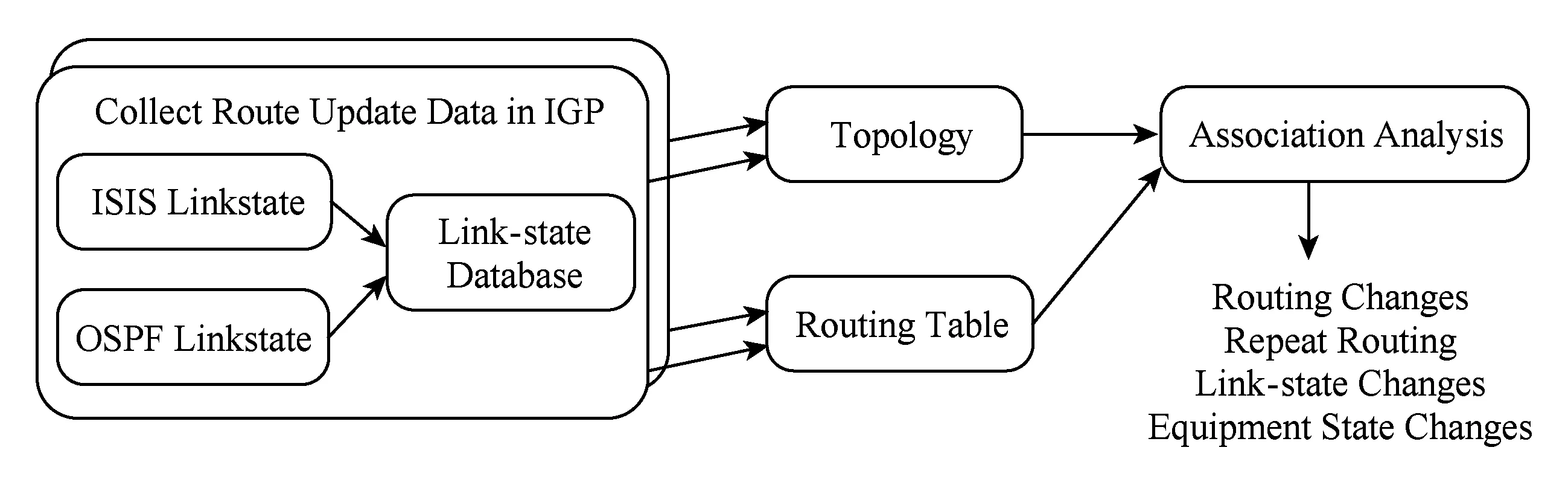
Fig. 3 Anomaly detection process of LSAP图3 LSAP异常检测流程
2.1 LSDB导出
在本文中我们优先选择BGP-LS,软件路由器作为备选采集方案导出LSDB,数据中心网络按区域划分收集.数据中心通常会维护一张网络设备信息表,包括设备名、路由协议类型、区域号、设备型号、设备厂商、部署时间等.在本系统部署之前我们会要求设备厂商提供部署BGP-LS协议的设备型号集合B.设:
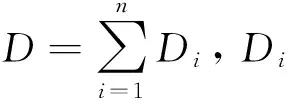
Ii={ISIS第i个区域内路由器集合}=
{Dk|Dk∈R且Dk拥有相同区域号};
I={ISIS区域所有路由器集合}=∪Ii;
Oi={OSPF第i个区域内路由器集合}=
{Dk|Dk∈R且Dk拥有相同区域号};
O={OSPF区域所有路由器集合}=∪Oi.
算法1. LSDB采集算法.
① 遍历所有ISIS区域;
② 遍历判断ISIS区域内设备类型是否属于B;
③ 记录设备的采集类型,1表示采集方案为BGP-LS,0表示采集方案为Zebra的采集方案;
④ 遍历所有OSPF区域;
⑤ 遍历判断OSPF区域内设备类型是否属于B;
⑥ 记录设备的采集类型,1表示采集方案为BGP-LS,0表示采集方案为Zebra的采集方案.
2.2 路由表复原
现存的路由表获取方法大致分为3种:登录路由器CLI收集、厂商提供和网络收集.登录路由器查看往往需要手工辅助,受限于数据中心内路由器数量庞大和不同厂商路由器的路由表格式不同,该方式获取路由表可行性较低;厂商提供往往需要配置专用路由器提供对外输出路由表接口,该方式获取的路由表精确快速,但是价格较为昂贵,非专用路由器无法直接导出路由表数据;网络收集主要是利用网络内泛洪链路状态信息,利用路由计算算法复原路由,该方式性价比较高,提供较为准确的路由表,速度上仅低于专用路由器.
在导出的LSDB可以获取各区域中的拓扑链接关系以及连接权值Metric,即可形成赋权图G=(V,E,W),设节点v0,v1,…,vm∈V,边e1,e2,…,en∈E,W为边(i,j)∈V对应的wi j的集合.加权图用邻接矩阵A表示,规定:若vi和vj之间没有链接,则ai j=∞;若vi和vj之间存在链接,则ai j=wi j,即为相连路由器之间Metric值;若i=j,则ai j=0.在用链路邻接矩阵是指行到列之间路径条数.在用链路邻接矩阵U表示,规定:若vi和vj之间没有链接,则Ui j=0;若vi和vj之间存在链接,则Ui j表示相连路由器之间Metric为ai j的条数.
2.2.1 Dijkstra算法的基本思想
Dijkstra算法是指在一个赋权图查询2个指定顶点vi和vj之间的最短路径.该算法是一个求解最短路问题的算法,不仅能够找到最短的(vi,vj)路径,而且可以给出vi到G中所有顶点最短路径.
最短路径的计算步骤如下:
设S表示已求得的从vi出发的最短路径的终点集合;
m阶标识矩阵R,存储已求得的从vi到其他顶点vj的所有最短路径上的此顶点的前驱顶点.
① 初始化S和R,S={vi},R=(ri j).
② 选择vm,使得:
aim=min {aik|vk∈V-S},令S=S∪{vm}.
③ 修改从vi出发到集合V-S中所有节点vk的最短路径长度.
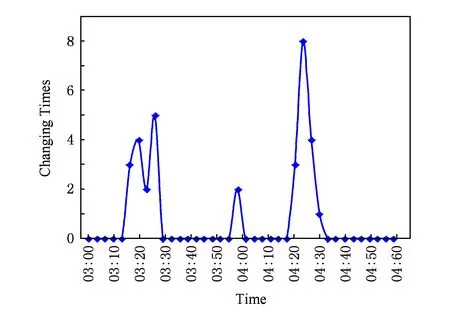
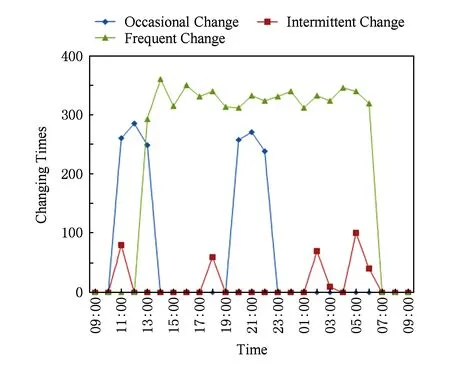
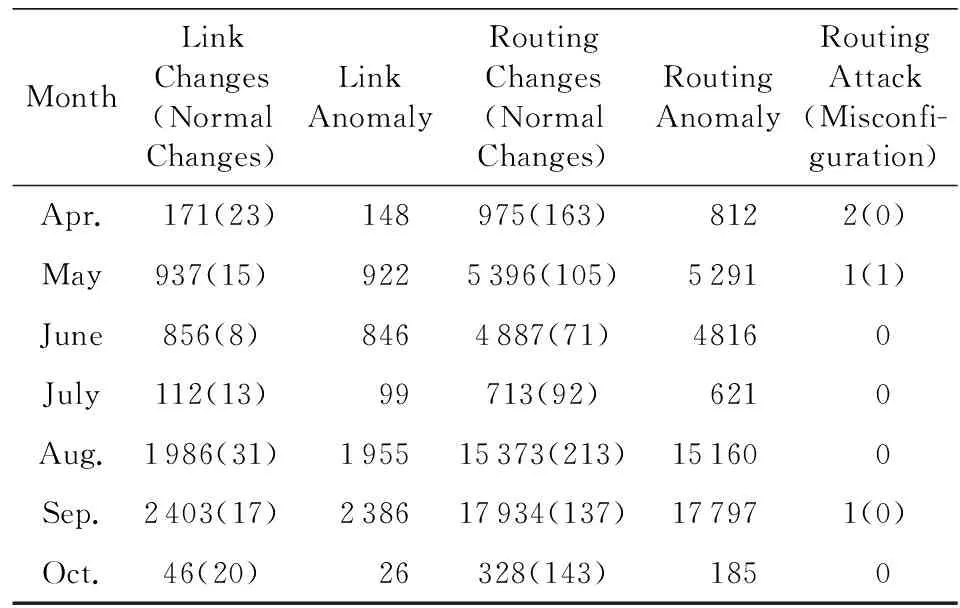
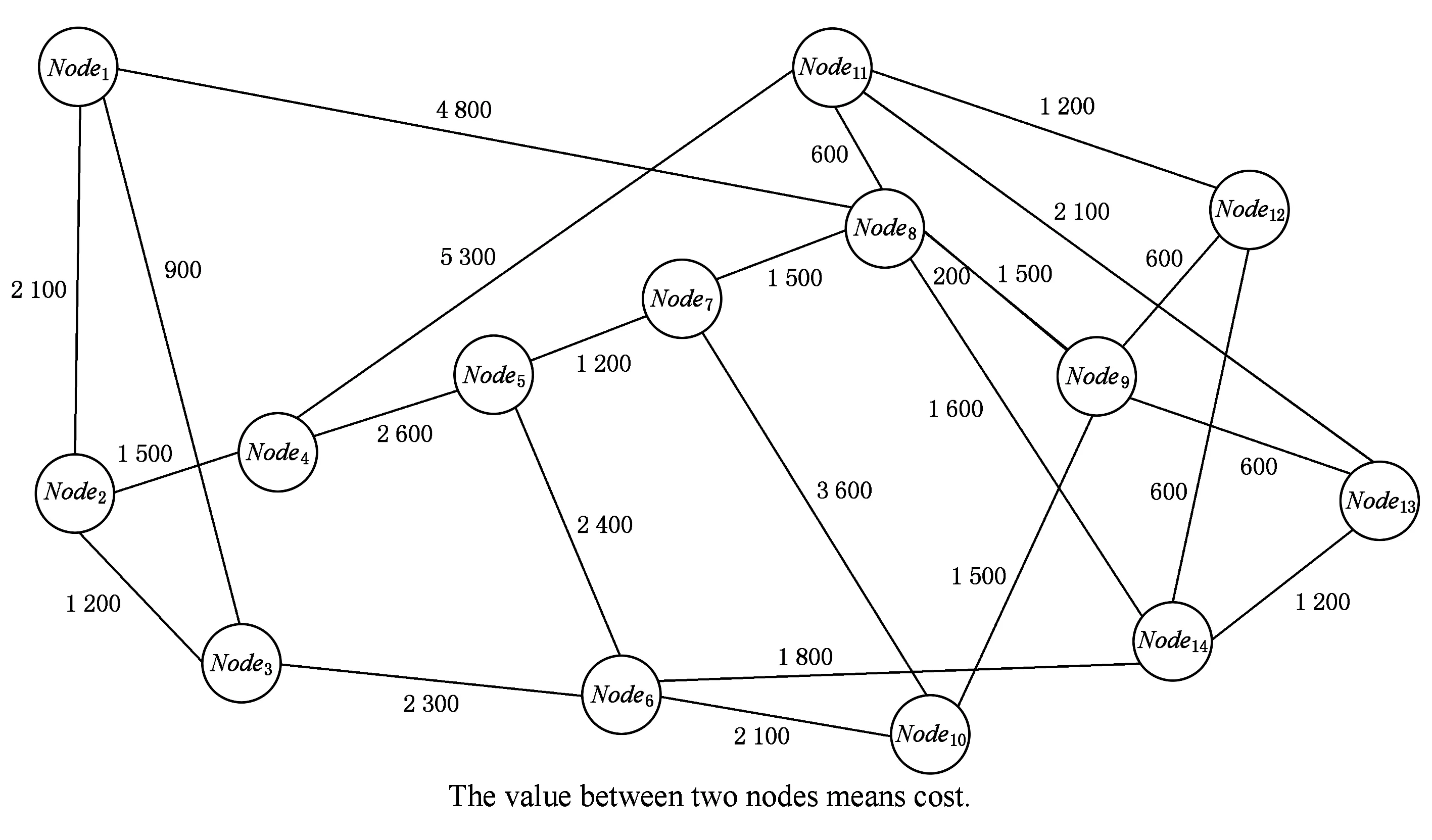
如果:amk> 0且aim+amk 则修改为aik=aim+amk. ④ 重复操作②③共n-1次,即可求得从vi到其余各定点vj的最短路径长度. 但是,Dijkstra算法只能求得节点间一条最短路径,不能保存所有最短路径且②③操作需重复n-1次,本文首先优化Dijkstra算法,解决大规模网络节点和链路过多路由计算时间过长的问题. 2.2.2 Dijkstra算法的优化 在网络中心的网络模型有2个特点: 1) 由于数据中心网络配置现状,同一层次路由器间接口链路的Metric值通常是相等的(存在不相等情况); 2) 鉴于特点1和数据中心冗余链路的存在,节点之间总度量相等链路具有多条;从单节点到其余节点总度量相等的个数有多个. 优化采取的方案是: 优化的目标是提高集合S的效率,最大程度地加快增加S中与最短距离路径相关的顶点的计算和减少S中与最短距离路径无关的顶点的计算. 选择新节点加入S时,不仅只选择一条最短路径的节点加入S,而是将最短路径相等的所有节点加入S; 选择新节点加入S时,不仅只选择离vi最近的顶点加入集合S,而是向着从vi到vj最短路径不断逼近的目标而选择顶点加入集合S. 标识矩阵R用来存储从vi到其余各顶点的所有最短路径的此顶点的前驱顶点,即若从vi到vj的一条最短路径为vi,v2,v4,…,vj,在此路径中,v2是v4的前驱顶点,则R[2][4]=1,否则R[2][4]=0. 优化最短路径的计算步骤如下: ① 初始化S和R,S={vi},R=(ri j). ② 选择aim相等的所有节点vm,S′={vm}且S′⊆V-S使得aim+hopsm×metricmin=min {aik+hopsk×metricmin|vk∈V-S},令S=S∪S′. hopsm:vm至vj节点之间的跳数,目前数据中心内多种业务并存,通过即时通信客户端运行主动探测工具ping和traceroute命令获取数据中心内部节点间时延数据和跳数; metricmin:区域内最小Metric值,相同区域内Metric值相差不大. ③ 修改从vi出发到集合V-S中所有节点vk的最短路径长度. 如果:amk>0且aim+amk 则修改为aik=aim+amk. ④ 重复操作②③直至求出最小ai j,即可求得从vi到其余各定点vj最短路径长度. ⑤ 将最短路径按照前驱节点规则添加到R中. 从优化最短路径的计算步骤中可以发现,优化算法是相似于Dijkstra算法的,但对顶点的选择是不同的.在Dijkstra算法中,不断选择离vi最近的一个顶点加入到集合S,而没有考虑最短路径的顶点个数和把vi,vj同时联系起来考虑.在优化算法中,向着vi和vj最短路径的不断逼近的目标而选择顶点加入集合S中,因此,在集合S包含的是在vi和vj最短路径局部范围内的部分节点,而并不计算全部节点.在这种情况下,优化算法的集合S和②③迭代次数相较Dijkstra算法的集合S和②③迭代次数小得多、少得多. 2.2.3 Dijkstra改进算法正确性证明 Fig. 4 Shortest path graph from vi to vj图4 vi到vj最短路径 在改进算法中vj加入S时: 1) 若mqS时 已求得最短距离A(vi,mq)+(hops(mq,vj)×metricmin)≥A(vi,vj)+0=A(vi,vj),由于hops(mq,vj)×metricmin≤A(mq,vj)=a(mq,vj),因此可以推出A(vi,vq)+a(mq,vj)≥A(vi,vj). 2) 若mq∈S时 当mq加入S时A(vi,vj)=min {A(vi,vj),A(vi,mq)+A(mq,vj)}=min {A(vi,vj),A(vi,mq)+a(mq,vj)},记为A1(vi,vj). 由Dijkstra改进算法可知vp加入S时修改了A(vi,vj)值,因而当vp加入S时A(vi,vj)=min {A(vi,vj),A(vi,vp)+A(vp,vj)}=A(vi,vp)+a(vp,vj),A(vi,vj)即为改进算法求取的最终vi到vj的最短距离. ① 当mq先于vp加入S时,vp加入S时修改了A(vi,vj),A(vi,vj)=A(vi,vp)+A(vp,vj) ② 当mq后于vp加入S时,vp为最短路径的最后节点,mq加入S时并未修改A(vi,vj),A1(vi,vj)=A(vi,vj)≤A(vi,mq)+a(mq,vj). 综上所述,不论mq何时加入S中,可得 A(vi,vj)≤A(vi,mq)+a(mq,vj). (1) 根据假设在vi到vj存在的最短路径为vim1m2m3…mqvj,最短路径为A′(vi,vj). A′(vi,vj)=A′(vi,mq)+A′(mq,vj)= (2) 因为改进算法求出最短路径为A(vi,vj),根据假设已知最短路径为A′(vi,vj),因而 A′(vi,vj) (3) 将式(1)(2)带入式(3),可以推出: A′(vi,mq)+a(mq,vj)=A′(vi,vj) 可得: A′(vi,mq) (4) 根据式(4)可以推出在优化算法中mq未求得正确的最短路径,还存在另外一条距离小于最短距离A(vi,mq)的更短路径.因此根据反证法假设可以推出未正确求出正确vi到vj最短路径的原因在于未求出正确vi到mq最短路径.将mq替换vj重复上述证明可以推出未正确求出正确vi到vj最短路径的原因在于未求出正确vi到mq-1最短路径,以此类推:改进算法未求出正确vi到m2最短路径的原因在于未求出正确vi到m1最短路径.根据Dijkstra算法已知节点vi与节点m1是直接相连,因而d(vi,m1)=a(vi,m1),在改进算法中节点vi与节点m1最短距离是正确的. 因此与假设相矛盾,假设是不成立的,证明了本文Dijkstra改进算法是正确的. 本文重点关注路由异常的检测,主要涉及路由黑洞攻击、链路异常和路由异常,如表2所示: Table 2 Network Anomaly Classification表2 网络异常分类 2.3.1 路由黑洞攻击检测算法 路由黑洞攻击是指在区域网络的路由器中注入恶意路由,恶意路由是由误配置或者网络攻击造成的,当恶意路由最终扩散至所有区域路由器后,发往某个特定网络的数据包的传输流向将被恶意更改,数据将被发送到黑客指定的目的地,这个目的地就像“黑洞”一样将发往某个特定网络的数据包吸引过来,因此称这种攻击为“黑洞攻击”. 路由黑洞攻击检测方法是采集所有路由器宣告网段(宣告网段是指路由器对外宣告直接相连的网段,以网络子网号形式表示),正常情况下所有路由器宣告网段是具有唯一性的,否则会导致“黑洞”,因而通过判断宣告网段的包含关系可以检测出路由黑洞攻击. 具体算法如下所示: 算法2. 路由黑洞攻击检测算法. 设路由器宣告网段递增排序为p1,p2,…,pq,t0代表路由更新时间(t0非固定值). ① 遍历p1,p2,…,pq,初始化i=2,标识路由p′=p1以及集合S; ② 取出pi,判断pi是否是p′子网段,若是则pi加入S中,i=i+1跳至②循环执行;否则判断S个数,card(S)≠0时将p′加入S,存储S集合至消息队列同时清空S; ③ 判断i+1≥n,是则跳至步骤④,否则p′=pi+1,i=i+2跳至步骤②执行; ④ 推送消息队列至管理员. 算法3. 算法2步骤②中判断子网包含关系算法. 函数netXInNetY(longx,intxmask,longy,intymask) ① 验证子网关系,ymask>xmask时返回否; ② 根据x和xmask得出子网号xnet; ③ 根据y和ymask得出子网号ynet; ④xnet与ynet进行与运算,与运算结果即为包含关系. 2.3.2 链路异常检测算法 本文提供一种基于路由的链路状态检测方法,通过LSDB快照快速发现链路状态变更,主动上报中央控制端. 链路异常检测方法是通过比对路由更新信息前链路状态和路由更新信息后链路状态进行快照比对,即可得出链路变化(链路权值变化和链路连接变化). 具体算法如下所示: 根据2.2.2节中可知,A和U表明时刻t加权图邻接矩阵和在用链路邻接矩阵,A′和U′表明时刻t′加权图邻接矩阵和在用链路邻接矩阵.在用链路邻接矩阵表示行节点到列节点之间路径条数.t′-t代表路由更新时间. 算法4. 链路异常检测算法. 1) 初始化A和U,A′和U′; 2) 计算链路改变矩阵Achange=A′-A, 3) 计算用链路邻接矩阵Uchange=U′-U, 4) 判断achange和uchange: ①achange>0,uchange>0:权值增加且使用链路增加; ②achange>0,uchange<0:权值增加且使用链路减少; ③achange>0,uchange=0:权值增加且使用链路未改变; ④achange<0,uchange>0:权值减少且使用链路增加; ⑤achange<0,uchange<0:权值减少且使用链路减少; ⑥achange<0,uchange=0:权值减少且使用链路未改变; ⑦achange=0,uchange>0:权值未改变但使用链路增加; ⑧achange=0,uchange<0:权值未改变但使用链路减少. achange>0说明链路所在节点权值增加,可能引流至其他节点;achange<0说明链路所在节点权值降低,可能引流至该链路相连节点. 2.3.3 路由异常检测算法 路由异常包括设备连接不通和路由频繁变化2种情况. 设备连接不通检测方法是采集数据中心内所有区域的链路状态数据库,画出完整的网络拓扑图,通过改进的Dijkstra算法计算端到端的路由表,从而得出以自身为根节点的无环路最短路径树,通过判断其他节点是否在最短路径树上即可判断设备连接状态:所有在最短路径树上的节点为可达节点,不在最短路径上节点为不可达节点. 由于数据中心内路由设备配置和设备连接关系是相对稳定的,因此网络路由表是稳定的.对于维护人员来说,未主动修改路由器配置的路由变化就属于异常变化,是需要检查排除故障.路由变化是指路由信息更新后,由于节点间连接关系和权值改变导致路径或者路径开销值发生改变. 路由异常与路由定位检测方法是首先通过快照比对设备路由更新前后标识矩阵R,从而获取路由信息更新后设备到其他节点的前驱节点变化,根据前驱节点变化即可获得设备到其他节点的路径变化(包括路径增加和路径减少),其次计算比对更新前后的完整路径和总开销值,最后通过关联链路变化和路径变化关系发现路由变化和进行路由定位. 算法5. 路由异常检测算法. 1) 初始化矩阵标识矩阵R+,R-为0. 2) 遍历i(1≤i≤n),n为节点个数并初始化,临时矩阵tmpi=0. tmpi[a][b]=0前驱节点没有变化,时刻t,va是vb的前驱节点;时刻t′,va也是vb的前驱节点;或者时刻t,va不是vb的前驱节点;时刻t′,va也不是vb的前驱节点; tmpi[a][b]=1代表时刻t,va不是vb的前驱节点;时刻t′,va是vb的前驱节点;tmpi[a][b]=-1代表时刻t,va是vb的前驱节点;时刻t′,va不是vb的前驱节点. 4) 遍历矩阵tmpi列,从第j(初始化j=1)列开始. 当矩阵tmpi中第b列值只有0和-1值时,该变化类型设为2,可以确认的是t′时没有增加路径,只是减少了路径,引起该类型路由变化原因是由于保留链路或减少链路的Metric减小增加造成的;判断减少链路∑|achange|<任一保留链路∑|achange|,是则所有保留链路中{achange|achange<0}造成路由变化;否则减少链路{achange|achange>0}造成路由变化;判定变化原因后,记录链路独有变化详情; 当矩阵tmpi中第b列同时存在±1值时,该变化类型设为4,假设q为增加路径的前驱节点,判断增加链路∑|achange|<减少链路∑|achange|,减少链路中{achange|achange>0}造成路由变化;否则增加链路中{achange|achange<0}影响路由变化;判定变化原因后,记录链路变化详情. 注:增加链路有多条时,或减少链路有多条时,该算法仍然适应. 5)j=j+1;判断j>n,是跳至步骤6,否则判断j是否在步骤4已扫描,是跳至第步骤5,否则跳至步骤4. 6)i=i+1;判断i>n,是跳至步骤7,否则跳至步骤2. 7) 根据路由变化对象统计各个设备链路状态带来的路由变化,影响路由数量由多到少依次排列,并通过消息提示网络管理员. 通过上述算法将链路状态变化和路由变化相关联,给出整个网络变化信息,并以列表的形式提供给网络管理员,当发现路由异常时,能够进行异常定位,从而能够快速恢复网络. 我们部署LSAP到多业务的数据中心内,该数据中心业务主要包含即时通信、电商业务、金融业务、搜索、广告、云计算等多业务.主要验证了系统路由异常检测在数据中心效果. 为验证改进版Dijkstra算法的可行性,分析了与传统Dijkstra算法运行时间对比,本文针对数据中心内不同拓扑集合进行了实验.实验数据如表3所示,共有5组实验数据,数据集的网络节点数在592~12 965之间,弧段数在916~32 658之间,节点数和弧段数之比在0.3~0.7之间.实验从每个数据集合中随机选取100组源点和终点,测试不同网络节点数量和弧段数量下传统Dijkstra算法和本文算法运行时间对比,如表3所示: Table 3 Algorithm Performance Statistics表3 算法性能统计 为了测试算法的效率,分别采用不同的节点数和弧段数对比传统Dijkstra算法和改进Dijkstra算法最短路径计算时间.我们发现当节点数(592和1 980)较少时,改进Dijkstra算法计算时间比传统Dijkstra算法的计算时间长一点,原因在于改进Dijkstra算法的初始化时间会增加且添加了优化顶点选择处理;当节点数(≥3 517)增加时,我们会发现改进Dijkstra算法的计算时间相比于传统Dijkstra算法少很多;节点数和弧段数越多,改进Dijkstra算法的改进效果越明显.本文所论述的改进算法在传统Dijkstra算法的基础上加以改进,优化最短路径的计算过程,减少了算法的执行时间. 该数据中心包括5 000 000台以上服务器、15 000台路由设备并运行9 800多应用程序.服务器操作系统主要采用的是自主研发的Linux系统,每台服务器平均CPU16核,内存80 GB.路由设备涉及Cisco、华为、H3C、中兴设备等,数据中心网络架构以3层网络架构为主,主要架构如图5所示: 在本系统从2016年4月开始试运行并持续运行半年多时间,主要测试了2个区域数据中心间骨干网络(图5中大矩形代表区域)和主业务区域网络(图5中小矩形代表区域).骨干网络主要负责8个不同地区的数据中心之间的数据传输,共包括156台高性能路由器,不同地区间路由器相连通过专线连接;主业务区域网络涉及电商业务,本文调研的华东机房涉及主机4 992台,机房路由器和接入层路由器共计58台. 在本节中将主要介绍在数据中心内测试的详细数据,包括数据中心内不同区域路由变化详情、详细数据和LSPLSA异常变化的规律. 3.3.1 路由变化详情 图6是通过LSAP生成的路由更新信息变化图,显示了运行ISIS协议的骨干网络与运行OSPF协议的主业务区域网络6个月的域内路由信息变化量,给出了该数据中心内路由变化的概括图.从图6我们可以看出,在大部分时间内骨干网络的LSP变化还是维持在一个较低的水平上,但是在5月底6月初和8月底9月初时路由变化数量增长较快,最高能够超过2 000,需要说明的是当网络进行扩容或压缩时,路由变化数会有提升,但是通常不会大幅度提升路由变化数目,路由攻击和路由交换机端口的不稳定(如频繁的UPDOWN)通常是引起路由更新变化频繁的根本原因.路由更新变化数量代表网络收敛速度,变化量越小代表网络越稳定,变化量越大则代表网络更多时间处于抖动之中. ASR-1.DC8在2016-05-31T03:00:00-05:00:00路由变化,通过图7我们可以发现ASR-1.DC8的链路是间歇性变化的,其中 (03:15:00-03:30:00),(03:54:00-04:03:00),(04:18:00-04:33:00)三个时刻LSA变化最为频繁,经过与网络管理员的确认,发现是由于该设备的上线时间较短,查看该设备当时日志文档并未发现端口频繁UpDown的报告,最终发现是连接该端口物理连线接触问题造成该情况的产生. Fig. 7 Number of changes of LSA on the device ASR-1.DC8图7 设备ASR-1.DC8的LSA变化个数 表4列出了链路状态变化的典型类型,包括链路变化和Metric变化.链路UpDown如表4第2~6行数据所示,↑代表添加路由,↓代表取消路由,图示可以看出在03:24:03时序列号为0x0001781f的LSA宣告路由42.120.244.430;在下一时刻更新的LSA报文(序列号+1)可以看出取消宣告42.120.244.430,该端口关闭;03:24:11时该端口重新开启宣告42.120.244. 430,端口频繁的开启关闭导致对外重复宣告和取消路由42.120.244.430.链路连接变化如表4第7,8行数据所示,在03:24:03时该路由器与ASR-14.DC8是相连接的,在03:24:06时刻路由器断开与ASR-14.DC8的连接,建立了与ASR-21.DC8的连接,链路连接变化直接导致路由拓扑的变化. Table 4 Schematic Diagram of Link-State Change表4 链路状态变化示意图 “↑”means adding routing; “↓”means canceling routing. Metric变化通常代表链路的开销值,↑代表开销值增加,↓代表开销值降低,如表4所示03:28:50时宣告140.205.19.8030网段的端口Metric从2 000增加10 000;同样,3:30:15时宣告61.237.112.830网段的端口Metric从10 000降低到1 000.Metric变化和链路变化会触发Dijkstra算法计算最短路径树,Metric变化通常是由网络配置触发的,链路变化的原因则比较多,设备老化、网线连接、网络配置、路由攻击都是造成链路变化的原因,链路状态的频繁变化通常是由于设备老化、网线接触或路由攻击等造成端口频繁UpDown的,因而通过我们的分析结果就可以辅助网络管理员查找链路状态不稳定的设备,进行路由异常发现、定位和排除. Fig. 8 Types of changes of LSP and LSA 图8 LSPLSA变化类型 在LSAP统计的变化规律中我们发现3种类型的变化:偶尔变化、间歇变化和频繁变化.经统计,偶尔变化是所有路由器上最普遍的变化类型,在图8所示偶尔变化中1台路由设备的典型变化,我们会发现该路由器在1 d中主要在2个时间区间有LSPLSA变化,其他时间内基本没有任何变化,变化时间主要在10:00:00-13:00:00和19:00:00-22:00:00这2个时间段内.对于无固定时间段内的偶尔变化类型的路由器,通过查看设备日志信息发现大多数是由于端口宣告开启和关闭造成,造成端口偶尔开启关闭的原因是多样的,如设备故障、线路老化、路由攻击等.对于图示中具有明显时间痕迹的变化,我们发现10:00:00-13:00:00和19:00:00-22:00:00正是该数据中心访问量最大的时间,且设备日志并未记录端口故障信息,把线路老化原因排除后,通过netflow数据发现该时间段内都是数据流通过该设备的顶峰时间和snmp记录的端口丢包率发现引起LSPLSA变化的原因是由于网络拥塞造成的. 对于间歇变化的路由器,我们会发现这些路由器的共性是变化不规律、变化量和变化数不定、间歇变化且从某时刻间后持续的间断进行变化.该类型变化通常是由于设备或线路老化造成端口不稳定引起的.在图8所示频繁变化路由设备的典型例子,通过该折线图我们可以看出该路由器在1 d时间内是持续变化的,可以看出该路由器以平均320次h的频率持续宣告路由端口状态改变.对于该类型的路由器我们发现主要是由于链路问题和网络误配置(如设备ID设置相同)造成的. 在本节中将主要介绍通过LSAP在数据中心异常检测的结果,通过本节内容能够明确路由变化的根本原因,从而辅助网络管理员修复异常或故障. 3.4.1 异常检测 表5展示了通过LSAP在骨干网中的统计数据,主要包括链路变更数、链路异常、路由变更、路由异常和路由攻击事件等.如4月份统计数据,171 (23)代表链路变更数为171次,包括连接关系改变、端口开启关闭、Metric变化等;23代表是由网络管理员为网络管理需要而人为配置造成的状态改变,属于正常变更,异常链路变更数为171-23=148.975(163)代表路由变更数为975条,路由变化既包括路径改变也包括链路开销值改变;其中163代表由人为配置造成造成的路由变化,则异常路由变更数为975-163=812,其中4月份骨干网总共遭受了2次路由攻击,由网络误配置造成的路由攻击记录为0,从所有记录中我们可以看出数据中心内部由于防火墙和流量清洗中心的存在,数据中心遭受外界直接路由攻击的数量还是非常少的,绝大多数的路由变化是由于内部设备引起的. Table 5 Link-Change and Route-Change Statistics of 同时我们统计每条链路异常导致的路由异常,具体信息如表5所示.链路变更'指的是对路由产生影响的个数,对路由影响既包括路由路径也包括链路开销值.从表5推算得出60.1%的链路变化并未引起路由变化,39.9%的链路变化'引起了路由变化,平均影响一半区域节点. 3.4.2 异常定位 在本节,通过利用14个节点的NSFNET网络实例来验证LSAP算法是如何进行异常定位的.图9是NSFNET原始拓扑加权图,图10是路由更新后加权图.下面我们将具体说明异常定位过程,实例是根据节点4到其他节点的最短路径的变化情况推出路由变化,根据Dijkstra算法可算出图9,10所示拓扑节点4到其他节点的最短路径,如表6所示. Fig. 9 Initial network topological graph of NSFNET图9 NSFNET网络初始拓扑图 Fig. 10 Network topological graph of NSFNET after updating图10 路由更新后NSFNET网络拓扑图 DestinationShortestPathinFig.9CostofFig.9ShortestPathinFig.10CostofFig.1014→2→136004→2→14→2→3→1360024→215004→2150034→2→327004→2→3270054→512004→5260064→5→636004→2→3→64→5→6500074→5→724004→5→7380084→5→7→839004→5→7→8530094→5→7→8→954004→11→12→96700104→5→6→104→5→7→1057004→2→3→6→104→5→6→107100114→1139004→115300124→11→1251004→11→126500134→5→6→7→8→9→134→11→1360004→11→12→9→137300144→5→6→144→5→7→8→1445004→5→6→146800 根据2.3节路由异常检测算法,可以计算出tmp4: 遍历矩阵tmp4列向量,初始化j=1. 与第2列相同,第3列无变化,则j=j+1=4. 第7,8列与第5列相同,新增路由变化对象唯一区别在于影响路由不同,分别为4→7,4→8;j=j+1=6,跳至步骤4. 第9列存在±1,既新增1条路由,又减少1条路由.新增路径4→11→12→9和减少路径4→5→7→8→9,经计算增加链路∑|achange|=1 800和减少链路∑|achange|=1 400,增加链路∑|achange|>减少链路∑|achange|,则可以判定引起该类型路由变换是由增加链路中{achange|achange<0}即a12,9变小造成的.路由变化对象链路:12-9,影响路由:4→9,Metric变化:是,变化类型:4;j=j+1=10,跳至步骤4. 第10列只有0和-1值,减少路径4→5→7→10,则减少链路∑|achange|=1 700;选择保留路径4→5→6→10,则保留链路∑|achange|=1 400;减少链路∑|achange|>保留链路∑|achange|,则可以判定引起路由变换原因是由于减少链路{achange|achange>0}即a45,a7,10变大造成的,由于a45非独有性变化因而路由变换根本原因是由a7,10造成的.路由变化对象链路:7-10,影响路由:4→10,Metric变化:是,变化类型:2;j=j+1=11,跳至步骤4. 第11,12列与第5列相同,新增路由变化对象唯一区别在于影响链路:4-11,影响路由分别为4→11,4→12;j=j+1=13,跳至步骤4. 与第10列相同,第13列只有0和-1值,减少链路∑|achange|<保留链路∑|achange|,则可以判定引起路由变换原因是由于保留链路{achange|achange<0}即a12,9变小造成的.路由变化对象链路:12-9,影响路由:4→13,Metric变化:是,变化类型:2;j=j+1=14,跳至步骤4. 与第10列相同,第14列只有0和-1值,路由变化对象链路:6-14,影响路由:4→14,Metric变化:是,变化类型:2;j=j+1=15,j>14退出. 路由变化对象列表如表7所示: Table 7 Association Table of Link-change and Route-change表7 链路变化与路由变化关联表 根据统计结果可以看出节点4,5之间链路变化影响范围最为广泛,影响到4个节点,由于该链路变化,导致3条路由总开销值变化和1条路由路径变化;节点4,11和12,9之间影响了2个节点路由,其余节点只影响了1个节点路由.在数据中心,我们经常会遇到2点之间访问延迟增大,通过2.3节路由异常检测和定位算法就能够给出延迟增大的根本原因.假设4节点为网络访问入口,14为核心业务相连路由器,业务方报告业务访问延迟,请求网络管理员进行排查,此时网络管理员只需要从路由变化对象中提取影响路由4-14的变化信息即可,我们发现变化类型为2,说明路径变少了,变少的根本原因是节点6与节点14间Metric减少了100.想要恢复路由,只需要重设Metric值即可. 通过表7我们能够清晰地掌握每条链路异常变化带来的网络变动详情,而不是简单地获知网络变化数目,在LSAP试运行期间能够有效地帮助网络管理员分析每条链路变化,进行路由异常检测和异常定位. 众所周知,数据中心路由异常、路由抖动普遍存在,路由更新频繁,但是缺乏有效的方法监控,发现异常后无法进行故障定位.本文中,我们提出了一种基于LSDB的数据中心网络分析器LSAP,不仅通过被动的搜集路由更新报文获取拓扑变化,而且通过改进的Dijkstra算法快速计算路由表,统计分析所有路由变化、关联拓扑变化与路由变化,先于业务发现网络故障、路由攻击.LSAP对网络改动很少,被动搜集数据不影响网络自身稳定性,因而适合于对稳定性要求较高的数据中心部署. 致谢感谢中国科学院国有资产经营有限责任公司对本文的大力支持!感谢华为公司的曹政博士对本论文的技术指导! [1]Bhattacharyya D, Kalita J. Network anomaly detection:A machine learning perspective[J]. Network Anomaly Detection, 2013, 45(45): 455-463 [2]Li Dan, Chen Guihai, Ren Fengyuan. Data center network research progress and trengs[J]. Chinese Journal of Computers, 2014, 25(7): 87-89 (in Chinese)(李丹, 陈贵海, 任丰原. 数据中心网络的研究发展与趋势[J]. 计算机学报, 2014, 25(7): 87-89) [3]Zeng Hongyi, Kazemian P, Varghese G, et al. Automatic test packet generation[J]. IEEEACM Trans on Networking, 2014, 22(2): 554-566 [4]Hofstede R, Celeda P, Trammell B, et al. Flow monitoring explained: From packet capture to data analysis with netflow and IPFIX[J]. IEEE Communications Surveys & Tutorials, 2014, 16(4): 2037-2064 [5]Balabine I, Velednitsky A. Method and system for confident anomaly detection in computer network traffic: EU, EP3138008[P]. 2017-03-08 [6]Kim Y I, Park S J, Kim Y J, et al. Development of AMI NMS (network management system) using SNMP for network monitoring of meter reading devices[J]. KEPCO Journal on Electric Power and Energy, 2016, 2(2): 259-268 [7]Jubinville J, Teachman M, Anderson D. Energy monitoring system using network management protocols: US, EP2186258[P]. 2010-05-19 [8]Sonawane V R, Singh L L, Nunse P R, et al. Visual monitoring system using simple network management protocol[C]Proc of the 11th Int Conf on Computational Intelligence and Communication Networks. Piscataway, NJ: IEEE, 2015: 197-200 [9]Ahmed M, Mahmood A N, Hu J. A survey of network anomaly detection techniques[J]. Journal of Network & Computer Applications, 2016, 60: 19-31 [10]Shaikh A, Goyal M, Greenberg A, et al. An OSPF topology server: Design and evaluation[J]. IEEE Journal on Selected Areas in Communications, 2006, 20(4): 746-755 [11]Shaikh A, Greenberg A. OSPF monitoring: Architecture, design and deployment experience[C]Proc of the 1st Conf on Symp on Networked Systems Design and Implementation. Berkeley, CA: USENIX Association, 2004: 5-5 [12]Zhang Shu, Kobayashi K. Rtanaly: A system to detect and measure IGP routing changes[C]Proc of the 5th Int Workshop on IP Operations and Management. Berlin: Springer, 2005: 162-172 [13]Mayer D. University of oregon route views project[EBOL]. Eugene, Oregon: University of Oregon, 2005 [2017-03-17]. http:www.routeviews.org [14]Axel P. RIPE RIS project[EBOL]. Amsterdam, Netherlands: RIPE Network Coordination Centre, 2002 [2016-09-30]. http:data.ris.ripe.net [15]Lad M, Massey D, Pei D, et al. PHAS: A prefix hijack alert system[C]Proc of Conf on USENIX Security Symp. Berkeley, CA: USENIX Association, 2006: 153-166 [16]Al-Musawi B, Branch P, Armitage G. BGP anomaly detection techniques: A survey[J]. IEEE Communications Surveys & Tutorials, 2017, 19(1): 377-396 XuGang, born in 1988. PhD candidate, engineer. His main research interests include datacenter networks, electronicoptical hybrid network and SDN. WangZhan, born in 1986. PhD. His main research interests include computer architecture, high performance computing, interconnection network, optical networking. ZangDawei, born in 1988. PhD. His main research interests include computer architecture and datacenter networks. AnXuejun, born in 1966. PhD, senior engineer. Senior member of CCF. His main research interests include computer architecture, high performance interconnectio (axj@ncic.ac.cn).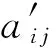
A′(vi,mq)+a(mq,vj).2.3 异常检测


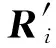
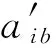
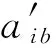
3 路由异常检测实验验证
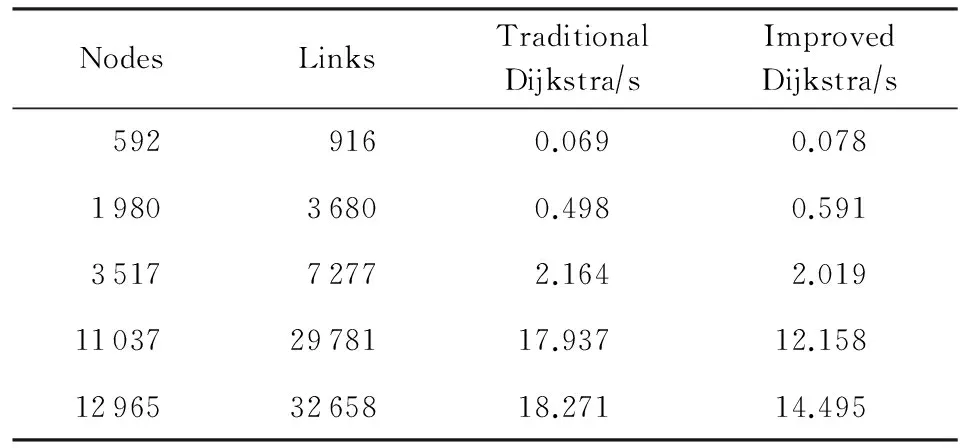
3.1 改进Dijkstra与传统Dijkstra算法比较
3.2 数据中心环境
3.3 数据中心路由变化

3.4 异常检测和异常定位



4 结 论





