网络功能虚拟化环境下安全服务链故障的备份恢复机制
黄 睿 张红旗 常德显
(解放军信息工程大学 郑州 450001) (河南省信息安全重点实验室 郑州 450001) (xjhr1009@163.com)
随着多样化网络业务的迅猛发展,传统网络安全服务模式在动态性、灵活性、可扩展性等方面的弊端愈发突显[1].具体表现为[2]:1)安全功能实现方式的耦合性.现有安全功能,如防火墙、IDS等大都基于硬件中间盒子实现,其在功能上具有专属私有性,建设所需成本较高、可扩展性差、灵活性不足、运用中难以统一管理.2)安全功能部署位置的静态性.现有安全功能大都以静态方式部署在网络的关键位置,拓扑依赖严重,这种僵化的部署方式使其难以根据业务请求的服务构成进行重复使用或者动态重构.为此,探索新型网络安全服务模式成为当下研究的热点[3].
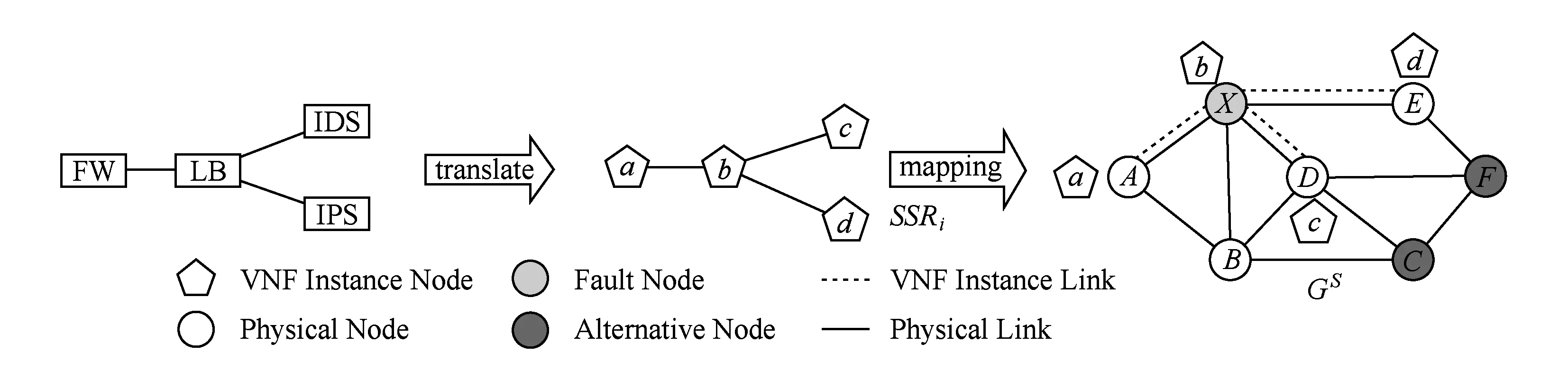
当前,软件定义网络[4](software defined networking, SDN)的发展和网络功能虚拟化[5](network function virtualization, NFV)技术的兴起为探寻新型网络安全服务模式提供了支撑.SDN通过逻辑平面和物理平面的分离,将控制功能从传统的分布式网络设备迁移到集中化的控制平台,进而实现网络的集中管控和开放可编程.NFV将以专有硬件形式部署的网络功能转变为在通用服务器上运行的虚拟网络功能(virtual network function, VNF),将传统网络设备的软件功能和硬件载体解耦开来,减少了在网络特定位置部署专用中间盒子的开销,增加了网络设备部署的灵活性.二者结合,使得网络架构和网络设备更加敏捷[6].由此,借助SDNNFV的安全服务链(security service chain, SSC)技术[7]应运而生.SSC在利用NFV技术将传统安全服务功能虚拟化并部署在通用服务器(也称服务节点)的基础上,借助SDN的流量集中管控功能,根据用户或业务的安全请求引导流量按序经过服务节点上的安全功能实例(也称VNF实例),从而为用户或业务提供可配置的安全服务.
目前,SSC的研究尚处于起步阶段.文献[8]提出一种FRESCO架构,通过安全模块组合的方式生成安全服务,但仅进行了功能上的验证而并未给出具体的实现方案.为此,文献[7]基于SDNNFV提出一种SSC的理论架构,但囿于网络资源的限制,未对逻辑安全服务请求如何向具体的、优化的VNF实例和VNF路径映射做出说明.虽然文献[9]在文献[7]的基础上进一步将SSC映射问题抽象为整数线性规划(integer linear programming, ILP)问题,根据物理节点的服务能力和物理链路的容量约束选择可映射的VNF实例和VNF路径并设计高效的启发式算法求解此问题,但未考虑到SSC模式下可能面临的故障性问题.实际网络中,受自然或人为因素影响,承载安全服务功能的物理网络资源(物理节点物理链路)可能发生故障或性能劣化[10],这将影响SSC的可靠性,严重时还可能导致无法对后续安全服务请求做出及时有效的响应.因此,SDNNFV下SSC故障的备份恢复问题亟待解决.SSC故障的备份恢复旨在,当承载VNF实例VNF链路的服务节点物理链路发生故障时,采用一定方法及时有效地完成VNF实例的更替和流量路由路径的切换,以最小化故障对用户业务带来的影响.
为此,本文提出一种SSC故障的备份恢复机制以应对SSC模式下难以避免的故障性问题.该机制能够有效提高SSC在发生物理节点或物理链路故障时的故障修复率,在用户业务容忍时间内保证服务的连续性.本文贡献主要包含3个方面:
2) 针对节点故障重映射问题,提出改进的离散粒子群(discrete particle swarm optimization, DPSO)算法求解该多目标优化问题(multi-objective opti-mizing problem, MOP),在最大化成功恢复安全服务请求数目的同时最小化VNF实例和VNF路径占用其重映射目标上备用资源的比例.
3) 针对链路故障重定向问题,设计动态路径分割算法求解该混合整数规划(mixed integer progra-mming, MIP)问题,最大化底层物理网络资源剩余价值.
1 相关工作
1) SSC优化构建.首先,需要依据用户或业务的安全请求,在满足网络资源约束的条件下,确定VNF实例的部署数量、位置,并规划流量路由路径,达到最小化安全服务时延等优化目标.现有研究大都从资源约束角度出发,提出满足约束条件的SSC优化构建策略.Dwaraki等人[14]将网络拓扑转换为分层图,采用Dijkstra算法逐层选择网络功能实例和路由路径,但未考虑对大规模物理网络而言,分层图可能带来的存储开销.Xiong等人[15]采用两阶段映射方案,分别基于网络功能的服务能力和网络链路的容量约束选择可映射的服务节点和路由路径,但可能因为服务节点间距离过大而影响服务时延.为适应更大规模的网络基础设施,Luizelli等人[16]将SSC优化构建问题抽象为ILP问题,并设计启发式算法高效求解此问题.
2) SSC执行调度.构建阶段完成后,需考虑到SSC的执行调度问题,即当网络中存在多条SSC时,需要优化服务节点中提供某一特定功能的虚拟节点上多个VNF实例请求的执行顺序,根据需要对VNF实例进行实时调度,以实现最小化安全服务请求的平均等待时间等目标.Riera等人[17]首次提出服务节点上VNF实例的执行调度问题,并对其进行了形式化的定义.文献[18]在文献[17]基础上,将最小化完成时间作为可行方案的优化目标,但并未给出具体的解决方案.Mijumbi等人[19]在解决了VNF实例资源分配问题的基础上,基于禁忌搜索算法解决VNF实例的执行调度问题.
3) SSC故障的备份恢复.SSC优化构建和SSC执行调度问题侧重于SSC正常运行时的问题讨论,而涉及到可靠性保证的SSC故障的备份恢复问题也不容忽视.作为本文研究的重点,SSC故障的备份恢复问题是指,当承载VNF实例VNF链路的服务节点物理链路出现故障时,需要在不影响SSC初始构建资源的条件下,采用预留备用资源重建VNF实例和VNF链路,及时完成VNF实例的更替和流量路由路径的切换,以保证安全服务的可靠性和连续性.在此问题中,物理平面的正常运行是为用户提供安全服务的根本保障.然而,在可控或不可控因素影响下,物理网络资源(物理节点物理链路)都可能发生一定程度的故障.鉴于SDNNFV下资源共享的特性,任何单一物理资源故障都会影响使用该资源的多条SSC,进而影响为用户提供的安全服务.因此,除了为SSC提供有效的优化构建和执行调度方案外,保证SSC故障发生时的生存性也至关重要.
为了增强SSC的生存抗毁性,Nguyen等人[20]提出了一种服务功能链的故障转移机制,通过在线替换故障VNF实例并动态迁移受故障影响流量以减少故障恢复时延,但并未考虑替换VNF实例和迁移流量路径对新到达SSC构建请求的资源制约.Suh等人[21]提出的分布式故障恢复机制,在不介入控制平面的条件下利用寄存在每一个服务节点中的故障恢复代理快速检测和恢复受影响的VNF实例,从而进行即时地故障恢复,但未考虑故障恢复代理带来的额外资源开销和性能损耗.Lee等人[22]提出了一种服务链的故障自恢复方案,通过数据平面的信令方式将受故障影响的服务节点自动地转移到其他正常节点上,但未考虑转移对象可能存在的潜在性故障可能.综上,现有研究成果较少且着重关注于故障发生时受影响VNF实例的即时故障恢复和流量路由路径变换,并未综合考虑其可能带来的资源约束、时延损耗和故障转移目标的可靠性.此外,现有成果未对故障发生对象(节点链路)的类型进行分类讨论,对SSC中的故障问题一概而论,具有一定的局限性.
通过梳理现有相关工作不难发现,针对SSC故障的备份恢复问题,目前尚没有一种机制能够在既保证服务可靠性又不制约接受新请求资源的基础上,为SSC中2类故障问题提供高效的备份恢复解决方案.因此,本文借助SDNNFV架构,提出一种SSC故障的备份恢复机制,综合考虑节点故障重映射和链路故障重定向2个方面,为SSC的进一步推广应用提供支撑.
2 问题概述
2.1 物理平面和安全服务请求
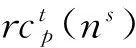

Fig. 1 The mapping topology of SSC图1 SSC映射拓扑图
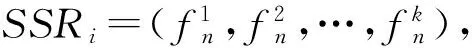
2.2 安全服务链故障
SSC故障一般分为物理节点故障和物理链路故障.实际网络中,一个物理节点发生故障通常会导致一个区域的物理节点在相对集中的时间内发生故障,即发生多节点故障.因此,将SSC中物理节点故障按时间顺序建模为一系列单节点故障集合PNF={pnf1,pnf2,…},对于某单节点故障pnf1,用ts(pnfi)和te(pnfi)分别定义故障发生和结束的时刻,且ts(pnfi) 同样地,将SSC中物理链路故障建模为PLF={plf1,plf2,…}.由于Gill等人[10]在分析链路故障相关性时发现,超过50%的链路故障是由单链路故障引起的,并且超过90%的链路故障涉及不超过5条链路.因此,本文侧重考虑物理链路故障中最常见的单链路故障问题.即在某时刻t,∀i,j,物理链路故障plfi和plfj不同时发生. 节点故障重映射(node failure remapping, NFRM)是指,在发生物理节点故障后,依据当前物理平面状态,及时地为受影响的VNF实例节点和其关联的VNF实例链路重新分配资源,使SSC恢复正常工作. 如图2所示,当GS中的物理节点X发生故障时,SSRi中需要重映射的部分包含VNF实例节点b以及与之相连的VNF实例链路(b,a),(b,c)和(b,d).因此,LR(b)={(b,a),(b,c),(b,d)},NR(b)={a,c,d},NS(b)={A,D,E}. Fig. 2 The instance of single-point fault图2 单节点故障实例 对于NFRM问题,可抽象为以Max{Obj1,Obj2}(3.2.1节中详细描述)为目标,满足以下映射条件的优化问题: (1) (2) 链路故障重定向(link failure redirect, LFRD)是指,在发生物理链路故障时,动态调整底层物理路径流量分割比例,将受影响流量从故障物理链路迁移到正常物理链路当中,从而避免重映射方法带来的服务中断时间较长的影响,使得SSC在最短时间内恢复正常工作. 如图3所示,当GS中的物理链路l(B,E)发生故障时,映射在之上的VNF实例链路l(a,c)需要重定向. Fig. 3 The instance of single-link fault图3 单链路故障实例 对于LFRD方法,可以抽象为以Max{S(GS)}为目标(3.3.1节中详细描述),满足以下映射条件的优化问题: fredirect:li→l′(A,,B),l′(A,,B)∈Path(A,B), (3) 其中fredirect表示VNF实例链路重定向;Path(A,B)表示物理节点A,B间物理链路穷举集合;l′(A,,B)表示集合中的某一条可用物理链路,即把VNF实例链路上的流量重定向到正常的物理链路上,以完成SSC物理链路故障恢复. 本文提出的NFV环境下SSC故障的备份恢复机制包含3个阶段:1)物理平面初始化阶段,即为每个物理资源(节点、链路)都按比例预留备份资源.对于物理节点,采用图的连通性理论构造可用节点候选集合;对于物理链路,采用路径遍历穷举法构造可用链路候选集合,尽可能多得为受故障影响对象提供重映射重定向目标.2)当有安全服务请求SSR到达时,采用已有的服务功能链构建方法[7,9,10]为其分配物理资源并提供安全服务.3)当发生节点故障时,基于改进的DPSO算法求解NFRM,实现VNF实例节点的即时迁移;当发生链路故障时,基于动态路径分割算法求解LFRD,实现VNF实例链路上流量的动态转移. 物理平面初始化包括物理节点初始化和物理链路初始化2个方面,通过在初始化阶段构建候选集合,有利于减小故障发生时主备用资源间的制约,缩小重映射重定向问题的搜索空间,在提高故障恢复成功率的同时提升算法效率. 1) 物理节点初始化 在物理节点x发生故障后,其承载的VNF实例节点及与这些VNF实例节点相连的VNF实例链路都需要重新映射.文献[23]中指出,一个物理节点故障可能会导致与它相邻区域内的物理节点故障发生率增加.因此,为了保证节点故障重映射方法的成功率,x的候选节点应该在一定范围内保持与故障节点x的不连通性.同时,为了降低地理范围导致的资源开销和传输时延,应限定候选节点与故障节点x间的相对距离. 首先,基于图的连通性理论,构造物理网络GS的邻接矩阵: (4) 抽选出矩阵中故障节点x所对应的行列,判断行列中元素的值,值为1则说明二者连通,为0不连通.选取值为0的节点构成初始候选节点集合 (5) 该集合是由物理网络GS中,初始候选节点集合IBN和故障节点x之间相对距离小于阈值D的节点元素构成的集合,也是初始化阶段构造的最终物理节点候选集合. 图2实例中,给定D=2,则初始候选节点集合为LBN(GS,x)={X,F,C},最终候选节点集合为BN(GS,x,2)={F,C}. 2) 物理链路初始化 当物理链路l(A,B)发生故障时,需要对其所承载的VNF实例链路li进行重定向.此处,采用路径遍历穷举法构造候选链路集合BL,集合中的元素需在保证VNF实例节点映射状态不变的条件下,限定物理节点间跳数不超过阈值J. 首先,遍历计算端节点A,B间的通路,构造可达路径集合RLA,B={l(node1),l(node2),…}. 然后,计算可达路径集合RLA,B中候选路径节点nodei的个数count(nodei),定义候选路径集合BL如下: BL(GS,l(A,B),J)= (6) 该集合是物理网络GS的可达路径集合RLA,B中,物理节点间跳数不超过阈值J且与原映射路径不重叠的元素构成的集合,即初始化阶段构造的物理链路候选集合. 图3实例中,设定J=3,可达路径集合为RLB,E={l(B,E),l(B,C,D,E),l(B,A,D,E),l(B,A,F,E)},候选链路集合为BL(GS,L(B,E),3)={l(B,A,D,E),l(B,A,F,E)}. 3.2.1 节点故障重映射的多目标优化模型 物理平面节点故障问题可分为单节点故障和多节点故障问题,由于物理节点故障的发生具有一定的随机性,无法预知未来可能发生故障的节点[24].因此,在节点故障重映射问题中,无法同时解决多节点故障问题,只能将其划分为单节点故障问题逐一优化.NFRM旨在最大化成功恢复安全服务请求数目的同时最小化VNF实例节点和VNF实例链路占用其重映射目标上备用资源的比例,而成功恢复数目的提高势必会带来资源消耗的增多,这2个目标函数相互冲突,不存在唯一的全局最优解使得二者都达到最优.但是,存在一些解使得某个目标函数较优,同时其他目标函数不至于劣化,这样的解称为非劣有效解,又称Pareto最优解[25].为此,我们基于改进的DPSO算法来求解该MOP.首先,建立NFRM的MOP模型: 1) 变量定义 2) 约束条件 ① 资源容量约束 (7) (8) 式(7)和式(8)分别表示对任意候选节点或物理链路,用于重映射的节点资源容量和链路带宽容量不得超过该节点或链路的实时剩余备用容量. ② 流量守恒约束 (9) (10) ∀j(1≤j≤|LR(ni)|),∀x′∈BN(GS,x,D), ③ 变量取值约束 (11) 3) 目标函数 (12) Obj2= (13) max(Obj1,Obj2). (14) NFRM进行故障节点重映射时,有2方面的优化目标需重点考虑.一方面应尽可能最大化成功恢复安全服务请求的数目(式(12)),以确保用户安全服务不受影响;另一方面应最小化VNF实例节点和VNF实例链路占用其重映射目标上备用资源的比例(式(13)中α,β为权重因子),优先使用剩余备用资源容量大的物理节点和链路,有利于备用物理资源的负载均衡和物理平面整体抗毁能力的提升.式(14)为NFRM方法的Pareto目标函数. 3.2.2 改进的离散粒子群算法 DPSO算法适合于对离散优化问题的解空间进行多点随机性搜索,其具有形式简洁、收敛迅速、参数调节机制灵活等特点,目前已成功应用于MOP的求解当中. DPSO算法中,每个粒子可以看作解空间中的一个点,如果粒子的群体规模为N,则第num=1,2,…,N个粒子可以用速度向量vnum和位置向量xnum表示,种群中的粒子num通过式(15)来更新自己进化过程中的速度和位置: (15) 其中,w≥0代表惯性压缩因子;c1,c2≥0代表加速因子;r1和r2是[0,1]内均匀分布的随机数;xnum是粒子的当前位置;pBest[num]代表第num个粒子的个体最优解;gBest代表整个群体的全局最优解.式(15)中第1条为粒子速度更新公式,其中,第1部分为粒子依据自身速度进行惯性运动,表示粒子对当前自身运动的信任;第2部分为粒子的自我认知部分,表示粒子对自身历史的思考;第3部分为粒子的社会认知部分,表示粒子在群体中的信息共享和相互协作.第2条采用sigmoid函数将粒子速度映射到[0,1]区间,作为下一步取值的概率.第3条为粒子的位置更新公式. DPSO算法的参数中,惯性压缩因子w对粒子的搜索能力有很大的影响,它决定搜索步伐的大小,较大的w有利于全局搜索,较小的w有利于局部搜索.通常在开始时搜索步伐大些,随着迭代次数的增加,减小w值以防止错过最优解.本文所提故障恢复问题具有较高的时效性要求,因此,需要选择一个合适的w值,在平衡全局和局部搜索能力的同时加快算法的收敛速度.式(16)为我们提出的一种惯性压缩因子w的非线性自适应策略,使其值在每一轮迭代过程中动态变化. (16) 本文参考文献[27],提出改进的DPSO算法求解NFRM问题,伪代码如算法1所示: 算法1.节点故障重映射算法. 输入:物理网络拓扑GS、故障物理节点ni; 输出:Pareto最优解. Step1. 初始化,设定种群规模N、当前迭代次数t=0、随机产生每个粒子的初始位置x0、初始速度v0; Step2. 用目标函数Obj1,Obj2分别计算每个粒子的适应度值: Fornum=1 toN Fitness1[num]=Obj1(xnum); Fitness2[num]=Obj2(xnum); End For Step3. 在2个目标函数Obj1和Obj2下分别对每个粒子求得个体极值: Fornum=1 toN pBest[1,num]←Obj1; pBest[2,num]←Obj2; End For Step4. 对2个目标函数Obj1和Obj2,分别求2个全局极值: gBest[1]←Obj1; gBest[2]←Obj2; Step5. 分别计算个体极值的均值和全局极值的均值: pBest[num]=Average(pBest[1,num],pBest[2,num]); gBest=Average(gBest[1],gBest[2]); Step6. 用Step5计算所得的gBest和pBest[num]依据式(15)更新每个粒子的速度vi和位置xi,并依据式(16)更新惯性压缩因子w的值; Step7. 如满足条件,则输出最优解,否则t++,转Step2.结束条件为tmax>t或当前解已稳定. 3.3.1 链路故障重定向的混合整数规划模型 单链路故障问题在物理平面链路故障问题中最为常见,其发生具有瞬时性、不确定性,并且往往会给用户安全服务请求造成较长时间的中断.因此,本文将其建模为MIP问题并提出动态路径分割算法,在发生物理链路故障时,动态调整底层物理路径流量分割比例,重定向受影响流量至正常物理路径.LFRD的目标在于最大化底层物理网络资源剩余价值,使有限物理资源承载尽量多的安全服务请求.首先,进行算法条件准备: 1) 变量定义 2) 约束条件 ① 链路带宽约束 (17) ∀l′(A,,B)∈BL(GS,l(A,B),J), 式(17)表示重定向VNF实例链路li中的φ份流量不能超过其宿主物理链路实时剩余带宽容量. ② 流量守恒约束 (18) ∀l′(A,,B)∈BL(GS,l(A,B),J), 式(18)表示当VNF实例链路li中的φ份流量重定向到物理链路l′(A,,B)上时,物理链路上的净流量应该等于链路请求带宽;否则,应满足流量守恒定律. ③ 负载均衡约束 (19) (20) ④ 变量取值约束 (21) 3) 目标函数 (22) 式(22)表示最大化底层物理资源剩余价值,是求解LFRD方法的目标函数,其中ρ代表链路价值转换权重. 3.3.2 动态路径分割算法 动态路径分割算法是指,在不改变VNF实例节点映射关系的前提下,将安全服务请求中VNF实例链路上的流量按比例分割并重定向在多条可用物理链路上.本文设计动态路径分割算法用于求解LFRD问题的最优解,伪代码如算法2所示: 算法2.链路故障重定向算法. 输入:物理网络拓扑GS、故障物理链路l(A,B)、路径分割率φ=(1+ε)|BL(GS,l(A,B),J)|; 输出:底层物理资源剩余价值S(GS). Step1.判断VNF实例链路li是否具有路径可分割性.如有,依据3.3.1节中算法条件准备2)中约束条件为其建立线性约束并初始化控制变量ε=0;S(GS)=0;否则,退出; Step2.针对VNF实例链路li,按照路径分割比例φ将其分别重定向在l′(A,,B)∉BL(GS,l(A,B),J),并依据式(22)计算当前底层物理资源剩余价值T_S(GS); Step3.比较T_S(GS)和S(GS).若T_S(GS)>S(GS),则S(GS)=T_S(GS); Step4.控制变量ε++; Step5.当ε<|BL(GS,l(A,B),J)|-1时,返回Step2;否则,退出; 实际中,对于安全服务请求中一些特殊的服务功能,路径分割往往会导致其服务的中断或者破坏其服务的连续性.因此,算法Step1阶段,首先判断VNF实例链路li是否可进行路径分割.对于可分割的VNF实例链路,在满足约束条件的情况下,依据“打擂”思想求解底层物理资源剩余价值的最大值;而对于不可分割的VNF实例链路,无法采用本文所提动态路径分割算法求解,只能采用传统方法对故障物理链路及相关节点重新进行资源映射或对物理平面数据包进行标记改造,这超出了本文的研究范围. 本文开展仿真实验的目的有3个方面: 1) 在不同物理网络环境下,评估本文方法的适应性;通过设置不同资源容量载荷的物理网络拓扑,比较本文方法性能差异. 2) 在不同故障模型下,评估本文方法的有效性;由于传统服务链映射方法暂未考虑物理网络故障问题,Lee等人也仅在文献[22]中提出一种服务链的故障自恢复方案,故都不便与本文方法直接进行比较.因此,本文将经典的服务链映射方法[16]和服务链故障自恢复方案[22]分别扩展为未采用故障恢复方法的NFRMLFRD算法(N_NFRMN_LFRD)和采用故障自恢复方法的NFRMLFRD算法(S_NFRMS_LFRD)与本文所提(P_NFRMP_LFRD)方法进行比较. 3) 在不同故障发生频率下,测试资源主用比例λ对本文方法性能的影响;针对不同故障发生率,探索资源主用比例的最佳取值. 仿真实验在配置Intel Core i7-6300HQ @3.40 GHz,8 GB内存的PC机上进行,借助GT-ITM[28]工具生成底层物理网络拓扑并利用Matlab工具对实验结果进行分析.每次实验运行50 000个时间单位. 实验设置3种不同资源容量载荷的物理网络拓扑对本文方法进行评估,拓扑中的每对节点以0.5概率相连,节点类型及个数如表1所示.假设物理网络中的每个服务节点都能提供计算、存储和带宽3种资源,为了便于实验分析,重点关注服务节点的存储资源(限定每个服务节点的最大存储容量为16 GB),而节点间的物理链路,重点关注其带宽资源(限定每条物理链路的最大负载量为2 Gbps).针对在物理网络Phy1中,节点资源总量(单位:M)和链路带宽(单位:Mbps)分别服从[0,50]和[50,100]的均匀分布.物理网络Phy2中,节点资源总量和链路带宽分别服从[50,100]和[100,200]的均匀分布.物理网络Phy3中,节点资源总量和链路带宽分别服从[0,200]和[0,400]的均匀分布.物理节点故障的到达服从时间单位为100、强度为pn的泊松过程,故障持续时间服从均值为dn个时间单位的指数分布,物理节点候选集合相对距离D=3;物理链路故障的到达服从时间单位为100、强度为pl的泊松过程,故障持续时间服从均值为dl个时间单位的指数分布,物理链路候选集合跳数J=4. Table 1 Number of Nodes in the Experimental Topology表1 实验拓扑节点个数信息 假设网络中有6种安全功能,每种安全功能有3种VNF实例.安全服务请求SSR中VNF实例节点的数目服从[3,5]的均匀分布,VNF实例节点间以0.5的概率相连.VNF实例节点资源需求和VNF实例链路带宽需求分别服从[1,10]和[1,15]的均匀分布.安全服务请求SSR的到达服从时间单位为100、强度为4的泊松过程,请求的生命周期服从均值为40个时间单位的指数分布. 对于3.2节提出的基于改进的DPSO算法求解NFRM,将目标函数中节点资源权重α和链路资源权重β都设为1.DPSO算法中,设种群规模N=100,最大迭代次数tmax=50,初始权重winitial=1,最终权重wfinal=0.1,加速因子c1,c2均取2;对于3.3节提出的基于动态路径分割算法求解LFRD,设链路价值转换权重ρ=1. 安全服务请求故障修复率是指使用故障恢复方法后,能够正常运行的安全服务请求数目与故障发生前正常运行的安全服务请求数目的比值,反映了故障修复算法的有效性.本文通过模拟物理节点故障和物理链路故障,从安全服务请求故障修复率角度对3.2和3.3节所提方法进行验证,仿真结果如图4~11所示. 图4和图5展现了在3种不同资源容量载荷的物理网络上,NFRM和LFRD方法的故障修复率和故障修复时间.为便于比较,物理节点故障强度pn和物理链路故障强度pl均取3,故障持续时间dn和dl均取25,主用比例λ均取75%. Fig. 4 The fault-recovery rate of NFRMLFRD in different substrate networks图4 不同物理网络下NFRMLFRD的故障修复率 Fig. 5 The fault-recovery time of NFRMLFRD in different substrate networks图5 不同物理网络下NFRMLFRD的故障修复时间 由图4(a)可知,NFRM方法在3种不同资源容量载荷的物理网络上,故障修复率较为接近.其中,物理网络Phy1和Phy3下故障修复率分别为92%和86%;而在物理网络Phy2下,安全服务请求故障修复率大概在96%,高于其他2种类型物理网络,这主要是因为Phy2提供的节点资源总量和链路带宽分别服从[50,100]和[100,200]的均匀分布,而VNF实例节点资源需求和VNF实例链路带宽需求分别服从[1,10]和[1,15]的均匀分布,从资源配置角度来看,Phy2能够在满足请求资源的同时保证较高的故障修复率.观察图4(b)可知,LFRD方法在3种物理网络上的故障修复率相差不大,但相比图4(a)而言,物理网络Phy1和Phy3下的故障修复率分别提高了1%和2%,可见LFRD方法即使在资源配置不合理的物理网络环境下,仍能保证较高的故障修复率,对于多样化物理网络配置具有更好的适应性. 图5(a)表示NFRM方法在3种不同资源容量载荷的物理网络上的故障修复时间.可以看出,随着SSC个数的增多,不同物理网络下的NFRM故障修复时间不断增长.这是因为随着SSC个数的增多,可能发生故障的物理节点链路比例也随之增大.其中,物理网络Phy1和Phy3下故障修复时间波动性较大;而在物理网络Phy2下,故障修复时间均匀增大并趋向于稳定,这主要是因为Phy2提供的节点资源总量和链路带宽总量能更好地满足物理网络资源配置需求.观察图5(b)可知,LFRD方法在3种物理网络上的故障修复时间较为接近,但相比图5(a)而言,在资源配置不尽合理的物理网络环境下,Phy1和Phy3下的故障修复时间分别延长了0.9 s和0.5 s,即使在资源配置较为合理的Phy2下,仍存在近1s的延迟,可见对于未采用启发式算法求解的LFRD方法,虽然能够保证较高的故障修复率,但是当SSC个数增多时,存在故障修复时间较长的弊端. Fig. 6 The fault-recovery rate of different NFRMs when dn=25图6 dn=25时各NFRM的故障修复率 Fig. 7 The fault-recovery rate of different NFRMs when dn=50图7 dn=50下各NFRM的故障修复率 Fig. 8 The fault-recovery rate of different LFRDs when dl=25图8 dl=25下各LFRD的故障修复率 Fig. 9 The fault-recovery rate of different LFRDs when dl=50图9 dl=50下各LFRD故障修复率 如图6所示,当dn一定时,P_NFRM的平均故障修复率可达95%,分别高出S_NFRM和N_NFRM五个百分点和十个百分点.对比图7还可看出,当dn增加时,P_NFRM性能受影响不大,而其他2种方法性能明显下降.由此可见,当发生多节点故障概率增加时,本文方法具有更好的稳定性,这是因为本文方法对可能发生的故障问题进行了前摄性的准备.此外,当dn较大时,S_NFRM和N_NFRM的曲线较为接近,主要是因为当节点故障概率增加时,2种方法恢复故障链的效率明显降低.观察图8可知,当dl较小时,P_LFRD的平均故障修复率远高于其他2种方法且性能发挥较为稳定.对比图9可以看出,当dl较大时,P_LFRD的曲线波动较为明显,呈现出一定的不稳定性,这是因为随着链路故障持续时间的增长,物理网络中发生区域性链路故障的概率增加,为链路故障修复带来了一定的困难. 资源主用比例λ的取值直接影响本文方法的有效性,增大λ的取值,一方面可以提高SSC构建的成功率;另一方面却会减少故障备份的可用资源,为SSC的故障恢复增加难度.因此,本文通过仿真实验探索不同故障发生频率下最优的λ取值.实验在物理网络Phy2上进行,故障持续时间dn和dl均取25. 由图10(a)可知,NFRM在pn取1,2,3,4时的最优节点资源主用比例分别为80%,70%,67%和60%,可见,λ的取值与故障发生强度pn呈现出一定的线性相关性,在故障强度增大时,主用比例逐渐减小,并且减小的趋势逐渐平缓.观察图10(b)具有类似的曲线特性.可见,曲线结果与前述分析具有一致性. Fig. 10 The impact of different link resourcemain-proportion on NFRMLFRD图10 不同链路资源主用比例对NFRMLFRD的影响 本文主要围绕NFV环境下SSC故障恢复问题展开讨论,在已有无故障恢复服务链构建方法基础之上,创新性地提出了一种SSC故障的备份恢复机制.针对物理节点故障和物理链路故障2种不同的情形,通过预留备用资源和构造初始化候选集合来提高故障发生时SSC的恢复能力,分别设计改进的DPSO算法和动态路径分割算法求解此问题.实验表明,本文方法可在不同物理网络环境下和不同故障模型下有效提高安全服务请求的故障修复率,增强SSC的生存抗毁性. 未来工作主要从以下3个方面展开:1)求解MIP的动态路径分割算法只适用于中小规模物理网络,当面临大规模物理网络时,为保证故障恢复的时效性,应设计高效的启发式算法近似求解;2)收集SSC故障历史数据并进行统计分析,设计更具有针对性的故障恢复方案;3)进一步试验探索主用比例对本文方法的影响,形式化定义并寻求最优解. [1]Paul S, Pan J L, Jain R. Architectures for the future networks and next generation Internet: A survey[J]. Computer Communications, 2011, 34(1): 2-42 [2]Quinn P, Guichard J, Yadav N. Network Service Chaining Problem Statement, RFC 7498[S]. Fremont, CA: IETF, 2015 [3]Huang Tao, Liu Jiang, Huo Ru, et al. Survey of research on future network architectures[J]. Journal on Communications, 2014, 35(8): 184-197 (in Chinese)(黄韬, 刘江, 霍如, 等. 未来网络体系架构研究综述[J]. 通信学报, 2014, 35(8): 184-197) [4]Lantz B, Heller B, Mckeown N. A network in a laptop: Rapid prototyping for software-defined networks[C]Proc of the 9th ACM SIGCOMM Workshop on Hot Topics. New York: ACM, 2010: 1-6 [5]Chiosi M, Clarke D, Willis P, et al. Network functions virtualization-introductory white paper[OL]. [2017-06-22]. https:portal.etsi.orgnfvnfv whitepaper.pdf [6]Jeff W. Delivering Security Virtually Everywhere with SDN and NFV: IHS INFONETICS White Paper[OL]. [2017-04-28]. http:www.juniper.netassetsfrfrlocalpdfanalyst-reports2000602-en.pdf [7]Lee W, Choi Y H, Kim N. Study on virtual service chain for secure software-defined networking[OL]. [2017-11-12]. http:onlinepresent.orgproceedingsvol29_201336.pdf [8]Shin S, Porras P, Yegneswaran V, et al. FRESCO: Modular composable security services for software-defined networks[C]Proc of the 20th Annual Network and Distributed System Security Symp. San Diego: Internet Society, 2013: 32-48 [9]Ocampo A F, Gil-Herrera J, Isolani P H, et al. Optimal service function chain composition in network functions virtualization[C]Proc of the 11th Int Conf on Autonomous Infrastructure, Management and Security. Berlin: Springer, 2017: 62-76 [10]Gill P, Jain N, Nagappan N. Understanding network failures in data centers: Measurement, analysis, and implications[J]. ACM SIGCOMM Computer Communication Review, 2011, 41(4): 350-361 [11]Hwang J, Ramakrishnan K K, Wood T. NetVM: High performance and flexible networking using virtualization on commodity platforms[J]. IEEE Trans on Network and Service Management, 2015, 12(1): 34-47 [12]Martins J, Ahmed M, Raiciu C, et al. Enabling fast, dynamic network processing with clickOS[C]Proc of the 2nd ACM SIGCOMM Workshop on Hot Topics in Software Defined Networking. New York: ACM, 2013: 67-72 [13]Zhang Wei, Liu Guyue, Zhang Wenhui, et al. OpenNetVM: A platform for high performance network service chains[C]Proc of the 2016 Workshop on Hot Topics in Middleboxes and Network Function Virtualization. New York: ACM, 2016: 26-31 [14]Dwaraki A, Wolf T. Adaptive service-chain routing for virtual network functions in software-defined networks[C]Proc of the 2016 Workshop on Hot Topics in Middleboxes and Network Function Virtualization. New York: ACM, 2016: 32-37 [15]Xiong Gang, Hu Yuxiang, Lan Julong, et al. A mechanism for configurable network service chaining and its implementation[J]. KSII Trans on Internet & Information Systems, 2016, 10(8): 3701-3727 [16]Luizelli M C, Bays L R, Buriol L S, et al. Piecing together the NFV provisioning puzzle: Efficient placement and chaining of virtual network functions[C]Proc of the 12th Int Symp on Integrated Network Management. Piscataway, NJ: IEEE, 2015: 98-106 [17]Riera J F, Hesselbach X, Escalona E, et al. On the complex scheduling formulation of virtual network functions over optical networks[C]Proc of Int Conf on Transparent Optical Networks. Piscataway, NJ: IEEE, 2014: 1-5 [18]Jordi F R, Eduard E, Josep B, et al. Virtual network function scheduling: Concept and challenges[C]Proc of the 2nd Int Conf on Smart Communications in Network Technologies. Piscataway, NJ: IEEE, 2014: 1-5 [19]Mijumbi R, Serrat J, Gorricho J L, et al. Design and evaluation of algorithms for mapping and scheduling of virtual network functions[C]Proc of the 2015 Int Conf on Network Softwarization. Piscataway, NJ: IEEE, 2015: 1-9 [20]Nguyen V C, Kim Y H. A failover mechanism for service function chain[C]Proc of the 2017 Symp of the Korean Institute of Communications and Information Sciences. Seoul, Korean: SoongSil University Press, 2017: 1145-1146 [21]Suh D, Baek H, Jang S, et al. Distributed service function failover mechanism in service function chaining[C]Proc of the 2017 Int Conf on Information Networking. Piscataway, NJ: IEEE, 2017: 148-150 [22]Lee S I, Shin M K. A self-recovery scheme for service function chaining[C]Proc of the 2015 Int Conf on Information and Communication Technology Convergence. Piscataway, NJ: IEEE, 2015: 108-112 [23]Sato Y. IECJIS standard-functional safety of electricalelectronicprogrammable electronic safety-related systems[C]Proc of the 1999 General Conf on Electronics, Information and Communication Engineers. London: Oxford University Press, 1999: 567-568 [24]Xiao Ailing, Wang Ying, Meng Luoming, et al. Virtual network embedding approach to survive multiple node failures[J]. Journal on Communications, 2015, 36(4): 81-88 (in Chinese)(肖蔼玲, 王颖, 孟洛明, 等. 面向多节点故障的生存性虚拟网络映射方法[J]. 通信学报, 2015, 36(4): 81-88) [25]Zheng Jinhua, Jiang Hao, Kuang Da, et al. An approach of constructing multi-objective Pareto optimal solutions using arena’s principle[J]. Journal of Software, 2007, 18(6): 1287-1297 (in Chinese)(郑金华, 蒋浩, 邝达, 等. 用擂台赛法则构造多目标Pareto最优解集的方法[J]. 软件学报, 2007, 18(6): 1287-1297) [26]Zhang Changsheng, Sun Jigui, OuYang Dantong. A self-adaptive discrete particle swarm optimization algorithm[J]. Acta Electronica Sinica, 2009, 37(2): 299-304 (in Chinese)(张长胜, 孙吉贵, 欧阳丹彤. 一种自适应离散粒子群算法及其应用研究[J]. 电子学报, 2009, 37(2): 299-304) [27]Hu Wang, Yen G G, Zhang Xin. Multi-objective particle swarm optimization based on Pareto entropy[J]. Journal of Software, 2014, 25(5): 1025-1050 (in Chinese)(胡旺, Yen G G, 张鑫. 基于Pareto熵的多目标粒子群优化算法[J]. 软件学报, 2014, 25(5): 1025-1050) [28]Calvert K L, Doar M B, Zegura E W. Modeling Internet topology[J]. IEEE Communications Magazine, 1997, 35(6): 160-163 HuangRui, born in 1993. Master candidate. Her main research interests include software defined network and network function virtualization. ZhangHongqi, born in 1962. PhD, professor. His main research interests include network security and classification protection (zhq37922@126.com). ChangDexian, born in 1977. PhD, associate professor. His main research interests include SDN security and trusted computing (changdexian@126.com).2.3 节点故障重映射
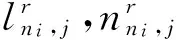
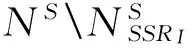
2.4 链路故障重定向


l(A,B)≠l′(A,,B),3 方法描述
3.1 物理平面初始化

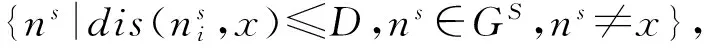
{l(nodei)|count(nodei)-1≤J,
l(nodei)∈ES∉ER,l(nodei)≠l(A,B)},3.2 基于改进的离散粒子群算法求解NFRM
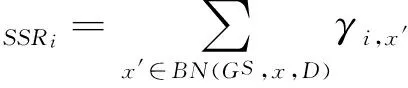

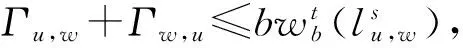


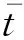
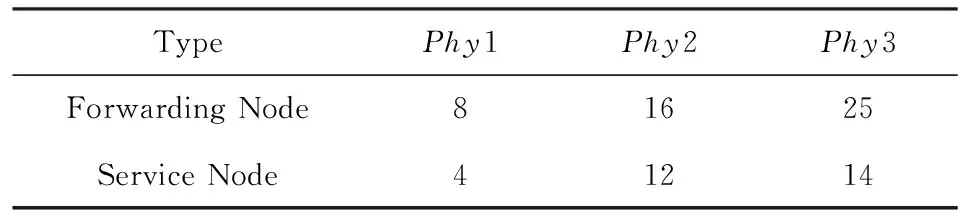
3.3 基于动态路径分割算法求解LFRD


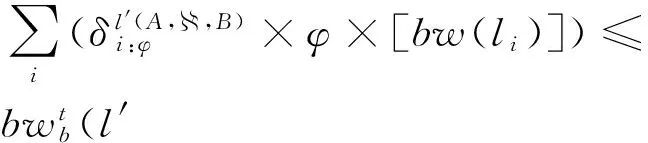

4 仿真实验
4.1 实验设定
4.2 算法适应性


4.3 算法有效性




4.4 主用比例取值探索
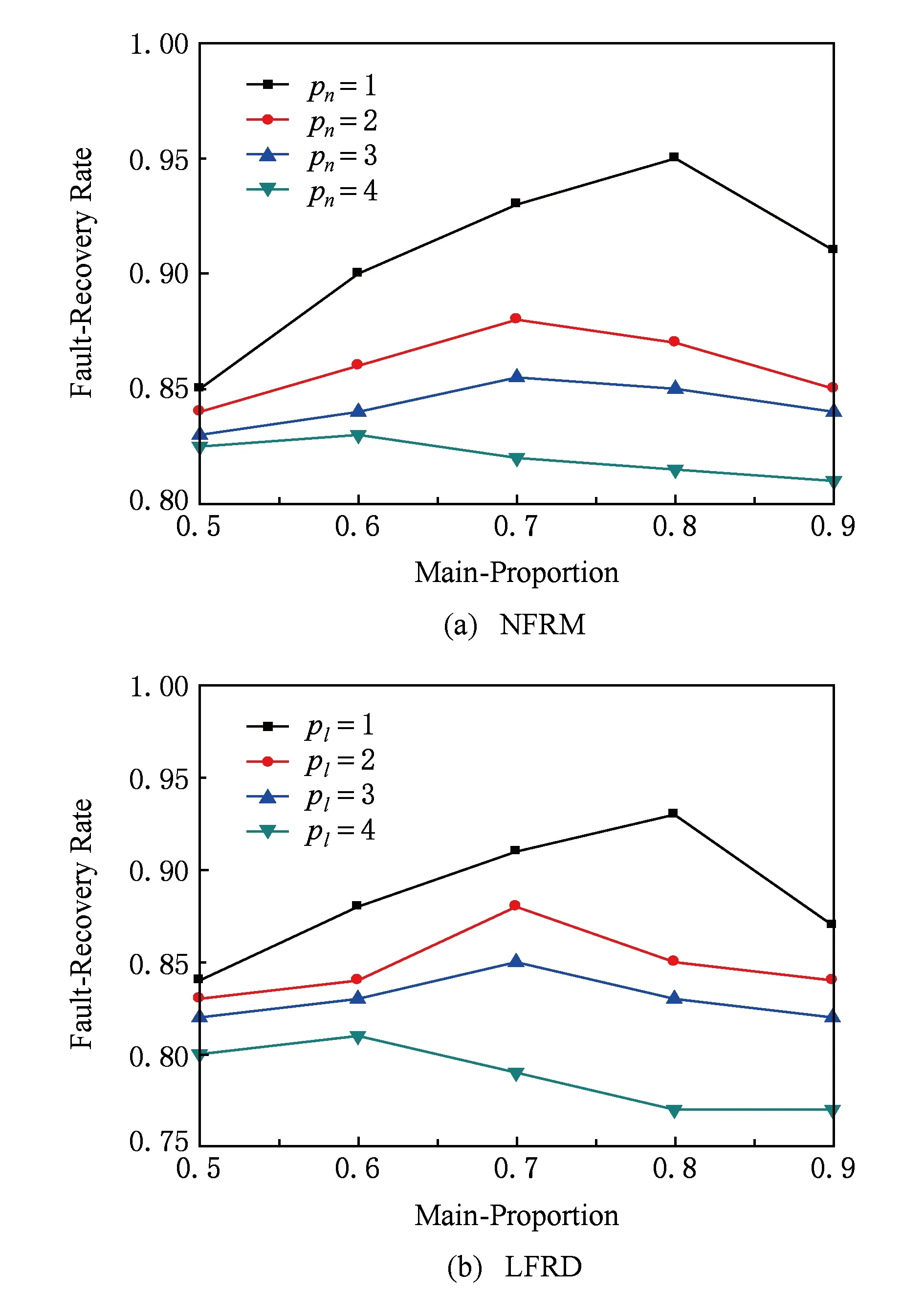
5 结束语




