BDS/GPS 组合导航系统选星算法研究

于寒，秦武

（中国人民解放军92941部队91分队，辽宁葫芦岛市 125000）

0 引言

我国自主研制的北斗卫星导航系统（BDS）由于尚未组网完成，且可见星受应用环境影响较大，在可见星数目较少的情况下，定位解算结果难以满足精度要求，甚至无法完成定位。将BDS和GPS导航卫星组合应用组网，既可以使我制导武器避免因战时美国关闭GPS或敌国对GPS实施干扰造成的限制，又可以在 BDS组网完成前增加可见星数目，改善卫星空间分布特性，从而提升导航系统的定位精度和稳定性。随着北斗卫星导航系统建设的日益完善，以 BDS/GPS双系统组合导航方式已逐渐被靶场试验所采用。

由于 BDS/GPS组合导航系统在同历元时刻可见星数目约为 15颗左右，若继续采用常用的最佳选星法进行选星，需遍历每一个卫星组合，定位解算的运算量将成倍增长，不仅增加了接收机的设计难度，也严重影响了的导航定位的实时性[1]。因此，如何在满足定位精度的前提下，减少参与定位解算的卫星数量，降低运算量，是极为重要的研究课题。

1 BDS/GPS组合导航系统定位精度的关键影响因子

1.1 几何精度因子GDOP

在卫星导航系统中，定位精度是判断卫星定位效果好坏的最主要标准[2]，而GDOP值表征了定位精度的大小，反映了用户接收机与可见星的空间几何分布情况，即：

式（1）中，σ为定位精度标准偏差，USER σ为用户伪距测量误差标准偏差。由式（1）可知，在值一定时，GDOP值越小，定位精度越高。

1.2 卫星分布对GDOP的影响

由文献3推导结果可知：

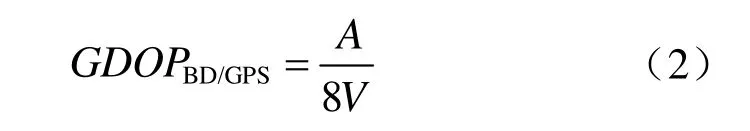
2 BDS/GPS组合导航系统选星算法

2.1 选星数量的确定

由文献4检测结果可知，当测量站选星数目较小时，GDOP下降较快，当选星数目过多时，导航运算量大幅增加，而GDOP变化缓慢。文献5指出，当卫星数量大于6时，GDOP递减幅度很小。

BDS/GPS双系统组网需要至少5颗卫星参与定位解算，且每个系统的卫星数量不少于2颗；而载波相位差分还需要1颗卫星进行误差校验。

综合以上因素，BDS/GPS组合导航系统选星数量确定为6颗。

2.2 可用星的选择

在导航系统取得第一个定位结果后，根据卫星星历可获得各个卫星的仰角信息。为降低多径效应对信号的干扰，需将仰角过低的可见星屏蔽，屏蔽阈值通常设为10°。

卫星信号的信噪比越小，接收机中对应的跟踪环路误差就越大，如果信噪比过小的卫星参与定位解算，必将影响定位结果的准确性。本文将卫星信号的信噪比门限值设为7dB，即小于此值的便作为弱信号卫星予以屏蔽。

文献6仿真结果表明，顶座星（卫星中高度角较大的）的高度角越大，GDOP值越小；底座星（卫星中高度角较小的）的高度角越小，GDOP值也越小；当高度角确定时，底座星方位角差值在80°～120°时，GDOP效果最好，而且方位角差值越均匀，GDOP值越小。大量文献统计结果也与上述仿真结果相一致。基于这一规律，本文借鉴综合模糊评判法思想，采用模糊选星法对参与定位解算的卫星进行选择。

2.3 模糊选星法

模糊选星算法的基本思想就是：在仰角大于10°，信噪比大于7dB的可见星中，选择仰角最大的两颗分别作为第一颗可用星和第二颗可用星，仰角最小的作为第三颗可用星。设仰角最小的第三颗可用星方位角和俯仰角分别为α和e，其余未选择的可见星方位角和俯仰角分别为iα和ei，。将α分别增加90°、180°、270°，在这三个方位角附近的仰角与e最接近的三颗星依次就是要选择的第四、第五、第六颗可用星。模糊选星算法就是在综合考虑方位角和俯仰角两个因素的影响下，运用模糊数学中的模糊综合评判法对第四、第五、第六颗可用星的选取进行最优组合。具体评判方法如下[7-8]：

步骤一：建立因素集。定义α+90°与iα的夹角为iA，e与ei的夹角为iA，则可构成两个模糊向量：利用这两个模糊向量即可构造表示两个因素间模糊关系的矩阵：

步骤三：完成模糊变换。令模糊变换矩阵F=P⋅Z，则F中元素最小值对应的卫星就是第四颗可用星。同理，将α+90°分别替换为α+180°和α+270°，便可在剩余可见星中依次挑选出第五、第六颗可用星。

由此可见，模糊选星算法只需进行一次简单的向量乘法运算，避免了常用的最佳选星法中大量的矩阵求逆和矩阵乘法，极大地提高了运算效率，定位的实时性大为提高。

3 实验及结果分析

下面利用靶场外测接收机来验证算法的正确性。将接收机架设在外场，定位模式设为BDS+GPS模式，仰角屏蔽值设为 10°，信噪比门限值设为7dB，待其差分锁定后记录某一时刻的BDS/GPS原始数据见表1。

表1 BDS/GPS原始数据

采用上文给出的选星算法，选取仰角最大的B6号卫星作为第1颗可用星，选取仰角第二大的G13号卫星作为第2颗可用星，选取仰角最小的G7号卫星作为第3颗可用星，即e=14，α=44。将α分别增加90°、180°、270°，继续按模糊选星法解算步骤进行可依次得到第4颗可用星为B3号卫星，第5颗可用星为G30号卫星，第6颗可用星为G5号卫星，因此可判断出组合（B6，G13，G7，B3，G30，G5）为最佳卫星组合。

下面采用常用的最佳选星法进行验证。经过复杂的解算过程共得到C613种卫星组合，经对比可以看出组合（B6，G13，G7，B3，G30，G5）的GDOP值和定位误差均为最小，证明了本文提出的模糊选星算法能够选出定位精度最高的最佳卫星组合。

4 结束语

目前，国内外关于改进选星算法的研究有很多[9-14]，但基于模糊数学的模糊选星法以其较小的运算量、快速的搜星速度无疑更适用于靶场试验。

现有文献关于模糊选星算法的研究通常是基于单系统星座或算法描述不够准确、完善，本文对BDS/GPS组合导航系统定位精度的关键影响因子、可用星数量及选择方式进行了分析，并详细阐述了模糊选星算法的解算步骤。实验结果证明，该方法简单易行，定位精度高，实时性好，对靶场试验品的导航定位具有重要参考价值。

参考文献：

[1]阮冬茹, 张莫. 组合定位中选星算法的改进研究[J]. 测控技术, 2015, 34(8): 111-113.

[2]DOONG S H.A closed-form formal for GPS GDOP computation [J]. GPS Solutions, 2008,13(3):183-190.

[3]GPS双模导航定位精度分析及仿真[J]. 现代防御技术,2011, 39(4):35-39.

[4]霍航宇, 张晓林. 组合卫星导航系统的快速选星方法[J].北京航空航天大学学报, 2015, 2:273-282.

[5]丛丽, 谈展中. 提高卫星导航定位精度和实时性的选星算法[J]. 系统工程与电子技术, 2008,30(10):1914-1917.

[6]杨一, 高社生, 阎海峰. 临近空间伪卫星几何布局方案设计[J]. 系统工程与电子技术, 2014,36(3):532-538.

[7]杜栋, 庞庆华, 吴炎. 现代综合评价方法与案例精选[M]. 北京: 清华大学出版社, 2008.

[8]卓宁. 靶场试验BD/GPS测量系统组合选星算法[J]. 太赫兹科学与电子信息学报, 2016,14(3):347-349.

[9]M.R.Mosavi. Applying Genetic Algorithm to Fast and Precise Selection of GPS Satellites[J]. Asian Journal of Applied Sciences 4, 2011(3):229-237.

[10]Miaomiao Wei, Ju Wang. A New Satellite Selection Algorithm for Real-time Application[J]. 2012 International Conference on Systems and Informatics.(ICSAl2012)

[11]张文炳, 刘以安, 薛松,等. 北斗/GPS卫星导航系统选星算法研究[J]. 计算机仿真, 2016,33(5):167-169.

[12]张海江, 卓宁. 靶场BD/GPS联合定位及速度解算方法[J]. 信息技术, 2016,6:167-169.

[13]金玲, 黄智国, 李锐等. 多卫导组合系统的快速选星算法研究[J]. 电子学报, 2009, 37(9): 1931-1936.

[14]Yu X L, Sun Y R, Liu J Y, et a1.Fast algorithm of selecting satellites for multiple satellite integrated navigation system[C]//World Congress on Computer Science and Information Engineering. Piscataway, NJ: IEEE Computer Society, 2009,5:121-125.