基于改进A*算法的无人机动态航迹规划
马立
(中国电子科技集团公司第二十研究所,西安 710068)
0 引言
无人机在未来战场上起着举足轻重的作用,而航路规划则是无人机的重中之重,它不仅保证无人机以合理的路线进行规避并打击从而提高无人机的作战效能,而且防止了无人机在协同条件下的碰撞从而保证无人机的安全性。航路规划是实现无人机自主飞行和任务执行的重要手段。在复杂的战场环境下,随着信息量和规划约束条件的增加,对算法的需求也越来越多样化。目前,对于航路规划的研究还集中在单机算法的研究,比如Voronoi图法[1],遗传算法[2],粒子群算法[3]等,对于单无人机的动态航路规划,研究还不够深入。实际环境中,面对突发威胁,无人机不得不改变原有线路重新规划,所以动态航路规划[4]更接近实际战场。
1 算法的选取
航路规划的算法很多,但每种算法都有各自的优缺点,如何选取算法也显得格外重要。遗传算法[2]不需要确定的模型,算法鲁棒性强,但对复杂的环境和航路不仅难以进行算法编码,而且搜索时间长;蚁群算法[5-6]具有正反馈,分布计算等优点,但算法初始信息素设定和信息素更新规则难以确定。
A*算法[7-9]是人工智能中的一种启发式搜索算法,它将实际代价看成两部分之和,即已经付出的代价和将要付出的代价,该代价函数可表示为式(1):
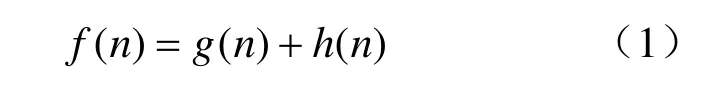
其中,n表示当前节点,g(n)和h(n)表示两个代价函数,本文表示为距离。设Spoint表示起点,Epoint表示目标点,则g(n)表示从Spoint到当前点n的路径代价;h(n)表示从n到Epoint的估计代价,称之为启发函数。f(n)就表示从Spoint出发,通过节点n到达Epoint的路径代价的估计值。A*算法的思想就是每次在多个候选节点中选择f值最小的节点进行扩展。
A*算法一般在搜索过程中构造两个表:open表和close表,其中,open表用于记录待扩展的节点,close表用于存放已经被扩展的节点[10]。在每步搜索过程中,首先从 open表中找出代价值最小的节点,将其加入 close表进行扩展。对扩展后的节点进行分析,根据分析结果对open表和close表进行修改,选择合适的扩展节点加入close表[11]。A*算法具有简单,易实现等优点,但算法计算量较大,不能很好的满足无人机动态规划的需求。

图1 搜索区域示意图
在二维平面内,本文创立了一种基于 A*的广义搜索算法。首先,把图1规定为上下左右四个方向;其次,把每一步的搜索区域限定在上,下,右,右上,右下这五个大方向,如图1所示,黑色矩形框中,中间六角星代表当前节点,五条线条表示搜索的五个方向,灰色区域表示整个搜索的大范围;其次,根据代价值判断子节点是否存在openlist列表中。这样,该算法不仅加快了规划时间,而且可以不断更新openlist来实时规划航路。
2 基于改进A*算法的动态航路规划
2.1 模型的建立
将空间离散化,设规划空间为 40*40的点阵,每一个点即为无人机航路搜索节点。如图2所示。

图2 规划空间模型
用黑色圆点表示威胁障碍和战场边缘,空白区域表示可行路径节点,图中加号表示无人机起飞点和目标点。在二维平面内,地理地形和地方雷达、威胁半径等约束可近似等效为一个圆,所以障碍威胁用圆点表示。航路规划的目的就是寻找一条从起点到目标点的飞行航路,且航路躲避敌方威胁,可以确保无人机安全高效的完成作战任务。那么航路点的集合即为完整的航路,表示为式(2):
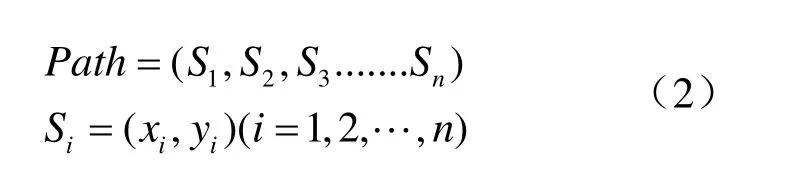
Path表示路径点集的集合,Si表示每一个路径的点,xi、yi分别表示每一个路径点的横坐标和纵坐标。
2.2 算法改进
启发式 A*搜索算法的基本思想是通过设定合适的启发函数,全面评估各扩展搜索节点的代价值,通过比较各扩展节点代价值的大小,选择最有希望的点加以扩展,直到找到目标节点为止。在传统A*算法的节点扩展中,节点扩展方式采用8个相邻的节点单元(图3中用“X”表示),这样不仅让节点扩展过于繁琐,算法的计算量也过大,航路不一定是最优,而且节点重复计算的比较多,使算法效率偏低。由于本文研究的是在二维平面内,考虑的约束模型比较简化,所以提出一种广义节点搜索法来替代以前的搜索方法。广义搜索法就是根据目标点和起始点的相对位置,确定目标点和起始点的连线方向,增加约束条件使搜索节点方向与连线的大方向一致,即朝着目标的方向搜索,这样不仅减少了节点搜索量,而且可以高效的找出最优路线,如图2所示,起始点和目标点连线的大方向即为右上方向;或者将搜索方向限定在上,下,右,右上,右下五个方向,如图1所示。根据A*算法的机理,搜索的节点应选取代价值最小的作为父节点。图 3中圈出的3个点的代价值必然是8个点中代价值较大的(规定正方向为右),因为它是向后搜索的,在航路的反向,所以去掉这3个点不仅不会影响航路,反而更加优化。如图3、图4所示,“+”表示当前节点,“X”表示搜索的相邻节点,圆点表示弃用的相邻节点。图4(a)为广义节点搜索的原始方法,图4(b)、图4(c)、图4(d)则是它演化而来,是它的一部分区域。
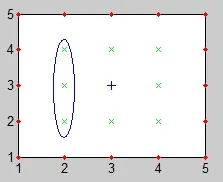
图3 传统A*搜索的节点
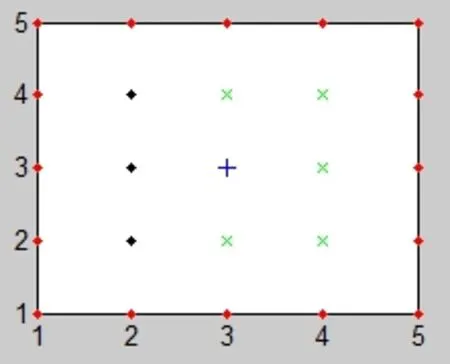
图4 (a) 广义节点搜索

图4 (b) 广义节点搜索
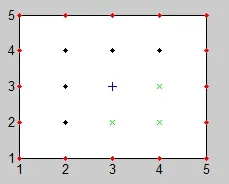
图4 (c) 广义节点搜索

图4 (d) 广义节点搜索
传统A*节点表示为式(3):

广义搜索法表示为式(4):

式(4)四个公式依次对应图 4中(a)、(b)、(c)、(d)。为当前父节点的坐标,根据i,j的取值范围可以确定搜索节点的位置(点阵的单位距离为1),式(3)和式(4)表示图3和图4中的灰色节点。
从图中可以清楚的看到,改进后的搜索扩展节点变少,这样可以大幅度缩减搜索空间,提高航迹规划效率。这在实际战场中有着重要意义,不仅缩短了作战时间,而且提高了无人机的寿命。
2.3 代价值重新估价
若要动态规划,那么就要重新估价代价值并进行判断,设当前点为Y,它的一个子节点为a,那么a的估价值为

C(Y,a)表示Y到a的距离,即
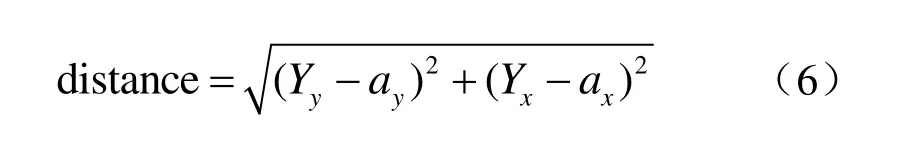
然后判断a是否存在于open和close中,如果a在open表中,那么比较当前a的g值和以前a的g值,取较小者,更新a的g值;同理,比较close表中的g值,如果a不在这两个表,则把a添加进open表,把Y添加到close表。流程图如图5所示。
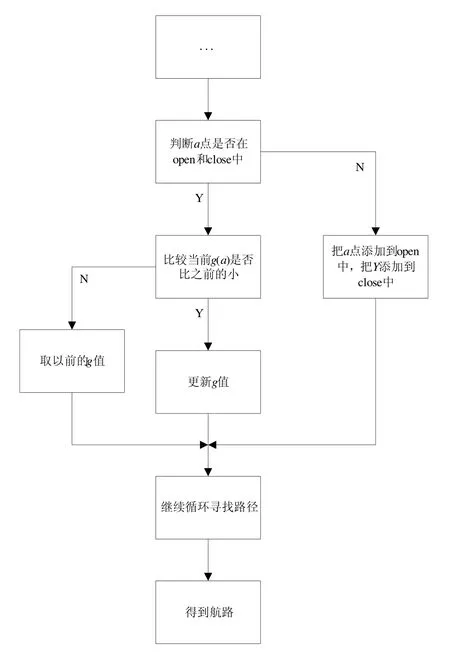
图5 重新估价代价值的流程图
3 仿真结果与讨论
本文用 MATLAB进行仿真,初始界面已经在模型建立中给出,航路起点为(2,2),终点为(38,34)。
(1)建立open和close表,把起点放入open中;
(2)寻找该点周围可到达的点,忽略已在close中的点;
(3)把该点添加到close表中;
(4)计算该点周围点的总代价值;
(5)找到代价值最小的点加入close中;
(6)重复2~5步骤直到目标点加入close中;
(7)将父节点画出得到航路。
结果如下。
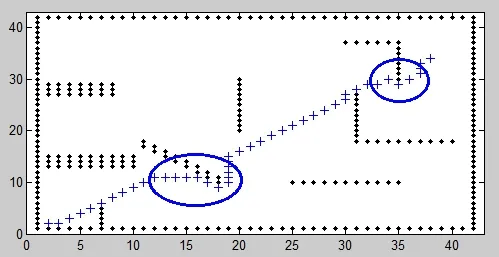
图6 A*算法的仿真

图7 改进后A*算法的仿真

表1 仿真结果
从图6圈中的地方以及图7的对比中可以看到,图6虽然成功避开了威胁,但是航路不合理,多绕了路,图7则非常简洁又避开了威胁。表1的数据可以清楚的反映出改进后的算法优于传统算法。
无人机在规划中会遇到突发威胁[13],文中将突发威胁用一段障碍(3个黑星号)表示出来,动态规划如图8所示。
比较图7和图8这两图,遇到突发威胁时,只对突发威胁附近的路线重新规划,其他区域路径不变,达到了良好的实时性。航路平滑处理后[12],得到一条光滑无尖角的曲线,如图9所示。
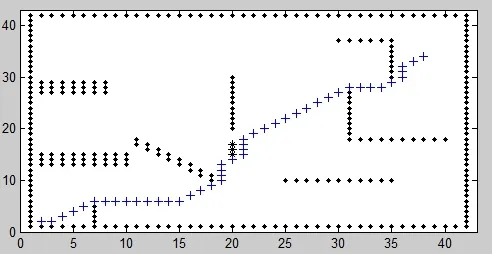
图8 动态规划

图9 平滑处理后的曲线
改进后的仿真结果清楚地表明,此无人机航路动态规划模型能够使无人机的作战效能达到最佳,生存概率极大,该模型是一种有效的模型,为无人机在复杂环境下的航路动态规划提供了一种有效地求解方法。
4 结论
本文针对无人机二维的动态航路规划问题进行了研究,根据动态航路规划的特性和文献建立了更加详细的航路规划空间模型,仿真实验表明。
(1)广义A*搜索算法不仅缩短了规划的时间而且优化了航路,同时在动态规划中,可以避开突发威胁并快速航路重规划,经过平滑处理后,规划航路没有尖角。
(2)该算法满足动态规划的需求,具有较强的工程实用性。
本文建立在二维模型上,有许多约束条件和一些代价问题不能直观的在图中显示,后续工作是建立精确的规划模型并将该算法扩展到三维甚至四维空间。
参考文献:
[1]刘森琪, 段海滨, 余亚翔. 基于 Voronoi图和蚁群优化算法的无人作战飞机航路规划[J]. 系统仿真学报,2008(21).
[2]李柠, 万顷浪, 刘福, 张殿富. 基于改进遗传算法的无人机协同航路规划[J]. 计算机测量与控制, 2013(08).
[3]刘慧卓, 杨金孝, 王泰然, 王鑫. 改进粒子群算法在三维航路规划中的应用[J]. 火力与指挥控制, 2013(11).
[4]王绪芝. 不确定环境下无人机航迹动态规划及仿真研究[D]. 南京航空航天大学, 2013
[5]卢江松. 基于改进蚁群算法的多机协同突防航迹规划方法研究[D]. 国防科学技术大学, 2012
[6]王铭谦. 基于蚁群算法的多无人机协同航路规划[J]. 计算机工程, 2001(S1).
[7]李季, 孙秀霞. 基于改进A-Star算法的无人机航迹规划算法研究[J]. 兵工学报, 2008(7).
[8]蒙波, 皮亦鸣, 曹宗杰. 基于改进A*算法的无人机航迹规划[J]. 计算机仿真, 2010(9).
[9]席庆彪, 苏鹏, 刘慧霞. 基于 A*算法的无人机航路规划算法[J]. 火力与指挥控制, 2013(11).
[10]杜萍, 杨春. 飞行器航迹规划算法综述[J]. 飞行力学,2005,23(2):10-14.
[11]George F Luger. 人工智能: 复杂问题求解的结构和策略(英文版. 第4版)[M]. 北京: 机械工业出版社, 2003.
[12]马云红, 周德云. 基于B样条曲线的无人机航路规划算法[J]. 飞行力学, 2004, 22(2):74-77.
[13]Lam Thu Bui, Zbignew Michalewicz, Eddy Parkinson,and Manuel Blanco Abello. Adaptation in Dynamic Environments: A Case Study in Mission Planning[J].Evolutionary Computation, Vol. 16, No. 2, April 2012
[14]Lanah Evers, Ana Isabel Barros, Herman Monsuur,Albert Wagelmans. Online stochastic UAV mission planning with time windows and time-sensitive targets [J].European Journal of Operational Research,238(2014)348–362

