深部采场进路开采顶板稳定性分析与支护设计*

戴怡文，王卫华，孙道元，张理维

(中南大学 资源与安全工程学院，湖南 长沙 410083)

0　引言

随着矿山浅部资源的枯竭，深部资源的安全高效开采已成为采矿行业的重大课题。衡量岩体稳定结构与井下安全作业的一项重要指标就是顶板稳定性情况及合理的支护形式。深部岩体的应力环境与工程地质条件相对于浅部要复杂的多，在采动、地压及地下水等多因素影响下，控制巷道围岩及顶板稳定性的难度更加艰巨[1-3]。因此，国内外学者展开了大量研究[4-6]，目前数值模拟法广泛应用于岩土与地下工程中，其能较好地克服传统工程类比与力学分析法不能完全反映岩体开挖后的应力-应变及实际破坏情况的不足[7-9]。

国外对采空区顶板稳定性分析和支护设计研究很多，特别是南非、澳大利亚、美国等国家，其数值模拟技术和支护理论均较完善[10-12]；国内虽然起步较晚，但发展迅速。周宗红等[13]结合矿山的实际开采条件，对采用分段空场崩落法时的护顶矿层与隔离矿柱进行了三维有限元模拟分析，选取了适合的护顶厚度与采场跨度，有效保证了空场顶板的稳定性。王新民等[14]利用ANSYS有限元分析软件模拟分析了柿竹园矿体典型采场顶板稳定性及采场围岩的力学状态，对地压进行了有效管理，实现了矿体的安全高效开采。

本文提出了适用于金属矿山“数值分析—围岩质量评价—动态监测”相结合的顶板控制技术。依据深部开采时所处的应力环境，对进路开采时巷道顶板稳定性进行数值分析，计算出进路开挖后顶板的最大拉应力、最大压应力及抗拉抗压系数。同时，结合矿区岩体质量评价，提出了具体的控制顶板位移变形的支护设计，优化了支护参数，并对现场支护效果进行动态监测。结果表明：该技术有效控制了顶板岩体位移变形，增强了顶板稳定性，为类似矿山顶板控制提供一定参考依据。

1　工程背景

1.1　矿体特征及采场布置

矿区主矿体分布主要受断裂蚀变带控制，赋存标高为+65～-750 m，矿体呈脉状，走向NE10～50°，倾向NW25～45°。单工程最大水平厚度12 m，最小水平厚度0.35 m，一般厚度1～3 m，平均厚度2.7 m。矿区-450 m以上矿体已开采完毕，-450～-530 m之间的矿体即将开采结束，-530 m中段及以下深部开采为后续矿山开采的工作重点。矿区一直沿用上向进路充填采矿法，采场沿矿体走向布置，采场宽度为矿体水平厚度，中段高度40 m，分段高度10 m左右。

1.2　岩体质量评价

为了分析顶板及围岩力学参数，对几个具有代表性的地点进行了工程地质调查。采用Q系统、RMR分类法和BQ分级法对岩体质量分级，得出矿区顶板在不同岩体条件下开挖后的稳定性评价，其结果见表1。

表1　矿区不同顶板分级结果Table 1　Grading results of different roof in mining area

由表1可知，3类岩体分级方法虽然侧重点不同，但对各区域岩体的质量评价大体相同。由此可知，矿区顶板主要为Ⅲ级岩体，介于一般岩体与较差岩体之间，岩体较破碎。

2　顶板稳定性数值模拟分析

2.1　岩体力学参数

由于裂隙、结构面对矿岩体强度有削弱作用，在有限元计算分析时采用强度折减系数法加以考虑[15]。数值模拟结果的可靠性在一定程度上取决于岩体的物理力学参数。通过对-490～-570 m的现场工程地质调查与室内岩石的物理力学实验，经折减后得到岩体的力学参数见表2。

表2　折减后岩体力学参数Table 2　Mechanical parameters of rock mass after reduction

2.2　数值模型构建及结果分析

构建数值模型时，为便于计算分析，对采场结构与开挖步骤进行适当简化。假设开挖岩体的厚度与倾角保持不变，矿岩体为理想弹塑性体。数值模拟关键区域为中段内最危险地段，即某中段内最下分层、最后三条二步回采进路。不同岩性顶板稳定性物理模型结构参数如表2所示。实体模型及网格划分如图1所示。关键区域实测尺寸为15 m×3 m×30 m，构建模型尺寸为关键区域的5～10倍，即：105 m×21 m×210 m。分别对-490～-570 m回采进路6个模型的顶板稳定性情况进行模拟分析，各水平进路尺寸及计算结果见表3。

结果表明：

1)矿区岩体在开挖后进路顶板中均出现拉应力，主要集中在进路与上盘围岩的接触面上，模型3的最大拉应力最小，为0.24 MPa;模型2的最大拉应力最大，为1.24 MPa。

图1　有限元分析模型Fig.1　Model diagram of finite element analysis

模型序号岩性进路尺寸/(m×m×m)Y方向位移/mm最大拉应力/MPa最大压应力/MPa抗拉稳定系数η1抗压稳定系数η21黄铁化绢英岩(-490m)3×3×30-256008081490941292钾化花岗岩(-530m)3×3×30-185112401342194193黄铁化绢英化花岗岩(-530m)3×3×30-292002401492500994硅化钾化花岗岩(-530m)3×3×30-245707331532322645黑云母花岗岩(-570m)3×3×30-324404891631330966黄铁化绢英化花岗岩(-570m)3×3×30-29211130173072140

矿区顶板的最大拉应力整体趋势表明，岩体开挖后所出现的拉应力会随着开挖深度的增加而小幅增加。由表3中抗拉稳定性系数可知：2，3，4号模型抗拉系数介于2～3之间，表明稳定性较理想;1号和6号模型抗拉稳定系数均小于1，表明这2种岩体在开挖后，顶板表现非常不稳定，有可能会发生冒顶事故。

2)岩体开挖后，模型1，2，4，6的进路与上盘围岩接触端面处出现最大压应力，顶板的压应力会随着采深的增加而增大；模型2，4抗压系数较大，岩体的稳定性较好，安全性较强；模型3，5抗压系数低于临界状态，存在安全隐患。

3)由顶板暴露面处Y方向位移值可知，位移较大的区域，岩体更接近松弛区，当开挖后顶板发生应力集中导致拉应力超过岩石抗拉强度时，顶板岩层将最先在此区域产生拉裂缝，拉裂缝逐渐延伸扩大导致顶板失稳。

3　支护设计及现场监控

3.1　支护方案设计

选用管缝式锚杆，钢材强度二级以上，长1.8 m，厚2 mm，直径40 mm，锚杆极限抗拉力110 kN。结合矿区开采实际条件、岩体质量分级、数值模拟及相关工程经验，针对Ⅲ级围岩，临时巷道，采用锚杆支护，潜在可移动块体区域，配置穿带进行支护，永久巷道，采用锚喷支护。

3.2　支护参数优化

为确保巷道安全，结合经济成本，巷道安全系数设计值取1.5。引用悬吊理论、组合梁理论和屈服强度理论优化支护参数[16]，其安全系数表达式分别为式(1)～(3)：

(1)

(2)

(3)

式中：ρ为覆岩密度，kg/m3；g为重力加速度，m/s2；Pf为极限抗拉力，kN；tloose为松动圈厚度，m；n为每平方米锚杆数量；Ttotal为组合梁抗剪承载力，kN；τmax为最大剪切应力，kN；k为每排锚杆数量；Pbolt为锚杆屈服强度，kN；L为巷道宽度，m；d为锚杆排距，m。

对不同锚杆间距时排距与安全系数的变化关系进行分析，其结果分别如图2～4所示。

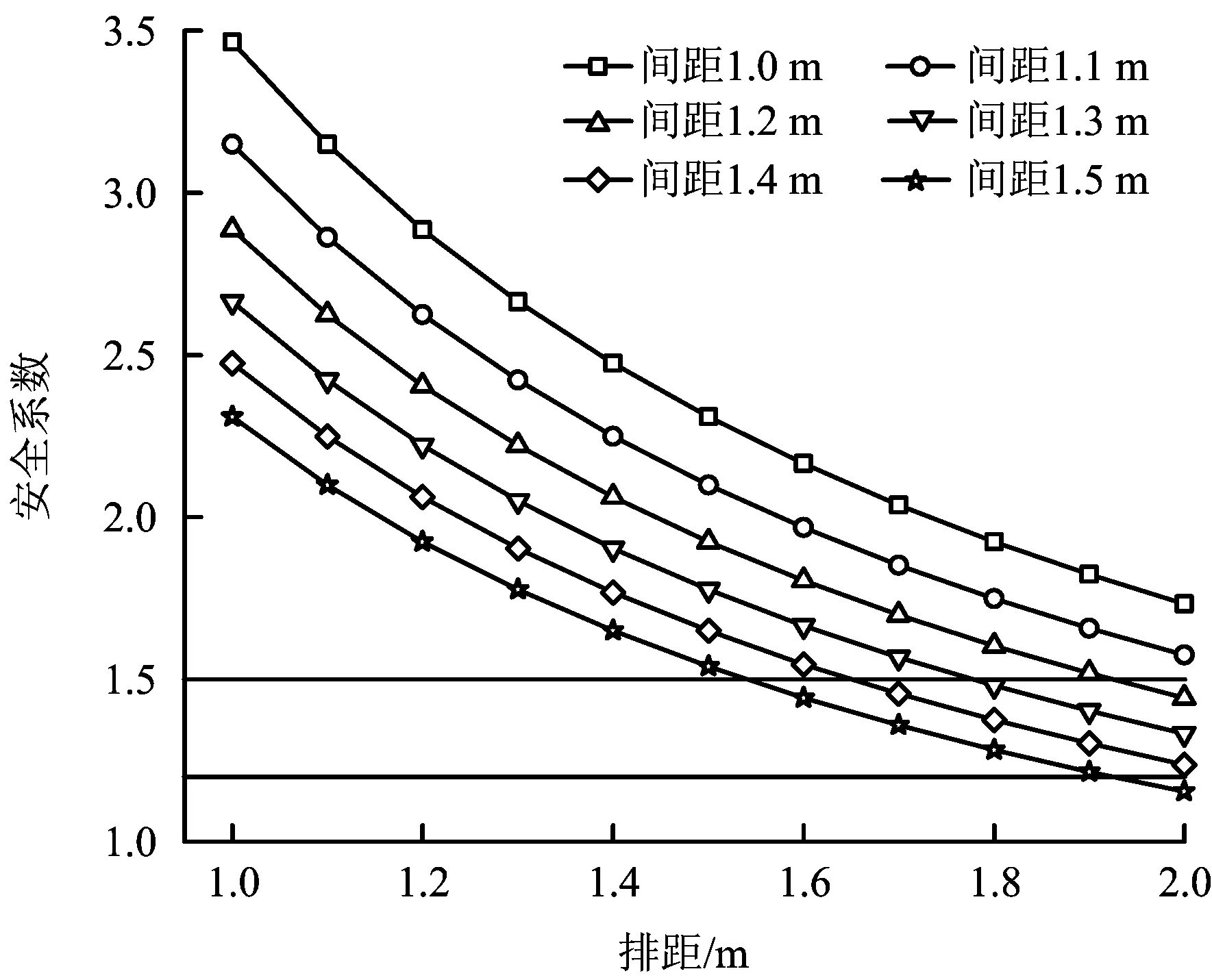
图2　悬吊理论-不同锚杆间距时安全系数与排距的关系Fig.2　Suspension theory-relationship between safety factor and row spacing in different bolt spacing

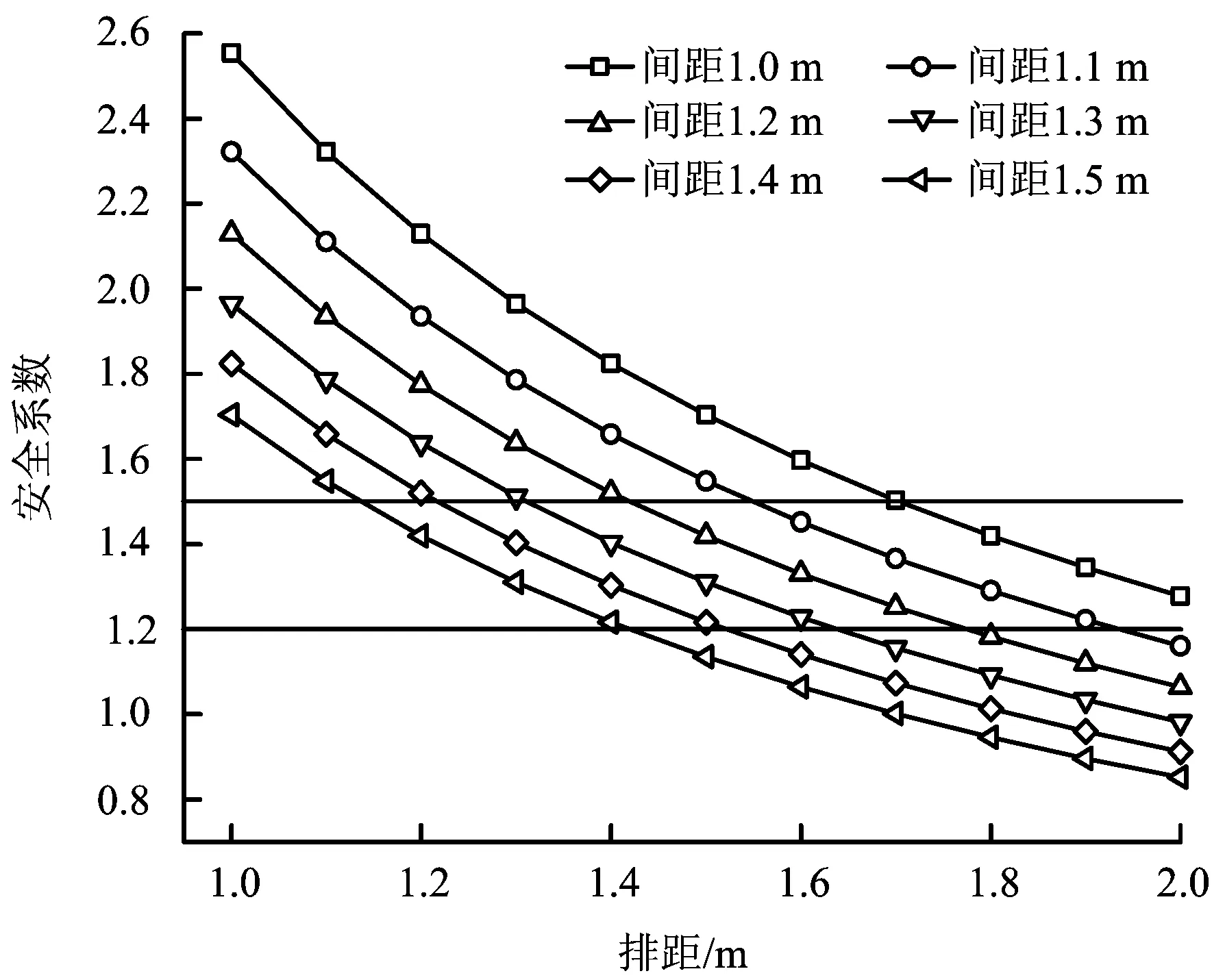
图3　组合梁理论-不同锚杆间距时安全系数与排距的关系Fig.3　Composite beam theory-relationship between safety factor and row spacing in different bolt spacing

图4　屈服强度理论-不同锚杆间距时安全系数与排距的关系Fig.4　Yield strength theory-relationship between safety factor and row spacing in different bolt spacing

由图2～4可知，锚杆相同间距，不同排距时，组合梁理论求出的安全系数最小，悬吊理论求出的安全系数最大。综合3种支护参数优化结果：临时巷道，锚杆支护拱顶，间距1 m，排距2.5 m，潜在可移动块体区域(如倒三角块体不能通过撬毛解决)配置串带；永久巷道，锚喷支护拱顶，间距1 m，排距2 m。

3.3　现场监测

为探究深部岩体开挖后围岩应力变化情况及支护效果，分别选择了2个具有代表性的区域安装了2根振弦式锚杆应力计，其结构如图5所示。1号锚杆应力计安装在有锚杆支护的巷道中，2号锚杆应力计安装在未采用任何支护的巷道中。

图5　振弦式锚杆应力计的外形及构造Fig.5　Shape and structure of vibrating wire anchor stress gauge

安装调试完成后，采集一组数据作为初始数据，然后接着进行数据采集。为了避免一段时间内采集数据过多，导致数据无法导出，每隔3～5 d进行一次数据拷贝工作，并清除采集仪中前期采集到的数据，继续进行采集工作。数据采集完成后，通过计算分析，获得1，2号锚杆应力计的轴向应力如图6所示。

图6　振弦式锚杆应力计各传感器轴向力变化情况Fig.6　The axial force change of each sensor of vibrating wire anchor stress gauge

由图6可知：1号锚杆应力计3个传感器上的轴向力均表现为拉应力，且轴向力逐渐增大，随着时间的变化，轴向力的增长速率逐渐平缓，巷道围岩中应力逐渐趋于稳定；2号锚杆应力计上的轴向力明显大于1号锚杆应力计上的轴向力，且增长速率明显大于1号传感器上轴向力增长速率，围岩应力呈现持续增大的趋势。开挖后若不及时进行支护，随着围岩中应力的变化及重新分布，容易造成冒顶及片帮等事故发生。监测结果表明：锚杆支护对开挖后岩体变形起到了明显改善作用。

4　结论

1)采用Q系统、RMR分类法和BQ分级法进行岩体质量分级，综合了各分级方法的优点，分级结果能更加准确地描述围岩及顶板稳定性情况，为顶板有限元模拟分析提供矿岩数据。根据分级结果，岩体稳定性处于一般至较差之间，局部有垮落隐患。

2)应用数值模拟软件，对-490～-570 m水平顶板进行分析计算，结果表明，矿区存在着部分岩体顶板稳定性较差的区域，在进路顶板处出现较大拉应力集中区，抗拉稳定系数较低，极有可能出现顶板冒落现象。

3) 采用“数值分析—围岩质量评价—动态监测”相结合的地压管理手段，针对Ⅲ级围岩，提出了锚杆支护方式，同时运用悬吊理论、组合梁理论、屈服强度理论优化了支护参数，并通过振弦式锚杆应力计进行现场监测，取得了良好工程效果，为类似矿山顶板控制提供一定借鉴经验。

[1] HUANG Z P, BROCH E, LU M. Cavern roof stability-mechanism of arching and stabilization by rockbolting[J].Tunnelling and Underground Space Technology,2002,17 (3):249-261.

[2] 柏建彪,侯朝炯.深部巷道围岩控制原理与应用研究[J].中国矿业大学学报,2006,35(2):145-148.

BAI Jianbiao, HOU Zhaojiong. Control principle of surrounding rocks in deep roadway and its application[J]. Journal of China University of Mining and Technology, 2006, 35 (2): 145-148.

[3] 侯朝炯.巷道围岩控制[M].徐州:中国矿业大学出版社,2013.

[4]许梦国, 郭廖武. 锚杆联系链在复杂地质条件下巷道支护中的应用[J]. 黄金, 2000,21(9):11-14.

XU Mengguo，GUO Liaowu.Application of bolt connecting chain in tunnel support under complex geological conditions[J]. Gold, 2000, 21(9): 11-14.

[5] 李英明,贾安立,马念杰. 煤巷顶板岩层赋存特征及块体梁顶板稳定性分析[J].中国安全生产科学技术,2014,10(6):51-57.

LI Yingming, JIA Anli, MA Nianjie. Analysis on occurrence characteristics of roof strata in coal roadway and stability of blocks rock beam roof[J]. Journal of Safety Science and Technology, 2014, 10 (6): 51-57.

[6]BROOK N, DHARMARATNE P G R. Simplified rock mass rating system for mine tunnel support[J]. Institution of Mining and Metallurgy Transactions, 1985, 94.

[7] 马念杰,赵希栋,赵志强,等. 深部采动巷道顶板稳定性分析与控制[J].煤炭学报,2015,40(10):2287-2295.

MA Nianjie, ZHAO Xidong,ZHAO Zhiqiang, et al. Stability analysis and control technology of mine roadway roof in deep mining[J]. Chinese Journal of coal, 2015, 40 (10): 2287-2295.

[8]VLACHOPOULOSN, DIEDERICHS M S. Appropriate uses and practical limitations of 2D numerical analysis of tunnels and tunnel support response[J]. Geotechnical and Geological Engineering, 2014, 32(2): 469-488.

[9] 曹平,王飞,邱冠豪,等.软岩大变形巷道支护技术及应用[J].中国安全生产科学技术,2014,10(8):69-74.

CAO Ping, WANG Fei, QIU Guanhao, et al. Support technology and its application for large deformation of soft rock roadway[J]. Journal of Safety Science and Technology, 2014, 10(8): 69-74.

[10] HU G Z, WANG H T, LI X H, et al. Numerical simulation of protection range in exploiting the upper protective layer with a bow pseudo-incline technique[J]. Mining Science and Technology, 2009, 19(1):58-64.

[11] SRIVASTAVA L P, SINGH M. Effect of fully grouted passive bolts on joint shear strength parameters in a blocky mass[J]. Rock Mechanics & Rock Engineering, 2015, 48(3):1-10.

[12]HAILE A. T. Observations of the dynamic performance of South African tunnel support systems[J]. Rock Support and Reinforcement Practice in Mining,1999, 335.

[13] 周宗红,候克鹏,任凤玉.分段空场崩落采矿法顶板稳定性分析[J].采矿与安全工程学报,2012,29(4):538-542.

ZHOU Zonghong, HOU KePeng, REN Fengyu. Roof stability analysis of sublevel open stope and caving mining method[J]. Journal of Mining & Safety Engineering, 2012, 29(4): 538-542.

[14]王新民,王长军,张钦礼,等. 基于ANSYS 程序下的采场稳定性分析[J].金属矿山,2008(8):17-20.

WANG Xinmin, WANG Changjun, ZHANG Qinli, et al. ANSYS-based stability analysis of stope[J].Metal Mine, 2008(8):17-20.

[15] 杨宇江,庄文广,王照亚,等.基于强度折减法的地下采场稳定性分析[J].东北大学学报(自然科学版),2011,32(6):864-867.

YANG Yujiang, ZHUANG Wenguang, WANG Zhaoya, et al. Stability analysis of underground stope based on strength reduction theory[J]. Journal of Northeastern University (Natural Science), 2011, 32(6): 864-867.

[16] CANBULAT I, VANDER MERWE J.N. Design of optimum roof support systems in South African collieries using a probabilistic design approach[J]. The Journal of the Southern African Institute of Mining and Metallurgy, 2009,108:71-88.