露天矿运输问题的模拟退火优化
彭 程,薛伟宁,黄 轶
(1.华北科技学院信息与控制技术研究所,河北 三河 065201;2.安全监测监控技术国家安全生产监督管理总局安全生产重点实验室,河北 三河 065201)
随着能源价格的变化,运输优化成为露天矿企业降低生产成本、提升竞争力的重要手段。运输问题是一类特殊的线性规划问题,可以利用单纯形法或内点法等传统的线性规划算法求解。近年来智能优化领域的研究取得了很大进展,学者将智能优化算法用于求解露天矿运输问题。例如文献[1]~[3]分别采用遗传算法优化的神经网络、双目标粒子群优化算法和混合差分进化-生物地理优化算法进行了露天矿运输问题的优化计算。与单纯形法等传统的线性规划问题解法相比,智能优化算法的性能还有差距,但是这类算法的优势在于易于理解和实现,并且可以进一步推广到更复杂的运输优化问题中[4]。与文献[1]~[3]直接对运输量进行优化的思路不同,文献[4]利用运输问题的特点,将运输问题表示为生成可行解的排序优化问题,并利用遗传算法求解排序优化问题,取得了较好的效果,但是遗传算法在交叉操作的过程中会生成不合理的解,需要进一步调整。
模拟退火算法[5]能够以一定的概率接受变差的解,具有跳出局部极小点的能力,是一类重要的全局优化算法,已被用于解决旅行商[5]、振动系统频域辨识[6]以及超分辨率图像重建[7]等各类问题。用其求解旅行商问题等排序优化问题时,不需要进行解的进一步调整。为此,本文采用了文献[4]的将运输问题转化为等价的排序优化问题,并使用智能优化算法求解的思路,实现了模拟退火算法进行露天矿运输的优化计算,并与文献中报道的结果进行了对比。
1 问题描述
假设露天矿有I个装载点,分别表示为Li(i= 1,2,…,I),装载点Li所在采区的开采能力为Pi,m3;J个卸载点,分别表示为Uj(j=1,2,…,J),卸载点Uj的受矿能力为Qj,m3。则为了降低运输成本,露天矿运输问题的目标函数定义为式(1)。
(1)
式中,Cij和xij分别为从装载点Li到卸载点Uj的单位运费和运输量,Cij单位为元/m3,xij单位为m3。
假设装载点所在矿区生产的矿石需全部运出,卸载点接收的矿石量不大于其受矿能力,运输问题还需要满足等式约束(式(2))和不等式约束(式(3))。考虑到实际的运输过程中运输量xij不能为负,故运输问题还需满足边界约束,见式(4)。
(3)
xij≥0,i=1,2,…,I,j=1,2,…,J
(4)
综上,本文研究的露天矿运输问题可以表示为式(1)~(4)定义的约束优化问题。

由装载点LI+1到各卸载点的运输量分别为xI+1,1、xI+1,2、…、xI+1,J,运费均为0,元/m3,则式(1)~(4)定义的非平衡运输问题等价于式(5)定义的平衡运输问题。
2 运输问题的排序优化表示
在运输问题中使用智能优化算法的通常做法是直接对运输量xij进行优化,但这样处理存在着难以满足约束条件,尤其是等式约束条件,进而陷入局部极小点的困难。运输问题的一类经典解法是表上作业法[8],它有不同的实现形式,如最小元素法,伏格尔法等。当运输问题自变量的数量较多时,表上作业不太方便。文献[4]借鉴表上作业法的思想,提出了将运输问题转化为排序优化问题的思路,使得运输问题的约束条件可以直接得到满足。本文也使用了这一思路处理露天矿运输问题。下面以一个简单的运输问题为例,说明排序操作的过程。详细的原理可以参考文献[4]和文献[8]。
假设某厂有位于不同地区的2个分厂,生产相同品质的一种产品,每天的产量分别4 t和6 t;销往3座城市,3座城市每天销量分别为3 t、2 t和5 t;从1分厂到3座城市的单位运费分别为200元/t、500元/t和100元/t,从2分厂到3座城市的运费分别为300元/t、200元/t和300元/t。总产量和总需求量均为10 t/d,故该运输问题是平衡的,可以表示为如下的线性规划问题。
minf(x)=200x11+500x12+100x13+
300x21+200x22+300x23
s.t.x11+x21=3,x12+x22=2,
x13+x23=5,x11+x12+x13=4,
x21+x22+x23=6
为了生成可行解,需要将运输量放入图1中的按照产地为行,销售地为列的表中,表中最后一行为各销售地的总销量,最后一列为各产地的总产量。将图1中6个空白位置按行进行编号,表示为1~6,例如第一行第二列的空白位置编号为2,第二行第一列的空白位置编号为4,等等。
假设首先在图1中编号为3的空白位置,即第一行第三列放入一个运输量,考虑到1分厂产量为4 t,城市3的销量为5 t,故运输量取其中较小的值,即4 t;同时将第一行和第三列允许的运输量各自减去放入位置3中的4 t,即图1变为图2。
同理,假设第二次在图2中编号为2的空白位置,即第一行第二列放入一个运输量,其取值为所在行和列允许的运输量的较小值,即0t;同时将第一行和第二列允许的运输量各自减去放入位置2的0t,即图2变为图3。
假设之后按照6、4、5、1的顺序依次修正运输量作业表,得到图4,图中最后一行和最后一列均为0,即此时得到了优化问题的一个满足约束条件的解。

46325-

图1 原始运输量作业表

图2 一步之后的运输量作业表
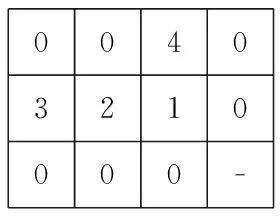
图3 二步之后的运输量作业表
图4六步之后的运输量作业表
实际上图4中的运输量为该运输问题的最优解,对应的最优运费为2 000元。它可以由上述的作业顺序S=[3,2,6,4,5,1]生成。作业顺序不同,最终得到的运输量不同,但是都能够满足约束条件。平衡运输问题的解可以通过找到最优作业顺序的方式得到。
3 运输问题的模拟退火优化
对于小规模问题,表上作业法是有效的,但是自变量数目较多时,表上作业不太方便。考虑到模拟退火算法是解决排序优化问题,例如旅行商问题的有效方法,本文实现了模拟退火算法进行作业顺序的优化。
模拟退火算法主要包括生成及接受/抛弃新解和降温两类操作。
1) 生成及接受/抛弃新解操作。对每个特定的温度,在已有解的基础上按照某种方式生成一个新解,若新解优于已有解,则接受该新解。若新解劣于已有解,则按照一定概率接受新解,接受概率与当前所处温度有关,温度越高,接受的概率越大。在当前温度下执行若干次生成新解、接受/抛弃新解的操作,以达到在该温度下的平衡。
2) 降温操作。从一个足够高的温度出发,按照某种规律进行降温。
不同的模拟退火算法的主要区别在于生成新解的方式以及降温方式不同。本文采用几何降温方式。
作业顺序优化是一类排序优化问题,假设已有一个作业顺序S0,生成新的作业顺序的一种方法是在S0中任选两个位置,交换两位置的内容,其他位置的内容保持不变。例如对上述运输问题而言,假设原有的作业顺序为S0=[1,3,2,5,4,6],随机产生的位置为2和4,则交换位置2和位置4的内容,可以生成一个新的作业顺序S1=[1,5,2,3,4,6]。
综上,求解露天矿运输问题的模拟退火算法的步骤,如下所示。
1) 步骤一,增加虚拟装载点,将式(1)~(4)定义的非平衡运输问题转化为式(5)定义的平衡运输问题。
2) 步骤二,设定模拟退火算法参数,包括初始温度T0、终止温度T2、降温系数α、每个温度下生成新解的最大次数N。
3) 步骤三,随机生成一个作业顺序S0,计算对应的可行解x0以及对应的运费f(x0)。令当前温度T1=T0,已生成新解数目n=0。令最优解xb=x0,最优目标函数fb=f(x0)。
4) 步骤四,在已有的作业顺序S0中任意找到两个位置,交换其内容,其他位置保持不变,生成新的作业顺序S1;计算对应的可行解x1以及对应的运费f(x1)。若f(x1)
5) 步骤五,令当前温度T1下已生成新解的次数n=n+1。若n 6) 步骤六,按几何方式进行降温,即令温度T1=αT1。若T1>T2,令已生成新解数目n=0,返回步骤四;否则输出最优解xb及其对应的最优运费fb。 为了验证模拟退火算法求解露天矿运输问题的效果,考虑文献[1]、文献[2]研究过的抚顺西露天矿运输问题,该矿有9个装载点、5个卸载点,各装载点所在采区的开采能力、卸载点的受矿能力、从各装载点到各卸载点的单位运费数据见表1。经计算,总受矿能力比总开采能力大150万m3,故该运输问题是非平衡的,需要引入第10个虚拟的装载点,其对应的开采能力为150万m3,到各卸载点的运费均为0元/m3。该露天矿运输问题可以表示为一个十行五列的运输量作业表上的排序优化问题。 模拟退火算法的参数:初始温度T0=1 000 ℃、终止温度T2=1 ℃、降温系数α= 0.999、每个温度下生成新解的最大次数N=3。模拟退火算法求出的最优解见表2,对应的最优运费为41 224万元。表2同时给出了文献[1]、文献[2]求出的最优解,对应的最优运费分别为41 717万元和44 090万元。借助于Matlab软件提供的线性规划求解器linprog得到的最优运费为41 224万元,对比可知模拟退火算法得到了该运输问题的全局最优解。 表1 抚顺西露天矿运输问题数据表 表2 不同算法得到的抚顺西露天矿运输问题的最优解 为了考察上述参数对本文实现的模拟退火算法性能的影响,重复进行100次优化计算,100组最优解中,有99组为41 224万元,1组为41 232万元,这表明优化计算中使用的算法参数是合理的,能够使模拟退火算法具有较好的可重复性。 本文借鉴了文献中将运输问题转化为排序优化问题的思路,利用模拟退火算法求解露天矿运输问题。实现的模拟退火算法在生成新解时只需进行简单的位置交换操作,具有易于理解和实现的优点。计算结果表明,通过合理设置参数,模拟退火算法可以得到运输问题的全局最优解,是求解露天矿运输问题的一种有效算法。 [1]鞠兴军,李林,刘光伟.基于遗传算法的神经网络在露天矿卡车调度系统中的应用研究[J].露天采矿技术,2009,24(6):31-33. [2]李勇,胡乃联,李国清.基于改进粒子群算法的露天矿运输调度优化[J].中国矿业,2013,22(4):98-101,105. [3]王桃,江松,卢才武.露天矿运输调度优化的生物地理学改进算法[J].金属矿山,2016(9):161-164. [4]VIGNAUX G A,MICHALEWICZ Z.A genetic algorithm for the linear transportation problem[J].IEEE Transactions on Systems,Man and Cybernetics,1991,21(2):445-452. [5]KIRKPATRICK S,GELATT C D,VECCHI M P Jr.Optimization by simulated annealing[J].Science,1983,220:671-680. [6]彭程,王永.振动系统稳定模型的频域辨识[J].振动与冲击,2010,29(3):118-120. [7]任宏德.基于模拟退火算法优化的超分辨率图像重建[J].激光杂志,2016,37(2):38-41. [8]夏伟怀,符卓.运筹学[M].长沙:中南大学出版社,2011:75-86.4 计算实例

5 结 语

