船闸卧式闸门水位控制建模与控制策略研究
李建宜,李端明,史旺旺
(1.扬州大学水利与能源动力工程学院,江苏 扬州 225127;2.中国灌溉排水发展中心,北京 100000)
0 引 言
平面卧式闸门是一种可以绕安装在门槽底的转动轴转动,双向进水,以适应不同水位和流量的控制要求的闸门。闸门的启闭采用安装在闸墩两侧的液压启闭机系统,闸门全开时隐没在水下门库内,不干扰水流;闸门挡水运行时,当到达一定的开度时水流从闸门顶部与底部溢流。平面中枢卧式闸门使用在船闸系统中,可以不再建造船闸过水廊道,大大减少了水工建筑物的投资,优化了船闸闸室结构,适合在一般中小型船闸结构中使用。但是,由于平面卧式闸门在启闭过程中上下两部分均可以过流,导致流态复杂,特别在船闸过船过程中,如果闸门开启过快,闸门的位置状态在短时间内发生较大变化,会引起闸室流场的巨大变化,对闸室翼墙的安全与闸室内的船舶直接构成威胁,而且非稳定流的骤增对下游的安全也十分不利;如果闸门开启过慢,又影响船闸通行效率。因此,需要根据水工模型试验研究结果,结合现代控制优化运行方法,在保证不同水位差下船闸充放水时闸室内的水流流速均能满足船只安全通行的前提下,动态控制船闸启闭机的运行速率,优化不同水位条件下船闸运行通行能力,从而充分挖掘船闸通航能力的潜力。因此,研究设计根据闸室流量流速来决定闸门开启速度的动态控制方法是十分必要的。
船闸水位控制的目的是使得船闸闸门上下游水位差为0。在定频控制的闸门控制系统中,通过开关控制方式进行[1]。随着电力电子技术的发展,变频调速在闸门控制中也逐渐得到应用。该技术的应用提高了闸门控制的性能,也对闸门控制技术提出了更高的要求。闸门控制的主要方法是PID算法[2,3],该算法在过闸流量大且需要限流的场合应用效果差。如果控制和输出之间存在延时,施密斯预估方法可以补偿此延时[4,5]。其他新型控制策略如模糊控制、神经网络优化控制方法也在水位控制得到应用[6-9]。
本文在对船闸模型进行数学分析的基础上,建立了以水位差的开根号为输出,以频率为输入的传递函数模型,并设计了PID控制算法。针对常规PID控制限流困难,提出了流量内环水位外环的PID控制策略,保证过闸流量不超过最大值,同时避免了闸门动作频繁。以流量为内部控制变量的控制模型本质上属于非线性系统,为此提出基于反步法设计的非线性控制方法,达到快速且稳定的控制效果。
1 船闸闸门控制模型
设船闸闸室面积为S,闸门内外水位差为H,闸室内水量为SH,过闸流量为Q,根据水量平衡得:
(1)
根据水力学理论,流量Q与水位差H和闸门开度hg满足如下关系:
(2)
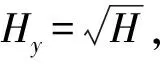
(3)
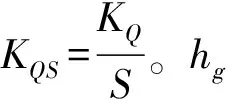
(4)
闸门运动速度v由变频器的输出频率u控制, 电机的电流响应速度比闸门速度响应快,频率到闸门速度输出可近似为一阶惯性环节,即:
(5)
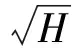
(6)
闸门控制的主要目标使上下游水位差尽快趋向于0,同时保证整个控制过程中流量不能超限;闸门在开启过程中避免开启速度变化过大,禁止闸门在上升过程中出现短时下降,此要求容易引起流量超限。
2 基于PID的控制算法
2.1 常规PID控制
常规PID控制以输出值 作为控制变量,控制结构图如图1所示。
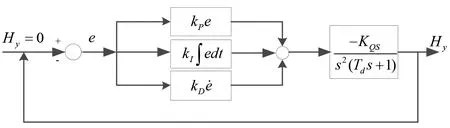
图1 常规PID控制结构图
过闸流量Q作为隐含变量没有直接控制,因此在控制初期,水位差较大,容易引起流量超限。在控制过程中,通常采用保护策略,即当Q>Qmax时,令控制变量为0,使变频器输出频率为0,闸门停止运行。待水位下降后流量不超限时继续调节过程。图2位为常规PID控制策略同时采用流量超限保护策略的控制结果图。图2中(a)为闸门水位差过程曲线,(b)为过闸流量过程曲线,(c)为闸门开度过程曲线,(d)为闸门速度过程曲线。控制中极限流量Qmax=5 m3/s。
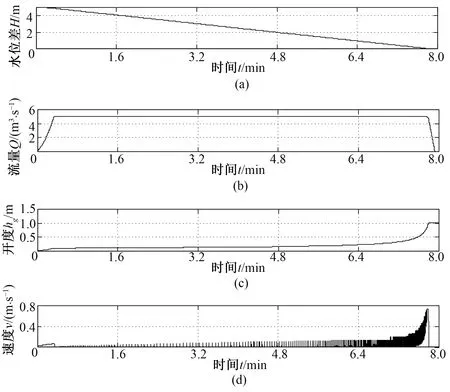
图2 常规PID控制过程曲线
从图2(c)、(d)可以看出:虽然过闸流量没有超限,但控制过程中出现了频繁的保护,引起闸门速度波动,这极易引起系统机械磨损,减小了系统寿命。
2.2 双闭环常规PID控制
为使流量不超限,流量应作为控制变量,为内环被控量。外环水位误差经PID调节后,得到的输出为内环流量的设定值。在内环中,流量误差经PID调节后得到控制量u。控制原理如图3所示。内环中流量值与水位差存在耦合,为非线性关系,控制关系不明显。当实际流量小于设定流量时,可通过增加闸门开度,即增加变频器频率实现,其控制关系符合常规控制,因此采用经典的控制方式具有一定的适用性。
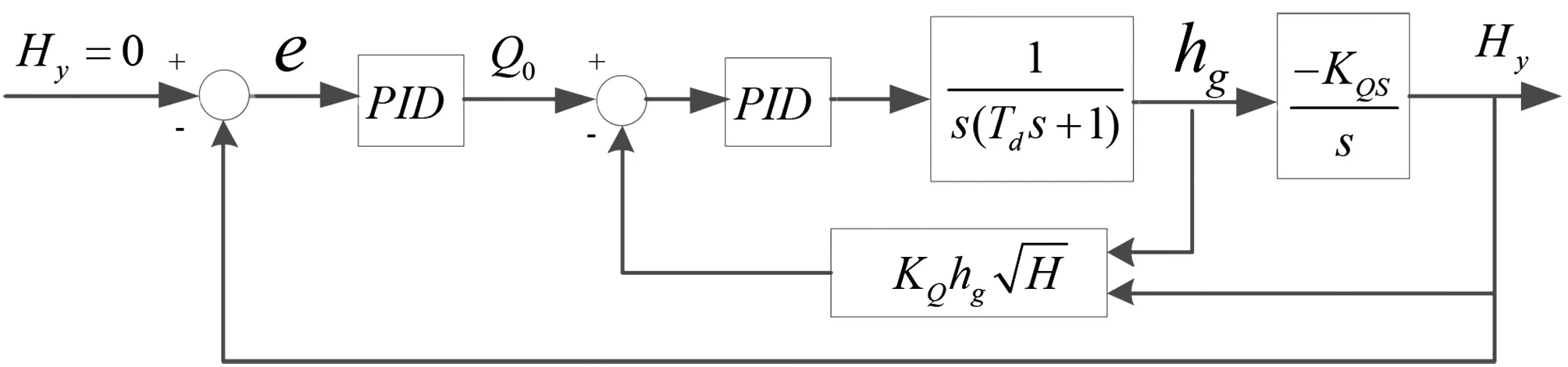
图3 双闭环控制结构图
3 基于Lyapunov法的非线性控制
由于内环流量与外环水位差之间存在非线性耦合,采用PID线性控制方法很难保证系统全局收敛,需要采用非线性控制设计方法才能保证系统稳定性和性能。基于Lyapunov稳定性理论的反步法设计方法是非线性设计的一种重要和实用方法,可以保证系统全局收敛。反步法设计方法的核心是分步设计Lyapunov函数。根据Lyapunov稳定性理论,应先定义一个正定的纯量函数,通过控制使得该函数收敛到0时,相应的变量收敛到对应的平衡点。
定义Lyapunov函数:
(7)
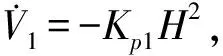
(8)
式(8)中Kp=Kp1S,Ki=Ki1S。
考虑到最大流量约束,如果Q0>Qmax,赋值Q0=Qmax,转换成hg0得:
(9)
如果Q=Qmax,则:
(10)
对于内环,定义Lyapunov函数 :
(11)
求导,得:
(12)
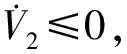
(13)
整理得:
(14)
其中:
(15)
若Q=Qmax则:
(16)
4 仿真验证及分析
为验证控制算法的正确性,利用MATLAB仿真平台,将双闭环控制算法和非线性控制算法进行仿真并进行对比。船闸闸室参数如表1所示。

表1 闸室参数表
仿真结果如图4所示。图中,虚线表示双闭环控制的仿真结果,实现表示本文非线性控制算法的仿真结果。由图4可以看出,两种控制算法均保证流量没有超限,闸门上升速度曲线光滑,满足闸门控制要求。但非线性控制算法的流量曲线更加平滑,在限流阶段流量曲线接近一条水平直线,过闸流量保持在5 m3/s,稳流效果比双闭环控制效果好。在6.4 min后,水位差小,流量已不会超过最大流量时,非线性控制方法中的闸门速度响应比双闭环控制中闸门速度快,因此非线性算法的调节时间比双闭环短,且速度没有大的波动,克服了常规控制的缺点。
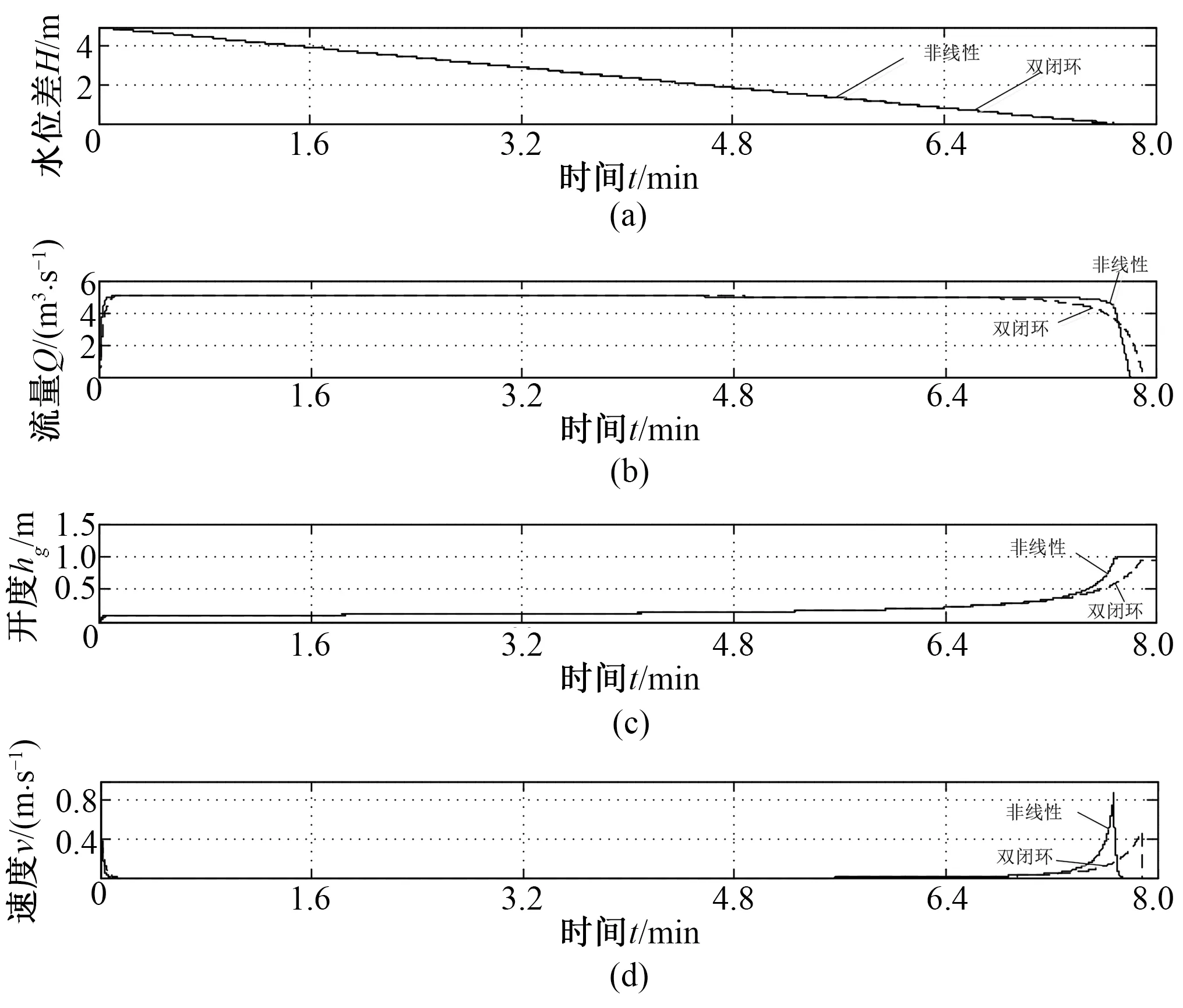
图4 双闭环和非线性控制结果图
5 结 论
通过对对船闸数学模型数学分析,以水位差的开平方为被控对象的系统为线性系统。在采用变频调速的船闸且过闸流量大的场合,需要通过调节闸门开度保证流量不大于最大过闸流量,采用常规PID控制方难以保证流量不超限。双闭环控制算法和基于反步法的非线性算法均能实现限流控制,但非线性控制策略在快速性和稳定性上具有更大的优势。
□
参考文献:
[1]王玉明,颜亚琴.门底充水式船闸计算机控制系统的应用[J].江苏水利,2015,(11):44-48.
[2]陈海霞,任庆海,英小勇.PID算法在船闸控制系统中的应用[J].水利信息化,2011,(6):49-52.
[3]胡志生.PID调节与V型滤池恒水位控制[J].微计算机信息,2012,(9):103-104.
[4]张宇,范延滨.基于MATLAB的水箱液位控制系统的研究[J].工业控制计算机,2016,(11):59-63.
[5]徐杰,吴夏来.施密斯预估方法在单容水箱液位控制中的应用[J].丽水学院学报,2013,(5):51-54.
[6]张晓莉,杜文玉.基于PLC系统的双容水箱液位控制[J].2017,(17):1-7.
[7]宋清昆,曹剑坤,韩笑,等.关于三容水箱系统水量液位优化控制研究[J].2016,(5):330-334.
[8]Pan H Z.Experimental validation of a nonlinear backstepping liquid controller for a state coupled two tank system [J].Control Enginerring Practice, 2005,13:27-40.
[9]Horton E C, Foley M W, Kwok K E.Performance assessment of level controllers [J].International Jour nal of Adaptive Control and Signal Processing, 2003,17:663-684.

