SHPB恒应变率加载试验技术研究

梁书锋， 武　宇， 刘殿书， 李晓璐， 张会歌

(中国矿业大学 力学与建筑工程学院，北京 100083)

0　引言

自1949年Kolsky提出分离式Hopkinson压杆以来[1]，这一试验技术得到了长足的发展并日趋完善[2-4]，成为研究材料在高应变率下力学行为的一项经典的测试技术，恒应变率加载对研究高应变率下材料的本构关系具有非常重要的意义，因此开展恒应变率试验技术方面的研究显得尤为重要.

在众多实现恒应变加载条件的技术中，脉冲整形技术早就进入研究者的视线，并形成了大量的研究成果.文献[5]提出脉冲整形器思想，通过在霍普金森扭杆冲击端粘贴薄片形整形片的方法，获得较为理想的试验效果.国内的徐明利、卢芳云等也从脉冲整形器角度对试样中的应力平衡进行了大量研究.这些研究表明，选择合适的整形器能够解决传统霍普金森压杆存在的应力不平衡问题，而且通过对不同材料不同厚度的整形器进行组合可以在一定程度上实现恒应变率加载[6-8].文献[9]将脉冲整形技术应用在霍普金森压杆上，提高和改善了岩石应力-应变曲线初始部分的分辨率和精度.文献[10]尝试通过改变子弹的几何形状来研究脆性材料的大尺寸霍普金森压杆冲击力学试验，研究表明，采用半正弦加载波形对研究脆性材料动态力学性能非常有利，这种加载波形能够有效地消除应力波在波导杆中的弥散，其平缓的上升沿有足够的时间保证脆性岩石试件建立应力平衡，并通过数值模拟及电算程序得到子弹的形状.李夕兵等[11-14]针对试样中应力不均匀、波形弥散等方面的问题，从改变撞击子弹的形状入手进行了深入的研究，研究得出双锥形子弹产生的半正弦加载波不仅消除了波形弥散效应，而且较长的上升沿时间为试样中建立应力均匀条件提供了充足的时间，进而得出半正弦波是岩石类材料冲击性能试验的合理加载波形.文献[15]认为利用波形整形可减小Hopkinson杆实验在撞击过程中产生的高频振荡以及实现试样在受载过程中的恒应变率加载，并介绍了波形整形技术在Hopkinson杆的动态压缩、拉伸、巴西圆盘、弯曲断裂等试验中需注意的问题.文献[16]基于试验和数值模拟方法，对脆性材料进行SHPB试验，结果表明，应用脆性材料的SHPB试验应考虑惯性引起的径向围压的影响.

上述研究表明，SHPB实现恒应变率加载主要通过添加整形器和改变子弹形状两种方法，但是添加整形器实现恒应变率加载在试验重复性方面有缺陷，而通过改变子弹形状来实现恒应变率加载则是可行的.因此笔者从改变子弹形状入手，通过数值模拟和试验验证的手段，研究SHPB恒应变率加载技术.

1　恒应变率加载实现的判据

“二波法”计算应变率，

(1)

式中：εr为杆中反射波的应变.若要实现恒应变率加载，式(1)中εr(t)应为常数，在理想状态下波形曲线中反射波形会出现如图1所示的平台段.

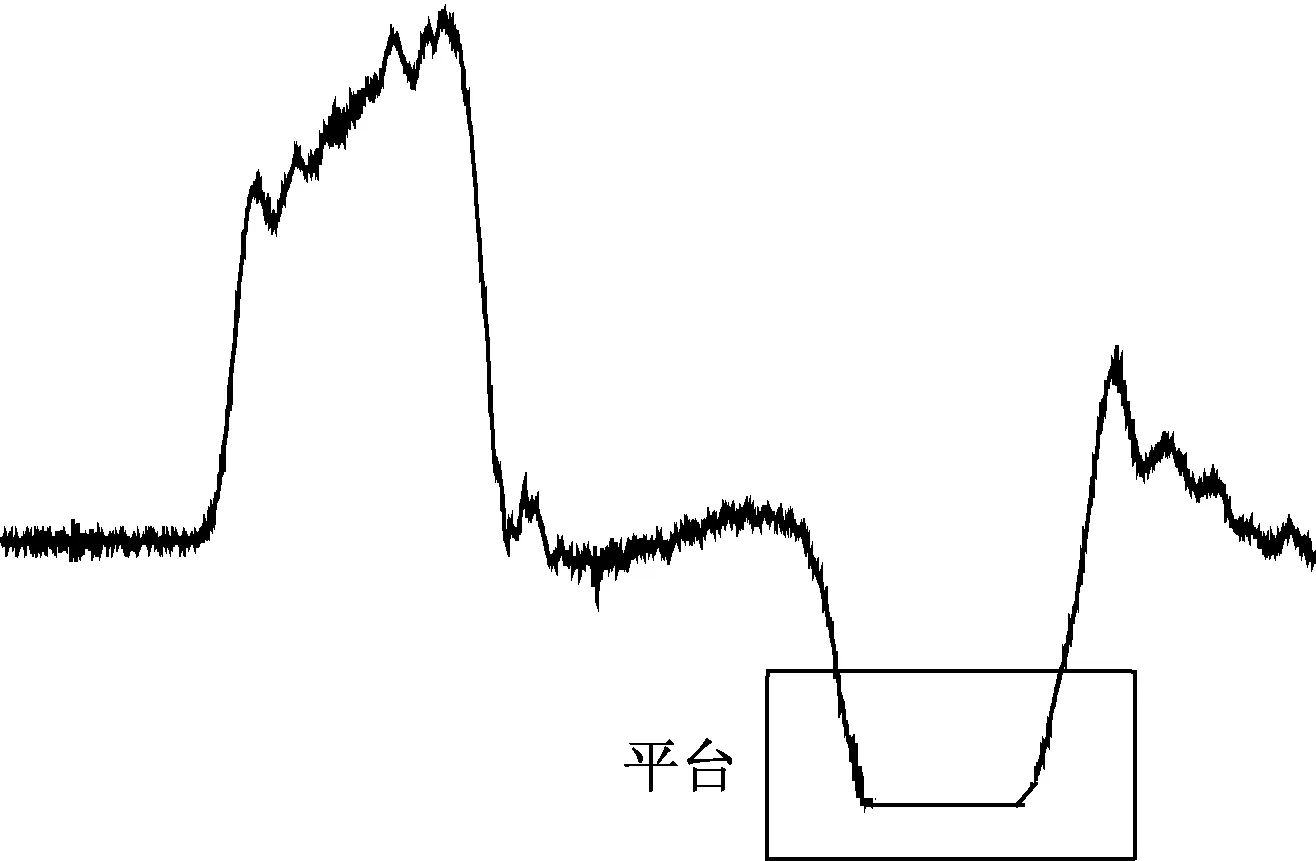
图1　反射波平台段示意图Fig.1　Schematic diagram of reflection wave platform period

笔者所在的课题组在Φ75 mm钢杆系统基础上做了关于异形子弹的相关试验研究，并得出了以下结论：①入射波持续时间由子弹的总长度决定，不会因冲击速度的变化而改变.变截面子弹能有效地改变入射波形，随着撞击端由等截面缩小为变截面，入射波应力峰值降低，上升区段趋于平缓，振荡现象减少，整体趋向钟形波.②在理想状态下采用柱锥形子弹应该存在平台段，平台段与入射波宽度的比值与柱段和子弹长度的比值大致相当，但当长度比值小于等于1/3平台段消失，柱锥形子弹只能在固定的时间脉冲内改变上升沿的形状.③子弹前后形状会对波形造成不同的影响，前端的形状改变上升沿，尾部的形状改变下降沿；前部锥长越长，波形越平缓，振荡现象也越少，但相应的峰值应力会下降.该项研究为笔者建立Φ50 mm霍普金森压杆恒应变率加载技术提供了思路与数据.

2　恒应变率加载的实现

笔者研究恒应变率是基于异形子弹方法开展的，采用从双试件处理方法演变而来的柱锥形子弹整形技术，在研究过程中发现这种柱锥形子弹需要满足两个基本原则.①锥形的小端面截面与大端面截面面积之比不能过小，因为如果锥前端界面直径过小入射波便不再是一维的，而且有可能在脉冲头部到达锥顶之前产生足够大的拉应力，最终导致锥顶部分断裂，因此在设计锥形杆的过程中应控制锥体大端面面积与小端面面积的比值,具体的比值将在下面研究中确定.②柱锥形子弹所产生的脉冲波上升沿持续时间应保持一定的长度以满足试件应力平衡要求.以下将对两个原则从理论、数值计算和试验方面进行讨论.

首先是子弹长度的选择，从笔者所用花岗岩试件的最大长度Ls=41 mm为例，其声速5 069 m/s，计算得出子弹长度L=243 mm.考虑到今后对其它种类岩石的适用性，将子弹长度值固定为400 mm，而柱锥子弹大端面直径设定为50 mm.柱锥形子弹所产生的脉冲波形是二级分阶段的加载波形，因此采用柱锥形子弹来实现恒应变率具备合理性.其设计应服从以下两个原则.

2.1　锥体两端面大小比例关系

图2为强间断波阵面传播图.

图2　强间断波阵面传播图Fig.2　Discontinuous wave front propagation graph

根据波阵面上的质量守恒定律，得出公式(2)：

(σ+-σ-)A0dt=ρ0A0dX(v+-v-).

(2)

经简化后可得：

[σ]=-ρ0c[v].

(3)

应力波在变截面杆中传播的过程中，应力波经过截面发生突然变化的界面时，将会发生反射和透射，如图3所示.

图3　变截面杆中波的反射与透射Fig.3　Reflection and transmission of variable cross-section wave

图3为变截面杆中波的传播反射.根据牛顿第三定律，A1、A2两个面上所受的力相等.于是有

A1(Δσ1+ΔσR)=A2(ΔσT).

(4)

根据连续条件，A1、A2面接触的地方反射透射后质点速度相等，则有

Δvt+ΔvR=ΔvT.

(5)

将式(3)带入式(5)可得

(6)

联立式(4)、(6)求解可得到：

(7)

(8)

(9)

当界面两侧波阻抗ρ0C0A相同时，应力波仅仅因截面的变化引起反射和透射，此时n=A1/A2.则ΔσT=TAΔσt.当应力波由杆的大截面传入小截面时，F=(1-n)/(1+n)小于零，此时杆中透射应力波大于入射应力波.锥形杆可近似看做是一系列面积发生变化的阶梯杆，当压缩脉冲从大端面向小端面传播时，每通过一个截面积变化的面时，透射波都会增强T=2/(1+n)倍，同时反射一个反方向的拉伸波，该拉伸波由小截面向大截面传播过程中将反射一个反方向的增强拉伸.如此反复，随着压缩脉冲向锥顶传播，脉冲头部压缩区的应力波幅值将越来越大.

为进一步验证以上结论，建立长度为400 mm的柱锥杆有限元模型进行数值计算，圆柱段暂定为100 mm，大小端面直径分别为50、35 mm.入射杆、透射杆长度都采用2 000 mm.计算时子弹的加载速度为5 m/s，计算完成后沿柱锥杆长度方向等距离提取单元的应力时程曲线，子弹模型及单元应力时程曲线如图4、图5所示.

图4　柱锥子弹有限元模型Fig.4　The model of cylinder cone bullet

图5　单元应力时程曲线Fig.5　Element stress time history curve

从图5可以得出，锥前端应力为锥后端应力值的2倍多，这与数例计算结果相近.如果锥前端界面直径过小就有可能在脉冲头部到达锥顶之前产生足够大的拉应力，最终导致锥顶部分断裂，因此在设计锥形杆的过程中应控制锥体大端面面积与小端面面积的比值.从另一个方面，当引入的锥形子弹小端面截面积较小时会造成波的弥散，不满足霍普金森压杆的一维假定.同时根据试验选用花岗岩屈服强度98～245 MPa，以及笔者拟选用锥杆材料7075铝镁合金屈服强度503 MPa，是花岗岩屈服强度的2.05倍，大小截面面积之比为4时，达到初始应力的1.84倍，因此确定直径比为2.由于数例采用阶梯杆近似计算，实际锥形杆中满足要求的直径比小于2.根据数值计算结果，大端面与小端面面积之比不小于4/9，即直径之比大于2/3.

2.2　加载波上升沿时间

传统的霍普金森压杆实验采用圆柱形子弹直接撞击加载，加载波形近似方波，上升前沿约为10～20 μs，对于金属类高阻抗材料，其弹性波速度一般在5 000 m/s左右，即使试件长度超过10 mm，也能在加载波的上升时间内达到应力平衡.对于低阻抗的岩石类材料，材料的波速可能很低，加之所要求的试件长度较长，因此所需达到应力平衡的时间大于20 μs.文献[17]的研究表明，加载波在试件中来回反射3～6次以上可以达到试件的应力平衡要求.对于岩石类材料，例如本研究中的花岗岩，平均波速为5 069 m/s，试件长度为40 mm，据此计算，t0为弹性波通过试件的时间，对于花岗岩t0=7.89 μs，所以第一段上升沿时间应不小于23.67～47.34 μs.

综上确立柱锥杆两原则：①子弹打击端面与入射杆受击端面直径比值不小于2/3；②入射波一段上升时间大于23.67～47.34 μs，以满足试件中应力平衡要求.按照此原则设计的子弹如图6所示.

实际使用中，在子弹上面夹套2个聚四氟乙烯环以保证子弹冲击过程中的稳定性.

图6　设计的柱锥子弹图Fig.6　The designed conical-cylindric bullet

3　恒应变率加载验证

3.1　数值计算验证

利用有限元数值分析来验证所设计的柱锥形子弹能够实现岩石类材料的恒应变率加载，数值分析选用描述混凝土本构模型的HJC进行计算.其本构模型参数如表1所示.

混凝土强度为30 MPa，子弹以10 m/s速度对混凝土进行冲击加载，获取波形如图7所示.

从图7可以看出，在端面形状A=50 mm，B=35 mm，锥长300 mm的子弹冲击下，试件的反射波形平台虽有震荡但总体呈现出直线形式，试样在试验过程中的应变率由入射杆中反射应力波的时间历程确定，也就是说，如果霍普金森压杆试验获得的反射波测试信号除去上升、下降沿外大部分保持平台状，即可认为试样冲击变形过程是在恒应变率条件下发生的，由此可以判定该形状的子弹实现了对试件的冲击恒应变率加载.

表1　混凝土HJC本构材料参数表

图7　混凝土Mat159在50-35-300子弹冲击下波形图(v=10 m/s)Fig.7　Impact waveform within concrete Mat159 under 50-35-300 bullet (v=10 m/s)

3.2　试验验证

利用设计的柱锥形子弹对花岗岩试件进行冲击，得出不同冲击速度下波形图，观察上述反射波平台是否出现，并将波形图与原圆柱形子弹不同速度冲击波形图进行对比.图8、图9为柱锥子弹不同速度冲击波形图.

图8　柱锥子弹不同速度冲击波形图Fig.8　Shock wave of different velocities in cylinder-cone bullet

图9　圆柱形子弹不同速度冲击波形Fig.9　Shock wave of different velocities in cylinder bullet

从图8～9可以看出，不同冲击速度下锥形杆获得的反射脉冲基本呈平台状(红色虚方框中).对于相同的试件，圆柱子弹不同冲击速度产生的反射脉冲形状为“v”字形.通过对比可以看出，笔者设计的柱锥形子弹改善了原圆柱子弹冲击反射波的形状，实现了反射波呈平台状，即实现了冲击恒应变率加载.需要说明的是，试验中所呈现的“平台段”并非本文图1所示绝对的平台，这是由于输入、输出杆存在的弯曲变形造成的[18].另外，从统计学的角度来看，在笔者所在教研室该类试验所获得的大量波形中，如图8中所示反射波平台状波形所出现的比例占到77.7%，因此认为恒应变率冲击试验达到良好水平，实现了恒应变率加载.

4　结论

(1)对传统SHPB试验系统、数据处理原则和大直径SHPB装置在岩石材料中应用的条件等方面进行了分析，由此确定本试验花岗岩的试件长径比为0.75～0.82；并得出实现恒应变率加载是解决大直径SHPB装置弥散效应、应力均匀等问题的有效手段.

(2)通过对SHPB试验入射波整形技术的分析研究，确定了从双试件法演变而来的柱锥形子弹是实现恒应变率加载的有效手段.利用应力波理论及数值计算建立了柱锥形子弹所应遵循的两个原则：①锥体小端面与大端面直径之比应大于2/3；②加载波上升沿时间应满足应力波在试件中传播3～6次时间.根据计算，笔者所采用的花岗岩上升沿时间应大于23.67～47.34 μs.

(3)运用数值计算手段对总长度400 mm柱锥子弹的不同形状参数进行数值分析，得出适合花岗岩最优柱锥子弹端面比，小端面直径与大端面直径比为0.7，该值大于2/3满足要求，据此确定大端面直径为50 mm，小端面直径为35 mm，并进一步对子弹不同锥长大小进行分析，结合理想弹塑体加载波形，确定最优的锥长为300 mm.

(4)从数值模拟和试验两个角度出发，通过与传统圆柱子弹加载波形对比，验证了所设计的柱锥形子弹实现了对花岗岩的恒应变率冲击加载.

参考文献：

[1]KOLSKY H.An investigation of the mechanical properties of materials at very high rates of loading[J]. Proceedings of the physical society of london, 2002, 62(11)：676-700.

[2]FOLLANSBEE P S,FRANTZ C.Wave propagation in the split hopkinson pressure bar [J]. Journal of engineering materials and technology,1983,105(1):61-66.

[3]GORHAM D A. A numerical method for the correction of dispersion in pressure bar signals[J]. Journal of physics E: scientific instrumentation,1983,16(6):477-479.

[4]GONG J C, MALVERN L E, JENKINS D A. Dispersion investigation in the split hopkinson pressure bar[J]. Journal of engineering materials and technology,1990,112(3):208-214.

[5]DUFFY J, CAMPBELL J D, HAWLEY R H. On the use of a torsional split hopkinson bar to study rate effects in 1100-0 aluminum[J].Journal of applied mechanics,1971, 38(1): 83-91.

[6]FREW D J,FORRESTAL MJ,CHEN W. Pulse shaping techniques for testing elastic-plastic materials with a split Hopkinson pressure bar[J].Experimental mechanics, 2005, 45(2):186-195.

[7]FREW D J,FRORRESTABL MJ,CHEN W.Pulse shaping techniques for testing brittle material with a split Hopkinson pressure bar[J].Experimental mechanics, 2002, 42(1): 93-106.

[8]卢芳云, W.Chen, D.J.Frew.软材料的SHPB实验设计[J].爆炸与冲击，2002,22(1):15-19.

[9]CHRISTENSEN R J, SWANSON S R, BROWN W S. Split-Hopkinson-bar tests on rocks under confining pressure[J].Experimental mechanics, 1972,33(8): 508-513.

[10] LOK T S, LI X B, LIU D, et al. Testing and response of large diameter brittle materials subjected to high strain rate[J]. Journal of materials in civil engineering,2002,14(3): 262-269.

[11] 李夕兵,刘德顺,古德生.消除岩石动态实验曲线振荡的有效途径[J].中南工业大学学报,1995, 26(4):457-460.

[12] 刘德顺,李夕兵,杨襄璧. 截面连续变化冲锤与杆撞击的特征线数值计算法[J].中南工业大学学报,1996, 27(5):591-595.

[13] 李夕兵, 刘德顺, 刘爱华. 冲击机械合理加载波形的形究[J].中南工业大学学报,1998, 29(2):116-119.

[14] 杨卫忠,王博. 基于细观损伤的岩石受压本构关系模型研究[J]. 郑州大学学报(工学版),2010,31(6):6-9.

[15] 果春焕,周培俊,陆子川,等. 波形整形技术在Hopkinson杆实验中的应用[J]. 爆炸与冲击,2015,35(6):881-887.

[16] 卢玉斌,武海军,赵隆茂. 脆性材料SHPB实验中实现近似恒应变率加载研究[J]. 西南科技大学学报,2013,28(3):50-56.

[17] RAVICHANDRAN G, SUBHASH G. Critical appraisal of limiting strain rates for compression testing of ceramics in a split hopkinson pressure bar[J]. Journal of American ceramic society,1994, 77: 263-267.

[18] 叶仁传, 天利, 沈超明. 霍普金森压杆(SHPB)实验波形震荡问题的影响与解决方法[J].科学技术与工程,2014,14(1)：1-4, 9.