矢量拉普拉斯算符简析
金 杰, 张瑞峰
(天津大学 1. 电气自动化与信息工程学院, 2. 微电子学院, 天津 300072)
0 引言
在“电磁场与电磁波”课程中,矢量拉普拉斯算符是一个不可回避的问题。其比较有代表性的出现计有三处,一是在关于矢量磁位泊松方程的推导中,二是在关于动态矢量位的达朗贝尔方程(又称非齐次波动方程)的推导过程中,三是在均匀无耗媒质无源区中关于电场强度和磁场强度波动方程的推导过程中[1,2]。在直角坐标系下,矢量拉普拉斯可以方便地转换成标量拉普拉斯,这一点非常关键,它为求解场的基本方程开辟了一个非常广阔的新方向:因为转化成了二阶偏微分方程的求解问题,存在大量的成熟计算方法以及商用软件可资利用,如分离变量法、有限差分法和有限元方法以及Ansys、CST和COMSOL Multiphysics等软件,可以说极大提高了人们的对于电磁场及波问题的求解能力。
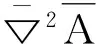
1 基本矢量拉普拉斯算符推导

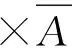
(1)
展开可以得到:
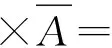
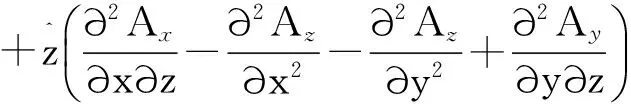
(2)
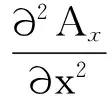
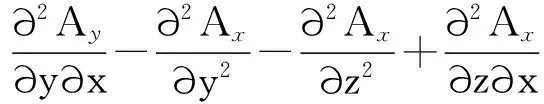
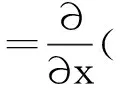
(3)
对于另外两个分量也如是操作,有
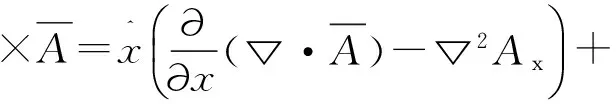
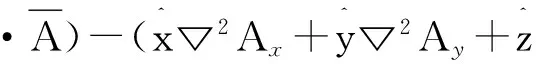

(4)
最终的结论是:
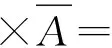
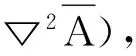
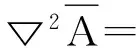
(5)
也可简述为矢拉等于梯散减双旋。
▽2Ax=-μ0Jx
▽2Ay=-μ0Jy
▽2Az=-μ0Jz
(6)
虽然式(5)是在直角坐标系推导得出的结论,但是完全可以应用到圆柱坐标和球坐标系。
2 圆柱坐标和球坐标系的推导
应用上文的式(5),即可推导出圆柱坐标系中的矢量拉普拉斯算符:
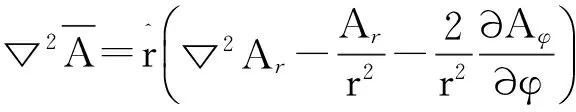
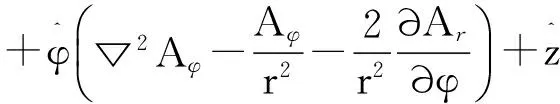
(7)
以及球坐标系中的矢量拉普拉斯算符
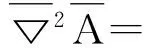
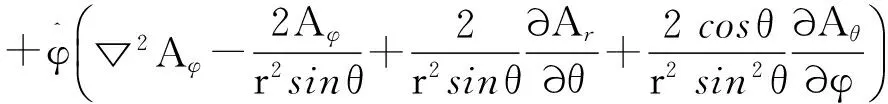
(8)
3 结语
本文总结归纳了矢量拉普拉斯算符在“电磁场和电磁波”课程中的应用之处及其重要意义。从直角坐标系出发,推导了具有普适意义的矢量拉普拉斯算符表达式,即矢拉等于梯散减双旋。以此为基础,又推导了圆柱坐标和球坐标下的矢量拉普拉算符的表达式。希望本文能对同行有些启发作用。
参考文献:
[1]谢处方,饶克谨. 电磁场与电磁波(第三版)[M].北京:高等教育出版社,1999年6月.
[2]毕德显,电磁场理论[M]. 北京:电子工业出版社,1985年2月.
[3]D.K.Cheng著,何业军,桂良启译. 电磁场与电磁波(第二版)[M]. 北京:清华大学出版社,2013年2月.
[4]P.Lorrain,D.R.Corson著,陈成钧译. 电磁场与电磁波[M]. 北京:人民教育出版社,1980年7月.
[5]E.M.Purcell著. Electricity and Magnetism(英文影印版)[M]. 北京:机械工业出版署,2014年6月.

