中国房价波动的金融资产价格效应
黄 文, 王 晔, 谢 雨 菲
(1.河海大学 商学院, 江苏 南京210098; 2.南京大学 商学院, 江苏 南京210093)
一、引 言
近此年一直作为国民经济中的基础性和先导性产业的房地产业与其他产业之间高度关联,是推动近年来我国经济增长的重要力量。房地产业的高速发展也推动了房价的迅速攀升。中国房地产网资料显示,从1998年我国住房货币化改革到2015年的近20年里,我国商品房的平均价格从刚刚突破每平米2000元涨到每平米7571元,涨幅高达279%。2016年以后,中国房地产市场百城住宅价格持续增长,2016年1~11月份累计上涨17.83%,较2015年全年扩大13.68个百分点,其中一、二线城市的累积涨幅分别高达22.95%和13.34%,而与此同时,多数三、四线城市面临“去库存”难题,全国市场区域分化态势延续。房地产的虚拟资产特性使得其价格与成本相脱离,并且具有很强的波动性。随着近几年货币信贷政策的收紧和各级政府房价调控政策的陆续出台,热点城市房价在经历大涨后更容易产生大幅波动。作为居民资产配置的重要组成部分以及商业银行发放贷款的主要抵押品,房价的波动会直接导致居民财富总量和货币供给的变动,进而引起社会生产、消费等实际领域的变化,同时对金融市场中金融资产的价格产生影响。
事实上,在房地产市场经历周期性波动的同时,我国的金融市场也在跌宕起伏中发展,房价和金融资产价格从运动轨迹来看表现出一定的相关性,房价波动会推高市场运行风险,助长或者挤压金融资产价格中原有的泡沫,并对金融体系的稳健运行带来隐患。为此,本文将从股票市场和债券市场着手,对我国房价波动的金融资产价格效应进行全面系统的研究。
二、文献综述
房价波动不仅会引起宏观经济指标的变动,还会对金融市场产生冲击。大量研究指出,房价波动与银行信贷规模存在紧密的关系,并且房价波动会借由信贷市场的“金融加速器效应”引起金融系统的不稳定。Gerlach和 Peng利用1982年到2001年香港的季度数据对银行贷款、房价之间的长期均衡和短期波动关系进行了实证分析,结论是香港地区房价波动会影响银行信贷的扩张[1]。Goodhart 和 Hofmann发现,信用扩张和房价波动存在双向影响关系,但房价对信贷的影响比信贷对房价的影响要大得多[2]。段忠东等运用多变量协整分析技术对我国房价影响银行信贷的效应进行实证检验,研究表明,房价和银行信贷之间在长期内存在互为因果关系,但是短期内房价波动对银行信贷发放的直接影响十分有限[3]。林江等利用VAR模型对深圳的商品房住宅市场进行了研究,发现深圳市商品住宅交易均价与金融信贷互为Granger因果关系[4]。
也有一些学者针对房价波动和金融资产价格的关系进行了研究,其中大部分是关于房地产市场和股票市场相关性的研究。Quan和Titman运用17个不同国家和地区14年间的数据进行检验,发现股价与商业房价有很强的相关性,但在亚洲,股票价格与房价的相关性会减弱[5]。Tse的研究表明香港房价和股价存在协整关系,并且使用VAR模型和脉冲响应分析证明了香港房价波动是导致股价变动的决定性因素,房价和股价负相关[6]。Yang利用协整检验表明,瑞典的房价、股票价格和国债价格存在一个长期的均衡关系,且这3个变量有着类似的运动轨迹[7]。沈悦和卢文兵利用协整分析和VAR模型对我国股票市场与房地产市场的关系进行实证研究,结果表明房价上涨对股票价格上升有显著影响,房价的上升与股票价格的上升存在两季左右的间隔,且两者呈现出螺旋式变化的趋势[8]。巴曙松等利用变点检验、线性和非线性Granger因果检验的计量方法研究了房地产市场化改革完成后中国股票市场和房地产市场的关系,发现股市是房市的线性Granger先导,而房市在一定程度上对股市有滞后的非线性Granger的引导作用[9]。彭兴庭选取了GARCH模型进行研究,认为房市和股市之间的波动存在溢出效应,而且是单向的,即房地产市场的波动将引起股票市场的波动[10]。林众和林相森同样利用了VAR模型,基于预期效应、财富效应与替代效应的传递机制来研究中国房地产市场与股票市场之间的相关性,其研究结果表明,在长期内房地产市场与股票市场不存在稳定关系;在短期内,房地产市场对股票市场的替代效应引起的负效应起主导作用且较显著[11]。
通过上述文献回顾可以发现,国内外学者对于房价波动效应的研究主要集中在房价波动对金融市场的影响。我国学者对这一领域的研究起步比较晚,其中,关于房价波动对金融资产价格的影响,大多探讨的是房地产市场和股票市场的关联性,较少聚焦于债券价格受房价波动的影响。从研究方法来看,现有文献中用的较多的方法是协整检验和Granger因果检验,这些方法虽经典但也存在一些不足。基于此,本文在构建理论框架的基础上,采用时变参数向量自回归(TVP-VAR)模型,研究样本期内房价波动对股票和债券这两种金融资产价格的时变效应。
三、模型构建与估计方法
在过去的10多年里,我国房地产市场和金融市场都经历了快速成长,各时期的宏观经济变量和政策形势也不尽相同。因此,分析房价波动对我国金融资产价格的影响,不能采用固定参数模型来研究。为了充分反映我国经济结构的动态变化,本文通过构建时变参数向量自回归(TVP-VAR)模型,并选用股票和债券作为金融资产的代表,试图全面揭示房价波动对金融资产价格的动态影响。
1.三变量TVP-VAR模型构建
首先,构造一个基础的结构向量自回归(SVAR)模型:
Ayt=F1yt-1+…+Fsyt-s+ut,t=s+1,…,n
(1)

yt=B1yt-1+…+Bsyt-s+A-1∑εt,εt~N(0,I3)
(2)
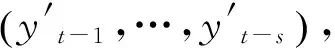
yt=Xtβ+A-1∑εt
(3)
为探究房价波动对金融资产价格的时变影响,将模型(3)中所有的参数加入时变特征,便得到了如下的时变参数向量自回归(TVP-VAR)模型:
(4)

2.模型估计方法

基于上述假设,本文使用贝叶斯估计以及马尔科夫蒙特卡罗(MCMC)算法对所构建的TVP-VAR模型进行估计。
四、实证检验
1.样本选择与数据说明
房价以商品房月度销售单价来表示,缺失的一月份数值用线性插值法计算补足。金融资产价格以股票价格和债券价格来代替,其中,本文采用上证A股指数收盘价作为我国A股市场行情的衡量指标,选取中债综合指数中的总净价指数反映债券市场总体情况。由于上证A股指数和中债综合指数的原始数据是日度数据,本文以月内日度数据的算术平均值反映该月的股票价格和债券价格的总体变化情况。由于中债综合指数的起始日期为2002年1月,考虑到数据的可得性,本文的样本期间始于此。另外,本文写作时能够获得的完整数据的截止月份为2016年11月,因此,本文的样本期间为2002年1月~2016年11月,共179组样本数据。将上述月度价格指标用Census-12方法进行季节调整,得到房价、股价和债券价格经过季节调整后的序列,分别记为HOUSE、STOCK和BOND。
房价HOUSE、股价STOCK和债券价格BOND这3个价格序列的单位根检验结果见表1。由表1可知,房价序列在1%的显著性水平上拒绝了序列含有单位根的假设,因此,该序列是平稳的;股票价格序列在经PP检验后表明不平稳,且ADF检验结果显示在5%的显著性水平上不能拒绝序列含有单位根的原假设,因此,可以认为该序列是不平稳的;对于债券价格序列的ADF检验和PP检验结果均表明不能拒绝该序列存在单位根的假设,因此,该序列也是不平稳的。

表1 价格序列单位根检验结果
注:ADF检验形式(c,t,n)中的c,t,n分别代表常数项、趋势项和滞后阶数,PP检验形式(c,t,b)中的c,t,b分别代表常数项、趋势项和带宽。
为了避免时间序列不平稳造成“伪回归”问题,同时减弱异方差的影响,本文将上述价格序列均作对数差分处理,从而得到上述房价、股票价格和债券价格的收益率序列,分别记为house、stock、bond。这3个收益率序列的单位根检验结果如表2。ADF检验和PP检验结果均表明,房价收益率、股价收益率和债券价格收益率都满足平稳性要求,可以进行TVP-VAR模型估计。

表2 资产价格收益率序列单位根检验结果
注:ADF检验形式(c,t,n)中的c,t,n分别代表常数项、趋势项和滞后阶数,PP检验形式(c,t,b)中的c,t,b分别代表常数项、趋势项和带宽。
2.TVP-VAR模型参数估计
运用TVP-VAR模型进行估计之前,首先要选择模型中的滞后阶数。为此,本文先把房价收益率House、股价收益率Stock和债券价格收益率Bond代入传统的VAR模型,滞后阶数分别选取0~4阶,得到结果如表3。由表3可知,根据LR准则、FPE准则和AIC准则,最佳滞后阶数应为4阶,而根据HQIC准则和SBIC准则,最佳滞后阶数应为1阶。为简化模型,同时尽可能不丧失自由度,本文在进行TVP-VAR估计时选取的滞后阶数为1阶。

表3 滞后阶数选择
用MCMC算法连续抽样10 000次,舍弃预烧(burn-in)阶段的前1000次抽样,得到各参数的后验均值、标准差、95%的置信区间、收敛诊断值和无效因子,如表4所示。

表4 MCMC算法估计结果
表4显示参数的后验均值都在95%的置信区间内,因此,模型的估计结果是可信的。CD统计量均小于5%显著性水平下的临界值1.96,说明无法拒绝后验分布收敛于0的零假设。无效因子最大为85.45,表明我们共得到了10000÷85.45≈117个不相关样本,这足以满足后验推断的要求。
图1从上到下分别是样本的自相关图、样本路径以及被选参数的后验密度函数。自相关图表明在舍弃了最初的1000次样本后,样本的自相关系数迅速下降并且在0附近波动,可以判断样本基本不存在自相关关系。另外,10 000次有效样本的样本路径比较平稳,路径显示参数具有显著的波动聚类现象。上述结果表明,MCMC算法有效地模拟了参数的分布状况。
3.房价波动对金融资产价格的同期效应分析

如图2所示,房价波动对股票价格和债券价格的同期效应均呈现出时变特征。2005年5月之前,房价收益率和股价收益率、房价收益率和债券价格收益率的同期相关系数均小于0,表明在此期间,房价上升抑制了同期金融资产价格的上涨。究其原因:2005年之前,我国的股票市场和债券市场长期处于“熊市”的阴霾中。一方面,股权分置改革尚未进行,制度性缺陷束缚着股票市场发挥其应有的资源配置、投资理财功能;另一方面,债券市场交易品种较少,债券远期交易、短期融资券等品种尚未推出,信用债市场以企业债为主,发改委对其采取严格的审批制度限制了其规模的增长,商业银行进入公司债券的大门也还未打开,债券市场增长比较缓慢;而房地产市场自1998年货币化制度改革以来,在土地和建材价格上涨、购房需求旺盛、以及投资者炒作等因素的影响下热度高涨。在此背景下,投资者竞相追逐高收益的房地产,将资金撤离收益率较低的股票和债券市场,导致股票和债券收益率进一步走低,从而形成了房价波动对金融资产价格的“替代效应”,在图2中,即表现为两者同期的负相关关系。此外,注意到0轴一直被包括在95%的置信区间内,这说明在5%的显著性水平上,不能拒绝同期关联系数为0的原假设,这说明在2005年5月之前房价波动对金融资产价格的同期影响不显著。
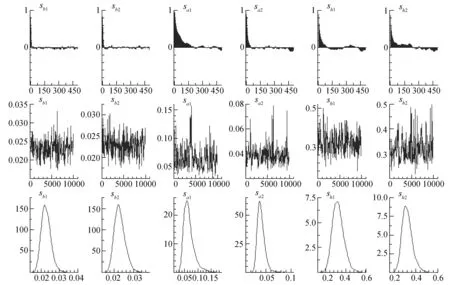
图1 样本自相关图(上)、样本路径(中)和密度函数(下)
2005年5月之后,房地产市场和股票市场、房地产市场和债券市场的同期影响情况发生了分化。从图2(a)关联系数后验均值的走势可以看到,房价收益率对股价收益率的同期影响在2005年5月之后由负向变为正向,且关联系数的数值基本处于稳步上升的态势,表明在此期间房价的上涨会推升同时期的股票价格;2013年后,后验均值一直保持在0.35附近,表明2013年后,房地产市场对股票市场的同期影响力度趋于稳定。结合股票市场的发展情况,2005年4月29日晚,股权分置改革的试点启动,自此,我国证券市场制度才开始逐渐完善,证券市场真实的供求关系和定价机制才得以发挥作用。从此A股市场开始步入上升通道,市场活跃度持续增加,股票逐渐成为了投资者寻求资金保值增值的重要金融工具。在这一阶段,房价波动对股票价格的同期影响可以用“财富效应”、“抵押品效应”和“开发企业效应”等来解释。首先,房价上涨使得房屋所有者总体财富增加,人们在变得“富有”时往往更加有能力进行金融资产投资;由于股改后,股票在投资者资产组合中的地位上升,根据“财富效应”,投资者在自身财富增加时会加大对股票市场的投资,从而促进了股票收益率的提升;其次,房价上涨使得房地产抵押贷款的资产质量提升,促进了银行的信贷投放,市场中流通货币增加使得资金成本下降,由于股改促使了我国股票市场的定价机制向市场化方向转变,股价对资金成本变动的敏感度提升,因此,2005年5月后,房价上升对股价的推动作用也更加能够通过“抵押品效应”得以实现;最后,在定价机制完善的金融市场中,股市应扮演着宏观经济晴雨表的角色,股改使得A股市场流动性有所提升,有助于股价变动反映实体经济波动,从而强化房价波动对股票市场的“开发企业效应”,即房价上升,房地产开发企业及其上下游产业的生产经营能力提高,使得房价与股价表现出正相关性。

图2 房价波动对股票价格和债券价格的同期影响注:图中实线为关联系数的后验均值,两条虚线之间为95%的置信区间。
虽然2005年5月之后房价收益率和股票价格收益率的同期关联为正,但是从置信区间来看,同期关联系数只有在2009年初至2013年上半年末这段时期内能够在5%的水平上保持显著。2009年下半年初至2013年上半年末正好处于A股市场两次暴涨暴跌时期之间。在A股市场,股市的大起大落常常伴随着投资者的非理性情绪以及股市政策的频繁变动,因此,股市大幅震荡期间股价的波动会脱离其原本的规律,股价受市场情绪左右,使得房价波动对其影响大大减弱。而2009年上半年初至2013年上半年末,股市总体相对稳定,这有利于股价反映经济基本面变动,在“开发企业效应”等作用下,房地产市场和股票市场的关联性更为显著。
结合图2(b)可知,2005年5月至2016年11月,房价收益率对债券价格收益率的同期关联系数时正时负,围绕着0轴上下小幅波动;到2012年3月之后才一直保持在0轴以上,且波动上升,最终稳定在0.1的水平上。图2(b)反映出以下3点:第一,2012年3月之前,房价波动对债券价格收益率的影响方向不明晰,房地产对债券的“替代效应”与“财富效应”等效应不相上下、轮流占优;2012年3月之后,房价上涨或下跌会引起债券价格的同向变动,这说明该时期“财富效应”“抵押效应”比较突出。第二,房价收益率和债券价格收益率的同期关联系数的绝对数最大仅为0.1,小于房价收益率和股价收益率的同期关联系数绝对数的最大值0.35,说明相对于股票市场,房价波动对债券市场的同期影响比较微弱。第三,在整个样本期间,房价收益率对债券市场收益率的同期影响系数95%的置信区间都涵盖了0值,即房市对债市的同期影响不显著。
回顾我国债券市场变迁史,2005年,短期融资券问世、商业银行投资企业债券的限制被打破以及信贷资产证券化试点开启都使得一级市场发行品种不断丰富,发行主体和参与主体显著增加,从而市场认购踊跃度增加、需求提升。随着债券市场在投资者资产配置中的比重增加,公司信用债在社会融资结构中占比上升,房价波动更容易通过“财富效应”和“抵押品效应”渠道影响债券价格。因此,在2005年后,房价对债券价格的影响来源于两股力量的角逐,一是资金的逐利性产生的“替代效应”致使两者反向运用,二是“财富效应”和“抵押品效应”致使两者同向运动,两股力量相互制衡,造成楼市波动对债市的冲击不甚明朗。2012年后,中小企业私募债的推出、国债期货的重启、资产证券化进程的加快等举措,都推动了债券市场进一步发展,债市与宏观经济的联系愈发密切,而房地产市场的发展又深刻影响着我国的宏观经济走势,因此,债市和楼市也日益表现出同向关联。尽管如此,我国债券市场尚且存在一些结构性问题。一方面,目前我国的债券市场以政府、金融机构和公有部门为主导,其对非金融私人部门企业提供服务的功能还比较欠缺,这使得债券市场与实体经济存在一定程度的脱节;另一方面,债券市场发行和流通环节的分割性、交易所市场和银行间市场的分割性、机构投资者和个人投资者的分割性使得债券定价机制不合理,市场收益率曲线无法充分反映供求关系。这些问题使得相对于股票市场而言,房价波动对债市收益率同期影响呈现并不十分显著的特点。
4.房价波动对金融资产价格的滞后冲击
为了全面考察我国房价波动对金融资产价格变动的动态效应,本文分别设定超前1期、3期、6期、9期(即超前1个月、1个季度、半年、3个季度),分析模型系统对外生冲击的响应。图3、图4分别描述了以股票、债券为代表的金融资产价格面临来自超前1期、3期、6期、9期房价收益率的一个单位标准差的正向冲击的脉冲响应图。

图3 股价对于正的房价冲击的响应
图3刻画了房价波动冲击对1个月、1个季度、半年、3个季度后的股票价格收益率产生的影响,波动的脉冲相应图很直观地显示了这种影响的时变性。脉冲响应结果传递出以下4点信息:第一,房价波动会对后一季度内的股票市场持续产生影响,且间隔一季度的影响程度约为间隔一个月的影响程度的1/2,而当间隔时间为半年以上时,股票市场基本不再受之前房地产市场波动的影响。第二,2002年2月到2005年5月、2009年2月到2016年11月这两段时间内,图3中脉冲响应值的符号与图2(a)中同期关联系数的符号基本一致,即2005年5月之前,同期关联和滞后冲击都表现为房价收益率和股价收益率的反向关联,房价波动主要通过“替代效应”作用于当期及滞后期的股票市场;而2009年2月之后的同期关联系数大于0,滞后冲击也总体显示出房价收益率和股价收益率的正向关联,房价波动主要通过“财富效应”、“抵押效应”和“开发企业效应”作用于当期及后期的股票市场,表现出楼市和股市共进退。第三,2005年5月至2009年2月期间,虽然图2(a)中房价收益率和股价收益率在“财富效应”等机制下表现为同期的正相关,但是图3中脉冲响应曲线几乎都处于0轴以下的区域,这说明,这段时间内房价波动对股价的“替代效应”在滞后期发挥了主要的作用。第四,2014年后,房价波动对股市的滞后影响稳定在一个相对较高的水平,考虑到该时期房价收益率和股价收益率同期也为正相关关系,可以判断,目前我国楼市对股市的同向促进作用比较稳定。
图4描绘的是房价波动冲击对超前1个月、1个季度、半年、3个季度后的债券价格收益率产生的影响,从图形的波动程度来看,冲击到响应的时间间隔越短,响应值的时变性越强,这与图3类似。而比较图3和图4中响应值的变动范围可以发现,在房价波动的冲击下,债券价格收益率的响应程度要比同时期股票价格收益率的响应程度小得多,这与同期关联效应中的结论一致。从图4的脉冲响应结果可知:第一,房价波动会对后一季度内的债券市场持续产生影响,且间隔一季度的影响程度约为间隔一个月的影响程度的1/3,表明相对于股票市场,房价波动对债市的滞后效应消失得更快,而当间隔时间为半年以上时,房地产市场波动对债券市场影响十分微弱。第二,在整个样本期间,图4中的脉冲响应曲线与图2(b)中同期关联系数的变动模式相同,即2005年3、4月之前,同期关联和滞后冲击都表现为房价收益率和债券价格收益率的反向关联,房价波动影响当期及滞后期债券市场的渠道主要是“替代效应”;2005年5月至2012年初,房价波动对当期及滞后期债券价格收益率的响应方向都不稳定;2012年后,同期关联和滞后冲击结果又同时表现为房价收益率对债券价格收益率的同向促进作用,这说明“财富效应”和“抵押品效应”等在该时期一直处于上风。第三,2014年后,债市对房价波动的滞后响应也趋于稳定,但从数值来看,不足股市滞后响应程度的一半,这也与债券市场分割、定价机制不完善有关。

图4 债券价格对于正的房价冲击的响应
五、研究结论与政策建议
本文利用2002年1月至2016年11月的月度数据,通过建立TVP-VAR模型,实证检验了我国房地产市场波动对以股票和债券为代表的金融资产价格的同期和滞后效应。本文的主要结论如下:
(1)就同期效应而言,房价波动对金融资产价格的同期影响呈现出时变性。2005年5月之前,房价上升抑制了同期金融资产价格上涨。2005年5月之后,随着股票市场和债券市场市场化程度的提升,房价上升对金融资产价格由抑制作用逐渐转变为促进作用。房价波动对股价的同期影响仅在2009年上半年初至2013年上半年末股市相对平稳的这段时间上显著,股市的暴涨暴跌会大大削弱房价波动对股票价格影响的显著性。同时,我国房价波动对债券市场的同期影响程度不如其对股票市场的同期影响。
(2)就滞后效应而言,房价波动对金融资产价格的影响具有持续性,可维持一个季度的时间,滞后效应的时变性随着间隔时间的增加而减小;相对于股票市场,房价波动对债券市场的滞后影响更小、消失得更快。2009年2月之前,房价上升会抑制滞后期股票价格的上涨;2009年2月以来,楼市对滞后期的股市有同向促进作用。2005年3月之前,房价上升抑制滞后期债券价格的上涨;2012年后,房价波动对滞后期债券价格保持同向促进作用;其余时间段上,房价波动对债券价格的冲击方向不明朗。
为减少房地产市场对金融市场的冲击,防止金融风险在房市、股市、债市累积和传递,保障国民经济平稳运行,本文提出如下政策建议:
首先,建立房地产调控政策的压力测试。监管部门在对房地产市场进行调控时,要考虑相关政策引起的金融资产价格的波动。在出台房地产调控政策之前,应建立模型并仔细考虑不同的购房首付比例或房贷利率对商业银行等金融机构、房地产及其他相关行业的影响范围和影响力度,基于此,分析在该情形下相应版块股票和债券价格可能的变动方向和范围,并据此制定应对金融市场波动的策略和方法。
其次,抑制房地产市场价格上涨,以实现房价平稳着陆。由于不同的经济金融环境中,房地产市场波动对金融资产价格的作用方向和力度不尽相同,为避免房价上涨或下跌幅度过大引发金融市场风险,当务之急还是应采取措施逐步收窄房价上涨幅度,抑制房地产泡沫的膨胀,保障房地产市场的平稳运行。
最后,完善股市和债市的基础制度建设,预防和控制金融资产价格大幅震荡。为防止金融资产价格异常波动,应围绕对投资者利益严密保护的原则,进一步完善股市和债市的基础制度建设。对于股票市场,应强化市场监管,严厉打击非法操纵市场的内幕交易行为,同时严格把控上市公司质量,杜绝虚假资本运作;对于债券市场,采取有效途径化解债券市场分割的局面,健全国内信用评级机制和市场化违约机制,以构建市场化、法制化、高效率、严监管的资本市场体系。
参考文献:
[1] GERLACH S,PENG W. Bank lending and property prices in Hong Kong[J]. Ssrn Electronic Journal,2004,29(2):461-481.
[2] GOODHART C,HOFMANN B. House Prices and the Macroeconomy:Implications for Banking and Price Stability[M]. New York:Oxford University Press,2006:132-144.
[3] 段忠东,曾令华,黄泽先,等. 房地产价格波动与银行信贷增长的实证研究[J]. 金融论坛,2007,12(2):40-45.
[4] 林江,徐世长,黄建新. 适应性预期、金融加速器效应与房价波动——以深圳为例[J]. 现代财经-天津财经大学学报,2015(1):22-31.
[5] QUAN D C,TITMAN S. Do real estate prices and stock prices move together? an international analysis[J]. Real Estate Economics,1999,27(2):183-207.
[6] TSE R Y C. Impact of property prices on stock prices in Hongkong[J]. Review of Pacific Basin Financial Markets & Policies,2001,4(1):29-43.
[7] YANG Z. Co-integration of housing prices and property stock prices:evidence from the Swedish market[J]. Journal of Property Research,2005,22(1):1-17.
[8] 沈悦,卢文兵. 中国股票价格与房地产价格关联性研究[J]. 当代经济科学,2008,30(4):87-92.
[9] 巴曙松,覃川桃,朱元倩. 中国股票市场与房地产市场的联动关系[J]. 系统工程,2009(9):16-21.
[10] 彭兴庭. 我国房地产市场与股票市场的波动相关性研究[J]. 北京理工大学学报(社会科学版),2011,13(5):39-43.
[11] 林众,林相森. 中国房地产市场与股票市场相关性的实证研究[J]. 统计与决策,2013(12):133-136.
[12] NAKAJIMA J. Time-varying Parameter VAR Model with Stochastic Volatility:An Overview of Methodology and Empirical Applications[R]. Institute for Monetary and Economic Studies,Bank of Japan,2011.

