基于改进型LMBP神经网络方法对蓄电池荷电状态的预测

王筱璇，侯冠军，孙思豪

（内蒙古电力（集团）有限责任公司锡林郭勒超高压供电局，内蒙古 锡林浩特 026000）

0 引言

为了保障变电站中直流电源铅酸蓄电池可以正常工作，需要预测蓄电池的荷电状态（SOC）。到现在为止，预测蓄电池 SOC 的方法有很多种。文献[1]比较了卡尔曼滤波法、人工神经网络法、动态逼近法这几种方法的优缺点：线性模型法中假设条件多，与实际情形有较大差别；卡尔曼滤波法计算复杂，对人员能力要求高；动态逼近法的精度性差；相比较下，神经网络具有快速、方便、较高精度的优点。文献 [2]提出一种变步长的 LMBP 神经网络计算方法，提高了 LMBP 神经网络算法的收敛速度，同时也提高了收敛性。文献 [3]讨论了锂离子动力电池的充放电特性，并建立基于标准 LMBP算法的电池 SOH 估算模型，但文章是以锂离子动力电池作为研究对象，并不适于变电站用铅酸蓄电池。文献 [4]讨论了蓄电池在充放电过程中特征参数的性质，同时通过 BP 神经网络对 SOC 进行估算，但采用 BP 算法收敛速度慢，隐含层层数与神经元数目不明确。

由于 SOC 可作为电池充放电控制和电池均衡的重要依据，当对变电站蓄电池组的单体 SOC 估算不准确时，会造成蓄电池组不均衡，损害蓄电池本身，减少蓄电池寿命。综上所述，为了保障蓄电池在变电站中可以正常运行，笔者采用改进型LMBP 神经网络算法估算电池的 SOC，可以提高估算的精度，延长电池寿命。

1 充放电模型的建立

目前，铅酸蓄电池模型一般可划为电化学与等效电路 2 种，后者更多应用在工程领域。在等效电路模型中，可以选择电流、温度等因素作为输入，以端电压、荷电状态等作为输出。等效模型主要有阻容和内阻模型，二者都可以模拟铅酸蓄电池的动稳态特性。由于阻容模型的结构简单，更易获得参数，具有较强的直观性，能够比较准确地反映蓄电池特性，因此笔者选取阻容模型作为电池的数学模型。图 1 所示数学模型中：E0为理想电压源；Rr为极化内阻；Cr为电容；Ub为端电压；R0为正负极板与电解液之间的非线性接触电阻。Rr与Cr组成的阻容电路影响了铅酸蓄电池工作变化时的过程。实际应用中将该过渡过程视为一个常量[4]。电池的充放电数学模型的数学关系式为：

图1 电池的充放电数学模型

2 改进型 LMBP 神经网络模型

2.1 改进型 LMBP 算法

LMBP 是基于 Levenberg-Marquardt 最优化方法的 BP 算法，因此收敛速度和收敛性有很大提升。本文中，笔者采用改进型 LMBP 算法，对一般的 LMBP 算法有所改进。LMBP 算法利用近似Hessian 矩阵的修正公式为

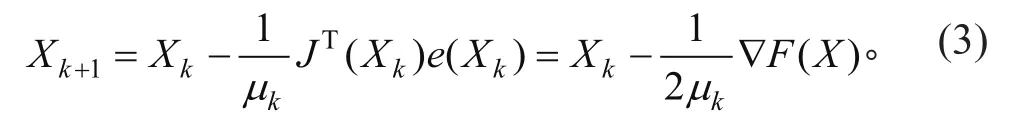
式中：Xk、Xk+1为列向量；F(X) 为误差平方和函数；F(X) 为F(X) 的梯度；J为 Jacobian 矩阵；e(Xk) 为误差函数；μk为增加的微小增量。当μk增加时，LMBP 算法接近梯度下降法，此时式（3）变为

若将式（4）变量改为ΔXk， 即

那么可得简化式

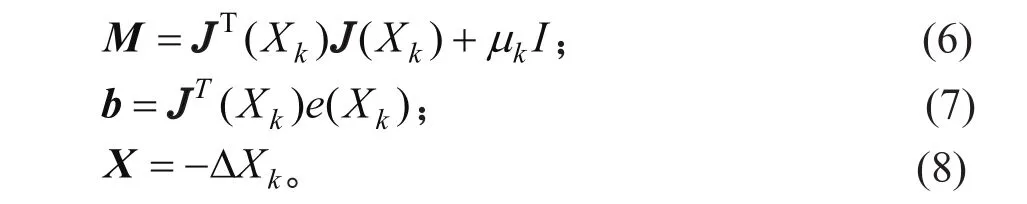
则式（5）变为

式中：M为n×n的逆阵；b为n×1 的向量；X为n×1 的向量。

一般的 LMBP 算法要计算矩阵M的逆阵，但是求逆操作相当费时。因此，将式（9）变形，把式子转化为线性方程组求解的问题，让等式（9）两边同时左乘矩阵M[5]，得

这样变形后，只需解出式（10），而且M是对称的正定矩阵，能够矩阵分解，所以提高了计算时间。

在一般的 LMBP 算法中，μk是非常重要的调整变量，但在计算中随着μk值的变大会出现 “小步长”的问题，一次迭代循环需要循环多次，致使运算效率低且耗费时间。而且，μk越大，“小步长”的现象越严重。为了解决“小步长”的问题，提出一种了固定的θ值表示变步长方式，使步进因子θ可变。变步长公式定义为

则μ值经调整策略，被改为

式中：θ' 为可变步进因子；k为进入此步小循环的次数。

文献 [2]的仿真实验验证了μk一般取 0.001，θ取 4 时结果较好。本文中，将式（10）与式（12）同时运用到一般的 LMBP 算法，使算法得以改进。

2.2 LMBP 神经网络模型的建立

模型的主要参数有E0、R0和Rr。在蓄电池正常工作过程中，环境温度、循环次数和 SOC 都可以影响模型参数，从而使参数发生变化，其中对模型影响最大的因素是 SOC。所以，建立铅酸蓄电池模型时，为了排除环境温度与循环次数对参数的影响，保持环境温度为 25 ℃，循环次数在 15～30 次的条件下，使 SOC 成为唯一对蓄电池参数有影响的因素。设蓄电池 SOC 的参数值为ζSOC，建立蓄电池E0、R0、Rr与 SOC 的数学关系。理想电压源E0与 SOC 的数学关系为

非线性接触电阻R0与 SOC 的单参数数学关系为

放电时蓄电池极化内阻Rr在放电情况下，与 SOC的数学关系为

2.3 神经网络结构设计

LMBP 神经网络结构为输入层、隐含层和输出层。根据 Kolmgoerov 定理，3 层的前馈网络有对任意精度连续函数逼近的能力。神经网络模型结构如图 2 所示[6]。

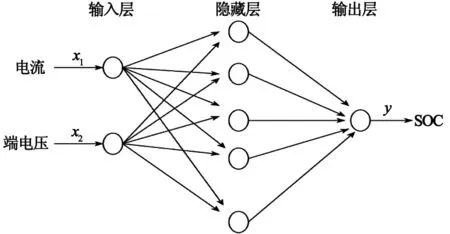
图2 神经网络模型结构

在本文中，设计输入层节点个数为 2，输入矢量为 [x1,x2]，其中x1为蓄电池的充放电电流I，x2为端电压U[7]。输入层在接收传输的I和U的同时也将数值量转换为模糊量，完成数据模糊化。模型输出层节点个数为 1，输出矢量为蓄电池荷电状态。输出层将隐含层输出的模糊量转化为蓄电池SOC。隐含层则按照模糊控制规则对输入层的模糊量进行判断，完成模糊推理过程。

2.4 网络训练数据与数据归一化处理

本文中，以额定电压 2 V、容量 100 Ah 的GFM-100 型铅酸蓄电池作为研究对象，采用蓄电池充放电综合测试系统对电池进行不同倍率的放电实验。此电池正常工作的充放电倍率范围是 0.2C～1C，所以将充放电倍率在该区间的实验数据作为训练样本，用电流积分法计算 SOC 的值[8]。

由于神经网络模型中，输入层为端电压U和电流I，这 2 个参数变化较大，量纲不同，若不处理数据，严重影响训练速度与输出权值，因此采用数据归一化消除影响，所用线性转换函数为

式中：X0为线性处理后的样本数据；Xi为原始样本数据；Xmax和Xmin分别为样本数据的最大值和最小值。

3 仿真结果分析

以 Matlab 仿真软件为平台，结合放电模型与改进型 LMBP 神经网络对铅酸蓄电池进行荷电状态的准确预算。为验证改进型 LMBP 算法的精确性与收敛性，用改进型 LMBP 神经网络模型的预测值和标准 LMBP 神经网络模型的预测值与 SOC 实际值作对比。在 25 ℃，放电倍率分别为 0.7C和 0.3C的条件下，对电池进行放电实验[9]。

从图 3、图 5 看出，放电前期，改进型 LMBP 和一般型 LMBP 模型预测值的与实际值相差较大；在放电后期，2 种算法模型的预测值逐渐接近实际值。图 3 中在 40 s 后，图 5 中在 100 s 后，改进型 LMBP算法模型估计值基本与实际值一致；图 3 中在 54 s后，图 5 中在 160 s 后，一般型 LMBP 算法模型估计值才与实际值一致：可以得出，改进型 LMBP 算法模型的计算速度要高于一般型 LMBP 算法模型的。图 4、图 6 为 2 种放电倍率下，改进型与一般型模型的绝对估算误差对比图。通过对比得出：放电初期，2 种模型的误差都大，后期误差逐渐减小，且改进型模型的预测误差要小于一般模型预测误差[10]。

在放电前期出现的 2 种现象的原因是，蓄电池放电前期电压变化慢，造成 SOC 估算困难，放电后期电压变化速度加快，有利于估算电池 SOC值。由图 3～6中的曲线走势比较得出，改进型LMBP 算法模型的估算精度要高于标准型 LMBP 算法模型的估算精度。

图3 0.7C 放电倍率下 SOC 估计值和实际值的对比

图4 0.7C 放电倍率下 SOC 绝对估算误差对比

图5 0.3C 放电倍率下 SOC 估计值和实际值的对比

图6 0.3C 放电倍率下 SOC 绝对估算误差对比

4 结论

本文中，笔者针对铅酸蓄电池的荷电状态进行预测分析，建立铅酸蓄电池的等效模型，分析改进型 LMBP 较一般型 LMBP 算法的区别与优势，提出一种基于改进型 LMBP 神经网络 SOC 预测的模型。对该模型进行仿真与验证得出结论是，用改进型 LMBP 神经网络模型对电池 SOC 的预测方法可行，且其估计结果与速度都高于标准 LMBP 模型的。因此，这种预测方法在实际工程运用中可有效地提高铅酸蓄电池的利用率与寿命。

参考文献：

[1]魏东涛, 黄之杰, 孔华, 等.蓄电池 SOC 的研究及预测方法[J].电源技术, 2016, 40(6): 1321–1323.

[2]史步海, 朱学峰.LMBP 神经网络改进算法的研究[J].控制工程, 2008, 15(2): 165–168.

[3]黄业伟.电动汽车锂离子动力电池健康状态估计方法研究[D].合肥: 合肥工业大学, 2014.

[4]赵轩, 康留旺, 汪贵平, 等.基于 BP 神经网络的SOC 估计及铅酸蓄电池特性[J].电源技术, 2014,38(5): 874–877.

[5]赵旭峰.LMBP 神经网络算法改进及其应用[D].北京: 中国科学技术大学, 2013.

[6]何明前, 范世军, 王显承, 等.基于 BP 神经网络的镉镍电池放电特性预测[J].电源技术, 2016,40(8): 1618–1664.

[7]张持健, 陈航.锂电池 SOC 预测方法综述[J].电源技术, 2016, 40(4): 1318–1333.

[8]商云龙, 张承慧, 崔纳新, 等.基于模糊神经网络优化扩展卡尔曼滤波的锂离子电池荷电状态估计[J].控制理论与应用, 2016, 33(2): 212–220.

[9]封进.BP 神经网络预估锂离子电池 SOC 训练数据选择[J].电源技术, 2016, 40(2): 283–286.

[10]王文生, 滕青芳, 刘特.电动车蓄电池 SOC 估计的神经网络方法[J].计算机与应用化学, 2015,32(6): 744–748.