数学分析中数学结构的层次关系

高婷婷，张明会

（陇南师范高等专科学校，甘肃成县742500）

数学分析中数学结构的层次关系

高婷婷，张明会

（陇南师范高等专科学校，甘肃成县742500）

在对结构思想概括介绍的基础上，进一步揭示了整个数学体内的结构层次关系。提出整个数学是建立在集合的基础上。首先是集合，一旦在集合的元素之间引进了一些关系，集合的元素就有了自己的个性和特征，然后再根据关系的性质，在集合上形成结构。

数学分析；数学结构；层次；分析

1 数学结构的层次框架

布尔巴基在集合上首先建立了三个基本结构：即代数结构、序结构和拓扑结构，并称它们为母结构。然后，在母结构的基础上，根据“亲缘”关系，交叉产生新的边缘结构；或者由二个以上母结构联合产生复合结构；或者在一个母结构上加上一些公理产生新的子结构。这样通过结构的反复交叉、复合、变换，形成了各种各样的数学分支，从而就形成一个有内部结构的整个数学世界。

布尔巴基以三个母结构为中心，按照结构交叉、复合、变换，将整个数学系统由一个分支发展到另一个分支，由一个层次延伸到另一个层次，一直延伸到未开垦的处女地。其结构层次框图如图1所示。

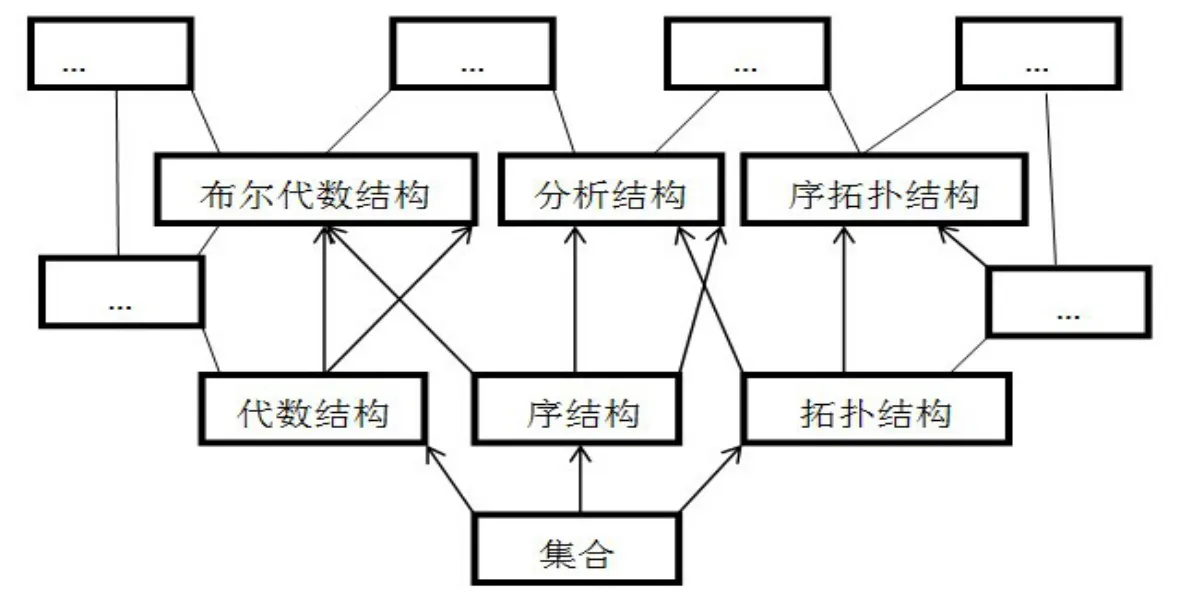
图1 布尔巴基数学结构层次图

2 母结构简介

由于母结构是整个数学结构的核心，又是实数R结构的基础，所以揭示实数R结构的特征之前，必须对三个基本结构有所了解。

2.1 代数结构

集合上建立了运算（来自数量关系），就能够从两个元素生出第三个元素，从而在此基础上就产生了代数结构。具体地讲，由离散对象、代数运算及其公理组所构成的结构系统统称为代数结构。例如，大家熟知的群、环、域、线性空间等。下面仅就域的结构为例作简要介绍。

L(T)：＜R；+，∙＞满足下列公理：

L1:R中的所有元素关于代数运算“+”满足结合律，即

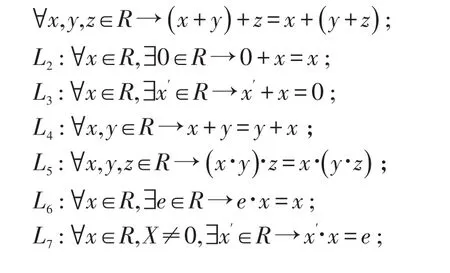
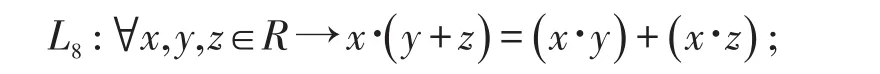
则称代数结构＜R；+，∙＞为域。

2.2 序结构

集合中某些元素有先后顺序关系（来自时间观念），从而在此基础上就产生了序结构。具体地讲，由集合中的序关系及其公理组所构成的数学结构称为序结构。例如，数的大小关系，生物的亲缘长幼关系，类的包含关系等。下面就全序和半序结构分别作简要介绍。

2.2.1 全序结构

L(T):＜A；R＞如满足下列公理：

L1：A中的元素关于关系R具有“自反性”，即

x∈A→xRx；

L2：A中的元素关于关系R具有“反对称性”，即

∀x,y∈A,若 xRy且 yRx，则 x=y；

L3：A中的元素关于关系R具有“传递性”，即

∀x,y,z∈A,若 xRy且 yRz，则 xRz；

L4:A中的任意两个元素关于关系R具有“可比性”，即

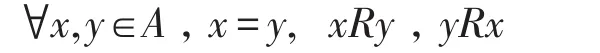
三种可比性关系中有且仅有一种成立。所以可比性亦称“三歧性”或“三分律”。则称数学结构＜A；R＞为全序结构。

例如，自然数集N,关于关系“≤”满足全系公理，所以数学结构＜N；≤＞是一个全序结构。

2.2.2 半序结构

L(T):满足全序结构前三条公理的数学结构＜A；R＞称为半序结构。

显然，半序集再加上可比性就是全序集。正因为半序集放宽了要求，所以适应范围就比全序集广。

2.3 拓扑结构

所谓拓扑结构，就是用来描述集合元素的连续性、分离性、临近、边界（这些概念来自空间经验）性质的数学结构。

由于拓扑结构是指能够描述极限和连续性的那种数学结构，而极限和连续性又是建立在领域概念的基础上的，因此，为了在一般意义上进行拓扑概念，一种比较直观而较简单的办法是引进邻域和邻领域结构。

L1：A中的每一个元素x在邻域集B中至少有一个包含它的邻域ux，即

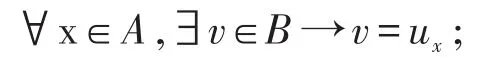
L2:A中的任一个元素在B中的任何两个邻域之交仍是该元素在B中的一个邻域，即

L3:若V是A的一个子集，而A中元素x的一个邻域ux又是v的子集，则v必是B中x的一个邻域，即

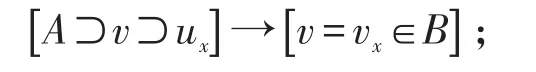
L4：A中任何一个元素x的任何一个邻域ux中必含有x的一个邻域vx,使得当A中的元素y∈vx时，总有 vy∈vx，即

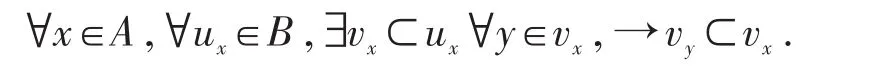
根据上述四条公理，就能保证在数学分析的论域内任一点x，能选取一连串越来越小的邻域使之以点x为极限。因此，邻域公理系统可以导致极限概念。正是由于邻域公理系统能描述极限和连续，而拓扑变换正好是研究在变换下连续性不变的那种变换。所以，人们亦称公理系统为拓扑结构。

On the Hierarchical Relationship of Mathematical Structure in Mathematical Analysis

GAO Tingting，ZHANG Minghui
(Longnan Normal College Department of mathematics,Gansu 742500，China)

This paper in the structure thought is summarized and introduced based on,further reveals the whole mathematics in vivo hierarchy.Put forward the mathematics is built on the basis set.First is set,once between the elements of the set introduced some relationship,elements of the set have their own personality and characteristics,and then according to the nature of the relationship,in the collection structure formation.

mathematical analysis;mathematical analysis;structural level;analysis

郝安林）

0151.2

A

1673-2928（2018）02-0093-02

D01:10.19329/j.cnki.1673-2928.2018.02.026

2017-01-03

高婷婷，女，甘肃礼县人，陇南师范高等专科学校讲师，研究方向：基础数学。