基于环介数的复杂作战网络节点重要度评估*

李清韦, 刘俊先, 陈　晨

(1.国防科技大学, 湖南 长沙　410073;2.解放军32145部队, 河南 新乡　453000)

近年来,国内外的学者对复杂网络节点的重要度评估提出了许多有价值的方法,例如节点删除法[1]、节点收缩法[2-3]、介数法[4-8]、效率矩阵法[9-11]、度中心性指标[12-15]等,用综合节点的局部重要度和全局重要度来评价节点在网络中的重要性。节点删除法和节点收缩法考虑最多的是无向复杂网络。介数法、效率矩阵法、度中心性指标这三种方法既可以用于无向网络,又可以用于有向网络。文献[16]定义虚拟的理想“核心节点”,将灰色关联度作为测度,评价网络中每个节点和理想“核心节点”的关联度,算法的时间复杂度为O(n2)。文献[17]引入环排序,是基于闭路径检测的排序量度,利用通过节点或者边的环所占权重进行重要度划分,适用于有向网络。以上每种测量方法既有优点,也存在一些不足,但都没有重点考量网络中存在的回路,不适用于解决本文研究的问题。

未来作战环境高度不确定性决定了体系需要更强的适应性,体系作战能力将随之而变化。而体系作战就是一个庞大而复杂的作战网络,其中作战节点的重要性程度相差较大。确定其中较为关键的作战节点,能增强体系作战能力的适应性,有针对性提升体系作战能力,发挥体系作战“1+1>2”的效果。在体系作战中各个节点之间的信息传递都是定向的,整个作战体系形成一个复杂的有向网络。根据OODA作战环理论,作战网络包含很多的环路,而现有网络测量方法对网络中存在的回路很少涉及,不太符合指挥控制作战的特点。基于以上考虑,结合作战的实际需求,本文提出了一种基于环介数的复杂作战网络节点重要度评估方法。

1　理论基础

1.1　问题提出

网络中的最关键节点往往不是网络的几何中心,所以网络节点的重要性评估问题不仅仅是发现网络图形的几何中心,更重要的是发现在人们所关心的几个状态上表现特别的节点。通过节点重要性评估找出那些重要的“核心节点”,一方面可以重点保护这些“核心节点”提高整个网络的可靠性,另一方面也可以攻击这些“薄弱环节”达到摧毁整个网络的目的。找出复杂作战网络中最重要的作战节点是至关重要的,能更有效地增强整个体系的作战能力。作战网络与其他网络虽有许多相似之处,但也存在诸多不同。利用判定普通网络中关键节点方法来判断作战网络的“关键节点”明显是行不通的。那么,要如何有效且合理地找出复杂作战网络中最重要的作战节点?本文围绕如何确定复杂作战网络中的作战节点的重要程度展开了研究。

1.2　作战环

作战网络是一个典型的复杂网络,它由许多作战节点以及节点间关联关系组成。作战节点主要包括观察、判断、决策和行动等,节点间的关联关系主要包括命令传达、数据交换和信息传递等。根据OODA环理论,指挥控制作战的特点就是按照观察—判断—决策—行动(OODA) 环路进行的战斗[18-19],作战网络中必然存在很多环。在作战过程中有大量的定向信息和数据交换,由此在复杂作战网络中就形成了一条条的相似于OODA环的环路。

作战网络中的环路与普通图中环路的不同之处在于作战网络中的环路是按照OODA环的规律构成的,作战环大致有两种形式：一是按照观察、判断、决策和行动的路径成环；二是反馈机制路径,将下一节点效果反馈回上一节点。因此,作战网络中的环路具有以下特征:一是复杂性,体系作战网络是节点间通过相互作用而产生复杂行为模式的整体;二是不确定性,作战环容易受到随机性、模糊性、粗糙性和不精确性等影响;三是整体性,每条环路是一个不可分割的整体,环路存在于更大的作战网络整体中。

2　复杂作战网络节点重要度分析

2.1　相关定义及计算方法

在计算作战节点重要度时主要考虑了经过作战节点环路的数目，并且参考了介数的定义，定义环介数来表示作战节点的重要度。

定义1图：一个具有n个作战节点的复杂作战网络可用G=(V,E)表示，其中V=(v1,v2,…vi,…vn)是网络的顶点集，E=(e1,e2,…ei,…em)是网络边的集合。图G相对应的邻接矩阵用01矩阵A表示，A中元素用eij表示，其中

定义2介数：介数通常分为节点介数和边介数两种，节点介数定义为网络中所有最短路径中经过该节点的路径的数目占最短路径总数的比例，边介数定义为网络中所有最短路径中经过该边的路径的数目占最短路径总数的比例。介数反映了相应的节点或者边在整个网络中的作用和影响力，是一个重要的全局几何量，具有很强的现实意义。

设网络具有n个节点，则节点i的介数指标定义为

式中，σst表示节点s和节点t之间的最短路径数，σst(i)表示节点s和节点t之间经过节点i的最短路径数。

同理，可计算边介数。

定义3作战环：指为了完成特定的作战任务或者作战目的，由观察、判断、决策、行动等作战节点构成的闭合回路。作战网络中的作战节点间关系构成环路简化了路径选择的控制，但作战网络中某条环路上各作战节点间是直接串联的，这样任何一个节点出了故障都有可能造成整条环路的中断。用阶数k来表示环路的大小，具有n条边的环路就称为n阶环。如果作战环路越长，阶数则越大，越容易遇到随机性、模糊性、粗糙性和不精确性等影响，作战环所面临的风险和不确定性也随之增加，在作战时被破坏或阻碍的概率也会较大。

定义4环路数：在复杂作战网络中经过某一作战节点的环路的总数即为环路数，符号为L。作战网络中环路的总数用Ltotal表示。将复杂作战网络用邻接矩阵表示，根据布尔运算规则，邻接矩阵乘幂表达的是矩阵的可达信息，可利用可达矩阵判断任意两节点之间是否有环路。当邻接矩阵的k次幂的主对角线上第i行的值不为0时，表示第i个节点存在k阶环，若为0，则表示不存在k阶环。矩阵的主对角线上各个元素之和被称为矩阵的秩，而矩阵的迹就等于A的特征值的总和。由此可推算作战节点的环路数。

记作战网络的邻接矩阵为A，dim(A)=n，则

1)作战节点i的环路数Li为

(1)

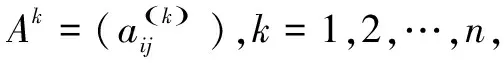
2)记A的特征根为λ1,λ2,…,λn(含重根)，可知

(2)

则在作战网络中所有的环路总数Ltotal为

(3)

定义5环介数：参照介数的定义，我们将作战节点的环介数定义为复杂作战网络中通过该作战节点的环路数占作战网络中环路总数的比例，符号为BL。

作战节点i的环介数BLi为

(4)

式中，Ltotal≠0，本文是在作战网络存在环路的情况下展开研究的，若Ltotal=0说明作战网络中无环路，则无展开研究的意义。环介数的值域为[0,1]，环介数值的大小代表作战节点的重要程度，环介数的值越大表示作战节点越重要。当作战节点的BL=0时，表示作战网络中所有的环路都不经过该节点；当作战节点的BL=1时，表示作战网络中所有的环路都经过该节点。

2.2　估值上限

对于单个作战节点，其环路数最大值为环路总数Ltotal，即作战网络中所有的环路都经过该节点，此时该作战节点的环介数BL=1；其环路数的最小值为0，即作战网络中所有的环路都不经过该节点，此时该作战节点的环介数BL=0。

3　算法

3.1　算法思想

作战网络不便于计算统计，故需将其转化为一个用0和1表示的邻接矩阵。0表示作战节点i到作战节点i+1没有信息和数据的传递；1表示作战节点i到作战节点i+1存在信息和数据的传递。若要找到复杂作战网络中所有的环路，必然要遍历整个作战网络。本文采用深度优先遍历算法对所有作战节点进行遍历。核心思想是从第一个作战节点开始遍历，找出与第一个作战节点存在信息和数据的传递的作战节点，然后从该作战节点开始遍历，找出与该作战节点存在信息和数据的传递的作战节点，再接着遍历，若能遍历回到最开始的作战节点，则所有遍历的作战节点形成了一个环路，然后输出。如不能回到最开始的作战节点则说明没有环路，然后从下一个作战节点开始遍历，此时不再遍历第一个作战节点所在行，若有环路则输出，若无环路接着往下遍历。依此规律进行遍历，直至遍历到最后一个作战活动，结束程序。

3.2　算法的时间复杂度

利用环介数评估作战网络节点的重要度是全局性的，要对所有的作战节点进行深度遍历。对单一作战节点进行深度遍历时，要将邻接矩阵中所有的点遍历一次，邻接矩阵中共有n2个点，故每个作战节点的计算复杂度为O(n2)。当遍历完n个作战节点时，总的计算复杂度为O(n3) 。

3.3　算法步骤

复杂作战网络中节点重要度评估的算法如下：

1)将作战网络图转换成邻接矩阵A输入，同时输入作战节点数n。

2)从邻接矩阵的的第一个点开始进行深度遍历，有环路则输出，无环路则往下遍历。直至遍历完所有节点。

3)计算每个作战节点经过的环路数L，计算作战网络总的环路数Ltotal。

4)计算每个作战节点的环介数BL。

5)将作战节点的环介数从小到大排序，从而确定网络中每个作战节点的重要程度。

4　算例分析

4.1　特殊作战网络

虽然大部分作战网络比较复杂，但有一些作战网络节点之间存在由构造所决定的有规律的连接关系。作战节点之间连接关系存在一定的规律，其环介数也具有类似的规律可循。本节主要介绍几种特殊的作战网络，探究作战节点数目n与其环介数BL的关系。

如图1所示，网络中共有n(n≥4)个节点，每个节点都与中心的指挥节点1有相互连接关系，再与左右两个邻居节点有相互连接关系。由于节点的连接关系相同，故每个节点(除中心指挥节点1外)的环路数相同。每个节点分别与左右两个邻居节点构成一个2阶环，所有除指挥节点外的节点构成一个逆时针的n阶环和一个顺时针的n阶环，k(2≤k≤n-2))个相邻节点都能与指挥节点1构成一个逆时针的k+1阶环和一个顺时针的k+1阶环，故节点i(除中心指挥节点1外)的环路数Li=n2-n+3，中心指挥节点1的环路数L1=2n2-5n+3，网络总的环路数Ltotal=2n2-4n+4，则节点i(除中心指挥节点1外)的环介数BLi=(n2-n+3)/(2n2-4n+4) ，节点1的环介数BL1=(2n2-5n+3)/(2n2-4n+4)。结果如图2所示，纵轴表示中心指挥网络的节点数目，横轴表示节点的环介数。由图2可知，当网络中节点数目足够多时，中心节点的环介数趋近于1，其余节点的环介数趋近于0.5。

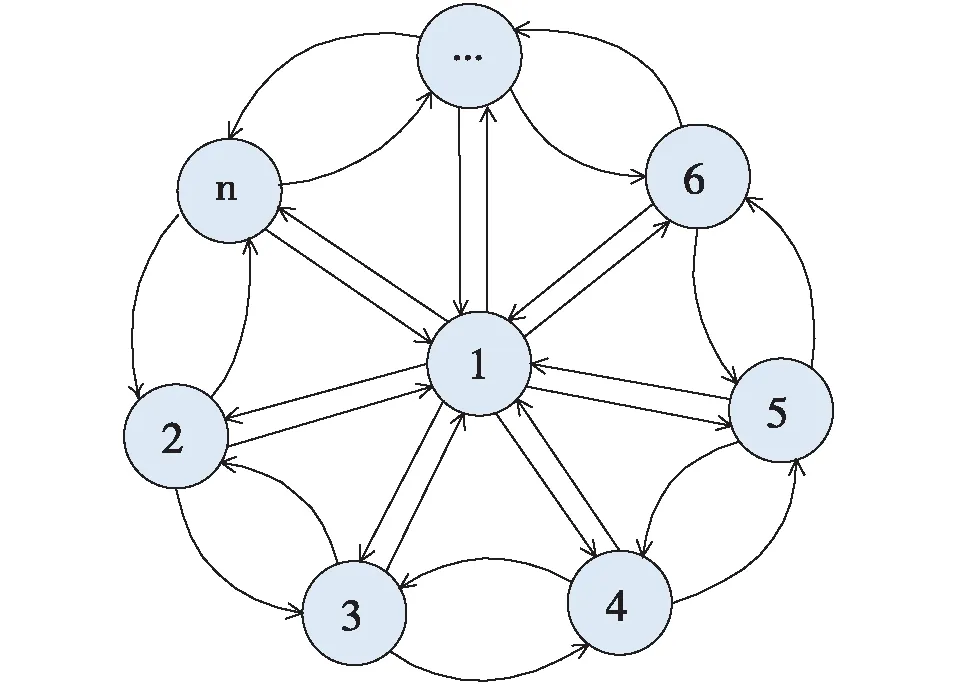
图1　中心指挥网

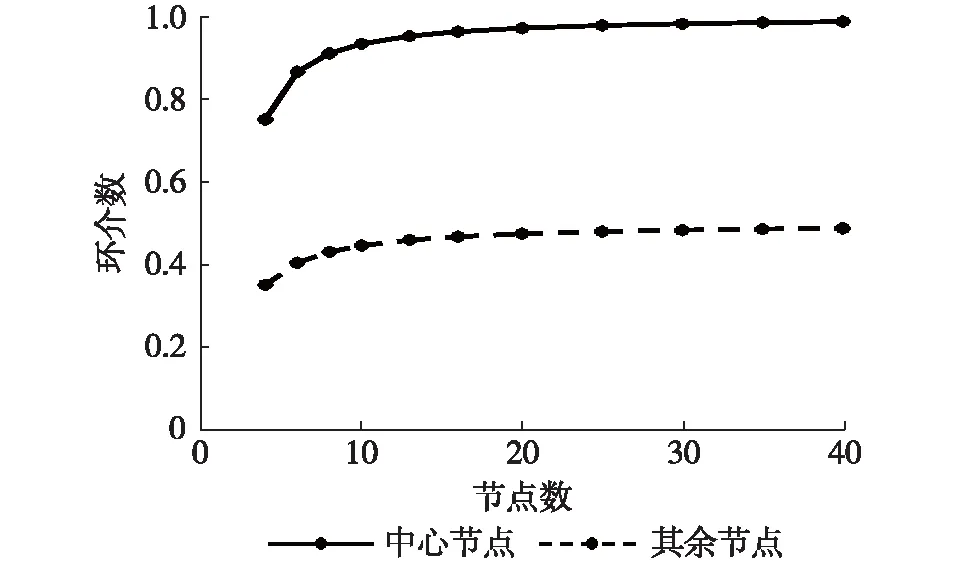
图2　中心指挥网络节点的环介数

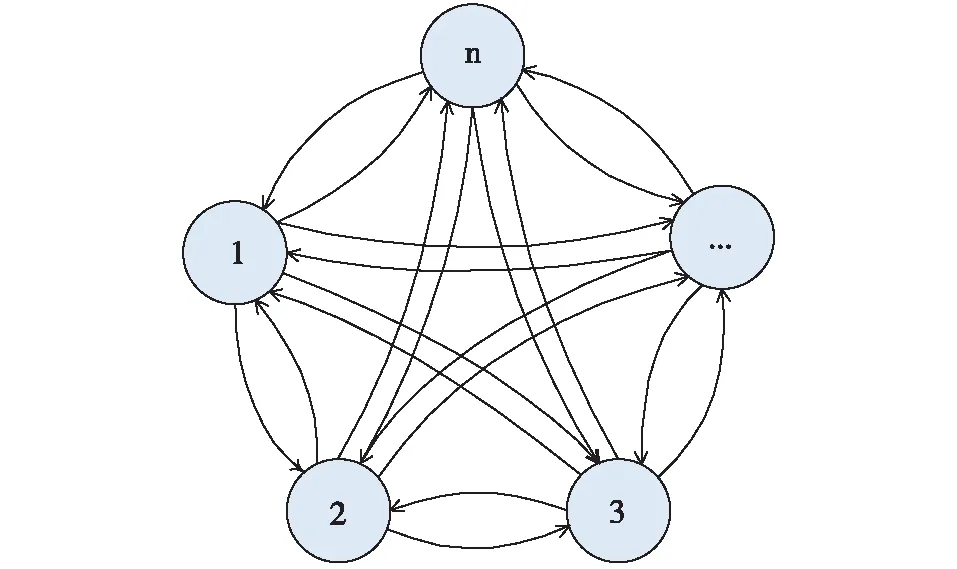
图3　全连接网络

4.2　实例分析

对于作战网络来说，利用环介数来确定作战节点的重要度是一个很好的衡量标准。在这里我们明确讨论环形的小世界网络的情况，如图4所示。如果我们仅考虑外圈的边，则所有信息可以在任何两个节点之间以顺时针或逆时针方向上两种方式交换，在这种情况下，所有信息都可以被节点认为同样重要。从节点0出来的快捷边(节点0→3,节点0→5,节点0→8)，节点0将比沿着网络的其他顶点起更为重要的作用。图中节点可分为3类，一类是快捷边的起点，如节点0；一类是快捷边的终点，如节点3、5、8；还有一类是普通节点，如节点1、2、4、6、7、9。

图4　小世界网络

图中共有18条环路，有10条环路经过节点0，8条环路经过节点3、5、8，7条环路经过节点1、2、4、6、7、9。各节点的环介数如表所示。本文还采用了介数(BC)、节点出入度(DEG)和文献 [17]三种方法计算该网络节点的重要度，结果如表1所示，表中的数据经过处理，使各个方法计算结果在0到1之间。从表中可见，各方法对重要度的评价存在着差异，评价指标选取的不同导致了这种差异。本文方法与介数法和文献[17]的结论存在微小差异，但文献[17]的计算过程更为复杂，利用介数计算节点重要度也较为复杂。本文方法与利用节点出入度计算方法得出的结论是一致的。各个方法得出的结论大致相似，最为重要的节点是节点0，其次是节点3、5、8，证明了本文方法的正确性与有效性。

表1　节点重要度评估结果

5　结束语

本文针对体系作战中的作战节点重要度进行了定量分析,采用作战节点环路数和环介数两项指标来确定复杂作战网络中最关键的作战活动,并与其他几种方法的结论进行对比。研究表明,利用环介数这一指标可以有效地分析作战节点的重要程度。确定作战网络中关键的作战节点,既可以针对敌方的关键作战节点进行精确打击,破坏敌方的作战网络;又可以对我方关键的作战节点进行针对性的加强,大幅提升体系作战能力。在下一步的研究中,可尝试通过作战节点环路的分析确定作战能力环路,通过作战节点重要度分析体系作战能力的重要性。

参考文献:

[1]Yang Wang, Zengru Di, Ying Fan. Identifying and Characterizing Nodes Important to Community Structure Using the Spectrum of the Graph[J]. PLoS ONE,2011, 6(11):e27418.

[2]谭跃进,吴俊,邓宏钟.复杂网络中节点重要度评估的节点收缩方法[J].系统工程理论与实践,2006, 26(11): 79-84.

[3]朱涛,张水平,郭戎潇,等.改进的加权复杂网络节点重要度评估的收缩方法[J].系统工程与电子技术,2009,31(8):1902-1905.

[4]王小光,王锋,李森.基于介数影响矩阵的通信网络节点重要度评价方法[J].空军工程大学学报(自然科学版),2012,13(5):80-84.

[5]Kazumi Saito, Masahiro Kimura, Kouzou Ohara, Hiroshi Motoda. Super mediator—A new centrality measure of node importance for information diffusion over social network [J]. Information Sciences, 2016(329):985-1000.

[6]Nicolas Kourtellis, Tharaka Alahakoon, Ramanuja Simha, Adriana Iamnitchi, Rahul Tripathi. Identifying high betweenness centrality nodes in large social networks [J]. Soc. Netw. Anal. Min.，2013(3):899-914.

[7]Taras Agryzkova, Jose L. Oliverb, Leandro Tortosac, Jose Vicentc. A new betweenness centrality measure based on an algorithm for ranking the nodes of a network [J]. Applied Mathematics and Computation, 2014, 244: 467-478.

[8]Marc Barthelemy. Betweenness Centrality in Large Complex Networks [J]. Physics of Condensed Matter. DOI: 10.1140/epjb/e2004-00111-4.

[9]范文礼,刘志刚.一种基于效率矩阵的网络节点重要度评价算法[J].计算物理,2013,30(5):714-719.

[10] 周 漩,张凤鸣，等.利用重要度评价矩阵确定复杂网络关键节点[J].物理学报, 2012,61(5):1-7.

[11] 范文礼,刘志刚. 基于传输效率矩阵的复杂网络节点重要度排序方法[J].西安交通大学学报,2014,49(2):337-342.

[12] 王欣,姚佩阳,周翔翔,等.指挥信息系统网络节点重要度评估方法[J].北京邮电大学学报,2011,34(5):38-42.

[13] 叶春森,汪传雷,刘宏伟.网络节点重要度评价方法研究[J].统计与决策, 2010,301(1):22-24.

[14] 任卓明,邵凤,刘建国,等.基于度与集聚系数的网络节点重要性度量方法研究[J].物理学报,2013,62(12):128901-1-5.

[15] 陈静,孙林夫.复杂网络中节点重要度评估[J].西南交通大学学报,2009,44(3):426-429.

[16] 张益.一种定量评估复杂网络节点重要度的算法[J].计算机工程,2011,37(20):87-89.

[17] Valery Van Kerrebroeck, Enzo Marinari. Ranking by Loops: a new approach to categorization[J]. Physics, 2008.

[18] 朱江,蔡蔚等. 基于OODA指挥控制环的作战仿真实验[J].指挥控制与仿真, 2015, 37(3):112-115.

[19] 黄建明, 高大鹏. 基于OODA环的作战对抗系统动力学模型[J].系统仿真学报, 2012, 24(3):561-564.