一种深度生成模型的超参数自适应优化法
姚诚伟, 陈根才
(浙江大学 计算机科学与技术学院,杭州 310027)
0 引 言
深度生成模型(Deep Generative Model, DGM)[1]作为深度学习模型的重要分支之一,不仅在各类监督学习领域取得优异的效果[2-4],而且在很多非监督学习领域领中有着独特的优势,如降维分析[5]、信息检索[6]、特征提取[7]等。DGM包括两种经典模型:深度置信网络(Deep Belief Network, DBN)[7]和深度玻耳兹曼机(Deep Boltzmann Machine, DBM)[8]。该类深度模型的共同特点是它们都由一种称为受限玻耳兹曼机(Restricted Boltzmann Machine, RBM)[7]的基本构件层层堆叠而构成的,因此DGM也是一种多层图概率模型。利用这种基于图概率模型的逐层训练策略,DGM可以非常好地对大量数据进行非监督方式的多层次特征提取[1],大大提升其在大数据分析和人工智能中应用效果。
尽管DGM在各类机器学习任务中取得极大成功,然而如其他深度模型一样,在面对实际数据和应用时,DGM的部署和训练是一件非常困难的事。主要原因是DGM有着众多的超参数,在利用实际数据对模型进行训练之前必须为这些超参数设置合适的值,否则在训练中深度模型的参数很容易崩溃或无法学到有用的特征[9]。这些超参数包括:学习速度、动量系数、参数惩罚系数、丢弃比例、batch的大小,以及定义网络结构的超参数等等。由于深度模型的训练需要巨大的计算资源,人工多次尝试选择合适的超参数不仅需要丰富的经验,而且非常费时费力。
为此,近年来面向机器学习的超参数自动优化方法越来越得到学术界的重视。目前,比较主流的方法是基于黑盒的贝叶斯优化方法,其中具有代表性的有基于时序模型的算法配置(Sequential Model-based Algorithm Configuration, SMAC)[10]、Parzen树估测(Tree Parzen Estimator, TPE)[11]和Spearmint算法[12]。由于这些方法需要重复多次运行被优化模型,以获取优化所必需的验证误差,所以在优化深度模型时它们的效率很低。另一种思路是自适应的优化方法,目前比较主流的方法有AdaGrad[14]、AdaDelta[15]、 RMSProp[16]、Adam[17]等。但这些方法大多只对学习速度进行优化,无法同时综合优化多个超参数。
本文利用DGM逐层训练的特点,提出一种以神经元激活的稀疏度(sparsity of Hidden Units, SHU)为目标值,利用高斯过程(Gaussian Process, GP)[18]动态对多个超参数进行同时优化的方法。神经元激活状态往往被领域专家用于监控DGM的训练过程是否处于理想状态。在训练的中间阶段,每一隐藏层的神经元被激活太多或太少都会降低特征的提取效果。因此,本文利用当前迭代时神经元激活状态,通过比较不同超参数组合下,神经元激活状态的变化,利用GP预测其中最合适组合,进行下一迭代的训练。该方法的优势在于通过自适应的策略同时优化多个超参数,毋需象传统贝叶斯方法那样重复训练整个模型,同时自适应的策略也大大提升DGM的特征提取的性能指标,以及对不同网络结构的稳定性。
1 深度生成模型

图1受限玻耳兹曼机(RBM)示意图
深度生成模型是一种垂直多层的图概率模型,它的基本构件是RBM[7],如图1所示,其中双线圆圈代表输入神经元,细线圆圈代表隐藏层神经元。RBM最大的特点是各层内部神经元之间没有链接,这大大加快了层与层之间的随机采样效率。输入层可以接受各种类型的数据,包括:二进制、实数和k组(k-array)数据。以二进制为例,假设v∈{0,1}D为输入层,h∈{0,1}F为隐藏层,则RBM的能量公式定义如下[1]:
E(v,h;θ)=
(1)
式中:W为单元之间的连接参数;a,b为偏离项。为简化表达,设θ={W,a,b},则模型的联合概率定义如下[1]:
(2)

(3)
(4)
式中,g(x)=1/(1+e-x)。RBM训练的目的是获得优化的参数W,为此,Hinton和他的小组提出了对比散度(Contrastive Divergence)的算法[1]:
ΔW=α(EPdata[vhT]-EPT[vhT])
(5)
式中:α为学习速度,EPdata[·]为数据依赖期望值,EPT是利用Gibbs链近似所得的模型依赖期望值。
利用RBM堆叠,根据结构和训练策略的差异,DGM又分为两大经典模型:DBN和DBM,如图2所示。其中,DBN是混合概率图模型,除了顶层为无向图以外,其他各层均为有向图;DBM则是完全无向图,它们的训练方法详见文献[1]。

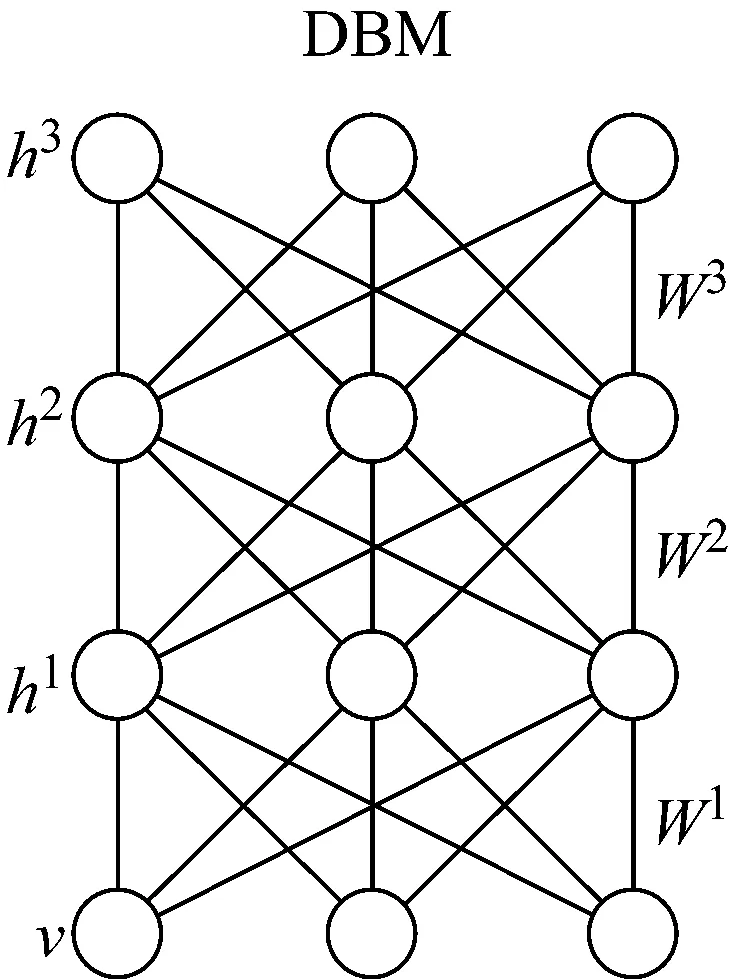
图2深度置信网络(DBN)与深度玻耳兹曼机(DBM)
图中hi代表第i层隐藏层神经元所组成的向量;Wi代表各层间的连接参数。
就像其他很多深度模型一样,训练DGM最大的挑战就是防止模型的过度拟合和参数崩溃。为此很多辅助机制被提了出来[9],如:利用动量原理防止参数的巨烈波动;利用参数惩罚机制防止参数崩溃;利用丢弃部分神经元或它们的链接方式防止过度拟合;以及根据训练集合理设计网络结构等等。这些辅助机制大大提升DGM的性能,然而为了调整和控制这些辅助机制,众多的超参数也被发明出来,其中最为常用如表1所示。针对新的训练任务时,即使领域专家也很难一蹴而就找到的这么多超参数的优化组合配置。

表1 深度生成模型的常用超参数的说明
2 超参数优化算法
在训练DGM时,大量的实践经验表明:在少数情况下被激活的神经元比大多数情况下被激活的神经元更加有价值[9]。因为对于一个有效的DGM来讲,当特点神经元被激活时,表示模型从特定数据中探测到了特定的特征。图3显示了训练RBM时的4个模拟例子,其中3个是不理想的状态,一个为理想状态。在此模拟例子中,数据的类别顺序是被打乱的。其中,图3(a)显示隐藏层中大部分的神经元被激活,很可能模型的参数W变得过大导致无法识别有效特征;图3(b)则是图3(a)反面,大部分神经元都无法被激活,很可能参数变得过小而失去探测特征的能力;图3(c)是一个有趣的例子,表示不管给任何数据,其中部分神经元总是被激活,导致神经元的利用率不高;图3(d)是相对比较理想的状态,当某一数据到来时只会激活其中部分神经元。
为在训练过程中得到较好的神经元激活状态,提出了一种神经元稀疏度的惩罚项,利用交叉熵的方法实现实际激活比例与目标激活比例之间的调和[9]。与此同时,一个新的超参数——稀疏度惩罚系数被发明了出来。该方法无法把多个超参数之间相互微妙的影响关系考虑进去。因此,本文提出一种新的以神经元激活的稀疏度为目标值,利用GP对稀疏度进行预测,并选出可能使神经元激活状态较优的超参数组合的方法。


图34个模拟RBM训练中隐藏层神经元激活状态图,其中横坐标表示隐藏层的神经元序号,纵坐标表示min-batch的大小
该方法的优化法策略是在每次迭代时,先固定当前的超参数,通过前一节描述的训练过程学习模型的参数W;然后固定W,利用GP学习并预测超参数。

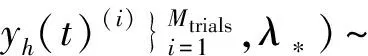
(6)
μy*=m(λ*)+K*K-1(y-mλ(i))
(7)
(8)
式中:y*为预测的稀疏度;K是利用GP的协方差函数[18]从λ(i)计算的协方差矩阵,K*=k(λ*,λ(i)),K**=k(λ*,λ*);mλ(i)为由GP的均值函数[18]对λ(i)计算所得。利用式(6)得出的后验分布,可以快速从众多超参数候选中选出最佳超参数的组合。
算法1基于高斯过程超参数优化算法(在epoch:t)
输入A(Vtrain),被优化的模型;
Vtrain为训练集;
λbest上次迭代的最佳超参数配置;
Mtrials用来建立GP模型的样本数量;
Mpredict预测最佳超参数的尝试样本数量;
interval采样样本的定义域范围;
输出λbest预测的最佳超参数配置;
1.fori=1 toMtrialsdo
2.在λbest±interval范围内随机产生一个随机配置λ(i);
3.λ(i)用训练模型A(Vtrain),计算yh(t)(i);
4.end for
5.forj=1 toMpredictdo
6.在λbest±interval范围内随机产生一个随机配置λ(j);
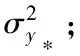
8.利用公式(9)选择新的λbest;
9.end for
10.returnλbest。

(9)
式中,λbest为上一epoch的最佳组合。
3 实验分析
在实验分析中,为验证本方法在以下3个方面的性能表现:
(1) 优化效率对比。与目前主流的超参数优化方法(SMAC和TPE)进行对比,验证本方法对DGM的超参数优化效率。
(2) 针对不同DGM网络结构时性能的稳定性分析。
(3) 在实际文本聚类的学习任务中,验证本超参数优化方法在非监督学习中的优越表现。
3.1 超参数优化效率的分析
这里对比包括本方法(SHU)在内的不同的超参数优化方法,比较它们对DGM的优化速度。在DGM中选取其中两种最经典的模型:DBN[7]和DBM[8](见图2)。
对比的超参数优化方法包括两种目前最主流的优化器*http://www.automl.org/HPOLIB:SMAC[10]和TPE[11],具体采用了它们针对深度模型的改进型*https://github.com/automl/pylearningcurve predictor。测试数据选择MNIST手写体数字,其中包括60 000个训练样本和10 000个测试样本,每个样本为28×28像素的手写体1~9的阿拉伯数字。
在针对MNIST分类任务中训练DBN和DBM一般划分两个阶段:预训练和精调。本方法主要针对预训练阶段。预训练阶段,SHU和SMAC、TPE针对模型的初始化设置详见表2、3。此外目标稀疏度选择为0.05。本方法在用到GP时,length-scale参数和noise参数分别设为1和0.1。在精调过程中同样集成SMAC和TPE作为优化器,并给予相同的设置。整个训练过程的epochs设为100。测试指标为分类精度。
图4、5分别给出了在DBN和DBM上优化速度的对比,结果显示SHU比SMAC和TPE收敛速度更快,同时训练过程中的大部分时间内SHU可以取得对比方法约一半的错误。因此,该自适应的方法不仅可以明显提升优化速度,并且帮助DBN和DBM提升分类精度。

表2 本方法针对模型的超参数初始化设置

表3 SMAC和TPE针对模型的超参数初始化设置
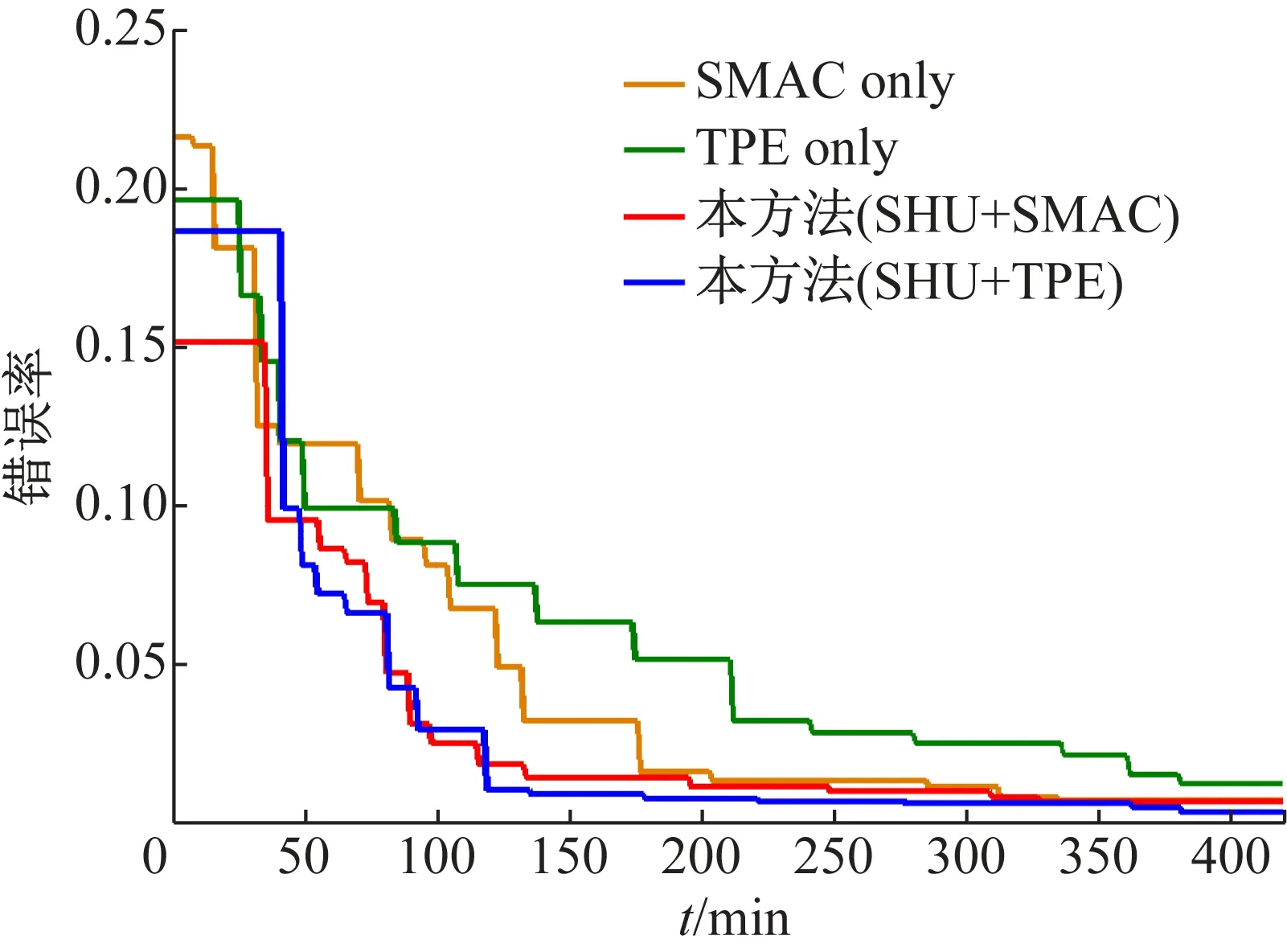
图4 DBN在MNIST上分类实验中学习曲线的对比
3.2 针对不同网络结构的稳定性分析
初次使用DGM的人员由于经验不足,往往会为选择什么样的网络结构而困扰。本文提出的自适应超参数优化方法,最大的优势之一在于可以很大程度减轻由于网络结构设置的差异而带来的性能的巨大变动。本小节的实验重点验证不同网络结构下,自适应超参数优化方法的稳定性。为了显示本方法的优势,我们与手工超参数设置进行比较。
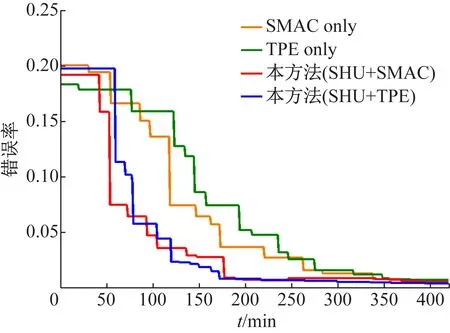
图5 DBM在MNIST上分类实验中学习曲线的对比
这里选择深度模型为DBN,测试数据集仍是MNIST,验证标准也是错误率。根据多次尝试,手工选择一个较为优化的超参数组合:[η,α,ε]=[0.5,1.0,0.000 1],其中η为动量系数,α为学习速度,ε为参数惩罚系数。针对自适应方法,目标稀疏度同样选择0.05,[η,α,ε]的初始化与表2相同。实验中选择4种不同的网络结构,分别为[784, 100]、[784, 200, 200]、[784, 500, 100]、[784, 400, 200, 100],如图6所示。GP的length-scale参数和noise参数分别设为1和0.1。

图6 不同DBN网络结构下的性能比较
图6展示的实验结果显示,不同DBN的网络结构下自适应超参数优化方法取得的错误率明显低于手工设置超参数方法的错误率,并且性能相对较为稳定。从比较结果可得,本方法可以帮助提升DBN在实际应用中的稳定性。
3.3 针对文本聚类的实验分析
DGM最大的优势在于能够利用非监督学习较好地提取数据的特征。本小节选取文本聚类这一典型的非监督学习任务,利用自适应的超参数优化对DBN进行优化,并将结果与目前主流的文本聚类算法,以及手工选取超参数的DBN做对比,验证本方法的优越性。
这里选用的数据集是Reuters-21578数据集,它是由路透社提供并被Lewis*http://www.daviddlewis.com/resources/test collections/reuters21578/优化过的数据集。选取30个类别,其中包括8 293篇文章和18 933个词汇。当去掉词缀、词根以及停用词后,选取其中出现频率最高的3 000个词作为字典。
对比的方法包括:PLSA[19]、LDA[20]、NCut[21]、NMF[22]、lapGMM、Auto-encoder、DBN(手工调整超参数)[7]。由于本方法是面相超参数优化的,为公平起见,为对比方法也选择了目前主流的超参数优化器:SMAC。但是SMAC优化器需要根据训练效果的某个目标值,才能进行优化,这里采用了Perplexity[20]:
(10)
式中:M是文档集D的大小;P(wi)是文档中各个词的概率,可以在各自算法的推理过程中得到;li是第i篇文档的长度。为SMAC选取最大迭代预算为50。
采用DBN的网络结构是[4 000, 900, 400, 400, 30],相应超参数初始化:[η,α,ε]=[0.5,1.0,0.000 1],目标稀疏度仍设为0.05,GP的length-scale参数和noise参数分别设为1和0.1。实验的评价指标为最终聚类的精度。
表4给出了Reuters-21578上文本聚类的实验结果。结果显示基于神经元激活稀疏度(SHU)的自适应超参数优化方法,不仅明显提升DBN在文本聚类的性能效果,而且在聚类精度上优于目前主流的文本聚类算法。图7进一步展示针对整个文本集,DBN最后一层神经元激活的状态,显示当文本属于某个类别时,总是有特定的神经元会被激活,表明了基于自适应优化方法的DBN在特征提取的有效性。
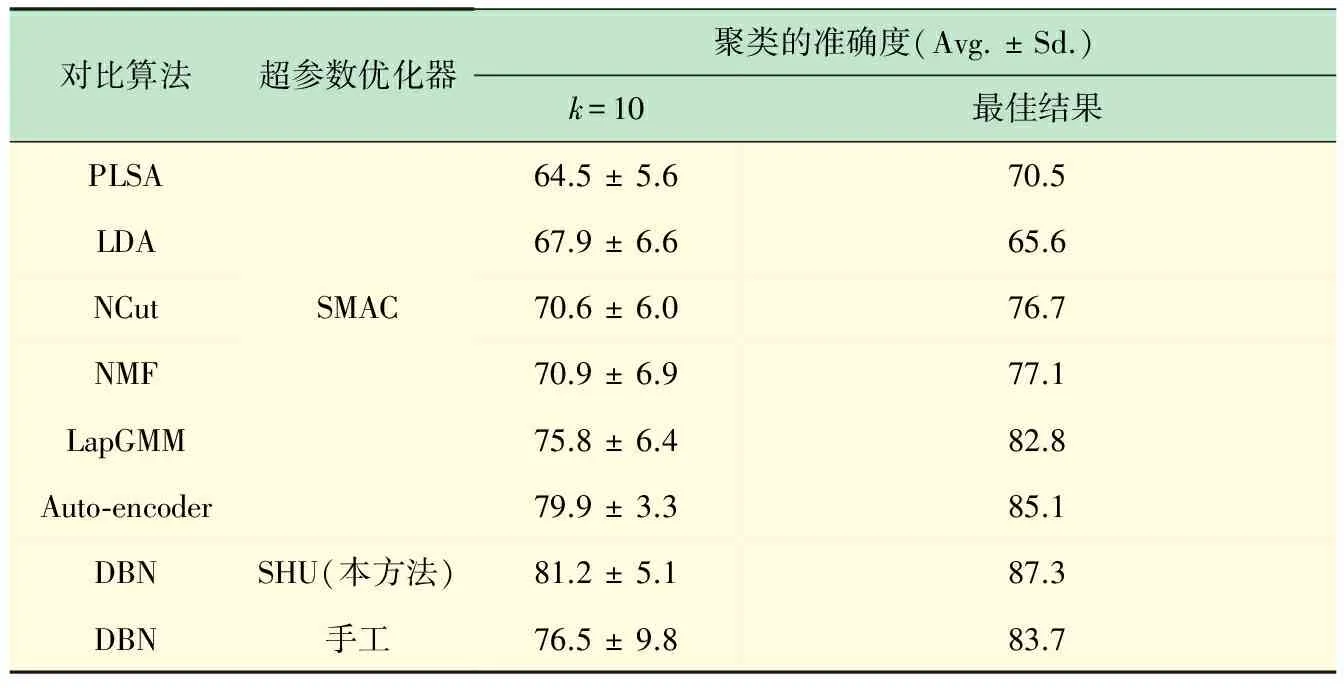
表4 Reuters-21578上文本聚类的实验结果

图7 Reuters-21578上DBN最后一层神经元激活状态
4 结 语
本文提出了一种针对DGM的超参数自适应优化方法。该方法可以在每一epoch的训练过程中,根据各隐藏层神经元激活度的变化,利用GP对最合适的超参数组合进行预测,并将预测所得超参数用于下一epoch的训练。该方法能够在实验研究和实际应用中,明显提升DGM优化效率。并且,由于该方法对不同网络结构的稳定性较好,因此可以帮助缺乏DGM实验和应用经验的人员快速上手。进一步实验也显示在文本聚类的学习任务中,该方法能够获得比主流方法更好的性能。
参考文献(References):
[1]Salakhutdinov R. Learning deep generative models[J].The Annual Review of Statistics and Its Application at Statistics. Annualreviews.org, 2015, 2(1):361-385.
[2]Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553):436-444.
[3]Bengio Y, Lamblin P, Popovici D,etal. Greedy layer-wise training of deep networks[C]// International Conference on Neural Information Processing Systems. MIT Press, 2006:153-160.
[4]Larochelle H, Bengio Y, Louradour J,etal. Exploring strategies for training deep neural networks[J]. Journal of Machine Learning Research, 2009, 1(10):1-40.
[5]Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786):504.
[6]Salakhutdinov R, Hinton G. Semantic hashing[J]. International Journal of Approximate Reasoning, 2009, 50(7).
[7]Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7):1527.
[8]Salakhutdinov R, Hinton G. An efficient learning procedure for deep Boltzmann machines[J]. Neural Computation, 2012, 24(8):1967.
[9]Hinton G E. A Practical Guide to Training Restricted Boltzmann Machines[M]// Neural Networks: Tricks of the Trade. Springer Berlin Heidelberg, 2012:599-619.
[10]Hutter F, Hoos H H, Leyton-Brown K. Sequential Model-Based Optimization for General Algorithm Configuration[M]// Learning and Intelligent Optimization. Springer Berlin Heidelberg, 2011:507-523.
[11]Bergstra J, Bardenet R, Kégl B,etal. Algorithms for Hyper-Parameter Optimization[C]// Advances in Neural Information Processing Systems, 2011:2546-2554.
[12]Snoek J, Larochelle H, Adams R P. Practical bayesian optimization of machine learning algorithms[J]. Advances in Neural Information Processing Systems, 2012, 4:2951.
[13]Domhan T, Springenberg J T, Hutter F. Speeding up automatic hyperparameter optimization of deep neural networks by extrapolation of learning curves[C]//AAAI Press, 2015.
[14]Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization[J]. Journal of Machine Learning Research, 2011, 12(7):2121-2159.
[15]Dauphin Y N, Vries H D, Bengio Y. Equilibrated adaptive learning rates for non-convex optimization[J]. Computer Science, 2015, 35(3):1504-1512.
[16]Rasmussen C E, Williams C K I. Gaussian process for machine learning[M]// Gaussian processes for machine learning. MIT Press, 2006:69-106.
[17]Hofmann T. Unsupervised learning by probabilistic latent semantic analysis[J]. Machine Learning, 2001, 42(1):177-196.
[18]Blei D M, Ng A Y, Jordan M I. Latent dirichlet allocation[J]. Journal of Machine Learning Research, 2003, 3:993-1022.
[19]Ng A Y, Jordan M I, Weiss Y. On spectral clustering: Analysis and an algorithm[J]. Proceedings of Advances in Neural Information Processing Systems, 2002, 14:849-856.
[20]Bao L, Tang S, Li J,etal. Document clustering based on spectral clustering and non-negative matrix factorization[C]// International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems, 2008.
[21]He X, Cai D, Shao Y,etal. Laplacian regularized gaussian mixture model for data clustering[J]. Knowledge & Data Engineering IEEE Transactions on, 2011, 23(9):1406-1418.
[22]Vincent P, Larochelle H, Bengio Y,etal. Extracting and composing robust features with denoisingautoencoders[C]// ICML, 2008:1096-1103.
·名人名言·
想像力比知识更重要,因为知识是有限的,而想像力概括着世界上的一切,推动着进步,并且是知识进化的源泉。严肃地说,想像力是科学研究中的实在因素。
——爱因斯坦

