基于“M+N”理论的近红外光谱血糖无创测量方法
徐馨荷, 王晓飞
(北京信息科技大学 仪器科学与光电工程学院,北京 100192)
0 引 言
血糖是人体一项极为重要的生理指标,血糖浓度的相对恒定对维持机体,尤其是脑、神经的正常生理功能有着非常重要的意义[1-2]。目前血糖浓度测量方法主要有自动生化仪测量法和快速血糖仪测量法[3],都是通过采血的方式来检测血糖值,给患者带来创伤,对患者长时间的血糖监测不利,故无创血糖检测的实现具有十分重要的现实意义。然而,由于信号微弱、测量条件变化复杂、人体生理背景难以定量等问题对光谱测量的影响进而导致血糖预测精度不高,达不到临床使用需求,是目前近红外无创光谱血糖测量突出的难题[4-5]。因此探究新的测量方法以克服测量条件、人体生理背景等对光谱测量的影响来提高测量精度,对全面实现血糖的无创测量具有重要意义。
“M+N”理论[6-7]从误差理论的角度分析测量系统和测量过程,将被测对象自身的差异和其他干扰因素一同归于整个测量系统中,系统地考虑两者对测量精度的影响。本文研究无创血糖测量中的影响因素,并根据“M+N”理论将影响因素分成“M”因素和“N”因素,依据影响因素的特性采用不同的方法减小其对血糖预测值的影响。
1 “M+N”理论
“M+N”理论中“M”表示被测对象中的M种非测量组分;“N”表示影响被测成分测量精度的N种外界干扰因素[6]。其提高测量精度的关键在于将“M”因素与“N”因素同等对待,判断其为系统误差还是随机误差,同时提出必要的解决办法。图1所示为“M+N”理论框图。
图1中影响因素E1、E2、E3、E4如表1所示。其中:E1为影响血糖测量的血液组分及其他非测量组分[8];E3是现今无创血糖测量研究的热门之一;E2和E4分别是“M”因素和“N”因素中随机误差的典型代表。
根据各因素的不同属性对其有不同的处理方法来降低其对血糖测量值的影响,本文采用单沿提取法减小接触压力带来的影响,并将甘油三酯、高密度脂蛋白胆固醇、血清总胆固醇、年龄纳入模型中,系统地考虑这4种因素对血糖测量值的影响[8-9]。
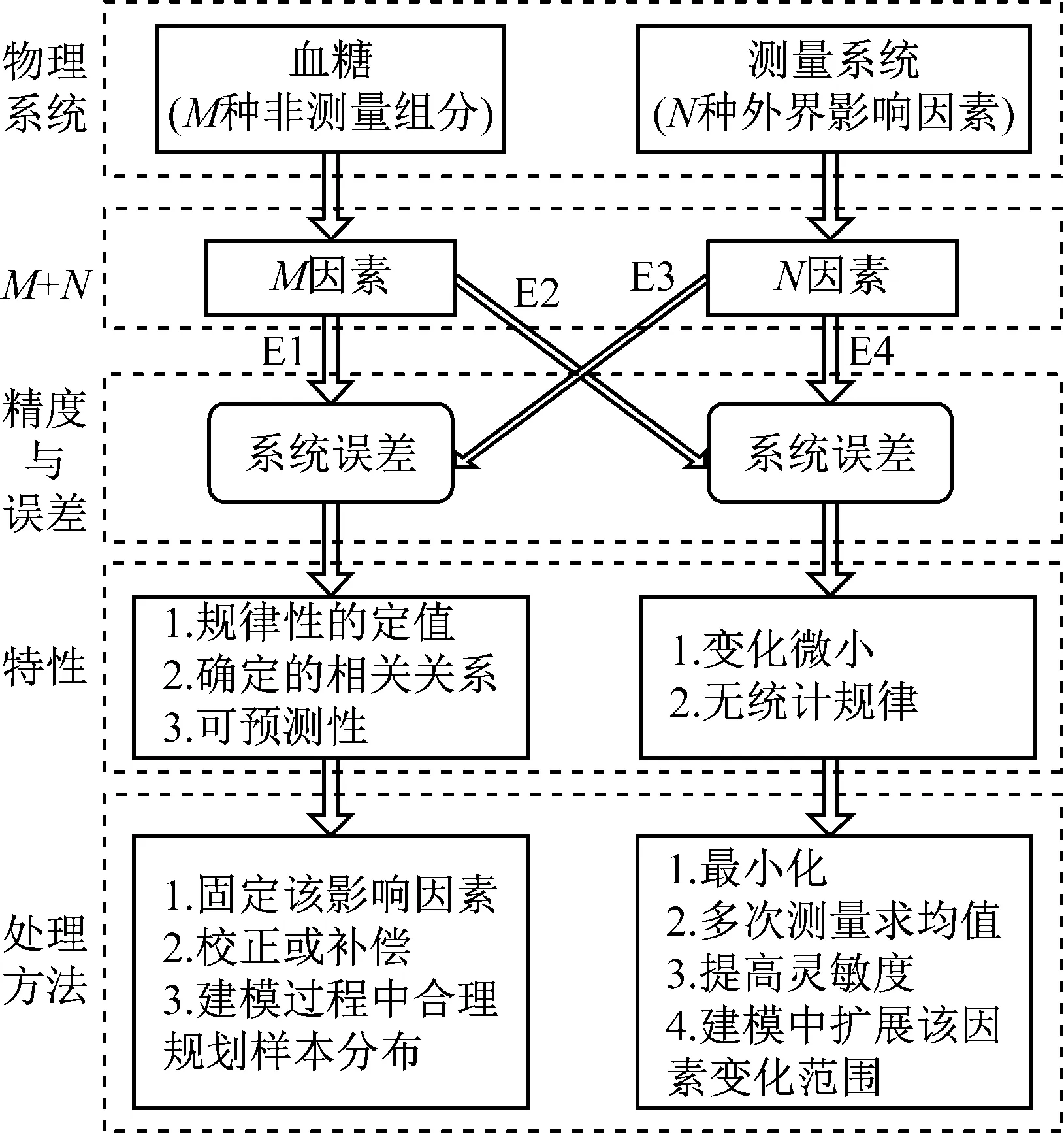
图1“M+N”理论结构框图

表1 “M”因素和“N”因素的分类
2 实验装置
图2所示为基于“M+N”理论的人体试验系统,其中光源为50 W的溴钨灯,实验所用光谱仪为AvaSpec-HS1024x58TEC高灵敏度型光纤光谱仪,波长范围为200~1 160 nm。本次实验被测对象为239名患者,受测者平卧放松将食指指端完全遮挡住光纤入口,光源发出的光聚焦透过手指后,由光谱仪直接进行光谱数据的采集,并由计算机保存采集到的光谱数据。
光谱数据采集完成后,对受试者进行静脉抽血,获得血糖真值以及胆固醇、甘油三酯等血液其他组分数据并记录患者的年龄。由于在脉搏波的采集过程中,光强及其他检测条件的影响,本次实验选取的波长范围是580.43~900.81 nm。波长间隔为0.94 nm,约560个波长。
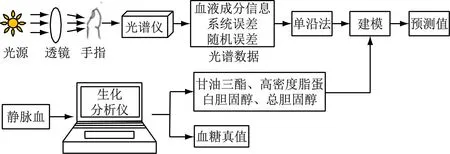
图221基于“M+N”理论的人体试验系统
3 数据分析及结果讨论
3.1 光谱样本选择
为了提高基于动态光谱的多波长血糖建模方法的稳定性和可靠性,需要评判动态光谱质量。本文采用的方法是利用动态光谱数据稳定波长数的多少来进行光谱数据质量的评判[10]。稳定波长数是各波长下对数脉搏波频域基波分量频率持续一致的波长个数。图3所示为单个样本的脉搏波频率图,可看出,对数脉搏波在1.2 Hz处连续出现,共560个波长,在该处所覆盖的波长个数即为稳定波长数。稳定波长数越大则表明各波长下对数脉搏波越相似,即动态光谱数据质量越高。根据稳定波长数这一标准在原有的239组光谱样本中选取了192组光谱样本。
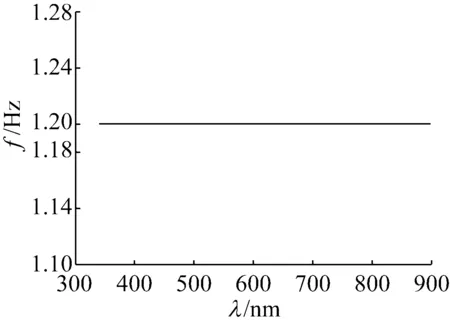
图3单个样本的脉搏波频率
3.2 单沿法
单沿提取法的基本思想是用统计平均的方法提取各波长下峰峰值的对应比例关系,并非直接提取峰峰值。该方法利用了对数脉搏波的叠加平均效应来剔除和校正各波长下脉搏波的波形误差,同时也利用了单沿动态光谱的叠加平均效应剔除含有粗大误差的单沿动态光谱,从两方面降低误差对波形的影响[11-13]。因此在数据预处理阶段选取单沿法提取动态光谱,可以减小“N”因素的系统误差——接触压力带来的影响。
单沿提取法的提取步骤如下:
(1) 对采集到的光电容积脉搏波信号取对数,并将其中强度较大的信号进行叠加平均,作为脉搏波的模板。
(2) 找到每个周期内的波峰与波谷值,通过峰谷值来确定上升沿和下降沿,将所有波长的有效上升沿与模板的有效上升沿进行最小二乘拟合,以此来校正对数脉搏波的上升沿。
任意波长λ下对数脉搏波在时域上如下式所示:
yλ(t)=ΔAλ·x(t)+DCλ
(1)
式中:ΔAλ为脉动动脉血液的吸光度值;x(t)为对数脉搏波的波形函数;DCλ为对数脉搏波的直流分量;对数脉搏波随时间t变化的出射光强为yλ(t)。
由于各波长下对数脉搏波的波形具有相似性,即x(t)是不变的,故对数脉搏波模板的出射光强值y0(t)可表示为:
y0(t)=ΔA0·x(t)+DC0
(2)
式中:ΔA0为对数脉搏波模板的平均吸光度;DC0为对数脉搏波模板的平均直流分量。
将式(1)、(2)合并,可以得到:
(3)
从式(3)可以看出,对数脉搏波模板的出射光强y0(t)为自变量,各波长对数脉搏波的出射光强yλ(t)为因变量,两者呈线性关系;斜率α=ΔAλ/ΔA0为经过最小二乘拟合得到的各波长的拟合斜率,将所有波长下的拟合斜率作为动态光谱的等效值,构成一系列单沿动态光谱。
(3) 采用欧式距离来判定单沿动态光谱与叠加平均值的相似性。计算每一个波长下单沿动态光谱与叠加平均值的欧式距离di(x,y)(i为单沿动态光谱样本数量),其几何表达式如下:
(4)
若d(x,y)越小,则表明单沿动态光谱与叠加平均值之间的相似程度越高。
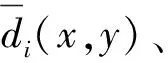
(4) 按照莱以特准则(3σ准则)判别单沿动态光谱是否含有粗大误差,
|δi|>3σ
(8)
若某单沿动态光谱满足3σ准则,则可判定该单沿动态光谱含有粗大误差,应予以剔除;否则认为该样本中不含粗大误差。对剔除粗大误差后的单沿动态光谱再进行上述操作步骤,直到全部剔除含有粗大误差的单沿动态光谱,筛选得到最终的有效动态光谱,之后进行叠加平均作为最终的单沿动态光谱输出。图4为单个样本经单沿提取法提取后的动态光谱图,其中该样本有效沿的个数为59个。
3.3 偏最小二乘法建立模型

图4 单沿法提取的动态光谱
偏最小二乘法[14-17](Partial Least Squares Regression,PLS)是一种数学优化技术,它提供一种线性回归建模的方法。PLS的原理如下: 将自变量矩阵X和因变量矩阵Y分别做标准化处理,得到:
E0=(E01,E02,…,E0p)n×p,F0=(F01,F02,…,F0q)n×q
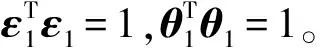
由拉格朗日算法可得出ε1和θ1:
(10)
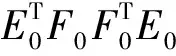
(11)
(12)
式中:E1和F1分别为以上2个回归方程的残差矩阵;回归系数向量p1和q1表示为:
(13)
此时若回归方程能够达到所需精度,可终止算法。否则,将利用X被t1解释后的残差和Y被u1解释后的残差来进行第2成分t2和u2的提取。即用残差矩阵E1和F1取代E0和F0求得ε2和θ2,并得到第2成分t2和u2,建立回归方程,有:
(14)
(15)
同样地,E2和F2为残差矩阵,回归系数向量是:
(16)
以此类推,设秩为A,可得到:
由于t1,t2,…,tA均可以表示为E0中各向量的线性组合,式(17)与(18)结合可表示为
(19)
式中:
本文采用PLS建立模型并进行血糖预测,将“M”因素系统误差中的甘油三酯、胆固醇、高密度脂蛋白胆固醇和年龄4个影响因素作为自变量矩阵
X=[x1,x2,x3,x4]
经单沿法提取后的光谱数据作为因变量矩阵Y=[y1,y2,…,yq],将这两部分数据作为模型的输入,模型输出为血糖预测值,如图5所示。
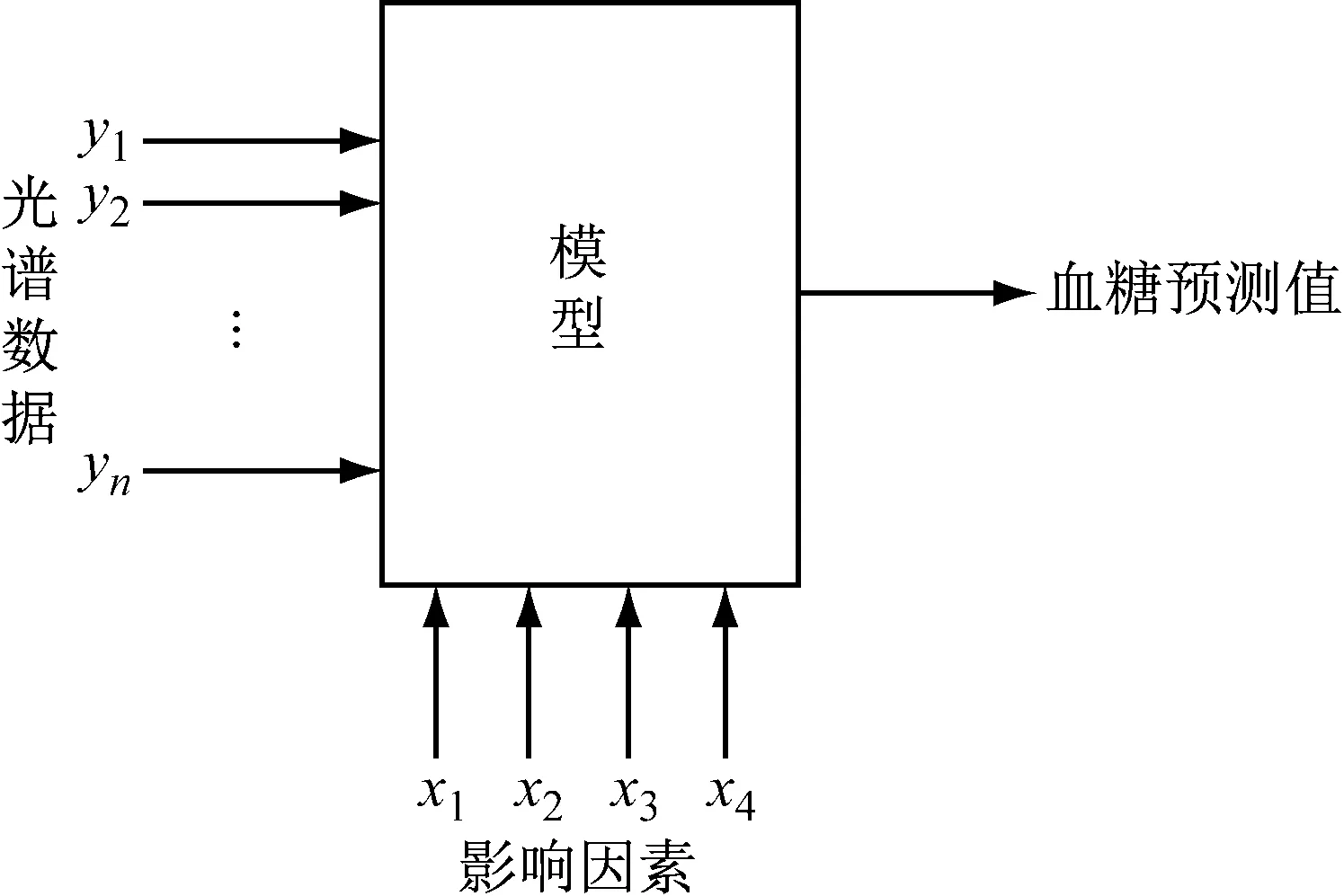
图5建立模型
采用相关系数和平均预测相对误差两个指标来评价模型,计算公式如下:
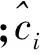
在192例样本中随机选取144例样本进行建模,48例样本进行预测。基于“M+N”理论的血糖模型预测值、未考虑其他非测量组分影响的预测值和血糖真实值的数据对比如表2所示。图6为基于“M+N”理论的血糖模型预测值与血糖真实值之间的相对误差。
基于“M+N”理论测量方法的血糖预测值和血糖真值的相关系数为0.929 5,平均预测相对误差为0.033,而未考虑其他非测量组分影响下的光谱数据与血糖真值的相关系数为0.828 5,平均预测相对误差为0.046。结果表明,基于“M+N”理论考虑非测量组分对血糖的影响这一测量方法的测量精度优于传统的测量方法。

表2 预测值与真实值的对比
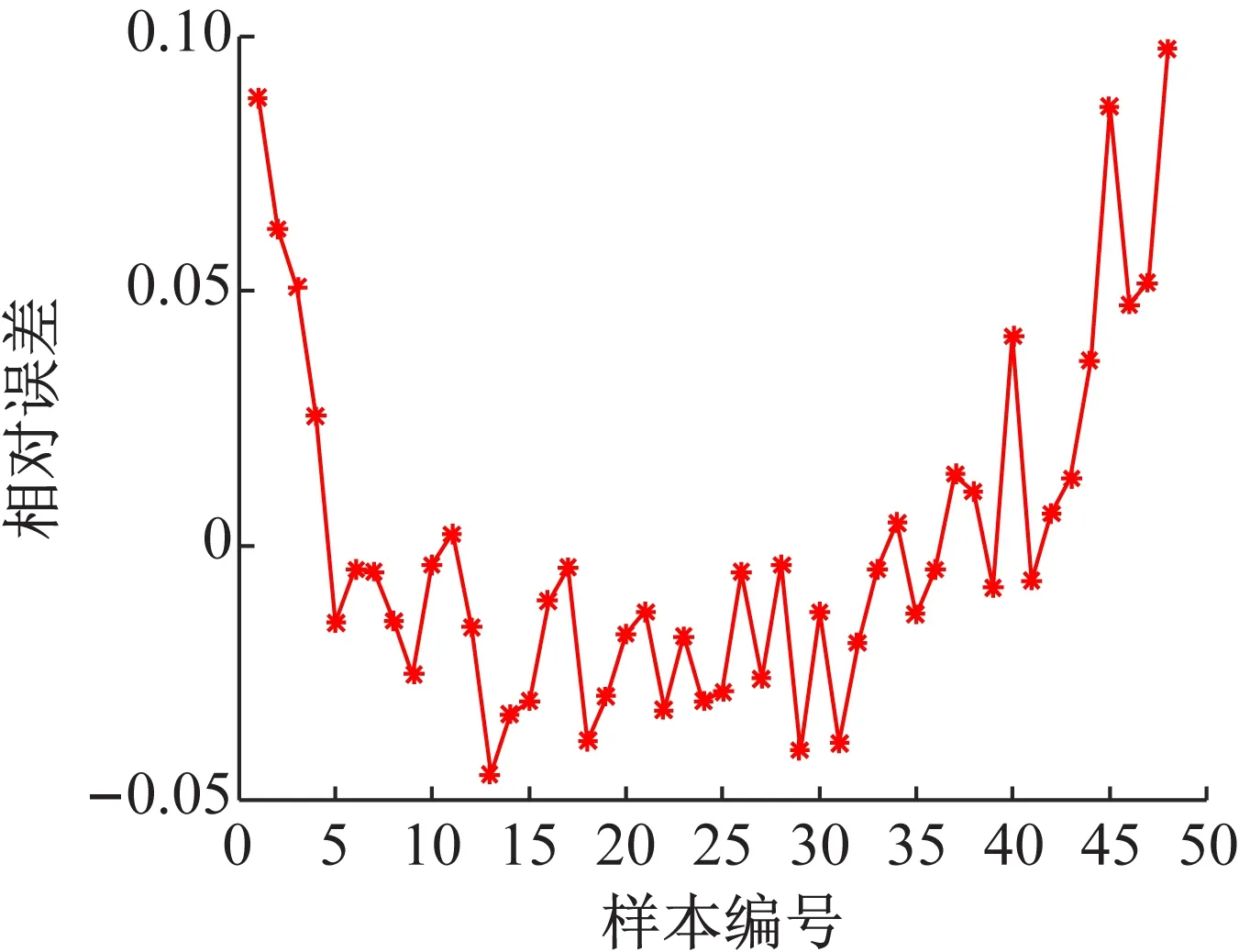
图6 基于“ M+N”理论的血糖预测值与真值的相对误差
4 结 语
“M+N”理论将被测对象和其他影响因素一同归于整个测量系统中,全面考虑了两者对血糖测量精度的影响。本文通过将“M”因素系统误差中的胆固醇、甘油三酯、年龄和高密度脂蛋白胆固醇四种非测量组分纳入模型,利用单沿提取法减小“N”因素系统误差中接触压力对血糖测量值带来的影响,使得血糖测量精度得以提高。这一方法可推广应用到其他血液组分的无创测量中。
参考文献(References):
[1]王连明, 辛晓敏, 刘晓民,等. 血糖测定的影响因素研究[J]. 中国实验诊断学, 2006, 10(11):1345-1347.
[2]Tamura K, Ishizawa H, Fujita K,etal. Application to noninvasive measurement of blood components based on infrared spectroscopy[J]. Ieej Transactions on Electronics Information & Systems, 2007, 127(5):686-691.
[3]石博雅. 牙齿与皮肤组织光学相干层析成像建模及应用研究[D]. 天津:天津大学, 2014.
[4]刘蓉, 徐可欣. 近红外光谱无创血糖检测中体温变化的影响分析[J]. 天津大学学报(自然科学与工程技术版), 2008, 41(1):1-6.
[5]Maruo K, Oota T, Tsurugi M,etal. New methodology to obtain a calibration model for noninvasive near-infrared blood glucose monitoring[J]. Applied Spectroscopy, 2006, 60(4):441-449.
[6]李刚, 李哲, 王晓飞,等. 测量模式的演进与“M+N”理论的提出[J]. 北京信息科技大学学报(自然科学版), 2013(2):9-13.
[7]李刚, 李哲, 李晓霞,等. 基于“M+N”理论的光谱分析中光源电压对预测精度影响的研究[J]. 光谱学与光谱分析, 2013, 33(6):1456-1461.
[8]李曼. 老年2型糖尿病患者腰围、体重指数与血糖、血压、血脂、尿酸的相关性研究[J]. 中西医结合心脑血管病杂志, 2015, 13(11):1351-1352.
[9]李丽, 王晓飞, 卢恺. 基于“M+N”理论的近红外光谱血氧饱和度无创测量方法[J]. 生物医学工程学杂志, 2016(5):885-889.
[10]李刚,王慧泉,赵喆,等. 动态光谱数据质量的评价[J]. 光谱学与光谱分析,2010,30(10);2802-2806.
[11]李刚, 熊婵,王慧泉,等.动态光谱的单拍提取[J].光谱学与光谱分析,2011,31(7):1857-1861.
[12]李刚, 周梅, 王慧泉,等. 动态光谱提取方法的对比研究[J]. 光谱学与光谱分析, 2012, 32(5):1324-1328.
[13]李刚, 王慧泉, 赵喆,等. 提高DS法无创血液成分检测信噪比的方法与分析[J]. 光谱学与光谱分析, 2012, 32(8):2290-2294.
[14]张宝菊,贾萍,张志勇,等. PLS在基于动态光谱的人体血液中性粒细胞无创测量中的应用[J]. 光谱学与光谱分析,2010(2):466-469.
[15]李朋成,朱军桃,马云栋,等. 基于偏最小二乘法的近红外光谱分析应用[J]. 测绘地理信息,2015(2):53-56.
[16]Delwiche S, Reeves J I. The effect of spectral pre-treatments on the partial least squares modelling of agricultural products[J]. Journal of Near Infrared Spectroscopy, 2004, 12(1):177.
[17]Fang J, Qiang J, Wei X. Simultaneous determination of main composition and additive in vinegar by NIR and partial least squares[J]. Computers & Applied Chemistry, 2010, 27(3):351-354.

