一种基于误差约束的动态聚焦最优分段方法*

罗汉武,孙 广,崔士刚,林 楠,王思奇,王 平*

(1.国网内蒙古东部电力有限公司检修分公司,呼和浩特 010020;2.重庆大学 输配电装备及系统安全与新技术国家重点实验室,重庆 400044)

在超声成像系统中,聚焦的本质是对不同通道接收到的回波信号施加特定的延时后相加求和,得到目标点的聚焦信号[1-3]。为了提高超声图像的横向分辨率,在波束合成过程中通常采用逐点聚焦。但是逐点聚焦需要大量的聚焦延时参数,在工程实现中存在较大难度[4-5]。考虑到逐点聚焦是一种聚焦点间距为极限小的动态聚焦,如果能在接收回波信号阶段采用分段聚焦,将大大减少聚焦延时参数的存储量,但这将会带来聚焦延时误差的问题[6]。通常接收阶段分段数越多,聚焦延时误差越小,超声回波信号的聚焦效果也越好[7-8]。简单地将探测深度均匀分段[9-10],会造成在近场区域聚焦延时误差较大;在中远场区域聚焦延时误差虽相对较小,但有分段冗余的现象[11]。

本文在聚焦延时误差给定的条件下,围绕如何在全程探测深度内实现最优分段、提高波束合成的聚焦精度,以及工程实现方法等方面进行了研究。

1 动态聚焦

假设线阵换能器子阵阵元数为N,相邻两阵元的中心间距为d,第i号阵元与阵元中心的距离为xi(如图1所示),则

(1)

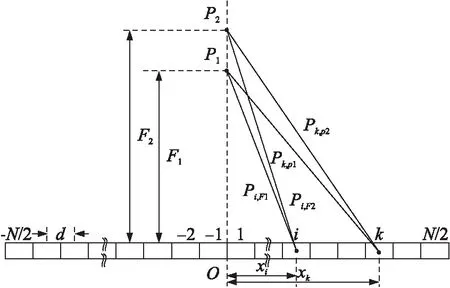
图1 线性换能器的聚焦延迟时间计算

从阵元中心O到焦点p1的距离为F1,第i号阵元与阵元中心线的距离为xi,则焦点p1到第i号阵元与阵元中心距离的声程差为[12]

(2)

于是,第i号阵元到焦点p1的延迟时间τi,p1为

(3)

式中:c为超声波的声速。

假设逐点聚焦成像深度为L,采样频率为fs,形成一条波束合成扫描线上焦点的个数N1和焦点间隔ΔF为[13]

(4)

在一个典型的128阵元32通道的相控阵超声诊断仪中,取L=240 mm,fs=50 MHz,如果采用逐点聚焦,每个聚焦延时参数采用2 bytes存储,那么聚焦延时参数的直接存储量M=2fsNL/c为495 kbyte。随着聚焦通道数的增加,在逐点聚焦过程中,各个聚焦通道的延时参数需要实时输出,这在工程实现上有一定的困难。由于受存储器数量和存储容量的限制,采用普通小容量的FPGA难以实现。

2 动态聚焦最优分段与延时参数生成

2.1 动态聚焦最优分段与误差优化

以线阵换能器为例,如图1所示。由于动态聚焦子阵相对于聚焦线是轴对称的,仅需考虑1～N/2阵元的聚焦延时时间。根据式(2)、式(3),第i、k号阵元分别在点p1和点p2聚焦时,时间延迟差为

(5)

如果k>i∈[1,N/2],且满足xk>xi,可以证明式(6)成立

|Δτk|-|Δτi|>0 (k>i)

(6)

因此,在同一段聚焦区域[F1,F2]内,如果|ΔτN/2|<δ,则有式(7)成立

|Δτ1|<|Δτ2|<…<|Δxi|<…<|ΔxN/2|<δ

(7)

根据式(7)可知,在聚焦区域[F1,F2],如果聚焦通道最边沿阵元的聚焦误差ΔxN/2控制在δ范围内,那么其他阵元的聚焦延时误差也必将小于δ。

所以,当聚焦延迟时间误差为δ一定时,可以按式(8)进行约束。

(8)

式中:τN/2,F0、τN/2,F1、τN/2,F2分别表示第N/2通道在探测深度F0、F1、F2处的延时参数。显然,在探测区域(F0,F2)范围内,如果按τN/2,F1进行聚焦,则聚焦延时误差必定小于δ。

当探测深度[F0,Fs]确定时,可按式(8)进行聚焦区域的依次分段,即可得到一系列的聚焦分段位置F0,F2,…,Fs和相应分段区间的聚焦延时参数τN/2,F1,τN/2,F3,…,τN/2,Fs-1。将定位误差进行分段处理,提高了不同探测深度误差的区分度,使得分段聚焦更加精确[14]。此时,可以根据式(9)计算出最优分段数Snum。

Snum=(τN/2,H0-τN/2,H

(9)

显然,在约束误差δ给定的情况下,当分段数小于Snum,式(8)将不成立。

根据式(8)确定分段聚焦的几何位置F0,F2,…,Fs,根据式(4)计算得到ΔF,考虑到AD转换器的数据个数N是整数,按式(10)计算得到聚焦的分段位置序数N0,N2,…,Ns。

N=[F/ΔF]

(10)

式中:F为几何分段位置,ΔF为逐点聚焦的间隔,[.]是取整运算。

以128阵元32通道的相控阵超声检测仪为例,取发射信号频率f0为3.5 MHz,AD采样频率fs为50 MHz,阵元中心间隔d为0.44 mm,声速c为 1 540 m/s,探测深度为2 mm～240 mm,约束误差δ为20 ns,根据式(8)和式(9),计算分段数为82段,如图2所示,分段聚焦延时参数如图3所示。

图2 分段数与探测深度的关系曲线

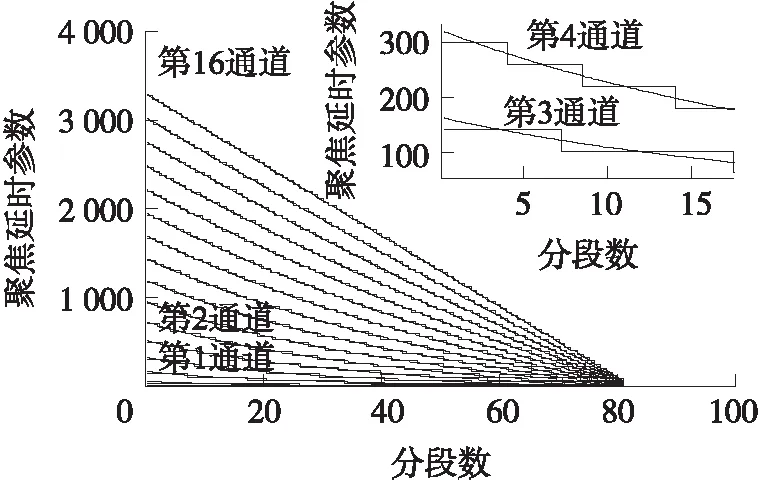
图3 基于误差约束的分段聚焦延时参数

由图2可见,动态聚焦延时参数在近场区域变化较快,分段较密集;而在中远场,聚焦延时参数变化相对缓慢,分段数较为稀疏。

从图3可以看出:分段聚焦延时参数为阶梯折线,且始终围绕精确的聚焦延时曲线上下波动,最大误差被控制在约束误差δ内。

考虑到聚焦通道越靠近聚焦中心线,聚焦延时参数的绝对数值越小。第k通道聚焦延时的相对误差可按式(11)进行计算。

Δεk=(Tk,j-τk,j)/τk,j=δ/τk,j

(11)

式中:Tk,j、τk,j分别为第k通道,深度为j时的分段聚焦延时参数和逐点聚焦延时参数,Δεk为第k通道聚焦延时参数的相对误差。

当聚焦延时约束误差δ一定,k越小,聚焦延时的相对误差越大。因此,在保持分段数不变的情况下,为了进一步提高聚焦精度,通过动态改变折线逼近单位λk来进一步提高折线向聚焦曲线逼近的精度。用Tk1,0、Tk2,0,分别表示k1与k2通道的聚焦延时初始值,根据式(3)计算可知:当F1≈0,k1>2k2时,Tk1,0>2Tk2,0。所以λk可以按式(12)进行动态调整。

(12)

采用λk代替式(8)中的δ进行约束,可以得到各个通道聚焦延时参数如图4所示。

图4 聚焦延时参数的高精度逼近

从图4可以看出,采用动态逼近单位λk约束后,靠近中心阵元通道聚焦延时的折线逼近精度提高了,这有助于进一步提高动态聚焦的波束合成精度。

如何确保学校近6万名师生的正常伙食供应，确保食品卫生安全呢？武汉理工大学后勤集团总经理、武汉理工大学食品药品安全工作站站长赵高山总结的六大机制很是到位。

2.2 延迟参数的压缩存储与实时生成方法

基于上述分段方法,图5给出了128阵元32通道J=82分段时,分段聚焦的阶梯折线与精确聚焦延时曲线满足|Tk,j-τk,j|<λk关系示意图。其中,横坐标为分段数,纵坐标为聚焦延时参数,逼近单位是λk。

图5 阶梯折线逼近聚焦延时曲线

由图5可以看出:当折线Tk,j数值修正时,相应分段用“1”表示,而其余分段用“0”表示。因此,对于一条阶梯折线Tk,j仅需要其初始值,逼近单位λk和分段数J个二进制位,即可完成对逼近折线Tk,j的描述。对于16通道折线的修正信息,可以将每一分段的16个通道的二进制位修正信息当作2 byte数据进行存储。

以图4为例,存储量分析如下:存储每个聚焦延时参数Tk,0(k=1,2,3,…,16)的初始值需要2 byte,则存储量M1为:M1=(N/2)×2=32 bytes。每个通道的逼近单位λk采用1 byte存储,则存储量M2为:M2=(N/2)×1=16 byte。聚焦延时参数T`k,j的实时修正需要根据分段位置和每一分段的修正信息才能实现。每一分段位置信息按2 byte存储,则存储量M3为:M3=J×2=164 byte。每一分段每一通道的修正信息为1位,则16通道修正信息的存储量M4为:M4=J×N/2/8=164 byte。因此,总的存储单元为M1+M2+M3+M4,即376 byte就可实现对图4中分段聚焦延时参数Tk,j(k=1,2,3…,16)的压缩存储。表1给出了约束误差δ为20 ns时,不同聚焦通道数时,直接存储与按本文方法存储的所需存储容量的对比。

从表1可以看出,随着通道数的增加,压缩效率有所降低,但64阵元时仍然达1/804。这表明本文所提出的分段方法能够大幅度减少聚焦延时参数的存储容量,从而有效解决逐点聚焦在工程中需大量存储空间而难以实现的难题。

表1 不同聚焦方法的存储容量对比

结合分段逼近的方法,分段动态聚焦延时参数实时生成的硬件框图如图6所示。

图6 聚焦延时参数发生器的硬件框图

工作原理:微处理器装载16通道的82个分段折线的修正信息到双口RAM,装载82个分段的位置序号到地址发生器[15],然后装载16个通道的聚焦延时初始数值Tk,0(k=1,2,3…,16)和逼近单位λk(k=1,2,3…,16)到相应的递减器中。当动态聚焦开始时,微控制器的IO启动地址发生器在FOCUS_CLK时钟作用下工作,当FOCUS_CLK时钟计数值与分段位置序号依次相同时,地址发生器依次输出分段序数ADDR[6..0],依次从双口RAM中取出16通道对应的每一分段的聚焦延时参数Tk,j的修正信息。各个聚焦通道的递减器在DEC_CLK信号作用下对该通道的聚焦参数Tk,j进行修正,如果BIT位为“0”,则不修正,如果BIT位为“1”,则相应通道的聚焦延时参数Tk,j递减1个逼近单位λk,从而实现图4中各个通道聚焦延时参数Tk,j的实时产生。

3 仿真分析与讨论

3.1 波形误差分析

设定超声波发射频率f0=3.5 MHz,采样频率为fs=50 MHz,允许约束误差δ=20 ns,此时,分段聚焦的采样点与逐点聚焦采样点最大相位差为φ=0.439 8 rad。取信号s0=sin(2πf0t+φ0),φ0为初相位。32通道回波信号精确聚焦延时叠加后信号为:

s1=32s0=32sin(ωt+φ0)

(13)

(14)

图7 分段聚焦与逐点聚焦合成信号的对比

通过MATLAB仿真得到s1和s2的波形如图7所示。

从图7可以看出,逐点聚焦与本文方法对某目标点进行探测时,若约束误差δ=20 ns,那么波束合成信号基本重合。MATLAB计算表明:s1和s2的相关系数为0.999 9,根均方百分比差异PRD(Percentage Root mean squared Difference)为0.027 6%。

3.2 点目标成像验证

利用Field Ⅱ[16]进行点散射目标仿真实验。所有仿真均采用定点发射的工作模式,采用线性阵列,仿真探头采用128个阵元32通道,发射信号频率为f0=3.5 MHz,系统采样频率fs=50 MHz,阵元中心间隔d=0.44 mm,声速我们选取人体软组织中的平均值c为1 540 m/s,发射焦点在50 mm处。信号仿真时加入60 dB的高斯白噪声,成像的动态范围为60 dB[17]。目标散射点共6个,其分别在(0 0 30)、(0 0 40)、(0 0 50)、(0 0 60)、(0 0 70)、(0 0 80)mm处,探测宽度为10 mm。图8中(a)为传统逐点聚焦方法成像效果,(b)为最优动态分段聚焦成像效果。

图8 点目标成像对比

图8(a)、图8(b)的结构相似性指标(SSIM:Structural Similarity index)[18]为0.947 7。对比图8(a)、图8(b)的成像效果可以看出:所提出的方法的成像效果与逐点聚焦成像效果基本一致。

假设时间窗内的逐点聚焦数据为x(t),分段聚焦波形为y(t)。表2给出了用MATLAB计算得到的6个目标点回波信号的相关指标。

表2 点目标及相应指标

从表2可以看出,6个目标点的相关系数ρxy大于0.97,根均方百分比差异PRD小于3%,SSIM指标大于0.970。这表明在相同声速的情况下采用本文方法的波束合成信号与逐点聚焦的波束合成信号高度相干,它们的幅值、相位等信息基本一致。

4 结束语

本文提出了一种基于误差约束的动态聚焦最优分段与误差优化方法,其核心思想是根据聚焦约束误差δ对探测深度进行最优分段,然后通过改变各个通道的逼近单位λk,从整体上进一步提高分段动态聚焦延时参数Tk,j的精度。在此基础上,提出了与之相应的聚焦延时参数压缩存储方法与实时生成算法,大幅度提高了聚焦延时参数压缩率,简化了聚焦延时参数的实时生成方法,避免了复杂的乘法、开方运算。实验数据分析与测试结果表明:所提出的方法在利用少量存储空间的情况下即可以实现与逐点聚焦基本一致的成像效果,从而为高精度超声聚焦成像的工程实现提供了一个有价值的参考。该方法对于凸阵探头仍然适用,也可以进一步拓展到非对称的聚焦领域,因此本文提出的算法具有较大的工程实用价值。

[1] Carlos F,Monsterrat P,Alberto I. The Progressive Focusing Correction Technique for Ultrasound Beamforming[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency,2006,53(10):1820-1831.

[2] 张慧,何常德,苗静,等. 一种基于MATLAB的CMUT阵列设计与成像仿真方法[J]. 传感技术学报,2014,27(4):490-494.

[3] 冯若. 超声手册[M]. 南京:南京大学出版社,1999:774-778.

[4] Noe Jimenez,Francisco Camarena,Nuria Gonzalez-Salido. Dynamic Nonlinear Focal Shift in Amplitude Modulated Moderately Focused Acoustic Beams[J]. Ultrasonics,2017,75:106-114.

[5] Vasudevan V,Govindan P,Saniie J. Dynamically Reconfig Urable Analog Front-End for Ultrasonic Imaging Applications[J]. IEEE International Ultrasonics Symposium,2014:1924-1927.

[6] Xiang Li,Zhiyuan Yao,Shengli Zhou,et al. Dynamic Modeling and Characteristics Analysis of a Modal-Independent Linear Ultrasonic Motor[J]. Ultrasonics,2016:117-127.

[7] Lertsilp D,Umchid S,Techavipoo U,el al. Improvements in Ultrasound Elastography Using Dynamic Focusing[J]. Biomedical Engineering International Conference(BMEiCON),2011:225-228.

[8] 李鹏,陈裕泉,胡大可,等. 超声成像系统中自适应动态滤波器的设计[J]. 传感技术学报,2010,23(1):78-81.

[9] 王平,许琴,范文政,等. 超声成像中基于特征空间前后向最小方差波束形成[J]. 声学学报,2013,38(1):65-70.

[10] 陈民铀,王伟明. 基于分段动态变迹技术的超声成像方法[J]. 重庆大学学报,2011,33(3):60-64.

[11] 彭虎. 超声成像算法导论[M]. 合肥:中国科技大学出版社,2008:114-116.

[12] Mishra A,Thakkar F,Modi C,el al. ECG Signal Compression Using Compressive Sensing and Wavelet Transform[C]//Engineering in Medicine and Biology Society(EMBC)Annual International Conference of the IEEE. San Diego,California,USA IEEE Press:2012,3404-3407.

[13] Lertsilp D,Umchid S,Techavipoo U. Resolution Improvements in Ultrasound Elastography Using Dynamic Focusing[C]//Biomedical Engineering International Conference(BMEiCON),Ubon Ratchathan,Thailand:IEEE Press,2012:1-4.

[14] 徐同伟,何庆,吴意乐,等. 基于自适应ABC/FOA融合定位算法研究[J]. 传感技术学报,2017,30(2):279-283.

[15] Wong L P,Chen A I,Logan A S,et al. An FPGA-Based Ultrasound Imaging System Using Capacitive Micromachined Ultrasonic Transducers[J]. IEEE Trans Ultrason Ferroelectr Freq Control,2012,59(7):1513-1520.

[16] Wang S L,Li P C. High Frame Rate Adaptive Imaging Using Coherence Factor Weighting and the MVDR Method[J]. IEEE Ultrasonics Symposium,2008,1175-1178.

[17] Mohammadzadeh A B,Ali M. Contrast Enhancement and Robustness Improvement of Adaptive Ultrasound Imaging Using Forward-Backward Minimum Variance Beamforming[J]. IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,2011,48(4):858-867.

[18] 江念,王召巴,陈友兴,等. 电磁超声检测钢板厚度实验的参数优化[J]. 传感技术学报,2015,28(4):498-502.