基于聚焦式超声波传感器的悬移质浓度测量研究*

夏一丹,谢代梁,安雅丽,王月兵

(中国计量大学,浙江省流量计量技术研究重点实验室,杭州 310018)

两相流现象广泛存在于石油开采、水利工程及航空航天等领域。原油含水率的确定[1]和水利建筑水下部分的维护[2]、液体混合的射流冲击[3]以及飞行器上蒸发循环制冷系统[4]等均属于两相流范畴。自然水体的流动过程中常常携带着大量的泥沙等颗粒物,为一种典型的液固两相流现象,其中固相颗粒被称为悬移质,其浓度和粒径等特性的深入研究对两相流的整体认识、流动情况的掌握以及两相中任意相的合理利用和对地理、生态环境影响的探索等有着重要意义。

最初的悬移质浓度和粒径的测量方法以直接法为主,总体上存在着效率低下、准确度不高、自动化程度低等大量缺陷。随着科技的不断发展,基于不同物理原理的间接测量法逐渐出现和完善。其中超声波测量法以其方向性好、无侵入、能量集中等优点得到人们的关注。利用超声波在不同浓度和粒径的悬移质溶液中传播时衰减程度不一样的超声波衰减法对悬移质浓度进行测量,已被证实具有自动化程度高、可以实时测量、对流体无影响的优势[5-6]。

近年来基于超声波衰减法的悬移质浓度测量探究和仪器的研制引起了国内外的重视。章维等[7]在低浓度条件下对聚苯乙烯-水悬浊液进行了超声实验,结合反演算法,证明了超声波衰减法在颗粒参数测量方面的可行性;Richard Challis等[8]考虑到超声波频率的影响,对不同浓度和粒径下的超声波衰减谱进行了分析,获得了相关测量模型并进行了不确定度分析。此外还有超声波信号的选取[9]、超声模型的优化[10]、测量原理的改进[11]等研究,为超声波衰减法的悬移质浓度测量提供了大量的理论基础和技术支持。

现有的研究已经涵盖了超声波的信号源种类、衰减谱的影响因素和获取途径、信号的处理方式等多个方面,但无不例外地采用了平面式超声波传感器,实际悬移质浓度测量中,测量结果与超声波传感器的种类特征、基本原理和精度密切相关。本文提出一种基于聚焦式超声波传感器的液固两相两相流测量方法,采用了新型的球形凹面聚焦式超声波传感器对3种不同平均粒径的悬移质溶液进行实验,结合小波变换和快速傅里叶变换[12-13]等手段得到衰减系数值,建立了不同粒径下与衰减系数相关的浓度测量模型,并进行了误差分析。

1 超声衰减测量原理

超声波在固液混合介质中传播时根据固相颗粒的大小、浓度等参数的不同产生不同角度的反射和折射,宏观上体现为经过介质的超声波的能量的衰减。引起声波衰减的原因按机理来分一般有3类:吸收衰减、散射衰减和扩散衰减。在已知固相颗粒的特性参数和连续相介质的性质情况下可以通过公式计算得到三大类衰减相应的衰减系数。实际上,完整获得相关参数的具体数值相当困难,直接计算得到衰减系数是不可行的,故从衰减系数的定义出发,以超声波的幅值为切入点,根据声呐方程,在超声波实验中接收波形的衰减系数按式(1)计算。

(1)

式中:α为声衰减系数,Vl和V0分别为悬浊液中和清水中接收信号的幅值,L为声程。

超声波在悬浊液中多次反射后,在接收传感器端会形成多次回波,衰减损失表现为接收信号幅值逐级递减,测量原理如图1所示。分别提取多次回波各自的衰减系数,取其平均值作为单次实验的衰减系数。

2 小波去噪原理

小波变换具有多尺度分析的特点,能够准确的区分出信号的高频部分和低频部分。原始的接收信号经过小波变换被分解成了不同的频率信号的叠加,信号有用部分和噪声分别集中在信号不同频率层,在选取合适的阈值情况下可以有效地提取有用信号以供后续研究[14]。在回波信号采集过程中,信号夹杂着随机噪声和白噪声,单纯的利用多次采集求平均值无法获取高信噪比的衰减信号。结合噪声的特点,引入自适应小波算法对衰减信号进行去噪处理。

小波变换的去噪过程主要包括原始信号的预处理、分解层数的确定、高频部分的阈值量化和信号的重构[15]。

如图2所示,衰减信号按照小波分解树逐层分解,每一层包括一个近似分量Ai和细节分量Di,在更高一级分解中,将Ai分解为频率更低的Ai+1和Di+1直至分解到设定的分解层数,Ai只包含低频成分,而Di包含高频成分,选择合适的阈值对细节分量Di的小波系数βi进行处理,减小噪声的小波系数,再把调整后的小波系数进行重构,去噪后的信号为如式(2)所示[16-19]:

(2)

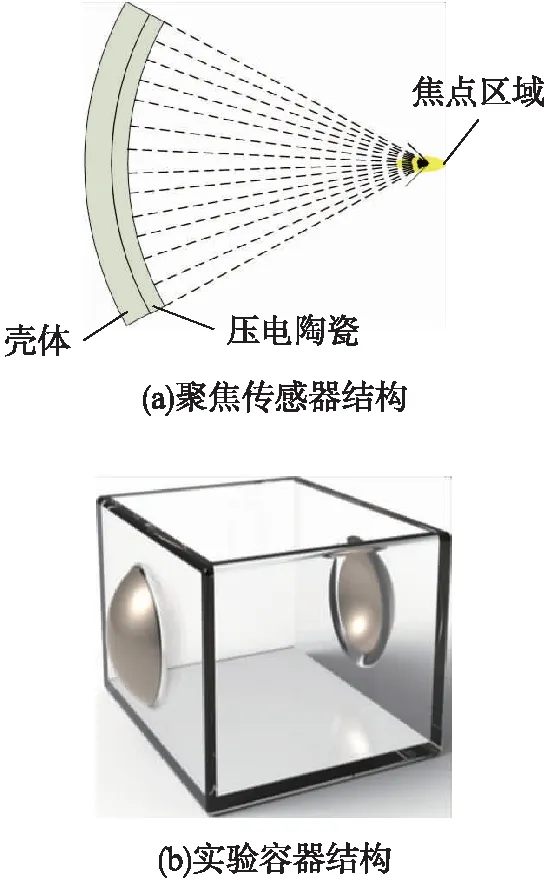
图3 聚焦超声传感器

3 实验装置

3.1 聚焦超声传感器

与传统平面传感器相比,聚焦传感器最大的特点是大大减小了超声波在传播过程中的散射衰减[20-21],具有散射损失小、灵敏度高等优点。其结构如图3(a),由壳体和凹面压电陶瓷片组成,在工作过程中超声波在空间某处声强最大,为聚焦传感器的焦点。聚焦式超声波发射传感器按照设置发射出周期性猝发波,在悬移质溶液中传播时在颗粒表面改变传播方向而发生了相对的衰减,导致接收传感器接收的声能减小,信号的幅值减小。由于聚焦式超声波传感器的凹面设计,发射出的超声波束的传播方向集中于焦点,传播过程中的散射衰减大大削弱,有利于超声波信号的提取。

超声波传感器的安装方式主要为自发自收式和一发一收式,相对的,一发一收式可捕获的回波数量比自发自收式的少,但衰减程度较大,同时,产生的杂波要少,故实验采用一发一收式,超声发射和接收探头分别封装于有机玻璃容器中,尺寸为56 cm×28 cm×34 cm,如图3(b)。玻璃水槽内部又添置一个用声阻抗与水相似的材料制作的高透明度的二次容器,以防固相颗粒在搅拌过程中损伤超声波探头。

3.2 实验系统

实验系统流程示意图如图4,主要由三部分构成:信号发生模块,包括信号发生器和功率放大器;测量模块,包括超声波发射、接收传感器;数据采集模块,包括数据采集卡及PC终端。

图4 实验系统流程

实验信号发生器发出信号为频率为1.13 MHz的猝发波,幅值为2Vpp,功率放大器JYH-1000M,放大倍数为2.5倍,采集卡采样频率为5 MHz,单次采样点为7 000个,二次容器中悬移质水样总体积3 m3。

4 实验过程及数据分析

4.1 衰减信号的预处理

对粒径为0.117 mm、0.087 mm、0.062 mm的3种不同粒径的情况下的回波信号分别使用小波db10进行一到三级的小波变换,采用“ddencmp”函数在默认全局阈值的基础下进行去噪,经过试验发现3种粒径下的分解情况一致,经过三级小波变换分解后的回波信号图像已经去除大部分的噪声干扰,细节方面得到较好的还原。此外,更高级的分解层数会导致有效信号的削弱,引起波形失真。因此在本课题实验条件下,选用三级小波分解作为信号去噪的最佳分解层数。

经过尺度是3的小波分解,提取3种不同粒径下的近似系数和细节系数,重构衰减信号。不同粒径衰减信号分解后的近似分量和细节分量的具体结果如图5、图7和图9所示。其中近似分量代表着实验的噪声部分,它们的频率相对较低,变化无规律且没有幅度较大的尖峰,幅值仅在小范围内(10-3数量级)波动。3种粒径对应衰减信号去噪前后对比结果如图6、图8和图10所示。

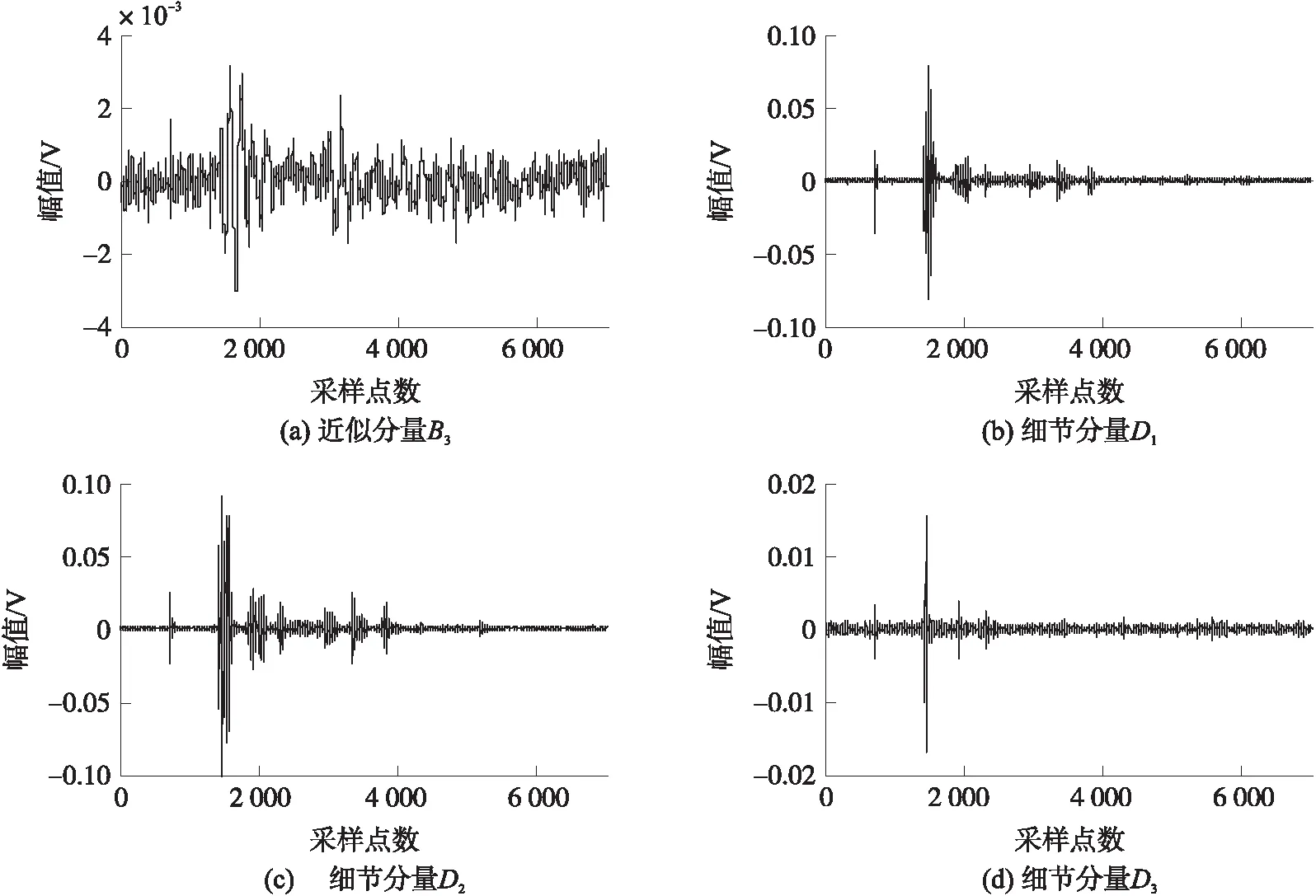
图5 R=0.117 mm小波分解系数示意图

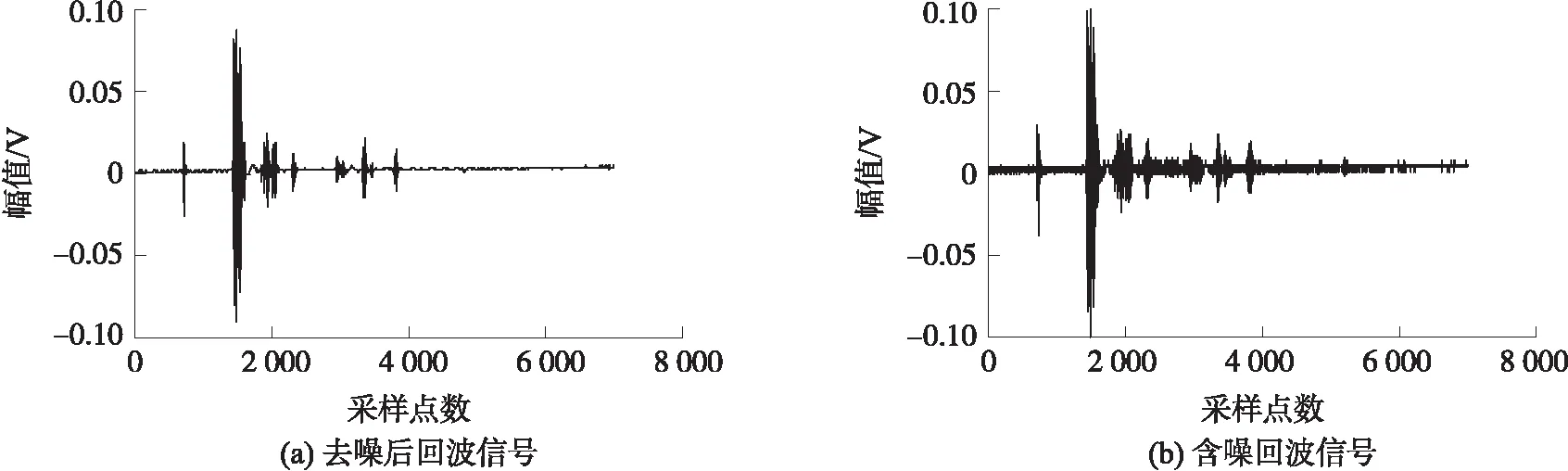
图6 R=0.117 mm衰减信号去噪前后对比图

图7 R=0.087 mm小波分解系数示意图

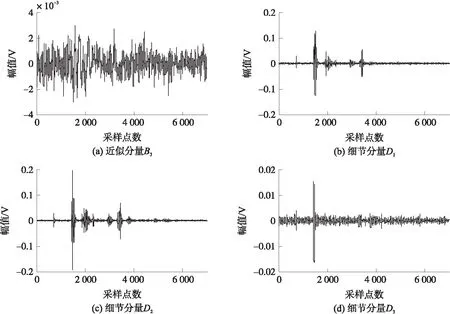
图9 R=0.062 mm小波分解系数示意

图10 R=0.062 mm衰减信号去噪前后对比图

从图中可以看出,一方面3个回波信号被清晰完整地还原出来,另一方面去噪后的信号幅值在无回波时候在0值点左右,整个回波信号相对含噪回波信号更加清晰简洁,去噪效果明显。经过信号重构,得到的衰减信号更加接近理论衰减信号,有益于后续的幅值提取和衰减系数计算。

4.2 声衰减系数测量

原始发射信号、清水中衰减信号、二次容器加清水衰减信号和悬浊液衰减信号时域波形如图11所示,波形依次出现了明显的衰减现象。由清水回波信号图可见,一次和二次回波非常明显,隐约可以看到三次回波,四次以后的回波几乎看不到,为了获得更完整的衰减系数,将前三次回波均计入计算,采用三次回波中各自衰减系数的平均作为实验衰减系数。由二次容器加清水图可见在加入二次容器后出现了由壁面多次反射造成的杂波,此时根据清水中的回波信号位置可以获得三次回波分别对应的时间点,挑选出所需一、二、三次回波位置,并对其进行小波去噪及FFT变换。

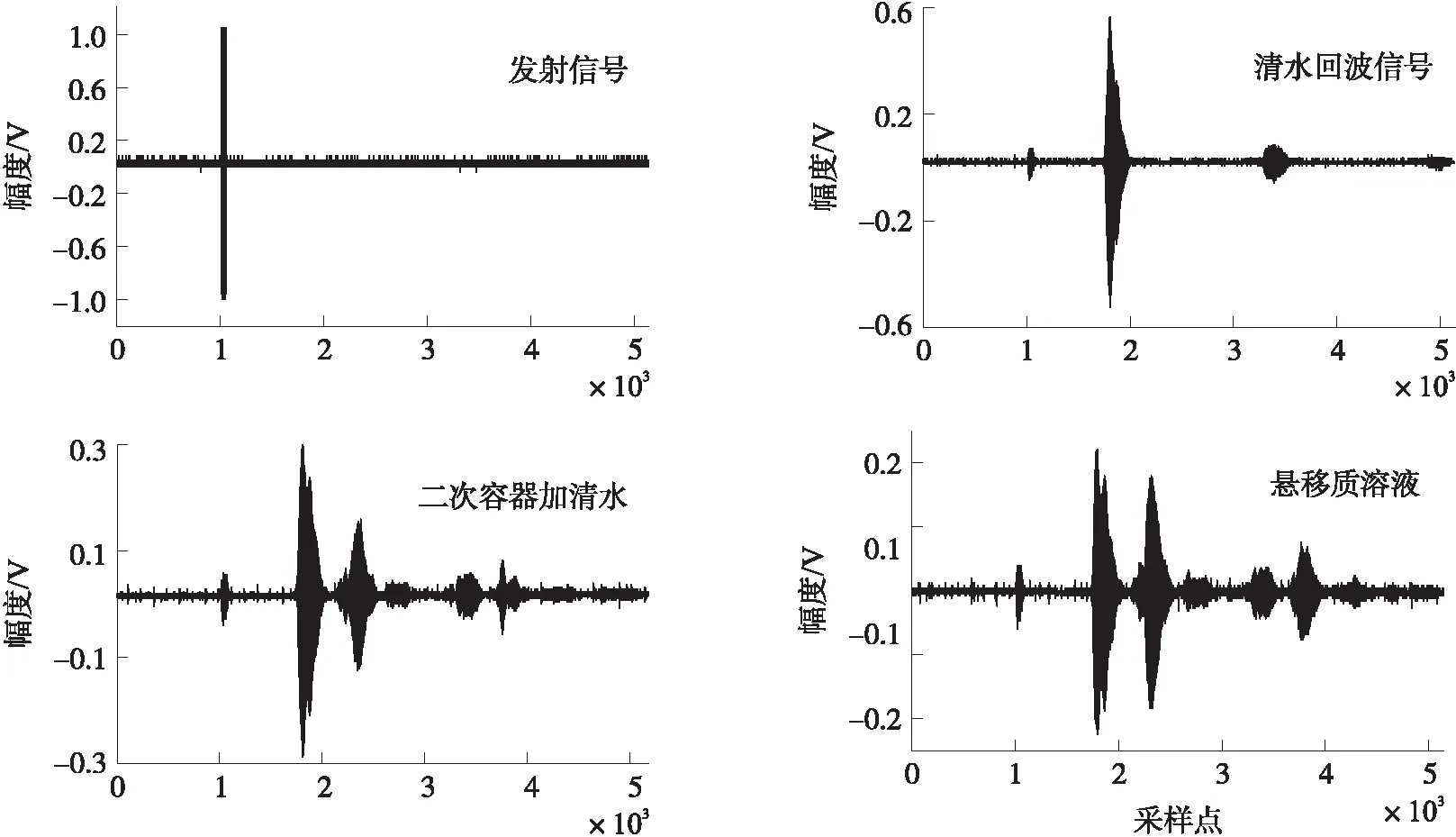
图11 不同条件下衰减波形对比

一、二、三次回波频谱图如图12所示。理论上超声波在各个频率下的衰减均可得到对应的衰减系数,但传感器在其中心频率下工作时衰减更为明显,故选取1.13 MHz作为工作频率。从频谱图上可见,超声波能量集中在工作频率附近,但其他频率也有少量能量分布,获得三次回波在工作频率下的幅值即可通过式(1)计算得出衰减系数。

4.3 混合粒径下浓度-衰减系数分布规律

在室温下对钱塘江悬移质水样进行实验,衰减系数值由式(1)得到,参考浓度值由烘干法得到,通过对实验衰减系数和参考浓度值进行多项式拟合的方式得到拟合式(3),并绘制浓度-衰减关系图，如图13所示。从多项式拟合式(3)可以看出衰减系数随浓度增大呈先增后减再增的过程。根据已知理论,低浓度时衰减系数与浓度为线性关系,但由于实验水样粒径分布未知,搅拌时流动情况复杂,线性关系无法适用于实验分布规律。

α=0.809 4φ3-4.996 6φ2+8.978 9φ+12.055

(3)

式中:φ为悬移质溶液浓度。

4.4 不同粒径下浓度-衰减系数分布规律

考虑到粒径大小对浓度-衰减系数关系的影响,使用分样筛将烘干后的悬移质按粒径大小进行分类,配制平均粒径分别为0.117 mm、0.087 mm和0.062 mm的悬移质水样后进行实验,其分布关系如图14所示。

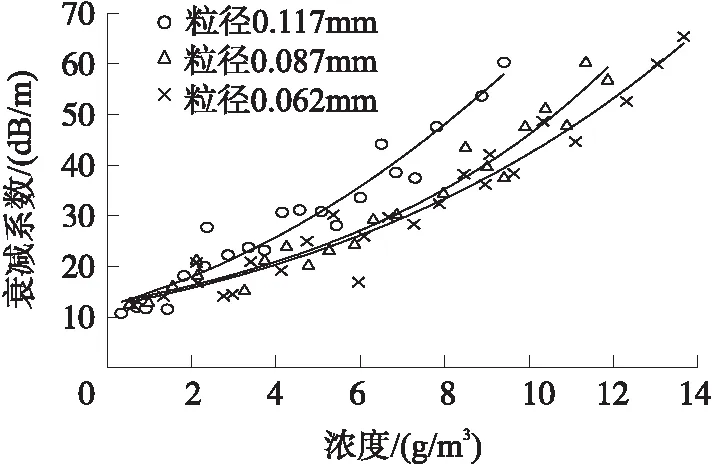
图14 不同粒径下浓度与衰减系数关系图

图14中可以看出,不同平均粒度下的浓度与衰减系数呈较好的幂函数分布规律,通过拟合式(4)和拟合系数表1建立悬移质浓度测量模型并进行误差分析如图15所示,在实验范围内,不同粒径的相对误差随浓度增大而减小,平均相对误差和均方根误差如表2所示。

α=e(aφ2+bφ+c)

(4)

式中:a、b、c分别为拟合系数。

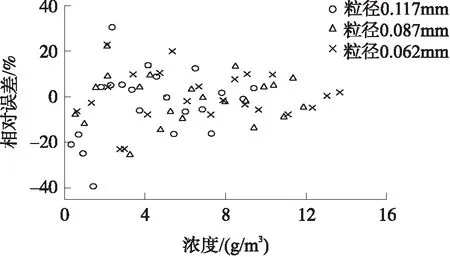
图15 不同粒径下浓度模型误差分布图

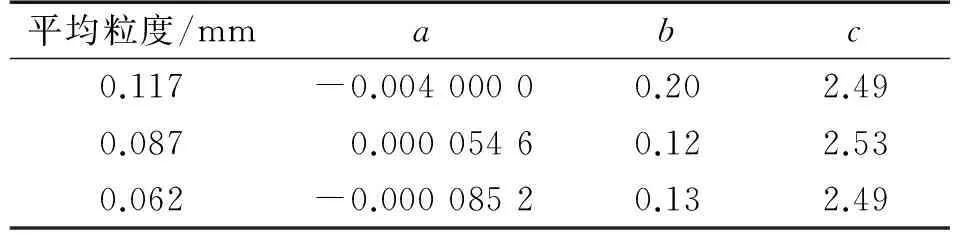
平均粒度/mmabc0.117-0.00400000.202.490.0870.00005460.122.530.062-0.00008520.132.49

值得提出的是,整体上悬移质浓度与衰减系数为幂函数关系不变的情况下,不同的平均粒径会导致拟合系数的改变,故实际测量中,只要是单一粒径情况,利用拟合式(4)采取实验方法对拟合系数进行修正即可。另一方面,前人已经验证了平面式超声探头下高浓度悬移质测量的可行性,可以弥补现今广泛使用的光学测量方法的不足,理论上采用聚焦式传感器同样可以用于测量高浓度的悬移质浓度测量,本次实验因为器材限制仅完成了低浓度情况的实验,高浓度测量有待后续研究。

表2 不同粒径下浓度模型误差

5 结论

本文利用聚焦超声衰减法对粒径分别为0.117 mm、0.087 mm、0.062 mm的悬移质溶液进行相关实验,建立了不同粒径条件下衰减系数与浓度的分布模型。在实验范围内,其平均相对误差分别为3.058%、1.057%、0.271%,均方根误差分别为9.201%、8.210%和6.686%,该模型为测量悬移质溶液浓度提供了一种有效方法。

[1] 高国旺,李利品,党瑞荣,等. 电导法原油含水率测量传感器的模型优化与仿真[J]. 传感技术学报,2015,28(9):1307-1314.

[2] 周国全,孙东振,彭获然. 基于LabVIEW平台的新型二维微位移传感器设计[J]. 传感技术学报,2015,28(4):607-612.

[3] 王兴涛,田芳,Jascha,等. 基于线列阵传感器的射流冲击试验含气率分布研究[J]. 传感技术学报,2015,28(7):1008-1015.

[4] 祝薇,邓元,王瑶,高洪利,等. 热电薄膜材料的制备和制冷器件的数值模拟[J]. 北京航空航天大学学报,2015,41(8):1435-1442.

[5] Thorne P D,Hardcastle P J. Acoustic Measurements of Suspended Sediments in Turbulent Currents and Comparison with in-situ Samples[J]. Journal of the Acoustical Society of America,1997,101(5):2603-2614.

[6] Thosteson E D,Hanes D M. A Simplified Method for Determining Sediment Size and Concentration from Multiple Frequency Acoustic Backscatter Measurements[J]. Journal of the Acoustical Society of America,1998,104(2):820-830.

[7] 章维,苏明旭,蔡小舒. 基于超声衰减谱和相速度的颗粒粒径测量[J]. 化工学报,2014,65(3):898-904.

[8] Allashi R S,Challis R E. Uncertainties in Ultrasonic Particle Sizing in Solid-In-Liquid Suspensions[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control,2014,61(11):1835-45.

[9] Wang X,Su M X,Cai X S. Effects of Material Viscosity on Particle Sizing by Ultrasonic Attenuation Spectroscopy[J]. Procedia Engineering,2015,102:256-264.

[10] Su M,Xue M,Cai X,et al. Particle Size Characterization by Ultrasonic Attenuation Spectra[J]. Particuology,2008,6(4):276-281.

[11] Weser R,Wöckel S,Wessely B,et al. Particle Haracterization in Highly Concentrated Dispersions Using Ultrasonic Backscattering Method[J]. Ultrasonics,2013,53(3):706-716.

[12] 苏玉刚,徐思文,吕志坤,等. 基于频域分离解调的复合信源无线电能与信号并行传输技术[J]. 电力系统自动化,2017(2):53-59.

[13] 张浪,侯志强,余旺盛,等. 利用快速傅里叶变换的双层搜索目标跟踪算法[J]. 西安电子科技大学学报,2016(5):153-159.

[14] 刘瑾,黄健,叶德超,等. 旋转叶片振动信号的小波变换去噪处理[J]. 纳米技术与精密工程,2016(2):100-105.

[15] 马敏,张彩霞,陆成超,等. 基于小波变换的ECT图像处理[J]. 中南大学学报(自然科学版),2016(6):1947-1952.

[16] 余倩,李跃忠. 基于小波变换的超声波含噪信号处理[J]. 电子质量,2013(11):14-18.

[17] Florindo J B,Bruno O M. Texture Analysis by Fractal Descriptors over the Wavelet Domain Using a Best Basis Decomposition[J]. Physica A Statistical Mechanics and Its Applications,2015,444:415-427.

[18] 周知进,文泽军,卜英勇. 小波降噪在超声回波信号处理中的应用[J]. 仪器仪表学报,2009(2):237-241.

[19] 石海信,王爱荣,闭梅,等. 微波辐射淀粉热重试验及其数据的小波去噪处理[J]. 中国粮油学报,2016(5):49-55.

[20] 戚萌,王鑫,刘晓宙. 大张角聚焦传感器中的张角变化对生物组织温度场的影响[J]. 南京大学学报(自然科学),2017(1):114-121.

[21] Chung C H,Lee Y C. Fabrication of Poly(Vinylidene Fluoride-Trifluoroethylene)Ultrasound Focusing Transducers and Measurements of Elastic Constants of Thin Plates[J]. NDT & E International,2010,43(2):96-105.