无线传感器网络中的线性移动目标运动参数捕获方法*

吴晓平,华宇婷,胡军国,2,王国英

(1.浙江农林大学信息工程学院,浙江 临安311300;2.浙江省林业智能监测与信息技术研究重点实验室,浙江 临安 311300)

通过节点间的传感信息交换与收集,实现对移动目标位置的估计与预测,即移动目标跟踪是无线传感器网络的重要应用方向[1-2]。比如,在军事环境下对特定目标的跟踪,动物生活习性的监测以及交通应用中的移动目标跟踪等都可以采用无线传感器网络来实现。通过无线传感器网络中移动节点与它节点间的信号测量、采样与数据收集,以确定移动节点的运动路径与参数,即移动目标跟踪亦具有重要的研究价值。在大量关于无线传感器网络移动目标跟踪的研究中,研究人员重点关注如何精确快速地获取移动目标位置与运动参数[3-4]、如何实现高效地数据收集以及节省能量和通信开销[5]。

移动目标跟踪的重要内容就是估计移动目标的当前位置参数或预测将来的位置参数[6-7]。为获取当前位置参数即定位目标位置坐标,通常需要测量节点间距离,再利用定位算法估算移动目标的位置。常用的节点间距离测量方法包括到达时间(TOA)[8]、到达时间差(TDOA)、到达角度(AOA)[9]与信号接收强度(RSS)[10-11]等。根据建立的节点间距离约束方程,已有的定位算法包括极大似然(ML)估计法、最小二乘线性代数法[12-13]及凸优化算法[14]等。ML估计法一般采用数值计算方法估计,但数值计算方法严重依赖于初始解,若初始解选择不合适,有可能导致局部最优,为此提出了最小二乘线性代数法及凸优化算法。最小二乘线性代数法将计算结果直接表示为代数解,计算过程较快。凸优化算法中常见的主要为半正定规划(SDP)算法,SDP算法将非凸优化模型松弛为凸优化模型,具有较多的变量和等式约束,计算复杂度较高,但算法稳定性较好。

移动目标的位置估计对于事件监测、辅助定位及覆盖控制等都具有重要意义,也是移动无线传感器网络的重要内容[15]。常用的移动目标位置估计方法包括卡尔曼(KF)滤波[16]、扩展卡尔曼(EKF)滤波以及粒子(PF)滤波[17]等。当观测方程存在高斯噪声时,KF滤波通过不断的预测与校正更新估计值,以提高移动目标的跟踪精度,但KF滤波只适用于线性运动与观测方程。为将预测模型应用于非线性方程,EKF滤波对非线性方程进行线性化,传统的KF滤波应用范围进一步扩大。但KF滤波及EKF滤波只能用于高斯噪声的处理,为此提出了PF滤波,通过不断地重采样方法实现对目标位置的预测与更新。

采用节点间的TOA测量方法,本文介绍了一种无线传感器网络中移动目标的运动参数捕获方法。假设移动目标的线性移动模型,通过移动节点与信标节点间的TOA测量,建立了移动目标运动参数的优化估计模型。根据建立的运动参数优化估计模型,推导了线性移动目标初始位置及移动速度的非约束线性最小二乘(ULLS)和约束线性最小二乘(CLLS)方法。将估计模型松弛为凸优化的SDP问题,提出了运动参数捕获的SDP算法。通过对算法的仿真实现与分析,进行了各算法的性能比较,分析了采样周期及采样点数量对捕获精度的影响。

本文第1部分首先线性移动目标与信标节点间测量的问题描述;第2部分推导了ULLS和CLLS的代数计算方法;第3部分提出了估计模型的SDP算法;第4部分问题模型的克拉美罗(CRLB)下界值;第5部分为仿真分析;最后部分为结论。

1 问题描述

假设在二维平面(三维空间的分析方法同二维平面)上分布着M个已知位置坐标的信标节点,其坐标位置分别为xi=[xiyi]T,(i=1,2,…,M)。同时在该区域上有一移动目标节点从初始位置x0=[x0y0]T出发,以速度ν=[νxνy]T恒定速度保持匀速直线移动,如图1所示。

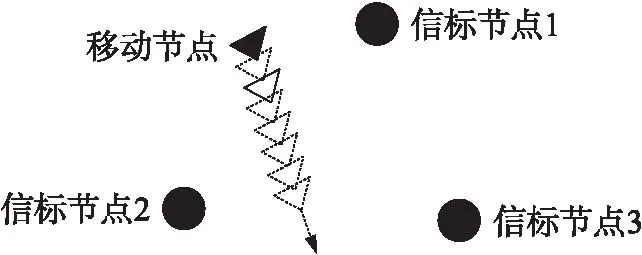
图1 移动节点与信标节点的位置分布示意图

移动节点从初始位置x0以恒速ν直线移动,同时以采样周期T间隔测量与各信标节点间的TOA到达时间,并将此表示为ti,n,有以下关系式

(1)

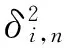
di,n=‖xi-x0-nTν‖

(2)

将式(2)代入式(1),可表示为

(3)

式中:n=0,1,2,…,N,i=1,2,…,M。令en=[1nT]T,可将式(3)进一步表示为

(4)

(5)

所建立优化方程(5)的目标是精确地估计出移动节点的初始位置x0及移动速度ν。为求解上述未知向量,可以采用数值计算方法。但数值计算方法有可能陷入局部最优,本文下面分别介绍线性代数法及凸优化算法的实现过程。

2 线性代数法

为获取移动目标的位置及运动参数,本节介绍将优化方程(5)转化为最小二乘估计问题,分别设计了非约束线性最小二乘法及约束线性最小二乘估计法。

2.1 非约束线性最小二乘法

线性代数法直接将估计值表示为代数形式解析解,计算过程较快。为得到优化方程的代数解,先对式(3)进行等效变换,重新表示为

‖xi-μTen‖=c(ti,n-εi,n)

(6)

对式(5)两边平方,考虑噪声εi,n的较小波动范围,忽略二次高阶项,可以得到

(7)

式中:n=0,1,2,…,N,i=1,2,…,M。由于en=[1nT]T,将μ=[x0ν]T代入式(7),可重新表示为

(8)

Aη=b+α

(9)

根据线性最小二乘平方原理,未知向量η的估计值为

(10)

式中:维度为M(N+1)×M(N+1)的权重矩阵Σα=E(αTα),其值表示为

(11)

假设未知向量η的估计误差为Δη,其值表示为

(12)

将估计误差Δη的方差表示为cov(Δη),有

(13)

2.2 约束线性最小二乘法

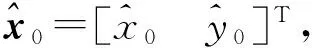
(14)

式中:η(k)、Δη(k)表示了向量η、Δη的第k个元素,k=1,2,…,6。可将式(14)表示为线性矩阵形式

Gu=h+γ

(15)

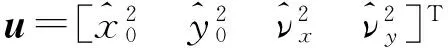
(16)

同样利用线性最小二乘平方原理,向量u的无偏估计表示为

(17)

式中:维度为6×6的权重矩阵Σγ值为

(18)

(19)

将以式(19)表示的计算过程考虑了向量η中元素间的相互约束关系,得到了更为精确的估计结果,将此计算方法称为移动节点参数捕获问题的约束线性最小二乘(CLLS)方法。

3 凸优化SDP算法

SDP算法将建立的式(5)所描述的非凸优化模型松弛为凸优化问题。将式(1)重新整理,公式两边平方,忽略二次高阶项,有关系式

(20)

结合式(20)及式(2),亦可将优化问题表示为如下形式

(21)

为将式(21)松弛为凸优化形式,定义未知矩阵Z,表示为

(22)

式中:Y=[x0ν]。不难发现有如下关系式

(23)

进一步松弛Z为半正定矩阵,即Z≥04,再对式(21)作进一步等效变换为以下凸优化问题

(24)

根据矩阵Z的定义,可从Z抽取出移动节点的初始位置x0及移动速度ν估计值。

4 克拉美罗下界值

克拉美罗下界值(CRLB)为模型待估参数的无偏估计提供了误差方差的下界。考虑问题模型中的待估计向量μ=[x0ν]T,根据克拉美罗下界理论,有关系式cov(μ)≥F-1,这里cov(μ)表示了未知向量μ的估计误差方差,F为待估计向量μ的FIM(Fisher Information Matrix)的表示,可表示为

(25)

式中:P(p|x)为概率密度函数,可以表示为

(26)

lnP(p|μ)=λ-ρTΣ-1ρ

(27)

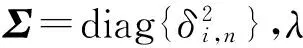
将式(27)代入式(25)展开,矩阵F可表示为

(28)

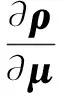
(29)

对式(29)进一步求解展开,得到如下关系式,

(30)

则根据CRLB无偏估计下界理论有

(31)

式中:[F-1]r,r表示F的逆矩阵的第r行、第r列元素值,r=1,2,3,4;CRLB(x0)、CRLB(ν)分别表示了初始位置x0及移动速度ν的CRLB无偏估计下界值。

5 仿真分析

采用线性移动目标与信标节点间的TOA测量方法,本文提出了线性移动目标的初始位置坐标及移动速度估计模型,并设计了模型的ULLS、CLLS及SDP计算方法。为验证与比较各算法的计算性能,采用MATLAB 软件进行了算法的仿真实现。在100 m×100 m的方形区域内设置4个信标节点位置坐标在(80,65),(90,10),(15,20),(10,55),并随机生成10个移动节点的初始位置。同时将移动节点的x轴方向移动速度νx及y轴方向移动速度νy都预先设置为1 m/s,信号传播速度c设置为3×108m/s,所有的时间测量噪声εi,n的噪声方差均设置为δ2。为衡量所设计算法的估计误差,采用均方根误差(RMSE)分析。对每种算法的RMSE估计误差仿真运行1 000次,采用1000次运行结果的平均值分析。

5.1 时间测量噪声对估计误差的影响

设置采样周期T为1 s,采样点N等于20,同时调整时间测量噪声δ从1 ns到10 ns之间变化,图2绘出了不同算法的RMSE估计误差随时间测量噪声变化关系。图2(a)中,CWLS方法曲线的为文献[13]所提出的静止节点(即采样点数量N等于零时)位置估计误差。由图2(a)可见,当时间测量噪声δ为10 ns时,ULLS、CLLS、SDP及CWLS算法的初始位置RMSE估计误差分别为1.92 m、1.58 m、1.70 m及3.32 m,本文所提出的3种算法的估计误差都远小于静止节点的CWLS方法。对比本文提出的3种算法,ULLS算法的初始位置估计误差最大,凸优化SDP算法其次,CLLS算法的位置估计误差最小。显然,随着时间测量噪声δ的增大,3种算法的初始位置RMSE估计误差也随之增大。比如,当时间测量噪声δ设置在1 ns时,ULLS算法的RMSE位置估计误差为0.19 m;而当时间测量噪声δ增加到10 ns时,ULLS算法的RMSE位置估计误差也上升到了1.92 m。

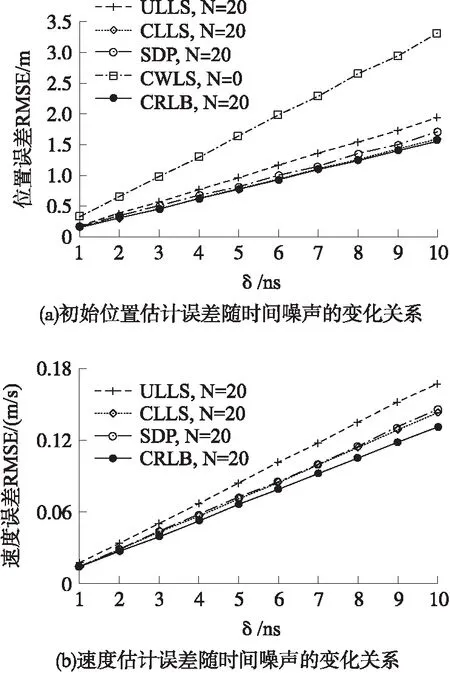
图2 时间测量噪声对估计误差的影响

移动节点的移动速度与初始位置坐标同时被估计,图2(b)绘出了本文提出3种不同算法的RMSE速度估计误差随时间测量噪声的变化关系。同图2(a)一样的结果发现,ULLS、CLLS及SDP 3种算法的估计误差随时间测量噪声的增加而增大。当时间测量噪声δ设置在1 ns时,ULLS算法的RMSE速度估计误差为0.017 m/s;而当时间测量噪声δ增加到10 ns时,ULLS算法的RMSE速度估计误差也增大到了0.167 m/s,估计误差近似与时间测量噪声成线性增加关系。相比于图2(a),ULLS、CLLS及SDP 3种算法的估计误差性能排列顺序没有变化,ULLS算法的RMSE速度估计误差最大,SDP算法其次,CLLS算法的RMSE速度估计误差最小。与图2(a)的分析结果不同之处在于CLLS算法的速度估计误差稍有所增大,更偏离于CRLB下界值。

5.2 采样周期对估计误差的影响

在实际系统应用中,采样周期T可随意设置,但采样周期T大小直接涉及到误差性能。保持时间测量噪声δ等于10 ns及采样点数量N等于20,仿真测试了不同采样周期T大小对估计误差的影响。当采样周期T从0.5 s增加到5 s时,图3(a)绘出了ULLS、CLLS及SDP 3种不同算法的初始位置RMSE估计误差随采样周期T的变化关系。由图3(a)可见,3种算法的位置RMSE误差随采样周期T的增加而稍有增大。当采样周期T等于0.5 s时,CLLS算法的RMSE位置估计误差为1.57 m;当采样周期T增加到5 s时,CLLS算法的RMSE位置估计误差也增加到了1.78 m。

图3 采样周期对估计误差的影响

采样周期T越小,对速度估计的影响更大,图3(b)绘出了ULLS、CLLS及SDP 3种算法的RMSE速度估计误差随采样周期的变化关系。由图3(b)可见,3种算法的速度误差都随着采样周期T的增大而减少。比如,当采样周期T等于0.5 s时,CLLS算法的RMSE速度估计误差为0.28 m/s;而当采样周期T达到5 s时,CLLS算法的RMSE速度估计误差仅为0.037 m/s。并且由图3(b)可以看出,RMSE速度估计误差与采样周期T有近似成反比关系,当采样周期T小于2 s时,RMSE速度估计误差尤其大。在实际应用中,增大采样周期T有助于减少速度估计误差,但同时将增加移动节点的运动距离,有可能导致运动距离过大而无法实现与移动节点间的TOA测量。

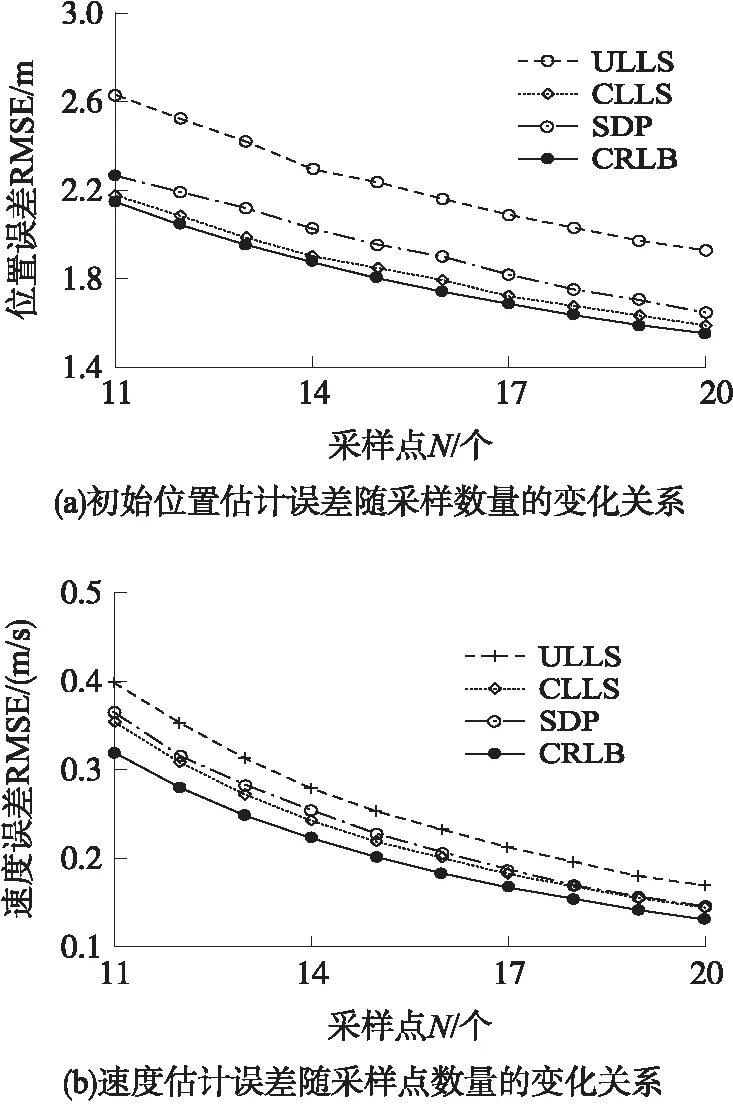
图4 采样点数量对估计误差的影响

5.3 采样点数量对估计误差的影响

随着采样点数量N的增加,所获取的测量信息更加多,各种算法的估计精度将进一步提高。保持采样周期T为1 s,时间测量噪声δ等于10 ns,仿真测试了不同采样点数量N下的估计误差性能,并将结果绘于图4。当采样点数量N从11到20之间变化时,图4(a)绘出了ULLS、CLLS及SDP 3种不同算法的RMSE位置估计误差随采样点数量N的变化关系。不难看出,随着采样点数量N的增加,RMSE位置估计误差有所减少。比如,当采样点数量N等于11时,CLLS算法的RMSE位置估计误差为2.18 m;而当采样点数量N增加到20时,CLLS算法的RMSE位置估计误差仅为1.59 m。同样地,ULLS与SDP算法的RMSE位置估计误差也随采样点数量N的增加而减少。比较3种不同算法的估计误差性能,也可以发现采用约束CLLS算法的位置误差RMSE值在3种算法中最小,更加接近于CRLB理论下界值。

同样将采样点数量N从11增加到20,图4(b)绘出了ULLS、CLLS及SDP 3种不同算法的速度误差RMSE随采样点数量N的变化关系。由图4(b)亦可以看出,随着采样点数量N的增加,RMSE速度估计误差却随之减少。当采样点数量N等于11时,ULLS、CLLS与SDP 3种算法的速度估计误差分别为0.39 m/s、0.35 m/s、0.36 m/s;而当采样点数量N增加到20时,ULLS算法的速度估计误差减少到了0.17 m/s,CLLS与SDP两种算法的速度估计误差都减少到了0.14 m/s。随着采样点数量N的增加,估计误差减少,精度有所提高。但测量成本有所增加,并且采样点数量的增加表明移动节点运动距离加长,亦有可能超出节点间的TOA测量范围。

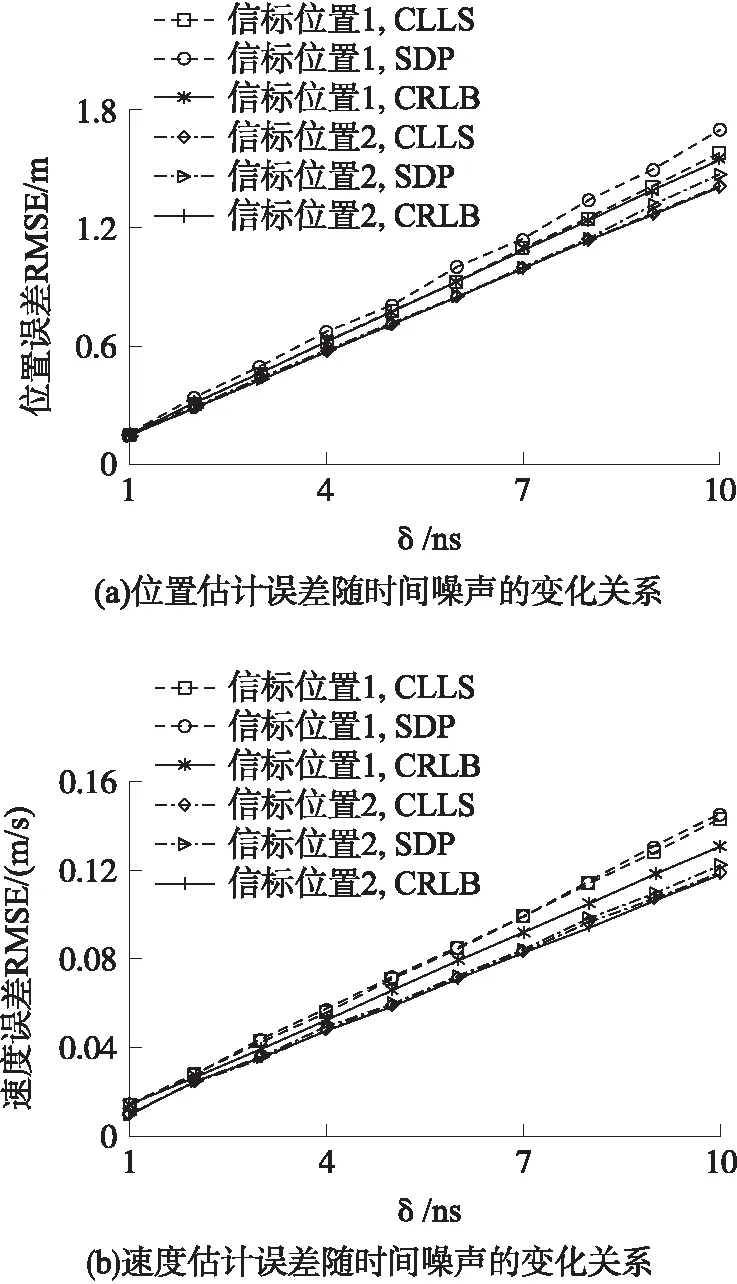
图5 信标节点位置对估计误差的影响

5.4 信标位置对估计误差的影响

信标节点位置亦直接影响位置及速度估计误差,如文献[18-19]所提出的信标节点位置对误差的影响分析。当采样周期T设置为1 s,采样点数量N等于20,时间测量噪声δ从1 ns到10 ns之间变化时,仿真亦测试了两种不同信标节点位置对速度估计误差的影响。当4个信标节点设置在(80,65),(90,10),(15,20),(10,55)称为信标位置1,将4个信标节点均匀设置在(0,0),(0,100),(100,0),(100,100)称为信标位置2,图5绘出了两种不同信标节点位置下CLLS、SDP算法与CRLB的估计误差。由图5(a)可以看出,当信标节点处于均匀位置2时,CLLS、SDP算法与CRLB的位置误差都要小于位置1的RMSE误差值。如当δ为10 ns时,信标节点处于非均匀位置1时,CLLS算法的位置误差RMSE值为1.59 m;而当信标节点处于均匀分布位置2时,CLLS算法的初始位置误差RMSE值却降低到了1.41 m。

当信标节点分别处于位置1及位置2时,图5(b)绘出了CLLS、SDP算法与CRLB的速度误差RMSE与时间噪声间的变化关系。由图5(a)亦可以看出,当信标节点处于均匀位置2时,CLLS、SDP算法与CRLB的速度估计误差RMSE值都要小于非均匀位置1的误差估计值。比如当δ为10 ns时,信标节点处于非均匀位置1时,CLLS算法的速度误差RMSE值为0.142 m/s;而当信标节点处于均匀分布位置2时,CLLS算法的速度误差RMSE值降低到了0.119 m/s。

6 结论

采用移动节点与信标节点间的TOA测量方法,本文提出了移动节点运动参数的捕获方法,并设计了包括初始位置坐标及移动速度的ULLS、CLLS及SDP计算方法。ULLS算法估计误差在所设计的3种算法中最大,CLLS算法由于采用了约束条件,估计误差最小。凸优化的SDP算法估计误差介于ULLS、CLLS算法之间,但众所周知,凸优化SDP算法的计算复杂度远大于代数计算方法,但算法稳定性较好。仿真结果发现,随着采样周期T的增加,位置估计误差稍有增大,但速度估计误差却在减少。更多的采样点数量N有利于增加测量信息量,可以减少估计误差。在保持移动速度不变的情况下,增大采样周期T及采样点数量N意味着移动距离的延长,由于通信距离的限制有可能导致无法实现TOA测量。在实际应用中,如何选择采样周期T及采样点数量N直接关系到参数捕获精度,本文提出的方法与参数影响关系对于实际应用具有一定的指导意义。

[1] Enyang Xu,Zhi Ding,Soura Dasgupta. Target Tracking and Mobile Sensor Navigation in Wireless Sensor Networks[J]. IEEE Transactions on Mobile Computing,2013,12(1):177-186.

[2] Juan Pedro Dominguezdiag Morales,Antonio Riosdiag Navarro,Domínguezdiag Morales M,et al. Wireless Sensor Network for Wildlife Tracking and Behavior Classification of Animals in Doana[J]. IEEE Communications Letters,2016,20(12):2534-2537.

[3] 周伟,石为人,张洪德,等. 无线传感器网络的分布式目标跟踪研究[J]. 仪器仪表学报,2013,34(7):1485-1491.

[4] Efren Lopes Souza,Eduardo Freire Nakamura,Richard W Pazzi.Target Tracking for Sensor Networks:A Survey[J]. ACM Computing Surveys. 2016,49(2):1-35.

[5] Oualid Demigha,WaliddiagKhaled Hidouci,Toufik Ahmed. On Energy Efficiency in Collaborative Target Tracking in Wireless Sensor Network:A Review[J]. IEEE Communications Surveys and Tutorials,2013,15(3):1210-1222.

[6] Kan Zheng,Huijian Wang,Hang Li,et al. EnergydiagEfficient Localization and Tracking of Mobile Devices in Wireless Sensor Networks[J]. IEEE Transactions on Vehicular Technology,2017,66(3):2714-2726.

[7] 左现刚,张志霞,贾蒙. 基于分布式聚类的有向传感器网络移动目标跟踪算法研究[J]. 传感技术学报,2016,29(7):1096-1101.

[8] Hong Shen,Zhi Ding,Soura Dasgupta,et al. Multiple Source Localization in Wireless Sensor Networks Based on Time of Arrival Measurement[J]. IEEE Transactions on Signal Processing. 2014,62(8):1938-1949.

[9] Yue Wang,Ho K C. An Asymptotically Efficient Estimator in Closeddiag Form for 3diagD AOA Localization Using a Sensor Network[J]. IEEE Transactions on Wireless Communications,2015,14(12):6524-6535.

[10] Chen Liu,Dingyi Fang,Zhe Yang,Hongbo Jiang,et al. RSS DistributiondiagBased Passive Localization and Its Application in Sensor Networks[J]. IEEE Transactions on Wireless Communications. 2016,15(4):2883-2895.

[11] 袁鑫,吴晓平,王国英. 线性最小二乘法的RSSI定位精确计算方法[J]. 传感技术学报.2014,27(10):1412-1417.

[12] So H C,Lanxin Lin. Linear Least Squares Approach for Accurate Received Signal Strength Based Source Localization[J]. IEEE Transactions on Signal Processing,2011,59(8):4035-4040.

[13] Cheung K W,So H C,Ma W K,et al. A Constrained Least Squares Approach to Mobile Positioning:Algorithms and Optimality[J]. EURASIP Journal on Applied Signal Processing,2006:1-23.

[14] Robin Wentao Ouyang,Albert KaidiagSun Wong,ChindiagTau Lea. Received Signal StrengthdiagBased Wireless Localization via Semidefinite Programming:Noncooperative and Cooperative Schemes[J]. IEEE Transactions on Vehicular Technology,2010,59(3):1307-1318.

[15] Soheil Salari,Shahram Shahbazpanahi,Kemal Ozdemir. Mobilitydiag Aided Wireless Sensor Network Localization via Semidefinite Programming[J]. IEEE Transactions on Wireless Communications,2013,12(12):5966-5978.

[16] Yihua Yu. ConsensusdiagBased Distributed Mixture Kalman Filter for Maneuvering Target Tracking in Wireless Sensor Networks[J]. IEEE Transactions on Vehicular Technology,2016,65(10):8669-8681.

[17] Qinghua Gao,Jie Wang,Minglu Jin,et al. Target Tracking by Lightweight Blind Particle Filter in Wireless Sensor Networks[J]. Wireless Communications and Mobile Computing,2014,14(2):210-220.

[18] Sheng Xu,Kutluyil Dogancay. Optimal Sensor Placement for 3diagD AnglediagofdiagArrival Target Localization[J]. IEEE Transactions on Aerospace and Electronic Systems,2017,53(3):1196-1211.

[19] Nikhil Bhagwat,Bijan Jabbari. Analysis of Localization Accuracy in Wireless Networks in Presence of Uncertain Beacon Positions[C]//GLOBECOM 2010:1-5.