基于AP聚类RBF神经网络的改进算法及试验*

刘小锋,冯志敏*,陈跃华,张 刚,李宏伟

(1.宁波大学海运学院,浙江 宁波 315211;2.宁波杉工智能安全科技股份有限公司,浙江 宁波 315100)

近年来,我国跨海、跨江大桥持续建设,高速公路网络体系逐步完善,然而车辆超限超载现象十分严重,对公路桥梁寿命造成影响,交通事故屡有发生,给人们生命财产和桥梁安全带来极大危害。车辆动态称重系统是快速检测超载车辆的一种有效方法,基于压电薄膜检测的车辆动态称重方法在工程上得到广泛应用[1-4],其中检测信号处理中径向基函数RBF(Radical Basis Function)神经网络算法对于提高车辆动态称重精度相当重要,受到学者广泛关注。RBF神经网络隐含层节点数、径向基函数中心、径向基函数宽度、连接权值等均影响着网络精度,大都通过K均值、模糊C均值、蚁群等聚类算法确定相关参数[5-7],提高了RBF神经网络精度。Frey[8]等人提出AP(Affinity Propagation)聚类算法,较其他聚类算法,不需事先设定聚类数和对聚类中心作初始化选择,可快速处理大规模数据。AP算法的偏向参数决定聚类数目,通常以相似度矩阵中值法、粒子群法、密度法等算法加以确定[9-11],一定程度上提高了AP算法聚类精度。但是,如何寻求一种确定偏向参数的优化算法以进一步提高RBF神经网络精度还需研究;另外,RBF神经网络训练完成后,由于连接权值固定不变,则RBF神经网络将难以对每一测试样本均达到较高精度。为使连接权值能自适应调整,递推最小二乘法、基于Lyapunov理论法已应用于RBF神经网络[12-13],其分别在网络结构确定、设计特定自适应控制律条件下取得较好效果,因此,RBF神经网络连接权值自适应调整算法仍需作进一步研究。

本文提出取相似度矩阵中值2倍为偏向参数初始值,按一定步长迭代增加偏向参数,以RBF神经网络测试误差为评价指标最终确定偏向参数的改进算法;提出将测试样本归类至经AP算法聚类后的训练样本集,在测试样本所在类集中,选取两个与测试样本至类代表点距离相差最小的训练样本,根据其实际连接权值,插值计算测试样本连接权值,实现连接权值的自适应调整;并且对该改进算法进行3种车型的工程实测试验,在车速10 km/h～50 km/h,温度16 ℃～29 ℃时,构建RBF神经网络车辆动态称重模型,对其进行500次循环测试,称重误差均值均控制在0.06%以内,最大实时性均值为0.022 3,网络结构简单、可靠。该算法适合交通和海洋工程结构振动信号的检测应用。

1 算法原理

1.1 AP聚类算法

设数据集X={xi,i=1,2,…,n},AP算法[8]将X中各数据点间负欧式距离平方称为相似度,即s(i,k)=-‖xi-xk‖2,取所有相似度构成n×n的相似度矩阵S,并将对角线元素s(k,k)称为偏向参数p,p越大,xk被选作类代表点的几率就越大,相应聚类数也就越多。由于每个数据点都有可能成为类代表点,故AP算法将p设为同一值,一般常取p为相似度矩阵中值。另外,AP算法又定义r(i,k)和a(i,k)两个信息量参数,分别代表不同竞争目的。其中,r(i,k)是从xi向xk发送消息,表示xk作为类代表点时对xi的吸引度,而a(i,k)是从xk向xi发送消息,表示xi选择xk作为类代表点时对xk的归属度。显然,r(i,k)与a(i,k)之和越大,xk被选作类代表点的几率就越大。

AP算法以相似度矩阵S和偏向参数p作为输入,对r(i,k)、a(i,k)进行迭代运算,当出现r(k,k)+a(k,k)>0时,则将xk视为一个类代表点。取a(i,k)初始值为0,按式(1)计算r(i,k),即

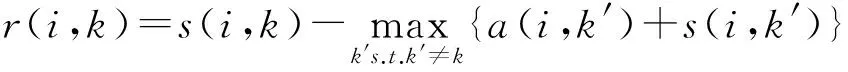
(1)

按式(2)计算a(i,k),即

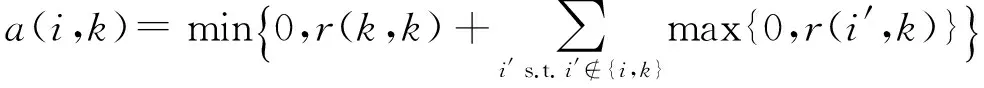
(2)

按式(3)计算a(k,k),即

(3)

当迭代超过1 000次或经连续50次迭代类代表点都不发生改变时,则迭代终止,聚类结束。

1.2 RBF神经网络模型

RBF神经网络为一种前馈型网络,仅由输入层、隐含层、输出层三层组成[14],结构如图1所示。

图1 RBF神经网络结构图

图1中,xi=(xi1,xi2,…,xil)T为输入向量,其中i=1,2,…,n,n为输入向量个数、φ(‖xi-cj‖)为隐含层节点激活函数,其中j=1,2,…,r,r为隐含层节点数、W∈Rr×m为隐含层与输出层间权值矩阵、∑为输出层节点激活函数、yi=(yi1,yi2,…,yim)T为输出向量。

输出层各节点的输出表达式为:

(4)

式中:φ(‖xi-cj‖)一般采用高斯基函数,即

(5)

式中:cj为隐含层第j个节点中心,‖·‖为欧式距离,δj为第j个高斯基函数宽度。

设理想输出向量为oi,取误差函数

(6)

为性能指标,利用梯度下降或最小二乘法计算连接权值,以完成RBF神经网络训练。

1.3 AP聚类RBF神经网络原理

AP算法应用于RBF神经网络,主要用来求取隐含层相关参数[15],以确定RBF神经网络内部结构。隐含层相关参数的求取过程一般如下:

①对训练样本集X={xi,i=1,2,…,n}、xi∈Rl按式(7)进行归一化[16],得

(7)

②利用AP算法对X′中样本进行聚类,若共产生r个类代表点cj,j=1,2,…,r,则取隐含层节点数为r、隐含层各节点中心分别为c1、c2、…、cr。

③由隐含层各节点中心,按式(8)计算高斯基函数宽度,即

(8)

根据隐含层相关参数以及输入、输出向量,构建RBF神经网络,最后再对RBF神经网络进行训练、测试。

2 改进算法

2.1 偏向参数的寻优

对于RBF神经网络隐含层节点数,过少会降低网络泛化力,而过多又将导致网络过拟合[17]。由于AP算法中偏向参数p决定聚类数,故p值大小必将影响RBF神经网络精度。以往常取p为相似度矩阵中值,但可能会造成隐含层节点数取得不够合理,从而使RBF神经网络精度降低。因此,可以RBF神经网络测试精度为评价标准,确定偏向参数。

偏向参数p为负值,其值越小,聚类数就越少,而当p取相似度矩阵中值2倍时,聚类数已很少。因此,可以在p为负值的条件下,从2倍相似度矩阵中值开始,迭代增加p值,取RBF神经网络测试误差达最小值时对应p值作为偏向参数。偏向参数的确定流程如下:

①设步长为λ,取p的初始值p0为相似度矩阵中值2倍,按式(9)迭代增加p值,即

pi+1=pi+λ,i=0,1,…,ξ

(9)

式中:ξ为p增加的最大次数。

②对各p值下的RBF神经网络进行训练测试,按式(10)分别计算每次测试的RBF神经网络误差,即

(10)

式中:z为测试样本个数。

③若序列{ei}在eκ处取最小值,则取偏向参数为

p=pκ

(11)

步长λ的大小会影响p值,若过大,可能会错过最优p值选取。因此,为取到合适的p值,则在反复试验基础上,选取步长λ=0.001。偏向参数的寻优流程框图如图2所示。

由于以RBF神经网络测试误差为评价指标,按一定步长,迭代增加p值确定偏向参数,故使得RBF神经网络能取到合适的隐含层节点数,从而达到较高精度。

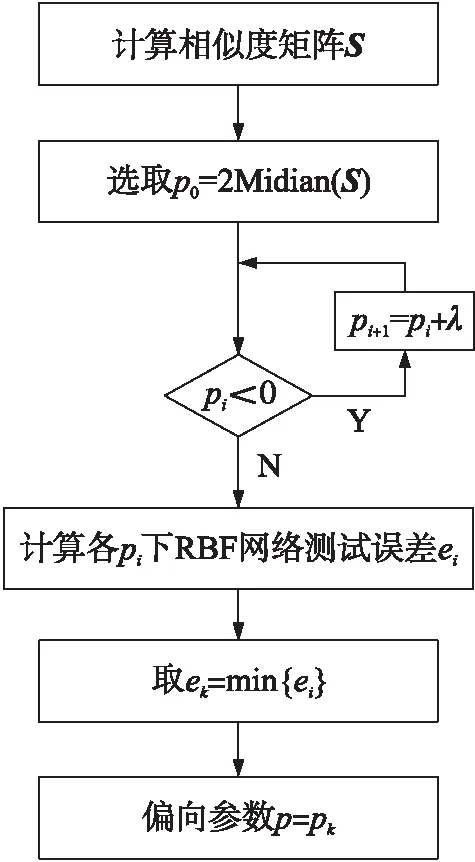
图2 偏向参数的寻优流程图

2.2 连接权值的自适应

用AP算法对训练样本聚类后,将测试样本归至某一类训练样本集。由于在该类集中必存在两个与测试样本至类代表点间距离相差最小的训练样本,则由高斯基函数特性可知,这两个训练样本与测试样本的隐含层输出值相差会较小,且它们在该类隐节点处输出值要远大于其他隐节点处输出值,因此可将其他隐节点处输出值全部置0。根据这两个训练样本在该类隐节点处实际连接权值,利用插值法计算测试样本在该类隐节点处连接权值,进而实现连接权值随测试样本的自适应调整。

算法具体运行过程如下:

①用AP算法对训练样本聚类,由聚类结果确定RBF神经网络相关参数,构建并训练RBF神经网络。

(12)

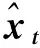
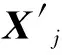
(13)

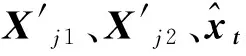
(14)

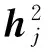
(15)

(16)

即

(17)

(18)

图3 连接权值自适应调整算法流程图

连接权值自适应调整算法流程框图如图3所示。通过对测试样本利用归类插值法,使连接权值随测试样本改变而自适应调整,避免有些测试样本因连接权值固定而产生较大输出误差,因此RBF神经网络精度将得到进一步提高。

3 试验与分析

3.1 获取试验数据

在跨海大桥公路连接线的试验场地上,均匀布置两条压电薄膜传感检测系统,对车辆动态情况下的称重系统进行工程实测试验。

试验车辆:选取三轴货车、四轴货车和六轴罐车等3种车型,共5种不同载荷。

试验条件:温度范围为16 ℃～29 ℃,车速范围为10 km/h～50 km/h。

试验前,分别对各试验车辆进行标定以获得它们的实际车重。试验共采集数据187组,具体数据如表1所示。

表1 试验基础数据

3.2 构建神经网络试验模型

一辆重为32.02 t的四轴货车驶过一条压电薄膜传感器,其产生的压电信号波形如图4所示。

图4 32.02 t四轴货车压电信号波形

受许多干扰因素的影响,压电信号中会含有大量噪声。以往学者在对压电信号进行降噪处理后,大都再通过经验公式[2-4]

G=KAV

(19)

计算车重。其中,G为车重值、A为压电信号各波形面积之和、V为车速、K为标定常数。由于此公式并未对温度、车速、车型等进行相应补偿,故导致车辆动态称重精度不高。因此,为提高车辆动态称重精度,且避开复杂的数学建模,则利用RBF神经网络构建车辆动态称重模型。

设两条压电薄膜传感器的压电信号各波形面积之和分别为A1和A2、传感器所处环境温度为T、车轴数为n。由式(19)可知,车重值G与AV成比例关系,则可将AV直接作为RBF神经网络输入向量的一个元素。为对两条压电薄膜传感器测量结果进行融合,且考虑温度、车型影响,则取A1V、A2V、T、n作为输入向量。由于最终测量结果为车重值,故仅取G作为输出向量。根据输入、输出向量,构建车辆动态称重RBF神经网络模型,如图5所示。

图5 车辆动态称重RBF神经网络模型

3.3 结果及分析

对187组试验数据,分别从各车辆试验数据中随机选取85%作为训练样本,剩余15%作为测试样本,构建基于AP聚类RBF神经网络车辆动态称重模型,并对其进行训练测试。其中,运算环境:CPU主频为2.30 GHz,2 Gbyte内存,Windows 7 32位操作系统,软件为MATLAB R2012a。

首先取p为相似度矩阵中值,得p=-0.386 5,则原算法的测试结果如图6所示。其次取p的初始值p0=-0.773,按步长λ=0.001,迭代增加p值,使得RBF神经网络测试误差为最小值时的p=-0.015,则偏向参数寻优算法的测试结果如图7所示。

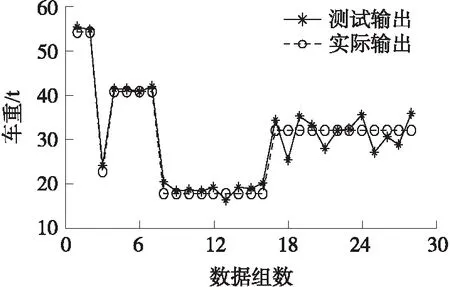
图6 原算法的测试结果

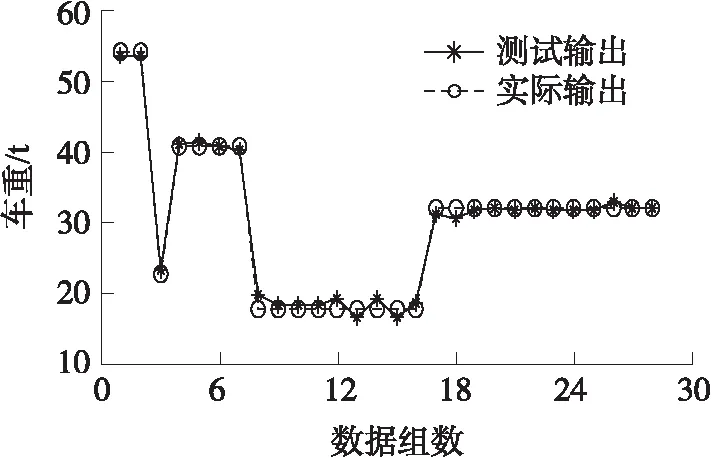
图7 偏向参数寻优算法的测试结果

由图6、图7可看出,当p=-0.386 5时,32.02 t四轴货车的测试输出与实际输出之间存在较大差异,而当p=-0.015时,差异度得到有效抑制,说明通过对偏向参数的寻优,提高了RBF神经网络精度。表2分别列出了当p=-0.386 5和p=-0.015时,32.02 t四轴货车的测试结果(称重误差均取绝对值)。表中可见,当p=-0.386 5时,最大称重误差为21.533 2%,而当p=-0.015时,最大称重误差为5.346 3%,较原算法减小4.03倍。

表2 32.02 t四轴货车测试结果

利用连接权值自适应算法对原算法进行改进,其中偏向参数仍取相似度矩阵中值,测试结果如图8所示。由图8可见,测试输出与实际输出几乎完全重合,说明连接权值经自适应调整后,RBF神经网络精度得到显著提高。

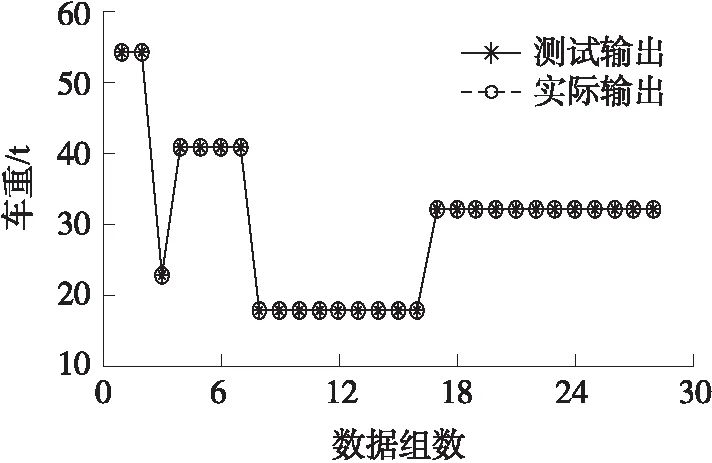
图8 连接权值自适应调整测试结果

表3列出了此时32.02 t四轴货车的测试结果,最大称重误差仅为0.269 6%,较原算法减小79.87倍。

连接权值经自适应调整后,若再对偏向参数进行寻优,得p=-0.46,测试结果如图9所示。

由图9可见,图9与图8几乎完全相同,且此时32.02 t四轴货车的最大称重误差为0.057 1%,说明RBF神经网络经连接权值自适应调整后,精度已达到很高,而偏向参数的寻优又使精度得到进一步提高。

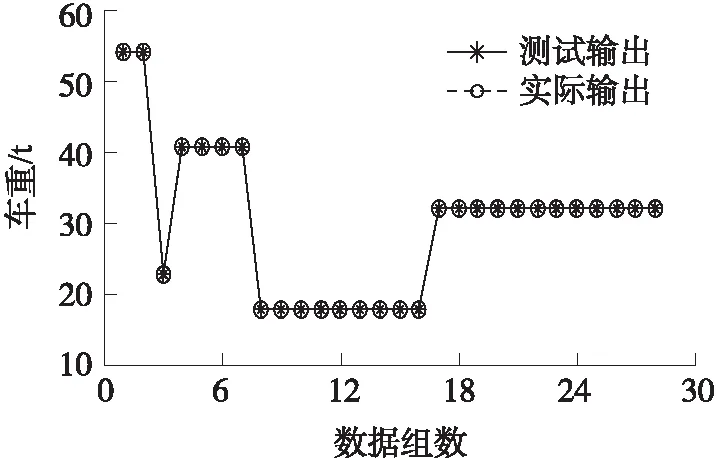
图9 连接权值自适应调整且偏向参数寻优的测试结果

为综合比较上述4种情况下RBF神经网络的精度、结构复杂度、训练速度、测试速度,则分别将它们的称重误差均值、隐含层节点数、训练时间、测试时间列于表4。

表3 32.02 t四轴货车测试结果(连接权值自适应调整)

表4 4种情况下的RBF神经网络测试结果

由表4可见,在对原算法改进中,连接权值自适应对RBF神经网络精度提高贡献最大,较原算法提高88.63倍,且网络结构也较简单,训练时间与原算法相同,但因需对测试样本归类插值求取连接权值,故测试时间较原算法增加0.026 9 s;若对原算法只进行偏向参数寻优,虽然RBF神经网络精度提高2.36倍,但隐含层节点数却为原算法3倍,导致网络结构变得复杂、测试时间较原算法增加0.000 1 s。同时,因进行偏向参数寻优逐次迭代,而致使训练时间增加;若对原算法进行连接权值自适应调整后,再作偏向参数寻优,则RBF神经网络精度达到最高,结构最简单,测试时间仍比连接权值自适应算法减小0.000 2 s。

由于神经网络训练完成后,是以一个固定函数模型进行输入、输出映射,故训练时间长短对网络输出实时性并无影响。本试验中,两条压电薄膜传感器间距为2.4 m,车速检测范围为10 km/h～200 km/h。因此,为验证网络在该试验中实时性,则提出如下实时性指标

τ=t1/t2

(20)

式中:t1为单个测试样本的测试时间、t2为车辆通过两条传感器的时间。为满足实时性要求,τ应小于1。

由于表4中的测试时间为28个测试样本总共所用时间,故单个测试样本的测试时间应为原来1/28倍。根据最高检测车速和表4中最大测试时间,计算得到t1max=0.000 975 s、t2min=0.043 2 s,则最大实时性指标值为

(21)

因此,RBF神经网络在改进前后均能很好满足实时性要求。

利用偏向参数寻优和连接权值自适应算法,按上述样本随机选取方法,对187组试验数据进行500次循环测试,并计算每次循环测试的称重误差均值,结果如图10所示。

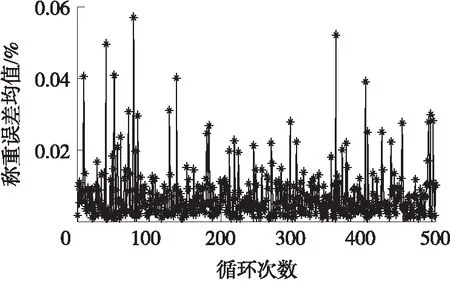
图10 AP聚类RBF神经网络改进算法循环测试

由图10可见,大多称重误差均值均在0.06%以内,其中有82.6%的称重误差均值低于0.01%。在500次循环测试中,RBF神经网络隐含层节点数为8个～10个、单个测试样本网络测试时间均值为0.000 964 s,对应最大实时性指标值为0.022 3。由此可知,基于AP聚类RBF神经网络改进算法具有很高的精度及实时性,网络结构简单、可靠。

4 结论

根据基于AP聚类RBF神经网络算法研究和试验结果分析,得到以下结论:

①按一定步长,迭代增加偏向参数,以RBF神经网络测试误差为评价指标,最终确定偏向参数,使RBF神经网络取到较合适的隐含层节点数,精度较原算法提高2倍以上。

②对测试样本利用归类插值法,使RBF神经网络连接权值随测试样本改变而自适应调整,精度较原算法提高80倍以上。

③将基于AP聚类的RBF神经网络改进算法应用于车辆动态称重系统,称重误差均值均控制在0.06%以内,最大实时性均值为0.022 3,且网络结构简单、可靠。该方法能有效满足车辆快速振动检测要求,对海洋工程结构振动信号检测和数据融合计算也具有重要的应用价值。

[1] 马宾,隋青美. 基于光纤微弯传感器的汽车动态称重系统设计[J]. 传感技术学报,2010,23(8):1195-1200.

[2] 李红杰. 汽车动态称重信号采集与处理方法的研究[D]. 武汉:中国地质大学,2012.

[3] 孙秀雅. 基于压电薄膜轴传感器的动态称重系统的研发[D]. 合肥:合肥工业大学,2014.

[4] 黄必飞,冯志敏,张刚,等. 压电薄膜车辆动态称重系统算法研究[J]. 传感技术学报,2016,29(6):941-946.

[5] 管硕,高军伟,张彬,等. 基于K-均值聚类算法RBF神经网络交通流预测[J]. 青岛大学学报(工程技术版),2014,29(2):20-23.

[6] 张永志,董俊慧. 基于模糊C均值聚类的模糊RBF神经网络预测焊接接头力学性能建模[J]. 机械工程学报,2014,50(12):58-64.

[7] 孙艳梅,都文和,冯昌浩,等. 基于蚁群聚类算法的RBF神经网络在压力传感器中的应用[J]. 传感技术学报,2013,26(6):806-809.

[8] Frey B J,Dueck D. Clustering by Passing Messages between Data Points[J]. Science,2007,315(5814):972-976.

[9] 王丽敏,姬强,韩旭明,等. 基于奇异值分解的自适应近邻传播聚类算法[J]. 吉林大学学报(理学版),2014,52(4):753-757.

[10] 谢文斌,童楠,王忠秋,等. 基于粒子群的近邻传播算法[J]. 计算机系统应用,2014,23(3):103-107.

[11] 孙劲光,赵欣. 一种改进近邻传播聚类的图像分割算法[J]. 计算机工程与应用,2017,53(6):178-182.

[12] 魏娟,杨恢先,谢海霞. 基于免疫RBF神经网络的逆运动学求解[J]. 计算机工程,2010,36(22):192-194.

[13] 石为人,陶芬,张元涛. 基于RBF神经网络的减摇鳍自适应滑模控制[J]. 控制工程,2012,19(6):978-981.

[14] 王慧,宋宇宁. 基于混合优化算法的压力传感器温度补偿[J]. 传感技术学报,2016,29(12):1864-1868.

[15] 张辉宜,周奇龙,袁志祥,等. 基于AP聚类的RBF神经网络研究及其在转炉炼钢中的应用[J]. 钢铁研究学报,2014,26(1):22-26.

[16] 张小俊,张明路,李小慧. 基于RBF神经网络的电化学CO气体传感器的温度补偿[J]. 传感技术学报,2009,22(1):11-14.

[17] 张辉,柴毅. 一种改进的RBF神经网络参数优化方法[J]. 计算机工程与应用,2012,48(20):146-149.