基于激励-校准法的硅微陀螺仪模态匹配控制电路研究*

吴 磊,杨 波*,王 刚

(1.东南大学仪器科学与工程学院,南京 210096;2.东南大学微惯性仪表与先进导航技术教育部重点实验室,南京 210096;3.惯性技术航空科技重点实验室,中航工业自控所,西安 710065)

硅微陀螺仪在近二十多年的研究历程中已经取得了长足的进步,目前已基本能满足中低端的导航制导和控制等军事、工业和消费类应用需求[1-2]。随着硅微陀螺仪研究的推进和深入,如何进一步提高硅微陀螺仪的精度,挖掘硅微陀螺仪的潜在能力,甚至突破其极限精度,是近年来硅微陀螺仪研究的热点问题。近年来,通过模态匹配技术来提高硅微陀螺仪精度受到广泛关注,成为一种最具有潜力研究途径之一。模态匹配技术主要是指通过一定的控制技术或者工艺手段实现硅微陀螺仪的检测模态和驱动模态匹配,根据硅微陀螺仪的工作原理,当检测模态与驱动模态匹配时,硅微陀螺仪可以实现最大的机械灵敏度[3-5]。受限于加工工艺,硅微陀螺仪的检测模态和驱动模态实际谐振频率很难保证与设计值相等,因此,频率调谐的后处理技术成为了研究重点。采用额外辅助工艺沉积或刻蚀多晶硅技术可以用来改变模态频率,但是这种方法需要人工介入,同时,由于这种加工方法是一次性的,受环境影响较大,很难实现完全且稳定的模态匹配[6]。随着研究的推进,后续出现多种借助控制技术的自动模态匹配方法。如文献[7]中提出的极值搜寻法,通过施加不同的敏感模态频率调谐电压步长,来监测敏感模态通道内零输入共模电压的峰值,根据峰值电压变化趋势寻找最大点,实现完全模态匹配,但这种方法是在开环条件下实现的,开环检测条件下系统稳定性较差,且该模态匹配方式只能单次运行,难以适应由周围环境温度、振动等导致的模态频率漂移等变化[8]。文献[9]提出了一种相域模态匹配方法,该方法利用驱动信号激励检测模态来获得调谐电压,但是该方法将显著增加哥氏信号的检测难度。

本文设计了一种基于激励-校准法的硅微陀螺仪实时模态匹配控制电路,利用双边激励信号激励检测模态,比较双边激励信号的幅值响应,然后利用静电负刚度效应软化弹簧刚度,降低检测模态的谐振频率,从而达到检测模态和驱动模态的频率匹配[10-11]。

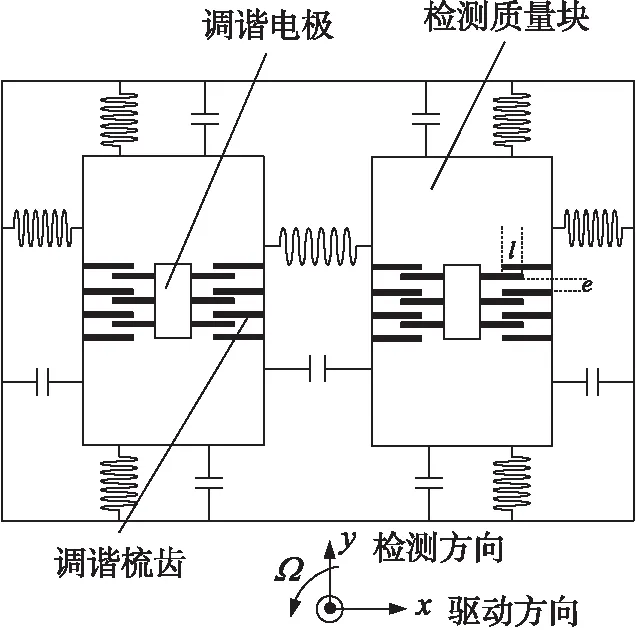
图1 集成频率调谐电极的硅微陀螺仪结构示意图

1 负刚度频率调谐原理

集成频率调谐电极的双质量块硅微陀螺仪结构原理示意图如图1所示,闭环驱动控制电路驱动质量块沿着x轴方向做简谐运动,在有z轴角速度输入时,根据哥氏效应,质量块将在y轴方向做简谐运动。该陀螺仪通过在检测质量块上集成调谐电极和调谐梳齿实现对检测模态的频率调节功能。在陀螺仪设计之初,其检测模态谐振频率被设置为高于驱动模态的谐振频率,在调谐电极上施加直流电压,利用调谐压膜梳齿的静电负刚度效应来降低检测模态的谐振频率,进而实现模态匹配。当直流调谐电压Vt加载在调谐电极上,其产生的静电负刚度为[12-13]:

(1)

式中:N为调谐梳齿个数,ε为真空介电常数,h为梳齿厚度,l为梳齿间重合的长度,e为梳齿间距,y为梳齿微小位移。因此,检测模态的谐振频率可以表示为:

(2)

式中:ks0为检测模态的初始静电刚度,ms为检测质量块的质量。式(2)可被进一步简化为

(3)

式中:b为检测梳齿中的机械常参数。

图2所示为测得陀螺仪的检测及驱动模态谐振频率与加载调谐电压大小的关系示意图。实验中,对陀螺仪的频率调谐功能做了开环测试,通过在调谐电极上施加不同的调谐电压,同时用频谱仪分别对驱动和检测模态做扫频测试,从而获得驱动和检测模态谐振频率与调谐电压的关系。从图2可看出,当施加的调谐电压达到6.658 V时,陀螺仪实现模态匹配。

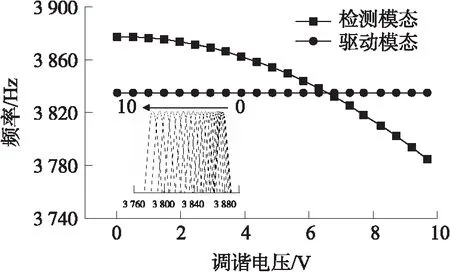
图2 检测及驱动模态谐振频率与加载调谐电压的关系

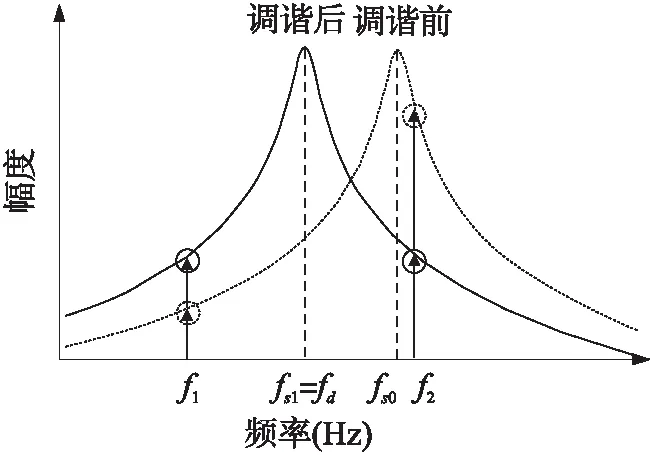
图3 基于激励-校准法的模态匹配机理示意图

2 基于激励-校准法的模态匹配控制电路方案

图3所示为基于激励-校准法的模态匹配机理示意图。通过在检测反馈电极上施加两路特定频率的激励信号,比较两路信号通过检测模态后的幅值响应差值来获得调谐电压。调谐前,两路信号通过检测模态后的幅值响应表现为有差值,在模态匹配后,两路信号的幅值响应近似相等。两路校准信号的频率关系满足

f2-fd=fd-f1

(4)

式中:fd代表驱动模态的谐振频率。

激励-校准法利用了检测模态的幅值响应关于其谐振频率的对称特性来获得调谐电压,但是这种对称不是完全意义上的对称,在幅值响应上存在着细微的差别。检测模态的传递函数可以表示为

(5)

式中:ws为检测模态的谐振频率,Q为检测模态的品质因数。双边激励信号的幅值响应可以表示为

(6)

在模态匹配完成时,A1=A2,根据表1的参数计算得到理论调谐频率结果为ws=3836.3×2πrad/s,与驱动模态谐振频率的差值为1.3 Hz,调谐误差为0.034%,实际控制方案中可以通过设置合适的PI控制器参考点来消除该项误差。

表1 调谐参数表

基于激励-校准法的模态匹配控制电路框图如图4所示。G(s)代表检测模态的传递函数,Kf-e为前端放大器,在FPGA内部通过直接数字式频率合成器(DDS)生成激励及解调所需要的两组不同频率的激励信号。

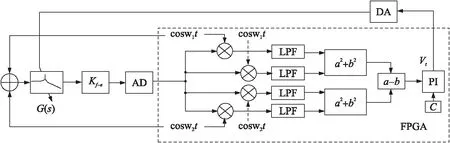
图4 模态匹配控制框图

AD采样后的信号可以表示为

Kf-e{A1cos(w1t+φ1)+A2cos(w2t+φ2)}

(7)

采样后的信号经过四路解调滤波后得到

(8)

经过平方相加运算后得到两路激励信号的幅值响应,因此,PI控制器的输入信号可以表示为

(9)

PI控制器的参考点设置为C,PI控制器的输出经过DA转换器得到对应的调谐电压并施加在调谐电极上,系统实现闭环模态匹配。

3 仿真与实验结果

为了进一步验证基于激励-校准法的模态匹配控制电路的可行性,在Simulink环境下搭建了基于图4的仿真控制模型,模型具体参数如表2所示。

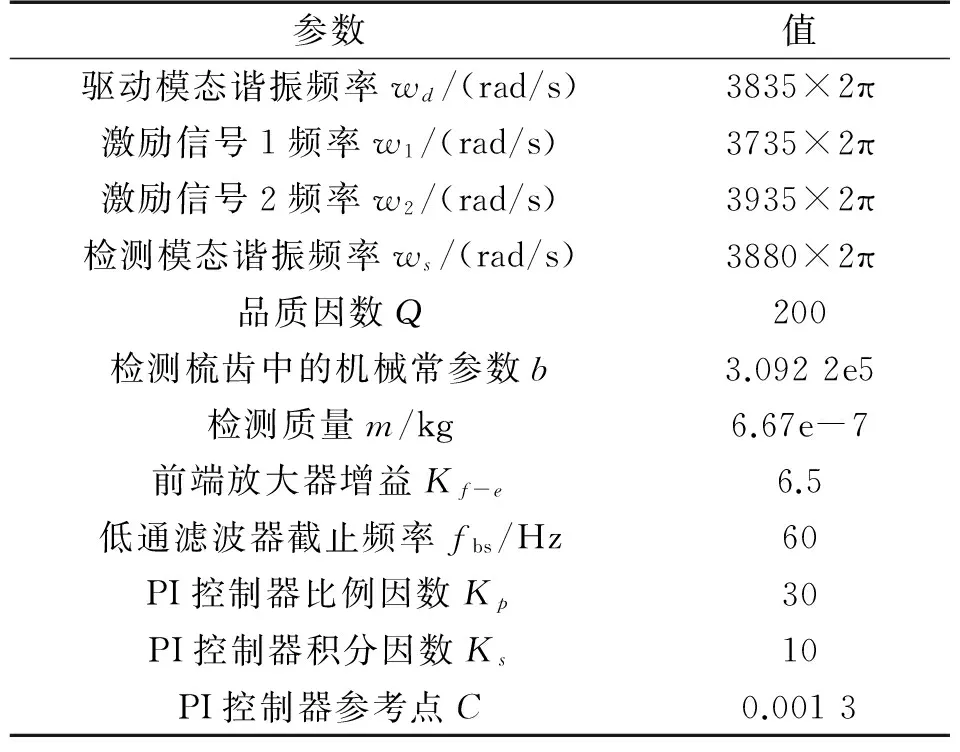
表2 模态匹配控制系统仿真参数

结合表2参数及式(3)计算得到调谐电压理论值为6.658 V,图5所示为仿真系统在调谐过程中得到的前置放大器输出曲线,PI控制器输入、输出曲线。从图中可以看出,前置放大器的输出为双边信号的调制波形,系统在启动后经过0.3 s左右的时间完成模态匹配,调谐电压稳定在6.658 V。

图5 调谐系统仿真结果

根据上述理论分析及仿真验证,设计了基于FPGA的模态匹配控制电路,如图6所示。

图6 陀螺测控电路

图7所示为实测模态匹配控制电路中前端放大器的输出频谱图,在静态条件下,耦合到检测模态的驱动信号幅值为-46 dB,双边激励信号幅值为-18.56 dB。

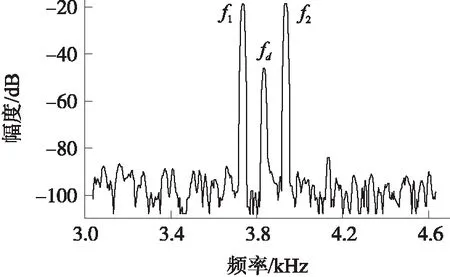
图7 前端放大器输出频谱图

图8所示为实测模态匹配控制电路调谐电压变化曲线,从图8可以看出,所设计的模态匹配控制电路仅需要0.5 s的时间即可完成模态匹配。调谐电压大小为6.68 V,对应的调谐频率为3834.69×2π rad/s,调谐差值为0.31 Hz,调谐误差为0.008%。

图8 调谐相应时间

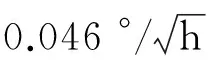
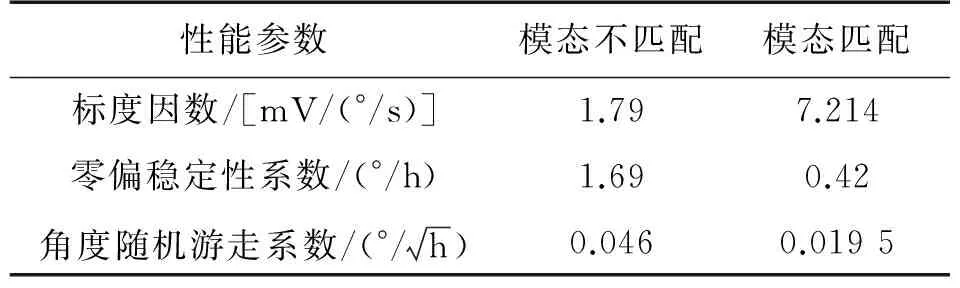
表3 陀螺仪性能测试结果

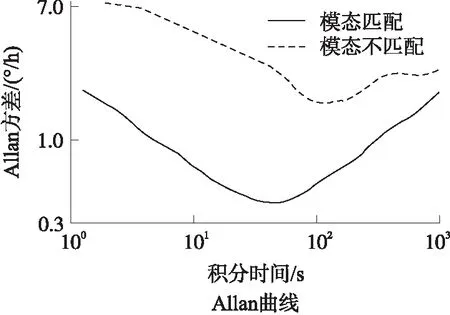
图9 被测陀螺仪在模态匹配及不匹配情况下的阿伦方差曲线图

4 结论

研究了一种基于激励-校准法的硅微陀螺仪模态匹配控制电路,首先介绍了基于负刚度效应的频率调谐原理,利用检测模态幅度响应关于其谐振频率对称的特点引入了激励-校准法,然后搭建了基于Simulink的仿真控制模型,仿真结果验证了该方案的可行性,最后设计了基于FPGA的自动模态匹配控制电路。实验结果表明,相比于模态不匹配条件下,模态匹配条件下的被测硅微陀螺仪的零偏稳定性系数和角度随机游走系数静态性能分别提升了4.02倍和2.36倍。

[1] 刘梅,周百令,夏敦柱. 对称解耦硅微陀螺仪结构设计研究[J]. 传感技术学报,2008,21(3):435-438.

[2] 王攀,黄丽斌,李宏生,等. 硅微陀螺仪闭环正交校正研究[J]. 传感技术学报,2013,26(3):357-360.

[3] Xu L,Li H,Yang C,et al. Comparison of Three Automatic Mode-Matching Methods for Silicon Micro-Gyroscopes Based on Phase Characteristic[J]. IEEE Sensors Journal,2016,16(3):610-619.

[4] 张印强,杨波,李婧,等. 硅微阵列陀螺仪的仿真、设计与测试[J]. 传感技术学报,2012,25(1):29-32.

[5] 杨成,李宏生,徐露,等. 基于低频调制激励的硅微陀螺仪自动模态匹配技术[J]. 中国惯性技术学报,2016,24(4):542-547.

[6] 陆学斌,刘晓为,陈伟平,等. 振动式微机械陀螺的带宽特性分析[J]. 传感技术学报,2008,21(2):337-340.

[8] Yesil F,Alper S E,Akin T. An Automatic Mode Matching System for a HighQ-Factor MEMS Gyroscope Using a Decoupled Perturbation Signal[C]//Transducers —2015,International Conference on Solid-State Sensors,Actuators and Microsystems. IEEE,2015:1148-1151.

[9] Sung W T,Lee J Y,Lee J G,et al. Design and Fabrication of Anautomatic Mode Controlled Vibratory Gyroscope[C]//IEEE International Conference on MICRO Electro Mechanical Systems. IEEE,2006:674-677.

[10] 杨波,吴磊,周浩,等. 双质量解耦硅微陀螺仪的非理想解耦特性研究和性能测试[J]. 中国惯性技术学报,2015,23(6):794-799.

[11] 邓允朋. 基于音叉效应的双质量块硅微陀螺仪结构优化设计[D]. 南京:东南大学,2016.

[12] 王存超,王寿荣,周百令. 基于随机平均法的MEMS陀螺自适应控制设计[J]. 仪器仪表学报,2008,29(4):841-844.

[13] 王行军. 硅微陀螺仪信号反馈及误差校正电路研究[D]. 南京:东南大学,2016.