基于JC法的输电塔轴心拉压构件可靠度分析

刘　堃，白　强，冯　衡，曾二贤

（中南电力设计院有限公司，湖北　武汉　430013）

0　引言

输电塔是输电线路中维系安全稳定运行的重要载体，随着我国电力行业的迅速发展，电网传输需求和容量不断扩大，电网系统的安全性和可靠性要求越来越高。特高压输电铁塔由于高度大，结构整体高宽比大，属于柔性结构，风荷载是输电塔结构体系的主要影响荷载。输电塔体系在自重恒载及风荷载作用下的安全性是首要关注的问题，运用简单有效的方法对其可靠度分析以及对应的失效模式判断将直接影响杆塔结构和输电线路的安全。

基于等效静风荷载模型，对输电塔荷载和构件抗力进行统计分析，根据抗力功能函数计算抗力效应标准值。通过随机过程的统计参数信息对输电塔构件进行可靠度分析。通过典型轴心构件的可靠度分析，总结了可靠度与荷载效应关系，可有效指导输电塔构件设计。

1　JC法原理

JC法的主要思路是将非高斯随机过程进行高斯过程的转化，然后通过一次二阶矩求解可靠度。

2）由式（1）～（4）求等效高斯过程的 μ′Xi，σ′Xi，用μ′Xi，σ′Xi代替 μXi，σXi。

当非高斯过程Xi为对数高斯分布时，其等效高斯随机过程的均值、均方差可由式（1）、（2）计算。

当非高斯过程Xi服从极值Ⅰ型分布时，其等效高斯过程的均值、均方差可由式（3）、（4）计算。

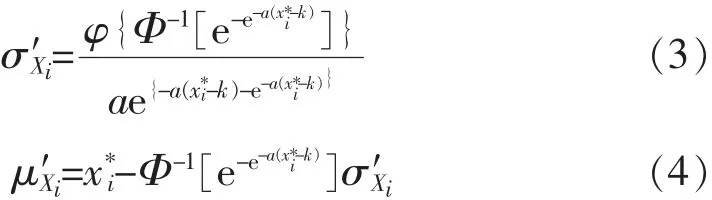
3）计算 cosθXi

式中：P*为设计验算点；Z=g（X1，…，Xn）为功能函数。

4）计算可靠指标β

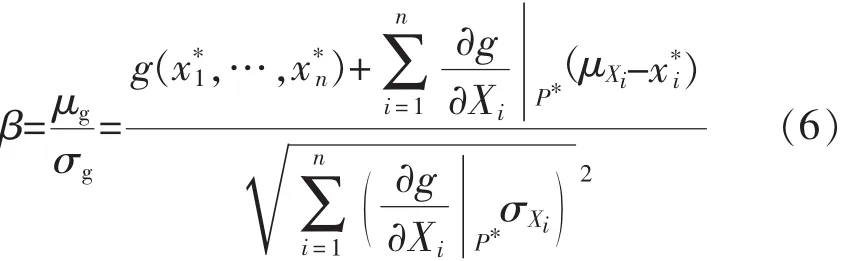
5）计算新的验算点坐标

6）选取新的验算目标，重复 2）～5），至误差值小于预设误差值计算收敛。

2　杆塔构件可靠度分析的参数分析

2.1　荷载的统计分析

2.1.1　永久荷载分析

输电线路中，对于输电塔的内力分析一般采用一阶弹性方法，一般认为荷载效应的统计特性与荷载值保持一致。输电塔结构永久荷载包含塔身自重、电线、绝缘子、金具自重以及固定设备自重。工民建构筑物的可靠度计算中永久荷载可基于建筑统计数据得，而输电塔结构尚缺乏相关统计信息，因此做如下处理。

杆塔构件自重

结构构件的几何参数不定性主要指制作尺寸偏差和安装误差引起的构件几何参数变异性，根据对结构构件抗力的影响程度，一般构件可仅考虑截面几何参数变异性。其中，γ和l分别为钢材重度和构件长度，其变异性可忽略，截面特性A的均值系数和变异系数分别为KA=1.00，VA=0.05。因此杆塔自重荷载统计参数主要由截面特性控制，由此取KG=KA=1.00，VG=VA=0.05。

2.1.2　风荷载统计分析

输电塔结构中可变荷载包括风荷载、电线绝缘子的覆冰荷载以及临时施工荷载等，风荷载是其主要的控制荷载。风压值、风攻角、体形系数和风压高度变化系数均可影响风的变异性[1-2]，其在设计基准期为50年时的计算表达式为

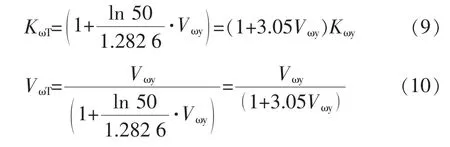
式中：Kωy为风荷载均值系数，其值等于均值与标准差的比值；Vωy为风荷载变异系数，其值等于标准差与均值的比值；KωT和VωT分别为50年周期内的均值系数和变异系数。

以糯扎渡±800 kV输电线路的云南省广南县为例，T1表示周期，KωT和 VωT的计算结果分别如表1、表2所示。

表1　均值系数计算表

表2　变异系数计算表

2.2　构件抗力的统计分析

根据DL／T 5154—2012《架空送电线路杆塔结构设计技术规定》，轴心受力构件的设计表达式为

式中：N为轴心拉力或轴心压力设计值；φ为稳定系数；m为构件强度折减系数；mN为压杆稳定强度折减系数；An为构件净截面面积；f为钢材的强度设计值，对多排螺栓连接的受拉构件，要考虑锯齿形破坏情况。

影响结构构件抗力的因素很多，在分析结构构件可靠度时常考虑的主要因素包括材料性能的不确定性，几何参数的不确定性，计算模式的不确定性，构件抗力R可以表达为

式中：Kp、KA、Kσ分别为计算模式、截面几何特性以及材料强度不确定性；Rk为构件抗力标准值[1]。

考虑上述不确定性后构件抗力均值系数与变异系数为

参考《钢结构可靠度分析》计算结果如表3所示。

表3　不同种类轴拉钢材可靠度统计参数

抗拉抗力的统计参数为：KR=1.092，VR=0.108。轴心受压构件计算结果如表4所示。

表4　不同种类轴压钢材可靠度统计参数

忽略初弯曲、残余应力和柱长的变异影响，临界应力不确定性仅受材料长细比λ、材性M，弹性模量E 的变异性影响[3]。

对于输电塔结构这种主要以螺栓连接构件组成的体系，用B类柱受压分析其可靠指标[4-5]，不同长细比均值系数和变异系数表如5所示。

表5　不同长细比均值系数和变异系数

2.3　构件可靠指标计算

2.3.1　设计表达式和功能函数

本研究中，主要考虑恒载和风荷载。规范设计表达式为

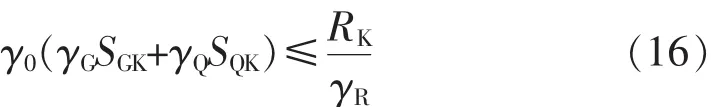
式中：γ0为结构重要性系数；γG、γQ、γR分别为永久荷载、可变荷载和构件抗力分项系数；SGK、SQK分别为永久荷载效应标准值、可变荷载效应标准值[1]。对±800 kV直流线路采用一级，杆塔结构重要性系数取1.1～1.2。 依据规范取γG=1.2，γQ=1.4，Q345 钢γR=1.11。

2.3.2　可靠指标计算步骤

1）给定各荷载效应标准值SGK、SQK、SiK，由设计表达式计算抗力效应标准值RK；

2）由统计参数信息，各随机过程的均值和标准差为

3）采用JC法计算已知功能函数下的可靠指标[6]。

3　拉压构件可靠度计算

3.1　轴心受拉构件

随机变量统计参数如表6所示。

表6　随机变量统计参数

Q345钢材荷载效应比对轴心受拉构件可靠度影响规律如图1所示。

图1　荷载效应比ρ对Q345轴心受拉构件可靠指标β的影响

比较相对高度在0.2和0.5时，可靠指标随荷载效应比变化曲线可知：当荷载效应比在0～2之间时，可靠度指标取值在3.0以上，其衰减速率较快。当荷载效应比大于3时，可靠度指标变化较为平缓。T1为0.2 s、1.0 s、1.5 s时曲线基本重合，随着荷载效应比的增大，可靠指标不断减小，其衰落速率逐渐减小。当荷载效应比大于4时，衰落速率较低，可知此后可靠指标对荷载效应比的敏感性较低。相对高度为0.2时，ρ从0.25增大到2的过程，可靠指标衰减27%，衰减速率为15.4；从2增大到4的过程，可靠指标衰减5%，衰减速率为2.5；从4增大到8的过程，可靠指标衰减3.6%，衰减速率为0.9。相对高度为0.5时，可靠指标与荷载效应比的关系与相对高度为0.2时类似，说明可靠指标对相对高度不敏感。综上所述，轴心受拉构件可靠度与荷载效应比呈现典型负相关，与相对高度关系较小。2.0和4.0的荷载效应比，均是可靠度指标衰落的控制点。

3.2　轴心受压构件

荷载效应的统计参数与轴拉构件相同，统计Q345钢材长细比对轴心受压构件可靠度影响规律。

3.2.1　长细比λ影响分析

由图2可知，在不同条件下，可靠指标均与长细比呈现负相关，随着长细比增大，可靠指标衰减速率在长细比为60时呈现明显转折[7]。在荷载效应比为0.5时，长细比在20～60的过程，可靠指标衰减幅度均值为6.8%；长细比在60～120的过程，可靠指标衰减幅度均值为5%。在荷载效应比为2时，长细比在20～60的过程，可靠指标衰减幅度均值为4.2%；长细比在60～120的过程，可靠指标衰减幅度均值为3.4%。长细比为60是可靠指标衰减的控制点。

图3　荷载效应比ρ对Q345轴心受压构件可靠指标的影响

3.2.2　荷载效应比ρ影响分析

与轴心受拉构件相似，轴心受压构件可靠指标与荷载效应比呈现典型的负相关。在长细比为20时，ρ从0.25增大到2的过程，可靠指标衰减均值为35%；从2增大到4的过程，可靠指标衰减6%；从4增大到8的过程，可靠指标衰减3.4%。在长细比为60时，ρ从0.25增大到2的过程，可靠指标衰减均值为32%；从2增大到4的过程，可靠指标衰减6.8%；从4增大到8的过程，可靠指标衰减3.4%。

综上所述，轴心受压构件可靠度与荷载效应比和长细比呈现典型负相关，2.0和4.0的荷载效应比，长细比60，均是可靠度指标衰落的控制点。

4　结语

输电塔构件在自重荷载和风荷载作用下的可靠度计算对于整体结构的安全性至关重要。对于轴心拉压构件，在设计时需要考虑荷载效应比和长细比的影响。

对于轴心受拉构件，构件可靠度与荷载效应比呈现典型负相关，与相对高度关系较小。2.0和4.0的荷载效应比，均是可靠度指标衰落的控制点。

对于轴心受压构件，在不同条件下，可靠指标均与长细比呈现负相关。长细比为60，是可靠指标衰减的控制点。轴心受压构件可靠度与荷载效应比呈现典型负相关，2.0和4.0的荷载效应比均是可靠度指标衰落的控制点。

[1]中华人民共和国建设部.建筑结构可靠度设计统一标准：GB 50068—2001[S].北京：中国建筑工业出版社，2001.

[2]欧进萍，段宇博，叶骏.等效随机静风荷载的模型及其参数确定[J].哈尔滨建筑大学学报，1994，27（2）：1-8.

[3]李继华，夏正中，陈国兴.钢结构轴心受压构件可靠度分析[J].建筑结构学报，1985，6（1）：2-17.

[4]夏正中，朱文.钢压弯构件的可靠度分析[C]∥中国土木工程学会桥梁及结构工程学会学术会议.1987.

[5]戴国欣，李继华,夏正中．高层钢框架柱的概率评估[J]．重庆建筑工程学院学报，1992，14（2）：1-9.

[6]陈海波，廖宗高，肖洪伟.受风荷载控制的杆塔结构体系可靠度分析[J]．电力建设，2007，28（7）：40-42.

[7]李彦民．送电线路杆塔结构风荷载作用下可靠度分析及应用研究[D]．重庆：重庆大学，2007．