OFDMA中频谱感知的功率控制算法研究
李永芳,庄文学,张一晋
(1.南京铁道职业技术学院 通信信号学院,江苏 南京 210031;2.南京理工大学 光电学院,近程高速目标探测技术国防重点学科实验室,江苏 南京 210094)
0 引言
功率控制是认知无线电[1]的关键技术之一。在认知无线电系统中,发送功率与信干比紧密相关,认知用户在满足信干比的情况下,发送功率越小越好。增大发送功率可获得较好的信干比,同时对其他认知用户造成干扰。减小发送功率有可能使认知用户的信干比低于目标值。为解决发送功率与信干比之间的制约关系,必须对发送功率进行控制。
目前,认知无线电系统中基于博弈论的功率控制算法已有一些研究成果,其目的是寻求一个最佳的策略组合使每个参与者都是其他参与者策略的最优反应,其出发点都是减少发射功率,来增大公平性。文献[2]提出了一种非合作博弈功率控制模型,即根据认知用户的服务质量(QoS)需求来控制发射功率,使系统吞吐量最大。为了兼顾公平,文献[3-6]通过引入动态调整机制,提出了一种基于动态代价的功率控制博弈算法,从而改善系统性能。文献[7]提出了一种支持动态服务区分兼顾公平性的退避算法——服务区分动态退避(SDDB)算法。文献[8]根据不同链路增益的功率博弈控制算法,对不同路径增益的用户设计不同的惩罚函数。文献[9]研究了授权用户在保障其最低服务质量时,认知用户需要自适应调节发射功率使其干扰最小。此外,文献[10]提出了基于干扰温度的代价函数。文献[11]提出了一种基于频谱感知的功率自适应阈值分配算法,引入了局部干扰模型。以上算法在一定程度上考虑到了各用户间的公平性,但是没有考虑到干扰温度引起的局部干扰现象,忽略了认知用户最小信干比要求。
好的频谱共享方案能够通过为多个用户分配有效的带宽来获得高的系统容量。OFDMA[12]不仅可以通过跳频技术来克服多径频率选择性衰落,增加频率分集,很好地抵抗多径效应,还可以根据每个子载波上的衰落情况动态地调整每个子信道上所采用的调制解调方式、发射功率、编码方法、载波频率等实现多址接入,提高频谱利用率[12]。
本文受功率阈值算法[11]的启发,建立了PA-OFDMA仿真模型,根据频谱感知,自适应地为每个子信道分配功率阈值,同时通过限定使用该信道的认知用户最大发射功率,避免干扰温度的影响,具有较低的误比特率。
1 功率阈值算法
在2003年,FCC提出了干扰温度[14]的概念用来“量化和管理”干扰。通过该模型,认知无线电可以测量当前的干扰环境,调整它们的发射特性。因此,可以实现动态频谱共享而避免对授权用户产生有害的干扰。
为了解决局部干扰,可以采用基于频谱感知的功率自适应阈值分配算法,在该算法中需要满足:
PS(f)≤[BkTL(fc)-PI(f)]/α。
(1)
因此授权接收机总的干扰要低于干扰温度限。
PT(fc)≤max[αPS(f)+PI(f)]≤BkTL(fc)。
(2)
根据式(2)可以通过改变非授权用户的发射功率解决局部干扰问题。
在功率自适应阈值分配模型中,基带信号的s(t)可以通过下式表达:
(3)
式中,di为第i个子信道上数据符号,T表示每个符号的周期。
假设每一个子信道的带宽为ΔB,并且fini=fc-B/2,则第i个子信道的非授权信号的平均发射功率阈值可以定义为:
(4)
并且满足:
(5)
式中,Blic⊂B表示授权用户使用的频带,TL(fi)表示第i个子信道上的频率函数。为了实现功率自适应,TL根据授权信号的存在与否,选择最大值或最小值,这样可以增加非授权信号的数据速率而不产生干扰。
当子载波数足够大时,非授权信号的发射功率可以在满足式(4)的前提下,使用授权频谱。为了使信道容量和频谱效率最大化,同时使绝对干扰最小化,每一个子信道上的非授权信号的发射功率应该和功率阈值相等,即:
(6)
根据式(3) ,基带OFDM信号的复合表达式如下:
(7)
式中,β表示功率自适应模型中调制方案所使用的平均符号功率。
但是,干扰温度模型的主要缺点是它只能控制平均干扰而不是绝对干扰。这样的话,就会出现在某些频带上绝对干扰温度超过干扰温度限,而平均干扰温度低于该限制的情况。这种部分干扰现象会给授权用户的接收带来很大的影响。所以在功率阈值模型中,通过恰当的功率阈值可以实现动态频谱共享。并且,可以得到非授权信号的功率谱,这将通过PA-OFDMA系统模型来实现。
2 PA-OFDMA系统
无线衰落环境中的动态频谱多址接入系统如图1所示。在该模型中,共有K个用户,且第k个用户的数据速率是Rkbit/OFDM符号。每个用户被分配一个或一组子载波,每个子载波只能分配给一个用户。整个带宽B被分成N个子信道,假设每个子信道上的信号带宽小于信道的相关带宽,因此每个子信道可以看成是平坦衰落信道。根据信道估计和频谱感知,给不同的用户分配不同的子载波,且每个子载波具有独立的功率约束条件,这通常取决于功率阈值。

从该模型框图中可以看出,功率阈值分配起着至关重要的作用。下面将重点讨论怎样设置功率阈值,以取得最大频带利用率和信道容量,同时避免干扰温度模型中的局部干扰现象。

图1 PA-OFDMA多址接入系统
3 PA-OFDMA的功率阈值分配算法
3.1 算法应用条件
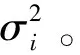
如果分配给第i个子信道的发射功率是P(bi),可以通过下式计算得到相应的负载比特数:
(8)
则该信道的最大传输速率是:
(9)
其中,Γ表示SNR间隔,可以根据调制方案多电平正交幅度调制(Multilevel Quadrature Amplitude Modulation,MQAM)所使用的“近似间隔”和系统误比特率BER计算得到:
(10)
因此功率分配可以概括为在约束条件Pbudget、PTH和BERmax下,使传输的比特数最大。即:
(11)
满足条件:
P(bi)≤PTH(i),∀i∈{1,2,···,N},
BERi≤BERmax,∀i∈{1,2,···,N},
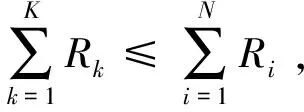
式中,PTH(i)是第i个子信道的功率阈值。可以通过Lagrange乘数法计算最优解:
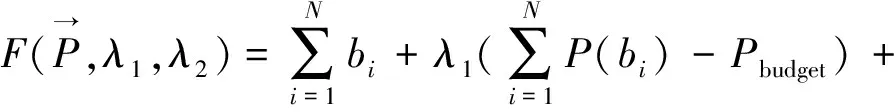
(12)
式中,λ1、λ2是Lagrange乘积因子。但是这种算法运算量大,算法复杂度高[16]。
3.2 算法
为了提高运算效率,假设阈值分配算法中对每一个子信道初始化时分配整数比特。首先,给所有的子信道分配相同的发射功率,即
Pini(bi)=min{Pbudget/N,PTH(i)}。
(13)
根据式(8)可以计算得到比特分配向量bini,并且每一个子信道的比特分配上限可以根据下式得到:
(14)
式中,γ表示PA-OFDMA系统中最大调制电平。可以通过四舍五入得到bi的整数:
(15)
式中,d表示调制方案中所使用的比特分配步长。初始化发射功率分配后,根据式(8)和式(15)可以计算得到功率向量P=[P(b1),P(b2),···,P(bN)]T。
为了减少总的发射功率,可以根据下面三步调整比特分配[17]:
① 当每一个子信道改变dbit的信息时,计算增加或减小的功率:
ΔP-(bi)=P(bi)-P(bi-d),
(16a)
ΔP+(bi)=P(bi+d)-P(bi)。
(16b)
② 删除功率减少最大的子信道,在剩下的子信道中找出功率增加最小的子信道。
(17)
③ 如果ΔP-(bn-)<ΔP+(bn+),则停止。如果第n+个子信道的功率阈值和总的发射功率均满足条件的话,则对发射功率进行调整:
P+(bn+)=P+(bn+)+ΔP+(bn+),
(18a)
P-(bn-)=P-(bn-)-ΔP-(bn-)。
(18b)
否则,从剩余的子信道中删除第n+个子信道,然后返回步骤①。
认知用户可以根据给每个子信道分配的功率阈值,控制它的最大发射功率,避免对授权用户产生有害的干扰。通过这个算法,在满足总的发射功率约束和每一路子载波功率约束的条件下,可以实现传输速率的最大化,即系统的吞吐量最大,同时整个系统的误比特率也较小。
4 算法仿真与性能分析
4.1 仿真条件
假设子载波数N=256,调制方案MQAM中M=2、4、16、64,信道是多径时延信道,具有150 ns的延迟扩展。系统抽样间隔是50 μs,循环嵌缀长度为32。为了更好地比较非授权信号的功率谱和多种频谱共享方法的性能,假设每一个OFDM符号周期为14.4 μs,子载波间隔为80 kHz。授权频带B=[0,20 MHz],授权信号存在于Blic=[5,15 MHz]。并且,假设信道估计和频谱感知是理想的,信道状态信息反馈延迟对于发射机来说可以忽略。
4.2 仿真结果与性能分析
如图2所示,一般的OFDMA功率谱波形和PA-OFDMA功率谱波形比较,可以看出PA-OFDMA发射功率谱较小,对授权系统的干扰小,能够更好地适应动态频谱环境,在该环境下非授权信号可以利用空闲频谱或者授权信号的频谱,实现频谱共享,提高频谱利用率。

图2 功率谱波形图
图3表示不同算法的两种频谱共享方案功率分配图。其中ITM表示干扰温度模型下的功率分配,PTM表示功率阈值模型下功率分配。从这两条功率曲线中可以看出在ITM模式下,在频率5~15 MHz上非授权信号的功率峰值超过了干扰温度限(40 dBm),而在PTM模式下,可以通过自适应的功率分配算法(Tmax,Tmin),限制非授权信号的发射功率,避免局部干扰现象,提高系统容量。

图3 ITM和PTM频谱共享下的功率分配图
图4和图5分别表示在非频谱共享(None)、ITM和PTM三种模式下的频谱利用率和误比特率曲线。从图中可以清楚地看出,由于功率限制的约束,尽管PTM方法的频谱利用率比ITM低,但是误比特率性能比ITM提高大约3 dB。从这两个图中可以看出使用PTM方法,可以取得较高的频谱利用率和较低的误比特率,同时对授权用户产生较小的干扰。

图4 频谱利用率 (BER=10-3)
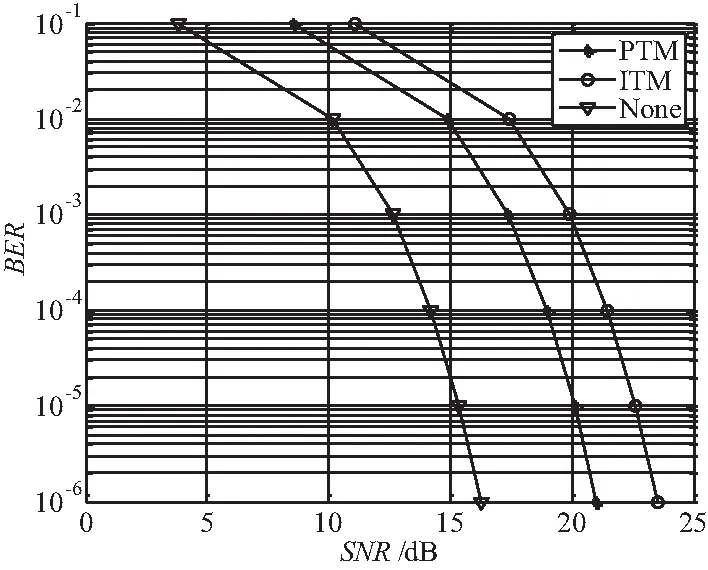
图5 BER和SNR曲线
5 结束语
本文针对功率控制算法中常忽略的干扰温度影响,结合功率阈值分配算法,建立一个认知环境下的多址接入(PA-OFDMA)仿真模型。通过限制认知用户的最大发射功率,自适应地为每个子载波设置发射功率,克服干扰温度模型中的局部干扰现象,实现频谱共享。仿真结果也表明该模型解决了干扰温度模型下的局部干扰现象,具有较高的频谱利用率和较低的误比特率,更符合认知无线环境中的实际分配现状,具有广泛的现实应用意义。
[1]Haykin S.Cognitive Radio:Brain-Empowered Wireless Communications[J].IEEE Journal on Selected Areas in Communications,2005,23(2):201-220.
[2]Lu Qianxi,Tao Peng.Utinity-based Resource Allocation in Uplink of OFDMA-based Cognitive Radio Networks [J].International Journal of Communication Systems,2010,23(2):252-274.
[3]胡图,景志宏,李冯敬.一种改进的认知无线网络功率控制博弈算法[J].计算机科学,2012,39(2):75-79.
[4]吴迎笑,杨震.OFDMA中频谱感知的功率控制算法[J].仪器仪表学报,2010,31(6):1235-1240.
[5]邱晶,邹卫霞.认知无线电中的动态频率选择和功率控制研究[J].系统仿真学报,2008,20(7) :1821-1826.
[6]程世伦,杨震.基于信干比的认知无线电自适应功率控制算法[J].电子与信息学报.2008,30(1):59-62.
[7]李瑞芳,李仁发.一种Ad Hoc网络信道接入退避算法及仿真分析[J].系统仿真学报,2007,19(1):141-144.
[8]Yu Hui,Gao Lin.Pricing forUplink Power Control in Cognitive Radio Networks [J].IEEE Transactions on Vehicular Technology,2010,59(4):769-778.
[9]Bu Shengrong,Yu Richard.Green Cognitive Mobile Networks with Small Cells for Multimedia Communications in the Smart Grid Environment [J].IEEE Transactions on Vehicular Technology,2014,63(5):2115-2126.
[10] Li Hongyan,Gai Yibing,He Zhiqiang.Optimal Power Control Game Algorithm for Cognitive Radio Networks with Multiple Interference Temperature Limits[C]∥ IEEE Vehicular Technology Conference,Vtc Spring 2008,Singapore.DBLP,2008:1554-1558.
[11] Wong C Y,Cheng R S,Lataief K B,et al.Multiuser OFDM with Adaptive Subcarrier,Bit,and Power Allocation [J].IEEE Journal on Selected Areas in Communications,1999,v17(10):1747-1758.
[12] Fazel K,Kaiser S.Multi-carrier and Spread Spectrum Systems[M].New York:John Wiley & Sons Ltd,2003.
[13] Wang Xi, Giannakis G B.Resource Allocation for Wireless Multiuser OFDM Networks [J].IEEE Transactions on Information Theory,2011,57(7): 4359 - 4372.
[14] Clancy T C,Arbaugh W A.Measuring Interference Temperature [C]∥Virginia Tech Symposium on Wireless Personal Communications,2006.
[15] Mohamed-Pour K,Shahraki H S.Efficient Power Loading in MIMO-OFDM Based Cognitive Radio Networks [J].Communications & Network,2011,3(1):8-16.
[16] Cioffi J M,Dudevoir G P,Eyuboglu M V,et al.MMSE Decision-Feedback Equalizers and Coding Part I: Equalization Results [J].IEEE Transactions on Communications,1995,43(10):2595-2604.
[17] Papandreou N,Antonakopoulos T.A New Computationally Efficient Discrete Bit-loading Algorithm for DMT Applications [J].IEEE Transactions on Communications,2005,53(5):785-789.

