极化特性在卫星通信系统中的应用研究
郭道省,张晓凯,张邦宁,齐 帅
(陆军工程大学 通信工程学院,江苏 南京 210007)
0 引言
卫星通信作为现代通信的重要方式,具有覆盖范围广、组网灵活、通信频带宽、通信容量大、可靠性高、便于多址连接等优点,所以在众多领域具有广泛的运用[1]。
根据电磁学理论,电磁波除了幅度、相位和频率特性之外,还具有极化这一基本特性。事实上,电磁波作为无线信号的传播载体,极化特性也是信号处理中可利用的重要资源。极化[2-3]是电磁波的电场矢量在传播截面上随时间变化的轨迹。充分利用电磁波的这一物理特性,能够打开卫星通信中一个新维度。通过对电磁波极化特性进一步分析、处理,可以丰富信号传输理论,提高传输可靠性,缓解当前卫星通信系统中频谱资源紧张、能耗高、干扰严重等问题[4],可为未来卫星通信系统容量提升、能耗降低、干扰消除等热点问题开辟新的途径[5]。
本文对信号极化特性在卫星通信传输中的应用现状进行分析,结合当前极化信息理论和最新研究成果,分析极化特性在卫星通信中的发展趋势。
1 国内外研究现状
极化信息处理在卫星通信中的应用起源于解决卫星天线与地球站天线对齐后匹配接收问题。卫星通过极化匹配来最大化接收有用信号,否则接收效果会很差[6]。地球在不断地做自转,微弱的卫星信号要被及时地捕捉,除了地球站对准卫星以外,还需要极化角的数值调整馈源输出波导口的方向,从而使得有用信号不泄露。例如目前仍在活跃研究的双频段、双频率圆极化天线[7-8]等。
随着卫星功能的不断扩展和数量的不断增加,电磁波的频率资源越发紧张,卫星的频段从4/6 GHz不断扩展到目前的太赫兹卫星,频率不断升高。虽然暂时解决卫星数量的矛盾,但频率越高,大气等对电磁波的吸收越严重,对器件的制造工艺要求越高,导致卫星的成本非常高。因此,利用类似于光纤通信中偏振复用技术的卫星极化复用技术孕育而生,其通过相互正交的极化信号实现对频谱的复用。采用双极化复用,当极化鉴别度(Cross-polarization Discrimination, XPD)达到20~39 dB就可以将频率资源利用率提升将近一倍[9]。正交极化复用技术关键在于极化复用实现的机理以及卫星信道的去极化效应等[10-11]。可见卫星正交极化复用可以在一定程度上解决频率资源紧张的问题。随着技术发展,正交极化复用已经无法满足日益增长的需求,有学者提出多极化复用,并为了克服去极化效应设计了最优的补偿策略[12]。
极化调制作为一种新的调制方式,其主要的优点是信号不受放大器的非线性影响、不受相位噪声的影响以及具有较高的频谱效率,在卫星通信领域的研究也不断展开[13]。因为,大多数卫星上都装配有双正交极化天线,因此无需硬件调整即可实现极化调制。同时,在极化调制解调时,无需严格的载波同步,适用于高动态以及高频窄带等难以建立载波同步的卫星通信系统等。
卫星通信系统由于其自身的广播特性以及较大范围的覆盖,所以面临着严重的传输安全威胁[14]。随着计算机能力的提升,传统高层加密技术无法完全保证信息的绝对安全传输。有学者设计一对快速跳变的双极化状态同时用于承载调制信息,形成一种自干扰[15],得以安全传输。
在卫星通信系统中,对这一信息资源研究开发的深度和广度还远远不能与其重要性相称。充分挖掘和利用潜在的极化域资源是未来卫星通信中重要的研究方向。
2 极化特性与卫星通信极化信道模型
电磁波完整的描述需要电场强度、电位移密度、磁场强度和磁通量密度四个基本场矢量。例如,在单一频率下已知电场强度,并采用其端点作为时间函数所形成的空间轨迹的形状和旋向定义电磁波极化状态,则其余场矢量可根据电场强度求出。一般情况下,简谐平面波电场强度的矢量端点在传播的横截面上随时间变化的轨迹是椭圆,称为极化椭圆。
2.1 当前电磁波极化信息的表示
对于完全极化波通常有5种常用的极化描述:电磁波的Jones电场矢量E、复极化比ρ、极化椭圆几何描述子(ε,τ)、极化相位描述子(δ,φ),以及Stokes矢量J。5种参数都可以唯一地表示一种极化状态。通常选定水平/垂直极化(H,V)作为一组基。在电磁波传播过程中,电场和磁场相互转换,所以用电场表示E=EhH+EvV,E=[Eh,Ev]T,则Jones矢量与极化相位描述子表示:
(1)
式中,γ称为极化角,取值范围为[0,π/2],δ称为极化辅角,取值范围为[-π,π]。George Stokes引入4个参数组成的Stokes矢量,更加形象地描述极化状态,如式(2)所示:
(2)
其中:g02=g12+g22+g32,φ=φV-φH,在功率密度一定时,选择g1、g2和g3作为一组三维的正交基。为了在球坐标下便于描述,采用方位角和仰角表示成为极化椭圆几何描述子(ε,τ)。Jones矢量、Stokes矢量和几何描述子,在归一化功率下,可以映射在Poincare极化球上,如图1所示。

图1 在Poincare上相位描述子与几何描述子
不同表示参数之间关系为:
(3)
式中,A为信号幅度,可做归一化处理。
2.2 极化与天线
电磁波由天线辐射,所以天线的极化特性即为该天线辐射电磁波所具有的极化特性。不同结构的天线具有不同的极化特性,若要对极化信息更加灵活运用,需要产生快速捷变极化信号。随着天线技术的发展,改变天线结构或者变更馈线内的电磁波模式就可以实现任意极化状态[16]。
改变天线结构的变极化装置最早在雷达极化场景下应用,有栅网极化变极化器[17]、反射型极化变极化器[18]、平行金属片极化变极化器[19]等。目前,变更馈线内电磁波模式的变极化天线应用较为广泛。在馈线内完成变极化,主要有半导体变极化器[20]和铁氧体变极化器[21],其分别依赖半导体相移、铁氧体移相器来实现变极化。半导体主要适用于S频段以下,铁氧体适用于S波段到Ku波段。这两种变极化器能够承受较大的峰值功率,可靠性高。矢量天线阵列[22](Vector Antenna Array,VAA)也是合成任意状态的极化波的一个新方法,其使用p(p>1整数)对点偶极子和磁偶极子通过功率控制即可产生。它的主要优点是能够较为精确地产生确定的极化信号,但是矢量天线阵列价格较为昂贵,一般装载于军用通信卫星和军用雷达中。
然而,基于硬件产生的极化信号的捷变速度较慢,容易受到机械损伤或者产生的复杂度较高,难以在以最新极化理论为背景的实际通信系统中广泛应用。
2.3 虚拟极化技术
虚拟极化技术 (Virtual Polarization, VP)与硬件变极化不同,其主要通过数字信号处理技术来产生任意的极化状态,它最早由英国学者Poelman[23]提出。VP技术利用一对双正交极化通道,对两个通道进行幅度和相位加权的数字信号处理,然后分别馈给极化正交天线或者一根双极化天线,即可在空间中形成任意极化状态的电磁波。由于目前数字信号处理算法的发展以及高性能极化捷变天线的出现,VP完全可以由DSP完成,整个通信系统无需额外的变极化器或改变天馈系统参数,大大提高了系统灵活性。
VP技术产生任意极化状态的原理,如图2所示。选取一组正交双极化天线辐射电磁波,通常选取水平(H)和垂直(V)极化天线,也可选取左旋圆极化和右旋圆极化等。

图2 虚拟极化发射机
其中,图中功分单元(Power Divide Unit, PDU)和相移单元(Phase Move Unit, PMU)分别为:
(4)
(5)
式中,(γT,δT)为辐射后的极化状态相位描述子。假设源信号是一个幅度为E0、频率为ω0的基带信号,经过PDU和PMU后,在双正交天线端口的信号为:
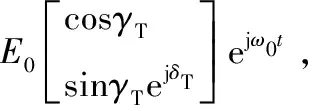
(6)
由此可见,可以调整相位描述子(γT,δT),使发射信号遍历所有极化状态,即产生任意状态的发射信号。
接收信号与发射是互易过程,如图3所示。

图3 虚拟极化接收机
在双正交天线接收信号后,通过两个通道的移相和幅值加权,即可等效获得任意状态的接收极化。接收端需要有发送端先验极化状态个数,通过遍历判决极化状态。设置幅度加权单元和相位加权单元分别为:
(7)
(8)

(9)
经过相干合成后,进入接收机的信号为:
yr=(RVcosγr+RHsinγrejδr)ejω0t,
(10)
则整个系统等效的接收极化状态即为相位描述子(γr,δr)。
在实际系统中,天线系统一般都满足互易定理。变极化天线将某线极化信号变成圆极化发射,同样也可以将该圆极化信号接收变成线极化而无损失。这意味着实现发射变极化天馈系统同样也可以接收变极化信号。对于虚拟极化而言,按照不同的复数权值加以组合,无损耗地快速产生任意极化状态,并使用接收机快速实现极化自适应,匹配相应的状态,达到最优化接收。因此,VP技术在未来极化信息的利用上将会发挥重要作用。
2.4 传统卫星信道特点
卫星信道与地面无线信道具有很大的区别,其主要特征有[24]:第一,功率受限,由于卫星主要依靠太阳能电池板工作,数字通信系统为其主要载荷,而星上功率放大器、体积以及散热都有很高的要求;第二,带宽受限,随着卫星数量的不断增加,原本有限的频谱资源变得异常紧张;第三,干扰和噪声影响大;第四,由于无线电波的无界性以及覆盖范围十分广阔,其依靠高层加密技术的安全传输面临严峻考验。
2.5 卫星信道的去极化效应
在卫星通信中,主要存在以下两种去极化机制[4]:
① 天线去极化:由于天线极化特性并非完全理想,天线既可以收到主极化的能量,也会接收到少许交叉极化状态上的能量。
② 基于反射的去极化:由于卫星信道穿过大气,会受到大气中的水蒸气、小冰晶等的反射与折射,以及对流层的闪烁,随机改变电磁波的极化状态,例如从水平极化状态变为垂直极化状态,出现功率耦合等现象。
由于信道的去极化效应,使得极化状态发生变化。从时域上看,主要存在无线极化信道之间的极化相关性和极化功率不平衡[25-26]。极化相关性体现为非富散射环境下极化信道之间的相关性;极化功率不平衡体现为实际信道由于极化选择性产生的极化信道之间的功率不平衡。从频域上看,去极化效应体现为极化状态的偏移和极化状态正交两分量的功率增益不平衡[27],分别称为极化模式色散(Polarization Mode Dispersion, PMD)和极化相关损耗(Polarization Dependent Loss, PDL)[28-29]。产生PDL的主要原因就是两路信号之间能量的耦合,PMD效应则用来说明这种耦合关于与频率之间的关系。
2.6 卫星双极化信道
在卫星通信系统中,采用虚拟极化技术实现收发任意极化状态,因此需要采用双正交抛物面极化天线(Orthogonal Dual Parabolic Polarized Antenna, ODPPAs)。
双极化窄带卫星通信信道基本模型如图4所示,可以等效成为一个隔离的2x2的MIMO (Multi-input Multi-output) :
(11)
式中,hXY为X极化发射天线与Y极化接收天线无线信道间的信道增益。将该信道进行奇异值分解,U和V为酉矩阵,λi(i=1,2)为信道的特征值。由于极化状态受酉矩阵的影响,极化基会发生变化,则U和V会造成极化状态的刚性旋转[29],但极化的相对位置以及功率都不会发生改变。
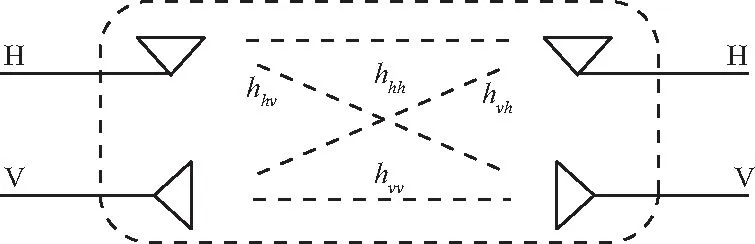
图4 双极化信道基本模型
因此,PDL效应可以定义为:
(12)
经过PDL效应影响之后,接收信号的特征有:
(13)
ρ=λ1cos2γy+λ2sin2γy,
(14)
式中,γz为接收到的极化角,ρ为相比于归一化接收到的功率,极化角辅角在传播过程中,一般不发生改变。
3 极化信息在卫星通信中发展趋势
信号极化特性在卫星通信系统中仍然存在如下一些问题值得进一步深入研究:
① 卫星通信被广泛应用于军事领域,而军用无线通信系统面临着严重的干扰,极化域抗干扰技术能够实现一定的增益。因此,在未来,在不同的干扰场景下,采取专门的极化域抗干扰技术将是研究重点。另外,利用斜投影滤波器在极化域实现抗干扰时,其中对干扰参数的识别至关紧要。目前对极化参数识别主要利用一些自适应滤波算法来估计,但是往往收敛速度不够快,在实际系统中是一个亟待解决的问题。因此,进一步探索极化参数的精确快速识别具有较高的研究价值。
② 在使用快速双极化变信号实现物理层安全传输时,自干扰的能量与原始信号的能量相同,因此在能耗方面并不可观,需要牺牲较多的能量。在接下来的研究中,可以根据实际的信道,对干扰信号能量进行优化,设计更加成熟的安全传输方案。
③ 卫星正朝着大容量、高带宽方向发展。如何从极化复用角度提高系统吞吐率以及提升高带宽的频谱利用率将是未来发展的一个重要方向。
4 结束语
首先结合当前极化信息理论和最新研究成果,从电磁波基本场的概念出发引出了极化表征的方法,阐述了极化与天线之间的关系,在此基础上,分析了任意极化状态的产生以及接收方法。进而,阐述了卫星通信双极化信道模型以及去极化效应对信号产生的影响,最后分析了极化特性在卫星通信中的发展趋势。卫星通信作为一种重要的通信方式,信号的极化特性丰富了传输理论,在极化领域进行进一步深入探究,能够缓解当前卫星通信系统中频谱资源紧张、能耗高、干扰严重等问题,可为未来卫星通信系统容量提升、能耗降低、干扰消除等热点问题开辟新的途径。
[1]易克初,李怡,孙晨华,等.卫星通信的近期发展与前景展望[J].通信学报,2015, 36(6): 157-172.
[2]Andrews M R, Mitra P P, Decarvalho R. Tripling the Capacity of Wireless Communications Using Electromagnetic Polarization[J].Nature,2001, 409(6818):316-324.
[3]Dietrich C B,Dietze K, Nealy J R, et al. Spatial, Polarization, and Pattern Diversity for Wireless Handheld Terminals [J].IEEE Transactions on Antennas & Propagation, 2001, 49(9): 1271-1281.
[4]Guo C, Liu F, Chen S, et al. Advances on Exploiting Polarization in Wireless Communi-cations: Channels, Technologies, and Applications[J]. IEEE Communications Surveys & Tutorials, 2016, PP(99):1-1.
[5]Guo C, Chen S, Liu F. Polarization-Based Spectrum Sensing Algorithms for Cognitive Radios: Upper and Practical Bounds and Experimental Assessment[J]. IEEE Transactions on Vehicular Technology, 2016, 65(10): 8072-8086.
[6]Boerner W M, Yan L. Basic Principles of Radar Polarimetry and Its Application to Target Recognition Problems with Ascendants of Historical Development and of the Current State-of-art [C]//Proceeding of the NATO Advanced Study Institute on Modeling and Measurements for Analysis of Synthesis Problems,1991:311-363.
[7]Thi T N,Hwang K C,Kim H B.Dual-band Circularly-polarized Spidron Fractal Micro Strip Patch Antenna for Ku-band Satellite Communication Applications[J]. Electrics Letters,2013, 49(7):444-445.
[8]Smolders A B,Mestrom R M C, Reniers A C F, et al. A Shared Aperture Dual-frequency Circularly Polarized Micro Strip Array Antenna[J]. IEEE Antennas and Wireless Propagation Letters, 2013, 12:120-123.
[9]Maitra A, Chakravarty K. RainDepolarization Measurements on Low Margin Ku-band Satellite Signal at a Tropical Location[J]. IEEE Antennas and Wireless Propagation Letters,2009, 8:445-448.
[10] Lee L S. PolarizationControl Schemes for Satellite Communications with Multiple Up-links[J]. IEEE Trans on Communication,1979, 27(10):1504-1512.
[11] Cuinas I, Sanchez M G, ALEJOS A V. Depolarization due to scattering on walls in the 5 GHz Band[J]. IEEE Antennas and Wireless Propagation Letters, 2009, 57(6):1804-1812.
[12] Zhang X,Zhang B,Guo D. Poly-polarization Multiplexing in Narrow-band Wireless Communication Aid By Multi-notch OPPFs and Optimal Pre-compensation [J].IEEE Wireless Communications Letters, 2017, 6(4):478-481.
[13] 张晓凯,张邦宁,郭道省,等.极化调制在卫星中的应用[J].微型机与应用,2017(11): 66-70.
[14] An K, Lin M, Ouyang J, et al. Secure Transmission in Cognitive Satellite Terrestrial Networks[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(11):3025-3037.
[15] Zhang X,Zhang B,Guo D.Physical Layer Secure Transmission Based on Fast Dual Polarization Hopping in Fixed Downlink Satcom [J].IEEE Access, 2017, 5:11782-11790.
[16] 庄钊文. 雷达极化信息处理及其应用[M].北京:国防工业出版社, 1999.
[17] Dietlein C, Luukanen A, Popovic Z, et al. A W-Band Polarization Converter and Isolator [J]. Antennas & Propagation IEEE Transactions on, 2007, 55(6):1804-1809.
[18] Doumanis E, Goussetis G, Dickie R, et al. Electronically Reconfigurable Liquid Crystal Based Mm-Wave Polarization Converter[J]. IEEE Transactions on Antennas & Propaga-tion, 2014, 62(4):2302-2307.
[19] Hallam B T, Lawrence C R, Hooper I R, et al. Broad-bandPolarization Conversion from a Finite Periodic Structure in the Microwave Regime[J]. Applied Physics Letters, 2004, 84(6):849-851.
[20] Zhong S S, Yang X X, Gao S C. Polarization-agile Microstrip Antenna Array Using a Sin-gle Phase-shift Circuit[J]. IEEE Transactions on Antennas & Propagation, 2004, 52(1):84-87.
[21] Fukusako T, Imahase A, Mita N. Polarization Characteristics of Patch Antenna Using in-plane and Weakly Biased Ferrite Substrate[J]. Antennas & Propagation IEEE Transactions on, 2004, 52(1):325-327.
[22] Xiao J J, Nehorai A. Optimal Polarized Beampattern Synthesis Using a Vector Antenna Ar-ray[J]. IEEE Transactions on Signal Processing, 2009, 57(2):576-587.
[23] Poelman A J. Virtual Polarization Adaptation-a Method of Increasing the Detection Capa-bility of a Radar System Through Polarization-vector Processing[J]. Communications, Radar and Signal Processing, IEE Proceedings F ,1981, 128(5):261-270.
[24] 伊波利托. 卫星通信系统工程[M]. 北京:国防工业出版社, 2012.
[25] Athanasiadou G E, Nix A R. A Novel 3-D Indoor Ray-tracing Propagation Model: the Path Generator and Evaluation of Narrow-band and Wide-band Predictions[J]. Vehicular Tech-nology IEEE Transactions on, 2000, 49(4):1152-1168.
[26] Kwon S C,Stuber G L. Geometrical Theory of Channel Depolarization[J]. IEEE Trans-actions on Vehicular Technology, 2011, 60(8):3542-3556.
[27] Nair L R,Maharaj B T. Comparative Model Analysis for a Dual-Polarized Indoor and Industrial MIMO System[C]//IEEE International Conference on Wireless and Mobile Computing, Networking and Communications. IEEE, 2009:7-12.
[28] Molisch A F, Asplund H, Heddergott R, et al. The COST259 Directional Channel Mod-el-Part I: Overview and Methodology[J]. IEEE Transactions on Wireless Communications, 2006, 5(12):3421-3433.
[29] Tenoux T, Lostanlen Y. Modeling and Analysis of the Radio Wave Depolarization in Urban Environments[J]. Physical Communication, 2012, 5(4):338-351.
[30] 代大海, 王雪松, 肖顺平,等. 电磁波极化变换的数学原理及其性质[J]. 中国科学:物理学 力学 天文学, 2008(10):1301-1311.

