基于混合变异的人工蜂群算法

张晓庆, 高 尚,范霁月

(江苏科技大学 计算机科学与工程学院, 镇江 212003)

人工蜂群算法(artificial bee colony algrithm,ABC)是文献[1]中提出的一种群智能优化算法,与其他智能优化算法相比,该算法具有控制参数少、鲁棒性强、易于实现等优点,已被成功应用于组合优化[2]、无线传感网络[3]、图像处理[4]等领域．然而,原始的人工蜂群算法存在局部搜索能力较差、收敛速度较慢以及易于陷入局部最优的缺点,为此,众多学者对其进行了大量的研究．文献[5-6]中利用混沌序列的随机性、遍历性和规律性,设计了一种混沌搜索算子,以提高算法的搜索精度和收敛速度;文献[7]中提出了一种新的选择策略和交叉策略以提高算法的收敛速度;文献[8]中将信息熵引入跟随蜂的选择策略中,避免了算法陷入局部最优值的问题,增加了全局搜索能力;文献[2]中利用全局最优解和个体极值改进了搜索模式,并引入异步变化学习因子以提高算法的局部搜索能力;文献[9]中提出一种基于文化算法的人工蜂群算法,利用信度空间中的规范知识调整搜索范围,提高了算法的收敛速度和勘探能力;文献[10]中提出了在差分变异算子中引入混沌序列以增强算法的局部搜索能力,并提高了其收敛速度和解的精度．

为了进一步提高人工蜂群算法的性能,文中利用差分进化算法和高斯变异算法在维护种群多样性以及搜索能力方面的较强优势,将混合变异算子引入到人工蜂群算法,并从两个方面对原始算法进行了改进．首先,跟随蜂采用了基于当前最优解的差分变异搜索策略在食物源附近进行搜索,利用差分变异的思想提高了算法的全局搜索能力,丰富了解的多样性,并通过当前最优解的引导,使算法的收敛速度加快;其次,当某个食物源位置长时间没有更新时,侦查蜂通过高斯变异局部最优解来生成新的食物源位置,避免了解的随机性,加快了算法的收敛速度．通过测试函数的仿真实验结果表明,文中提出的基于混合变异的人工蜂群算法有效提高了收敛速度和求解精度．

1 人工蜂群算法

人工蜂群算法的思想源于自然界中的蜜蜂采蜜行为,蜜蜂寻找优质食物源的过程可视为函数寻找最优解的过程．蜂群产生的智能群体模型中主要包括食物源、引领蜂、侦查蜂和跟随蜂4个部分,每个解代表一个食物源,解的个数等于引领蜂或跟随蜂的个数,引领蜂丢弃食物源之后转变为侦查蜂,食物源的花蜜丰富程度由适应度值来决定．

假设人工蜂群算法在D维搜索空间内随机产生SN个初始解(食物源),每个解可表示为xi=(xi1,xi2,…,xiD),i=1, 2,…,SN．首先,引领蜂在食物源附近(邻域内)进行循环搜索,以更新食物源的位置,其方式如下:

vij=xij+rij(xij-xkj)

(1)

式中：vij为候选食物源；xk为随机选取的一个已知解,j为解对应的维数,且有k不等于i；rij为用来控制xij位置处的邻域大小的随机参数,取值在[-1,1]内,随着迭代次数的增加,邻域的半径会逐渐缩小,最终获得最优解．

引领蜂在食物源的位置更新后,比较候选食物源与原始食物源的花蜜丰富程度,如果候选食物源的适应度值高于原始食物源,则用候选食物源代替原始食物源,否则保持原始食物源的位置不发生变化．然后,引领蜂返回到舞蹈区域,并通过摇摆舞方式将各个食物源的花蜜信息传递给跟随蜂,跟随蜂根据食物源的收益率来选择到哪个食物源进行采蜜行为．收益率与适应度值密切相关,食物源选择的概率如下:

(2)

(3)

式中：Pi为第i个食物源的选择概率；fiti为第i个食物源的适应度值；SN为食物源的个数；fi为优化问题的目标函数值．

由式(3)可知,当目标函数值fi≥0时,适应度值fiti随着目标函数值fi的减小而逐渐增大;当目标函数值fi<0时,适应度值fiti也随着目标函数值fi的减小而逐渐增大,又由式(2)可知,fiti越大,食物源的收益率越大,进而食物源被选择的概率越高．

跟随蜂在选中食物源之后,也根据式(1)在其邻域内进行搜索,并通过比较适应度值,保留较好的食物源．如果引领蜂在经过limit次循环后,食物源的位置仍未更新,则表明这个食物源位置已陷入局部最优,引领蜂应放弃该食物源,转变为侦查蜂,并随机生成一个新的食物源位置来代替原始的食物源位置,其方式:

xij=xminj+δ(xmaxj-xminj)

(4)

式中：xij为新的食物源i在第j维的分量,j∈{1,2,…,D}；xmin j为第j维分量的最小值；xmax j为第j维分量的最大值；δ为(0,1)范围内的随机数．

2 改进的人工蜂群算法

2.1 差分进化搜索策略

差分进化算法是文献[11]中提出的一种解决全局优化问题的方法．它是一种模拟生物进化的随机模型,通过不断迭代,使适应环境的个体被保留下来,引导搜索过程向最优解逼近．差分进化算法具有较强的全局收敛能力和鲁棒性,且进化过程中最核心的步骤为差分变异,其方式:

U=Xr1+F(Xr2-Xr3)

(5)

式中：U为变异后的个体；Xr1,Xr2,Xr3为随机选取的3个互不相同的个体；F为变异因子．

原始的人工蜂群算法中,跟随蜂和引领蜂采用相同的搜索策略,由式(1)可知,该搜索策略具有较好的全局搜索能力,而忽略了算法的局部搜索性能．为此,文献[12]中引入当前最优解,提出了一种新的搜索方式:

vij=xij+φij(xij-xkj)+φij(xbj-xij),

(6)

式中：vij为候选食物源；xk为随机选取的已知解；φij为[-1,1]上均匀分布的随机值；φij为[0,1.5]之间的随机值；xbj为当前最优的食物源位置．由式(6)可以看出,引入当前最优解后,算法的局部搜索能力在一定程度上得到了提高,加快了收敛速度．

为了进一步提高人工蜂群算法的全局搜索能力,增加种群的多样性,将差分进化算法中变异的思想引入到搜索策略中,即有:

vij=xij+η[(xpj-xqj)+(xbj-xij)]

(7)

且

(8)

式中：xpj,xqj为随机选取的两个已知解；xbj为当前最优的食物源位置；η为差分变异因子；itx为当前迭代的次数；MCN为最大迭代次数．

由式(8)可知,差分变异因子η随着迭代次数itx的增加而逐渐减小,又由式(7)可知,η越小,则蜂群搜查范围越小．在迭代初期,η较大,有利于扩大搜索空间,提高算法的全局搜索能力,增加解的多样性;而在迭代后期,η逐渐变小,有利于收敛到局部最优位置,从而提升收敛精度．

2.2 高斯变异侦查策略

高斯变异[12-13]是在原有个体的基础上添加一个服从高斯分布的随机扰动项,借助高斯随机扰动项,可以增强个体跳出局部最优解的能力,提高求解精度,其定义:

Xi=Xi+Xi·N(0,1)

(9)

式中：Xi为第i号个体；N(0, 1)为服从均值为0且方差为1的高斯分布．

原始的人工蜂群算法中,侦查蜂采用随机侦查策略,通过式(4)随机生成一个新的食物源来代替原始食物源,这样生成的食物源位置的随机性太强,导致收敛速度减慢,且易在搜索过程中陷入局部最优．因此,提出了一种更加有效的侦查策略,其方式:

(10)

与式(4)相比,式(10)利用高斯随机干扰项,让算法跳出当前最优值,变异生成一个新的食物源位置,使得侦查蜂在当前最优解附近进行局部搜索,基于当前最优解的高斯变异侦查策略可以有效避免解的随机性,加快收敛速度,提高解的精度．

2.3 基于混合变异的人工蜂群算法

在差分进化搜索策略和高斯变异侦察策略的基础上,基于混合变异算子的人工蜂群算法(artificial bee colony algrithm based on hybrid mutation operator,HMABC)的具体步骤:

(1) 随机生成SN个初始解,设置最大迭代次数MCN和limit值;

(2) 引领蜂根据式(1)在每个食物源的邻域内进行搜索,并计算新的食物源的适应度值,若新的食物源的适应度较大,则更新食物源的位置,否则,食物源位置不变;

(3) 找出当前的最优食物源xbj;

(4) 根据式(2)计算每个食物源被选择的概率,跟随蜂根据贪心搜索策略选择最优食物源,并根据式(7)进行局部搜索;

(5) 若食物源的位置在搜索次数达到limit次都没有更新,则放弃该食物源,引领蜂变成侦查蜂并根据式(10)在当前最优食物源附近产生一个新的食物源位置;

(6) 判断是否满足最大迭代次数,若不满足,则转入步骤(2),否则,输出最优位置．

3 实验分析

为了验证文中提出的HMABC算法的有效性,选择6种典型的测试函数进行仿真实验．将HMABC算法与原始的ABC算法、GABC算法[14]、ABCMSS算法[15]进行对比分析．表1给出了6种测试函数的表达式、搜索空间和最优值,其中f1(x)～f3(x)为单峰函数,用来测试算法的收敛速度和寻优精度;f4(x)～f6(x)为多峰函数,具有多个极值点,用来测试算法的全局寻优能力．

4种算法均采用随机生成初始解的方式,种群规模SN=100,搜索空间维数D=100,最大迭代次数MCN=1 000,limit=200．表2～7分别列出了4种算法对6种测试函数独立运行30次得到的实验结果．其中,均值反映了算法的平均精度,标准差反映了算法的稳定性．图1～6分别为测试函数的平均适应值进化曲线．

表1 测试函数

表2 Sphere函数上的实验对比

表3 Sum Squares函数上的实验对比

表4 Rosenbrock函数上的实验对比

表5 Rastrigin函数上的实验对比

表6 Ackley函数上的实验对比

表7 Griewank函数上的实验对比

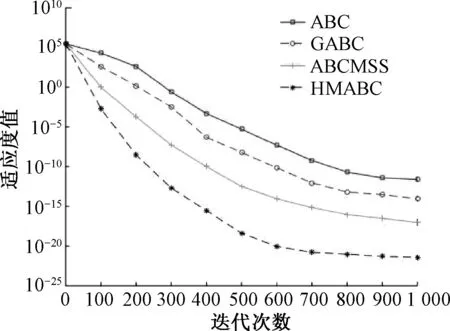
图1 Sphere函数进化曲线

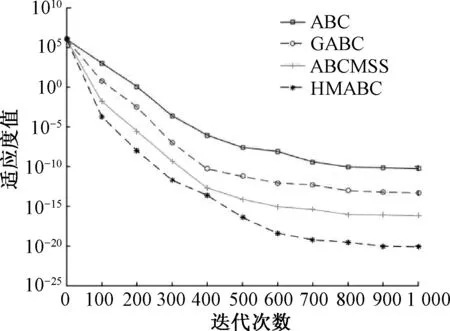
图2 Sum Squares函数进化曲线

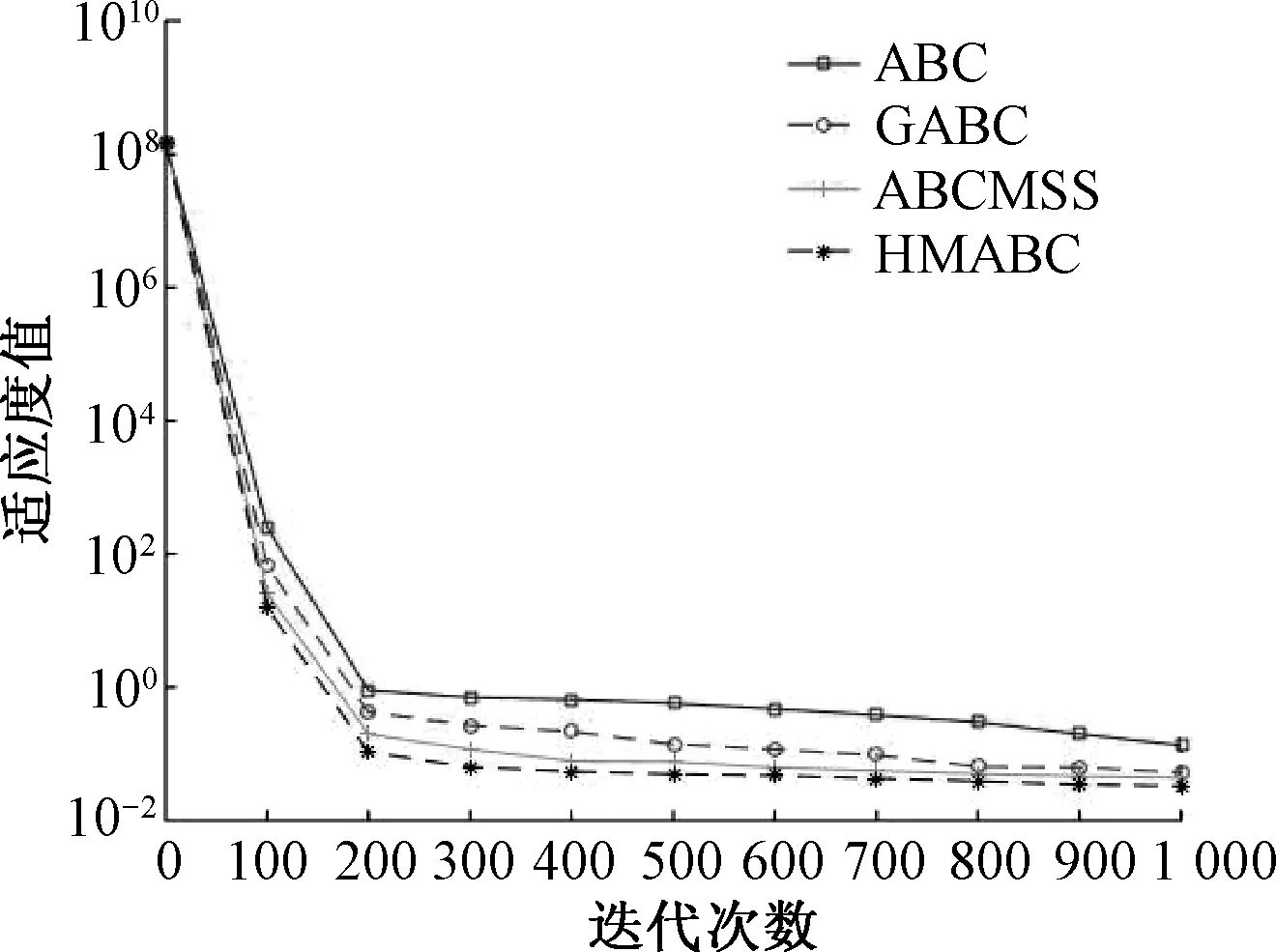
图3 Rosenbrock函数进化曲线

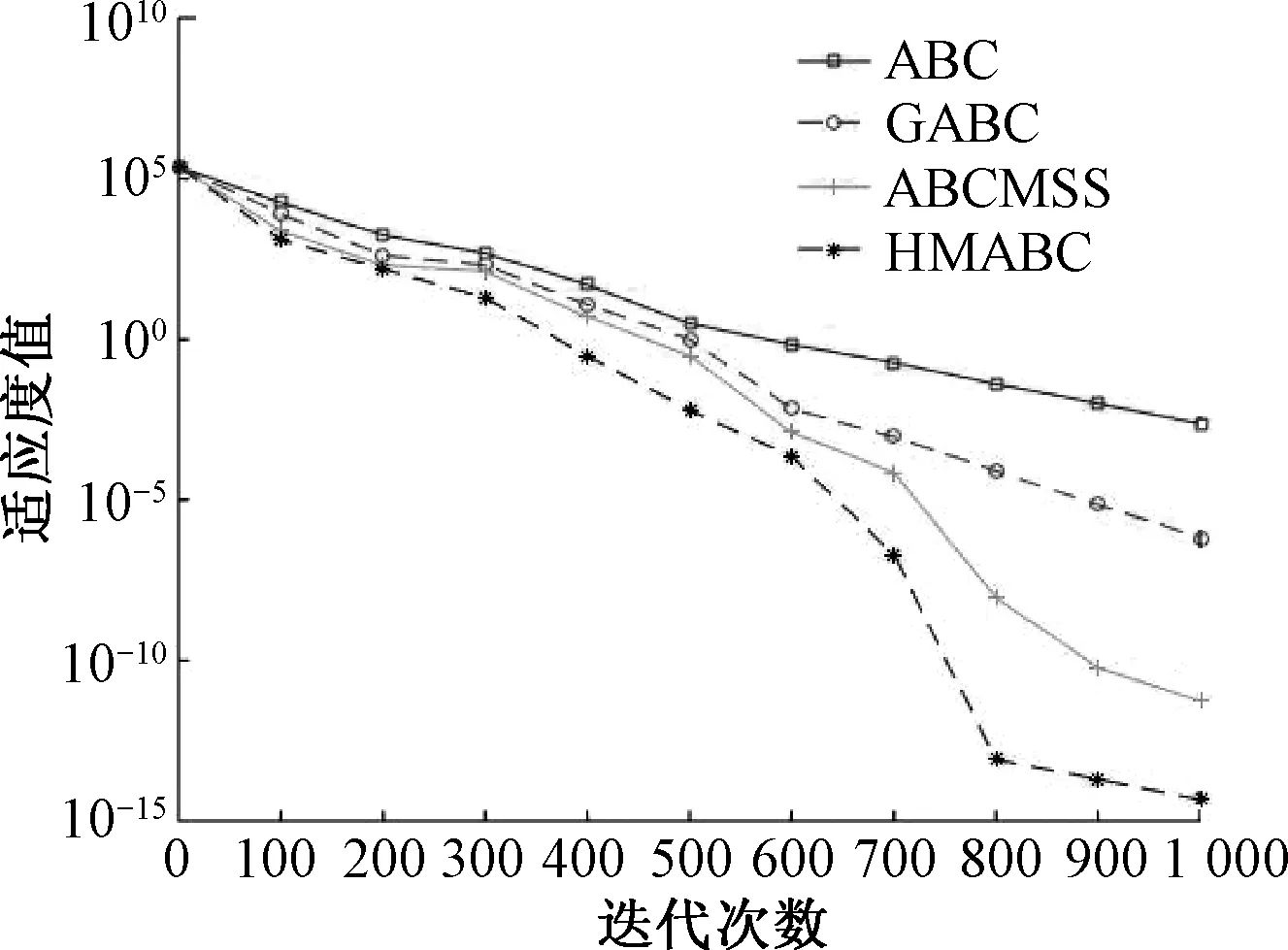
图4 Rastrigin函数进化曲线

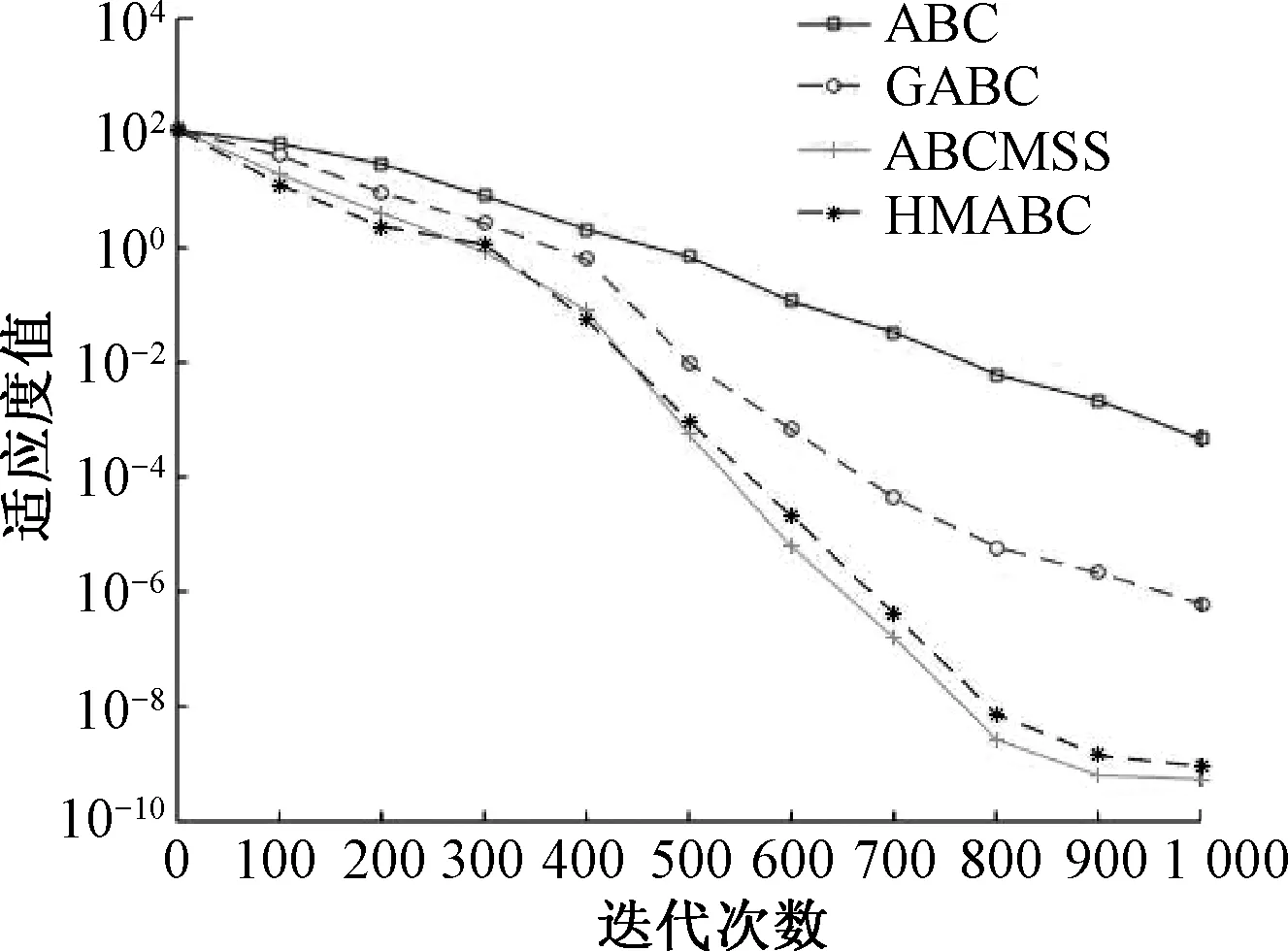
图5 Ackley函数进化曲线

图6 Griewank函数进化曲线

对于简单的单峰函数f1(x)～f2(x),从表2、3及图1、2可以看出，HMABC算法比ABC算法、GABC算法和ABCMSS算法具有更快的收敛速度和更高的寻优精度．对于比较复杂的单峰函数f3(x),在迭代初期,4种算法都具有较快的收敛速度,但由于其自身的特性,在迭代后期,算法的收敛速度减慢并容易陷入局部最优,而HMABC算法引入了混合变异的思想,能使其尽可能跳出局部最优值,提高了算法的收敛速度,从表4和图3也可以看出,HMABC算法的求解精度亦优于另外3种算法．

对于复杂的非线性多峰函数f4(x)～f6(x),从表5～7和图4～6可以看出,HMABC算法对于函数f5(x)的寻优结果略差于ABCMSS算法,但相比ABC算法和GABC算法仍有较为明显的优势,对于另外两种函数,HMABC算法的收敛速度和寻优精度都远优于ABC算法、GABC算法和ABCMSS算法．由于这3个函数本身的特性,传统的人工蜂群算法很容易陷入局部最优值,而HMABC算法引入差分变异的思想,增加了种群的多样性,平衡了算法的全局搜索能力和局部搜索能力,又引入高斯变异的思想,使其尽可能跳出局部最优值,提高了算法的寻优精度．由此可见,HMABC具有较强的全局搜索能力和较快的收敛速度．

4 结论

(1) 在传统的人工蜂群算法的基础上,针对算法局部搜索能力弱、收敛速度慢和易于陷入局部最优的缺陷,提出了一种基于当前最优解的差分进化搜索策略和高斯变异侦查策略的混合变异人工蜂群算法．

(2) 先通过差分变异因子在迭代初期进行全局搜索,增加解的多样性,在迭代后期进行局部搜索,提高了算法收敛速度,再通过高斯变异算子对侦查蜂的搜索模式进行改进,增强了算法的局部搜索能力,避免算法陷入局部最优．

(3) 6组基于典型的测试函数的实验结果表明,该算法的收敛速度和求解精度得到了显著提高．

References)

[1] KARABOGA D. An idea based on honey bee swarm for numerical optimization[R].[s.l.]:Erciyes University,2005.

[2] 王慧颖, 刘建军, 王全洲. 改进的人工蜂群算法在函数优化问题中的应用[J]. 计算机工程与应用, 2012, 48(19): 36-39. DOI:10.3778/j.issn.1002-8331.012.19.010.

WANG Huiying, LIU Jianjun, WANG Quanzhou. Modified artificial bee colony algorithm for numerical function optimization[J]. Computer Engineering and Applications, 2012, 48(19): 36-39. DOI:10.3778/j.issn.1002-8331.012.19.010.(in Chinese)

[3] 文政颖, 翟红生. 基于混沌人工蜂群算法的无线传感器网络覆盖优化[J]. 计算机测量与控制, 2014, 22(5): 1609-1612. DOI:10.3969/j.issn.1671-4598.014.05.092.

WEN Zhengying, ZHAI Hongsheng. Coverage optimization of wireless sensor networks base on chaotic artificial bee colony algorithm[J]. Computer Measurement & Control, 2014, 22(5): 1609-1612. DOI:10.3969/j.issn.1671-4598.014.05.092.(in Chinese)

[4] 梁建慧, 马苗. 人工蜂群算法在图像分割中的应用研究[J]. 计算机工程与应用, 2012, 48(8): 194-196,229. DOI:10.3778/j.issn.1002-8331.012.08.055.

LIANG Jianhui, MA Miao. Artificial bee colony algorithm based research on image segmentation[J]. Computer Engineering and Applications, 2012, 48(8): 194-196,229. DOI:10.3778/j.issn.1002-8331.012.08.055.(in Chinese)

[5] 王翔, 李志勇, 许国艺, 等. 基于混沌局部搜索算子的人工蜂群算法[J]. 计算机应用, 2012, 32(4): 1033-1036,1040. DOI:10.3724/SP.J.1087.012.01033.

WANG Xiang, LI Zhiyong, XU Guoyi, et al. Artificial bee colony algorithm based on chaos local search operator[J]. Journal of Computer Applications, 2012, 32(4): 1033-1036,1040. DOI:10.3724/SP.J.1087.012.01033.(in Chinese)

[6] 罗钧, 李研. 具有混沌搜索策略的蜂群优化算法[J]. 控制与决策, 2010, 25(12): 1913-1916.

LUO Jun, LI Yan. Artificial bee colony algorithm with chaotic-search strategy[J]. Control and Decision, 2010, 25(12): 1913-1916.(in Chinese)

[7] 毕晓君, 王艳娇. 加速收敛的人工蜂群算法[J]. 系统工程与电子技术, 2011, 33(12): 2755-2761. DOI:10.3969/j.issn.1001-506X.2011.12.34.

BI Xiaojun, WANG Yanjiao. Artificial bee colony algorithm with fast convergence[J]. Systems Engineering and Electronics, 2011, 33(12): 2755-2761. DOI:10.3969/j.issn.1001-506X.2011.12.34.(in Chinese)

[8] 李彦苍, 彭扬. 基于信息熵的改进人工蜂群算法[J]. 控制与决策, 2015, 30(6): 1121-1125. DOI:10.13195/j.kzyjc.2014.0377.

LI Yancang, PENG Yang. Improved artificial bee colony algorithm based on information entropy[J]. Control and Decision, 2015, 30(6): 1121-1125. DOI:10.13195/j.kzyjc.2014.0377.(in Chinese)

[9] 林小军, 叶东毅. 一种带规范知识引导的改进人工蜂群算法[J]. 模式识别与人工智能, 2013, 26(3): 307-314.

LIN Xiaojun, YE Dongyi. An improved artificial bee colony algorithm with guided normative knowledge[J]. Pattern Recognition and Artificial Intelligence, 2013, 26(3): 307-314.(in Chinese)

[10] 银建霞, 孟红云. 具有混沌差分进化搜索的人工蜂群算法[J]. 计算机工程与应用, 2011, 47(29): 27-30. DOI:10.3778/j.issn.1002-8331.011.9.008.

YIN Jianxia, MENG Hongyun. Artificial bee colony algorithm with chaotic differential evolution search[J]. Computer Engineering and Applications, 2011, 47(29): 27-30. DOI:10.3778/j.issn.1002-8331.011.9.008.(in Chinese)

[11] 杨启文, 蔡亮, 薛云灿. 差分进化算法综述[J]. 模式识别与人工智能, 2008, 21(4): 506-513. DOI:10.3969/j.issn.1003-6059.008.04.013.

YANG Qiwen, CAI Liang, XUE Yuncan. A survey of differential evolution algorithms[J]. Pattern Recognition and Artificial Intelligence, 2008, 21(4): 506-513. DOI:10.3969/j.issn.1003-6059.008.04.013.(in Chinese)

[12] 莫愿斌, 刘付永, 张宇楠. 带高斯变异的人工萤火虫优化算法[J]. 计算机应用研究, 2013, 30(1): 121-123. DOI:10.3969/j.issn.1001-3695.013.01.029.

MO Yuanbin, LIU Fuyong, ZHANG Yunan. Artificial glowworm swarm optimization algorithm with Gauss mutation[J]. Application Research of Computers, 2013, 30(1): 121-123. DOI:10.3969/j.issn.1001-3695.013.01.029.(in Chinese)

[13] 杨善友, 蓝新波. 融入变异算子的萤火虫算法[J]. 火力与指挥控制, 2014, 39(8): 47-50. DOI:10.3969/j.issn.1002-0640.014.08.012.

YANG Shanyou, LAN Xinbo. Growworm swarm optimization algorithm based on mutation operator[J]. Fire Control & Command Control, 2014, 39(8): 47-50. DOI:10.3969/j.issn.1002-0640.014.08.012.(in Chinese)

[14] ZHU G, KWONG S. Gbest-guided artificial bee colony algorithm for numerical function optimization[J]. Applied Mathematics and Computation, 2010, 217(7): 3166-3173. DOI:10.1016/j.amc.2010.08.049.

[15] 王志刚. 一种改进搜索策略的人工蜂群算法[J]. 计算机仿真, 2014, 31(10): 291-295. DOI:10.3969/j.issn.1006-9348.014.10.062.

WANG Zhigang. Artificial bee colony algorithm with modified search strategy[J]. Computer Simulation, 2014, 31(10): 291-295. DOI:10.3969/j.issn.1006-9348.014.10.062.(in Chinese)